Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(b)
I.
Question 1.
Write the following complex numbers in the form A + iB.
(i) (2 – 3i) (3 + 4i)
(ii) (1 + 2i)3
(iii) \(\frac{a-i b}{a+i b}\)
(iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)
(v) (-√3 + √-2) (2√3 – i)
(vi) (-5i) \(\left(\frac{i}{8}\right)\)
(vii) (-i) 2i
(viii) i9
(ix) i-19
(x) 3(7 + 7i) + i(7 + 7i)
(xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)
Solution:
(i) (2 – 3i) (3 + 4i) = 6 + 8i – 9i – 12i2
= 6 – i + 12
= 18 – i
= 18 + i(-1)
(ii) (1 + 2i)3 = 1 + 3 . i2 . 2i + 3 . 1 . 4i2 + 8i3
= 1 + 6i – 12 – 8i
= -11 – 2i
= (-11) + i(-2)


(v) (-√3 + √-2) (2√3 – i) = (-√3 + i√2) (2√3 – i)
= -6 + i√3 + i2√6 + √2
= (-6 + √2) + i(√3 + 2√6)
(vi) (-5i) \(\left(\frac{i}{8}\right)\) = \(\frac{-5 i^{2}}{8}\)
= \(\frac{5}{8}\) + i(0)
(vii) (-i)(2i) = -2i2
= -2(-1)
= 2
= 2 + i(0)
(viii) i9 = i4 . i4 . i
= 1 . 1 . i
= i
= 0 + i(1)
![]()
(ix) i-19 = \(\frac{1}{i^{19}}\)
= \(\frac{i}{i^{20}}\)
= \(\frac{i}{\left(i^{4}\right)^{5}}\)
= \(\frac{\mathrm{i}}{\mathrm{i}^{5}}\)
= i
= 0 + i(1)
(x) 3(7 + 7i) + i(7 + 7i)
= 21 + 21i + 7i – 7
= 14 + 28i

Question 2.
Write the conjugate of the following complex numbers.
(i) 3 + 4i
(ii) (15 + 3i) – (4 – 20i)
(iii) (2 + 5i) (-4 + 6i)
(iv) \(\frac{5 i}{7+i}\)
Solution:
(i) Let z = 3 + 4i
\(\bar{z}\) = 3 – 4i
(ii) Let z = (15 + 3i) – (4 – 20i)
= 15 + 3i – 4 + 20i
= 11 + 23i
\(\bar{z}\) = 11 – 23i
(iii) Let z = (2 + 5i) (-4 + 6i)
= -8 + 12i – 20i – 30
= -38 – 8i
\(\bar{z}\) = -38 + 8i

Question 3.
Simplify
(i) i2 + i4 + i6 + …….. + (2n + 1) terms
(ii) i18 – 3 . i7 + i2 (1 + i4) (-i)26
Solution:
(i) i2 + i4 + i6 + …….. + (2n + 1) terms
= -1 + 1 – 1 + (2n + 1) terms
= -1
(ii) i18 – 3i2 + i2 (1 + i4) (-i)26
= i16 . i2 – 3 . i4 . i3 + i2 (1 + 1) i24 . i2
= 1 . (-1) – 3 . 1 . (-i) + (-1) (2) (1) (-1)
= -1 + 3i + 2
= 1 + 3i
Question 4.
Find a square root for the following complex numbers.
(i) 7 + 24i
(ii) -8 – 6i
(iii) (3 + 4i)
(iv) (-47 + i8√3)
Solution:



![]()
Question 5.
Find the multiplicative inverse of the following complex numbers.
(i) √5 + 3i
(ii) -i
(iii) i-35
Solution:
(i) √5 + 3i
The multiplicative inverse of x + iy is \(\frac{x-i y}{x^{2}+y^{2}}\)

II.
Question 1.
(i) If (a + ib)2 = x + iy, find x2 + y2
Solution:
(a + ib)2 = x + iy
⇒ a2 + i(2ab) – b2 = x + iy
⇒ (a2 – b2) + i(2ab) = x + iy
⇒ (a2 – b2) + i(2ab) = x + iy
Equating real and imaginary parts on both sides, we have
x = a2 – b2 and y = 2ab
x2 + y2 = (a2 – b2)2 + (2ab)2
= a4 – 2a2b2 + b4 + 4a2b2
= a4 + 2a2b2 + b4
= (a2 + b2)2
(ii) If x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) then show that x2 + y2 = 4x – 3
Solution:
x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) \(\frac{(2+\cos \theta)-i \sin \theta}{(2+\cos \theta)-i \sin \theta}\)

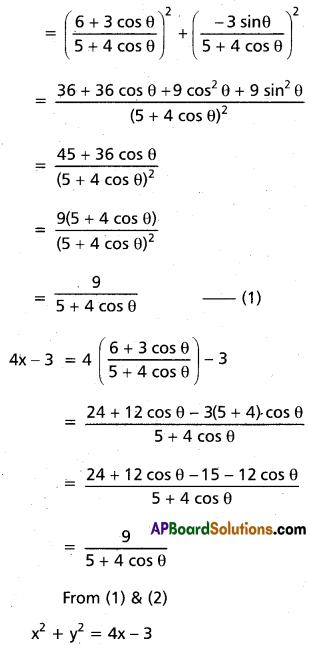
(iii) If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\), show that 4x2 – 1 = 0.
Solution:

Equating real parts on both sides, we have
x = \(\frac{1}{2}\)
⇒ 2x = 1
⇒ 4x2 = 1
⇒ 4x2 – 1= 0
(iv) If u + iv = \(\frac{2+i}{z+3}\) and z = x + iy, find u, v.
Solution:
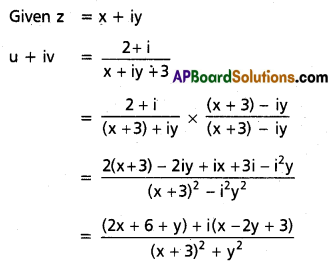
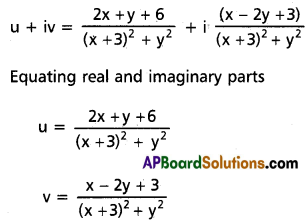
Question 2.
(i) If z = 3 – 5i Show that z3 – 10z2 + 58z – 136 = 0.
Solution:
Given z = 3 – 5i
⇒ z – 3 = -5i
⇒ (z – 3)2 = 25i2
⇒ z2 – 6z + 9 = -25
⇒ z2 – 6z + 34 = 0
∴ z3 – 10z2 + 58z – 136 = z(z2 – 6z + 34) – 4z2 + 24z – 136
= z(0) – 4(z2 – 6z + 34)
= 0 – 4(0)
= 0
∴ z3 – 10z2 + 58z – 136 = 0
![]()
(ii) If z = 2 – i√7 , then show that 3z3 – 4z2 + z + 88 = 0.
Solution:
Given z = 2 – i√7
⇒ z – 2 = -i√7
⇒ (z – 2)2 = (-i√7)2
⇒ z2 – 4z + 4 = 7i2
⇒ z2 – 4z + 4 = -7
⇒ z2 – 4z + 11 = 0
∴ 3z3 – 4z2 + z + 88 = 3z(z2 – 4z + 11) + 8z2 – 32z + 88
= 3z(0) + 8(z2 – 4z + 11)
= 0 + 8(0)
= 0
∴ 3z3 – 4z2 + z + 88 =0
(iii) Show that \(\frac{2-i}{(1-2 i)^{2}}\) and \(\left(\frac{-2-11 i}{25}\right)\) conjugate to each other.
Solution:

Question 3.
(i) If (x – iy)1/3 = a – ib then show that \(\frac{x}{a}+\frac{y}{b}\) = 4(a2 – b2)
Solution:
Given (x – iy)1/3 = (a – ib)
⇒ x – iy = (a – ib)3
⇒ x – iy = a3 – 3a2ib + 3ai2b2 – i3b3
⇒ x – iy = (a3 – 3ab2) – i(3a2b – b3)
Equating real and imaginary parts
x = a3 – 3ab2
⇒ \(\frac{x}{a}\) = a2 – 3b2
y = 3a2b – b3
⇒ \(\frac{y}{b}\) = 3a2 – b2
∴ \(\frac{x}{a}+\frac{y}{b}\) = a2 – 3b2 + 3a2 – b2
= 4a2 – 4b2
= 4(a2 – b2)
∴ \(\frac{x}{a}+\frac{y}{b}\) = 4(a2 – b2)
![]()
(ii) Write \(\left(\frac{a+i b}{a-i b}\right)^{2}-\left(\frac{a-i b}{a+i b}\right)^{2}\) in the form of x + iy.
Solution:

(iii) If x and y are real numbers such that \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-1}=i\), then determine the values of x and y.
Solution:
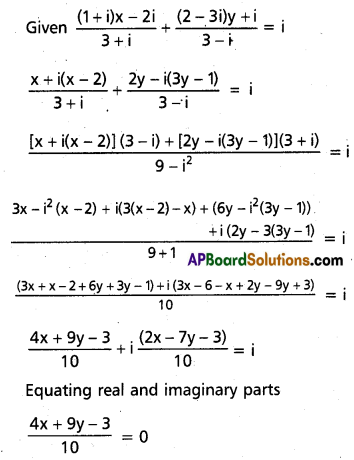

Question 4.
(i) Find the least positive integer n, satisfying \(\left(\frac{1+i}{1-i}\right)^{n}\) = 1
Solution:

(ii) If \(\left(\frac{1+i}{1-i}\right)^{3}-\left(\frac{1-i}{1+i}\right)^{3}\) = x + iy, find x and y.
Solution:

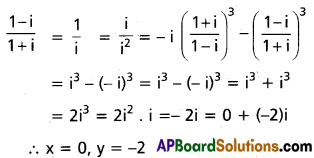
(iii) Find real values of ‘θ’ in order that \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) is a
(a) real numbers
(b) Purely imaginary number
Solution:

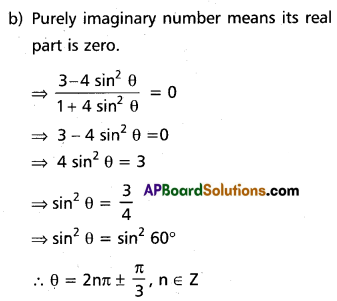
![]()
(iv) Find the real values of x and y if \(\frac{x-1}{3+i}+\frac{y-1}{3-i}=i\)
Solution:
Given \(\frac{x-1}{3+i}+\frac{y-1}{3-i}=i\)
⇒ \(\frac{(x-1)(3-i)+(y-1)(3+i)}{9-i^{2}}=i\)
⇒ 3x – xi – 3 + i + 3y – iy – 3 – i = 10i
⇒ (3x + 3y – 6) + i(-x + y) = 0 + 10i
Now equating real and imaginary parts
3x + 3y – 6 = 0
⇒ x + y – 2 = 0 ……..(1)
-x + y = 10
⇒ x – y + 10 = 0 ………(2)
(1) + (2) ⇒ 2x + 8 = 0
⇒ x = -4
From (1),
-4 + y – 2 = 0
⇒ y = 6
∴ x = -4, y = 6