Students get through Maths 1B Important Questions Inter 1st Year Maths 1B Applications of Derivatives Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B Applications of Derivatives Important Questions
Question 1.
Find dy and ∆y of y = f(x) = x2 + x at x = 10 when ∆x = 0.1.
Solution:
As change in y – f(x) is given by ∆y = f(x + ∆x) – f(x), this change at x = 10 with ∆x = 0.1 is
∆y = f(10.1) – f(10)
= {(10.1)2 + 10.1} – {102 + 10}
= 2.11.
Since dy = f'(x) ∆x, dy at x = 10 with ∆x = 0.1 is dy = {(2)(10) + 1} 0.1 = 2.1
(since \(\frac{\mathrm{d} y}{\mathrm{dx}}\) = 2x + 1).
![]()
Question 2.
Find ∆y and dy for the function y = cos (x) at x = 60° with ∆x = 1° .
Solution:
For the given problem ∆y and dy at x = 60° with ∆x = 1° are
∆y = cos (60° + 1°) – cos (60°) …………. (1)
and dy = -sin(60°) (1°) ………….. (2)
Cos (60°)= 0.5,
Cos (61°)= 0.4848,
Sin (60°) = 0.8660,
1° = 0.0174 radians
∴ ∆y = -0.0152 and
dy = -0.0150.
Question 3.
The side of a square is increased from 3 cm to 3.01 cm. Find the approximate increase in the area of the square.
Solution:
Let x be the side of a square and A be its area.
Then A = x2. …… (1)
Clearly A is a function of x. As the side is increased from 3 cm to 3.01 cm we can take x – 3 and ∆x = 0.01 to compute the approximate increase in the area of square. The approximate value of change in area is
∆A ≈ \(\frac{\mathrm{dA}}{\mathrm{dx}}\) ∆x
In view of equation (1), the equation (2) becomes
∆A ≈ 2x∆x
Hence the approximate increase in the area when the side is increased from 3 to 3.01 is
∆A ≈ 2(3)(0.01) = 0.06
Question 4.
If the radius of a sphere is increased from 7 cm to 7.02 cm then find the approximate increase in the volume of the sphere.
Solution:
Let r be the radius of a sphere and V be its volume. Then
V = \(\frac{4 \pi \pi^{2}}{3}\) …………….. (1)
Here V is a function of r. As the radius is increased from 7 cm to 7.02, we can take r = 7 cm and ∆r = 0.02 cm. Now we have to find the approximate increase in the volume of the sphere.
∴ ∆V ≈ \(\frac{\mathrm{dV}}{\mathrm{dr}}\) ∆r = 4πr2 ∆r.
Thus, the approximate increase in the volume of the sphere is \(\frac{4(22)(7)(7)(0.02)}{7}\) = 12.32 cm3.
![]()
Question 5.
If y = f(x) = k xn then show that the approximate relative error (or increase) in y is n times the relative error (or increase) in x where n and k are constants.
Solution:
The approximate relative error (or increase) in y by the equation (2) of if a number A is very close to a number B but it is not equal to B then A is called an approximate value of B is (\(\frac{f^{\prime}(x)}{f(x)}\)) ∆x = \(\frac{k n x^{n-1}}{k x^{n}}\) ∆x = n(\(\frac{\Delta x}{x}\) = n)
Hence the approximate relative error in y = kxn is n times the relative error in x.
Question 6.
If the increase in the side of a square is 2% then find the approximate percentage of increase in its area.
Solution:
Let x be the side of a square and A be its area.
Then A = x2.
Approximate percentage error in area A
= (\(\frac{\frac{\mathrm{dA}}{\mathrm{dx}}}{\mathrm{A}}\)) × 100 × ∆x(by (3) of if a number
A is very close to a number B but it is not equal to B then A is called an approximate value of B with f = A)
= \(\frac{100(2 x) \Delta x}{x^{2}}\) = \(\frac{200 \Delta x}{x}\) = 2(2) = 4
(∵ \(\frac{\Delta x}{x}\) × 100 = 2
Question 7.
If an error of 0.01 cm is made in measuring the perimeter of a circle and the perimeter is measured as 44 cm then find the approximate error and relative error in its area.
Solution:
Let r, p and A be the radius, perimeter and area of the circle respectively. Given that p = 44 cm and ∆p = 0.01. We have to find approximation of ∆A and \(\frac{\Delta \mathrm{A}}{\mathrm{A}}\). Note that A = πr2 which is a function of r. As p and ∆p are given we have to transform A = πr2 into the form A = f(p). This can be achieved by using the relation, perimeter 2πr = p.
∴ A = π(\(\frac{p}{2 \pi}\))2 = \(\frac{p^{2}}{4 \pi}\)
Hence the approximate error in
A = \(\frac{d A}{d p}\)∆p = \(\frac{2 p}{4 \pi}\)∆p = \(\frac{P}{2 \pi}\)∆p
The approximate error in A when p = 44 and ∆p = 0.01 = \(\) (0.01) = 0.07
The approximate relative error
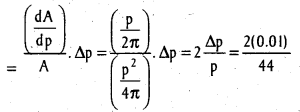
= 0.0004545.
![]()
Question 8.
Find the approximate value of \(\sqrt[3]{999}\)
Solution:
This problem can be answered by
f(x + ∆x) ≈ f(x) + f'(x) ∆x …………. (1)
with x = 1000 and ∆x = -1. The reason for taking x = 1000 is to make the calculation of f(x) simpler when f(x) = \(\sqrt[3]{x}\), Suppose
y = f(x) = \(\sqrt[3]{x}\)
The equation (1) becomes
f(x + ∆x) ≈ f(x) = \(\frac{1}{3 x^{\frac{2}{3}}}\) ∆x
Hence f(1000 – 1)
≈ f(1000) + \(\frac{1}{3(1000)^{2 / 3}}\) (-1) = 9.9967.
Question 9.
Find the slope of the tangent to the following curves at the points as indicated.
i) y = 5x2 at (-1, 5)
ii) y = \(\frac{1}{x – 1}\) (x ≠ 1) at [3, \(\frac{1}{2}\)]
iii) x = a secθ, y = a tanθ at θ = \(\frac{\pi}{6}\)
iv) (\(\frac{x}{a}\))n + (\(\frac{x}{b}\))n = 2 at (a, b)
Solution:
i) y = 5x2, then \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 10x
Slope of the tangent at the given points
(\(\frac{\mathrm{dy}}{\mathrm{dx}}\))(-1.5) -10(-1) = -10
ii) y = \(\frac{1}{x – 1}\)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{-1}{(x-1)^{2}}\)
Slope of the tangent at the given point is

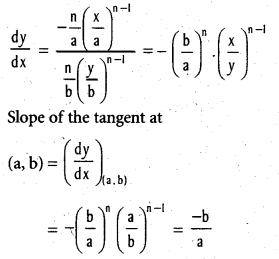
![]()
Question 10.
Find the equations of the tangent and the normal to the curve y = 5x4 at the point (1, 5)
Solution:
y = 5x4 implies that \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 20x3
Slope of the tangent to the curve at (1, 5) is
(\(\frac{\mathrm{dy}}{\mathrm{dx}}\))(1, 5) = 20(1)5 = 20
Equation of the normal of (1, 5) is
y – 5 = 20 (x – 1) = 20x – 20
y = 20x – 15
Slope of the normal to the curve at (1, 5) is
–\(\frac{1}{m}\) = –\(\frac{1}{20}\)
Equation of the normal of (1, 5) is
y – 5 = –\(\frac{1}{20}\) (x – 1)
20 y – 100 = -x + 1
x + 20y = 101
(or) 20y = 101 – x
Question 11.
Find the equations of the tangent and the normal to the curve y4 = ax3. at (a, a).
Solution:
Given curve is y4 = ax3
Differentiating w.r.to. x
4y3 . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 3ax2
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{3 a x^{2}}{4 y^{3}}\)
Slope of the tangent at (a, a) = \(\frac{3 a \cdot a^{2}}{4 a^{3}}\) = \(\frac{3}{4}\)
Slope of the normal at (a, a) = –\(\frac{1}{m}\) = –\(\frac{4}{3}\)
Equation of the tangent at (a, a) is
y – a = \(\frac{3}{4}\)(x – a)
4y – 4a = 3x – 3a
4y = 3x + a
Equation of the normal at (a, a) is 4
y – a = – \(\frac{4}{3}\)(x – a)
3y – 3a = -4x + 4a
3y + 4x = 7a
Question 12.
Find the equations of the tangent to the curve y = 3x2 – x3, where it meets the X-axis.
Solution:
Equation of the curve is y = 3x2 – x3
Equation of X – axis is y = 0
For points is intersection of the curve and X-axis
3x2 – x3 = 0 ⇒ x2 (3 – x) = 0
x = 0, x = 3
The curve crosses X-axis 0(0, 0) and A(3, 0)
y = -3x2 – x3
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 6x – 3x2
At O(0, 0), slope of the tangent = (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))(0, 0) = 0
Equation of the tangent at (0, 0) is y – 0, 0(x – 0) i.e., y = 0
i.e., x-axis is the tangent to the curve at O(0, 0)
At A(3, 0), slope of the tangent = (\(\frac{\mathrm{dy}}{\mathrm{dx}}\))(3, 0)
= 6.3 – 3.32
= 18 – 27
= -9
Equation of the tangent at A(3, 0) is
y – 0 = -9(x – 3) = -9x + 27
(or) 9x + y = 27
![]()
Question 13.
Find the points at which the curve t y = sin x has horizontal tangents.
Solution:
y = sin x
A tangent is horizontal if and anal its slope is
cos x = 0 ⇒ x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
Hence the given curve has horizontal tangents at points (x0, y0)
⇔ x0 = (2n + 1) . \(\frac{\pi}{2}\) and
y0 = (-1)n for same n ∈ Z
Question 14.
Verify whether the curve y = f(x) = x1/3 has a vertical tangent at the point with x = 0.
Solution:
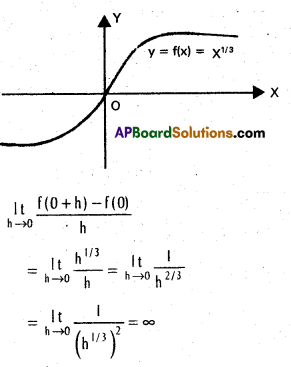
The function has a verified tangent at the point whose x co-ordinate is 0.
Question 15.
Find whether the curve y = f(x)= x2/3 has a vertical tangent at x = 0.
Solution:
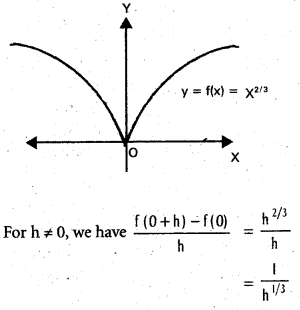
Thus left handed be normal \(\frac{1}{h^{1 / 3}}\) as h → 0 is -∞
While the right handed limit is ∞.
Hence 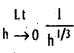 does not exist. The vertical tangent does not exist.
does not exist. The vertical tangent does not exist.
At the point x = 0.
![]()
Question 16.
Show that the tangent at any point 0 on the curve x = c sec θ, y = c tan θ is y sin θ = x – c cos θ.
Solution:
x = c sec θ, y = c tan θ
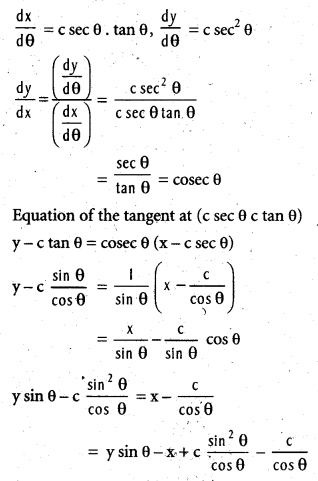
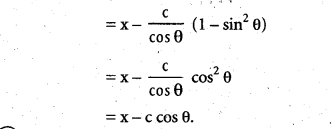
Question 17.
Show that the area of the triable formed by the tangent at any point on the curve xy = c (c ≠ 0) with the coordinate axis is constant.
Solution:
Observe that c ≠ 0
If c = 0 the equation xy = 0 represent the coordinate circle which is against the definite.
Let P (x1, y1) be a point on the curve xy = c
y = \(\frac{c}{x}\) = 1, \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = – \(\frac{c}{x^{2}}\)
Equation of the tangent at (x1, y1) is
y – y1 = – \(\frac{c}{x^{2}}\) (x – x1)
x2y – x12 = -cx + cx1
cx + x12 . y = x12 + cx1
= cx1 + cx1 (x1y1 = c)
= 2cx1
\(\frac{c x}{2 c x_{1}}\) + \(\frac{x_{1}^{2} y}{2 c x_{1}}\) = 1
\(\frac{x}{2 x_{1}}\) + \(\frac{y}{\left(\frac{2 c}{x_{1}}\right)}\) = 1
Area of the triangle formed with co-ordinate axes
= \(\frac{1}{2}\) |OA . OB|
= \(\frac{1}{2}\) (2x1) (\(\frac{2 c}{x_{1}}\)) = 2c = constant
![]()
Question 18.
Show that the equation of the tangent to the curve (\(\frac{x}{a}\))n + (\(\frac{y}{b}\))n = 2 (a ≠ 0, b ≠ 0) at the point (a, b) is \(\frac{x}{a}\) + \(\frac{y}{b}\) = 2
Solution:

Equation of the tangent to the curve at the point (a, b) is
y – b = \(\frac{-b}{a}\) (x – a)
\(\frac{y}{b}\) – 1 = – \(\frac{x}{a}\) + 1
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 2
Question 19.
Show that the length of the sub normal at point on the curve y2 = 4ax is a constant.
Solution:
Equation of the curve is y2 = 4ax
Differentiating w.r.to x
2y \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 4a
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{4a}{2y}\) = \(\frac{2a}{y}\)
Length of the sub-normal \(\left|\frac{y d y}{d x}\right|=\left|y \cdot \frac{2 a}{y}\right|\)
= 2a = constant
Question 20.
Show that the length of the Sub tangent at any point on the curve y = ax (a > 0) is a constant.
Solution:
Equation of the curve is y = ax
Differentiating w.r.to x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = ax log a = y. log a
Length of the sub-tangent
= \(\left|\frac{y}{\left(\frac{d y}{d x}\right)}\right|\) = \(\left|\frac{y}{\left(\frac{d y}{d x}\right)}\right|\) = \(\frac{1}{\log a}\) constant
![]()
Question 21.
Show that the square of the length of subtangent at any point on the curve by2 = (x + a)3 (b ≠ 0) varies with the length of the subnormal at that point.
Solution:
Differentiating by2 = (x + a)3
w.r.t x, we get
2by y’ = 3(x + a)2
∴ The length of the subnormal at any point (x, y) on the curve
= |y y’| = |\(\frac{3}{2 b}\)(x + a)2| ………………… (1)
The square of the length of subtangent
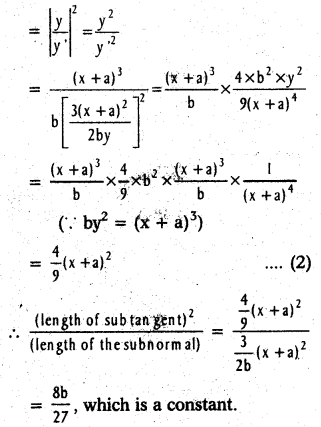
∴ (length of the subnormal)2 ∝ (length of subnormal).
Question 22.
Find the value of k, so that the length of the subnormal at any point on the curve y = a1 – kxk is a constant.
Solution:
Differentiating y = a1 – kxk with respect to x,
we get y’ = ka1 – kxk – 1
Length of subnormal at any point P(x, y) on the curve
= |y y’| = |yka1 – kxk – 1|
= |k a1 – kxka1 – kxk – 1|
= |ka2-2kx2k-1|
In order to make these values a constant, we should have 2k – 1 = 0 i.e., k = \(\frac{1}{2}\).
Question 23.
Find the angle between the curves xy = 2 and x2 + 4y = 0.
Solution:
First we find the points of intersection of xy = 2 and x2 + 4y = 0
y = \(\frac{-x^{2}}{4}\)
But xy = 2 ⇒ x(\(\frac{-x^{2}}{4}\)) = 2 ⇒ x3 = -8
x = -2
y = \(\frac{-x^{2}}{4}\) = – \(\frac{4}{4}\) = -1
Point of intersection is P(-2, -1)

= \(\left|\frac{-\frac{3}{2}}{\frac{1}{2}}\right|\) = 3
Φ = tan-1(3)
![]()
Question 24.
Find the angle between the curve 2y = e\(\frac{-x}{2}\) and Y-axis.
Solution:
Equation of Y-axis is x = 0.
The point of intersection of the curve
2y = e\(\frac{-x}{2}\) and x = 0 is P(0, \(\frac{1}{2}\))
Let ψ be the angle between the given curves
2y = e\(\frac{-x}{2}\) at P with X – axis is given by
tan ψ = \(\left.\frac{\mathrm{dy}}{\mathrm{dx}}\right|_{\left(0, \frac{1}{2}\right)}=\left.\frac{-1}{4} \mathrm{e}^{\frac{-x}{2}}\right|_{\left(0, \frac{1}{2}\right)}=\frac{-1}{4}\)
Further, if Φ is the angle between the Y – axis and 2y = e\(\frac{-x}{2}\), then we have
tan Φ = |tan (\(\frac{\pi}{2}\) – ψ)| = |cot ψ| = 4
∴ The angle between the curve and the Y-axis is tan-1 4.
Question 25.
Show that the condition of the orthogonality of the curves ax2 + by2 = 1 and a1x2 + b1y2 = 1 is \(\frac{1}{a}\) – \(\frac{1}{b}\) = \(\frac{1}{a_{1}}\) – \(\frac{1}{b_{1}}\).
Solution:
Let the curves ax2 + by2 = 1 and a1x2 + b1y2 = 1 intersect at p(x1, y1) so that
ax12 + by12 = 1 and a1x12 + b1y12 = 1, from which we get,
\(\frac{x_{1}^{2}}{b_{1}-b}\) = \(\frac{y_{1}^{2}}{a_{1}-a}\) = \(\frac{1}{a b_{1}-a_{1} b}\) …………. (1)
Differentiating ax2 + by2 = 1 with respect to x,
we get \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{-a x}{b y}\)
Hence, if mt is the slope of the tangent at P(x1, y1) to the curve
ax2 + by2 = 1, m1 = \(\frac{-a x_{1}}{b y_{1}}\)
Similarly, the slope (m2) of the tangent at P to
a1x2 + b1y2 = 1 is given by m2 = \(\frac{-a_{1} x_{1}}{b_{1} y_{1}}\)
Since the curves cut orthogonally we have m1m2 = -1,
i.e., \(\frac{\mathrm{a} a_{1} x_{1}^{2}}{\mathrm{~b} \mathrm{~b}_{1} y_{1}^{2}}\) = -1 or \(\frac{x_{1}^{2}}{y_{1}^{2}}=\frac{-b_{1}}{a a_{1}}\) ………………….. (2)
Now from (1) and (2), the condition for the orthogonality of the given curves is
\(\frac{b_{1}-b}{a-a_{1}}\) = \(\frac{b b_{1}}{a a_{1}}\)
or (b – a) a1b1 = (b1 – a1) ab
or \(\frac{1}{a}\) – \(\frac{1}{b}\) = \(\frac{1}{a_{1}}\) – \(\frac{1}{b_{1}}\)
Question 26.
Show that the curves y2 = 4(x + 1)and y2 = 36 (9 – x) intersect orthogonally. [Mar 11, May 06, 05]
Solution:
Solving y2 = 4(x + 1) and y2 = 36 (9 – x) for the points of intersection, we get
4(x + 1) = 36 (9 – x) 10x = 80 or x = 8
i.e., y2 = 4(x + 1) ⇒ y2 = 4(9) = 36 ⇒ y = ± 6
The points of intersection of the two curves are P(8, 6), Q(8, -6)
y2 = 4(x + 1) ⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{2}{y}\)
y2 = 36 (9 – x) ⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{-18}{y}\)
Slope of the tangent to the curve
y2 = 4(x + 1) at P is
m1 = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Slope of the tangent to the curve
y2 = 36 (9 – x) at P is
m2 = \(\frac{-18}{6}\) = -3
m1m2 = \(\frac{1}{3}\) × -3 = -1
⇒ the curves intersect orthogonally at P.
We can prove, similarly,that the curves intersect orthogonally at Q also.
![]()
Question 27.
Find the average rate of change of s = f (t) = 2t2 + 3 between t = 2 and t = 4.
Solution:
The average rate of change of s between t = 2 and t = 4 is \(\frac{f(4)-f(2)}{4-2}\) = \(\frac{35-11}{4-2}\) = 12.
Question 28.
Find the rate of change of area of a circle w.r.t. radius when r = 5 cm.
Solution:
Let A be the area of the circle with radius r.
Then A = πr2. Now, the rate of change of area A w.r.t. r is given by \(\frac{\mathrm{dA}}{\mathrm{dr}}\) = 2πr. When r = 5 cm.
\(\frac{\mathrm{dA}}{\mathrm{dr}}\) = 10 π.
Thus, the area of the circle is changing at the rate of 10 π cm2/cm.
Question 29.
The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of the edge is 10 centimeters ?
Solution:
Let x be the length of the edge of the cube, V be its volume and S be its surface area. Then, V = x3 and S = 6x2. Given that rate of change of volume is 9 cm3/sec.
Therefore, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 9 cm3/sec.
Now differentiating V w.r.t. t, we get,
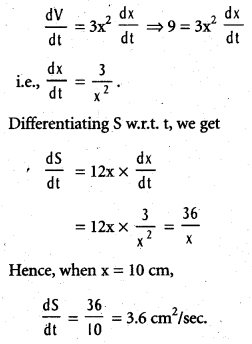
![]()
Question 30.
A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s = f(t) = 8t + t3. Find (i) the velocity at time t = 2 sec (ii) the initial velocity (iii) acceleration at t = 2 sec.
Solution:
The distance s and time t are connected by the relation.
s = f(t) = 8t + t3 …………. (1)
∴ velocity (ν) = 8 + 3t2 ……………. (2)
and the acceleration is given by
a = \(\frac{\mathrm{d}^{2} \mathrm{~s}}{\mathrm{dt}^{2}}\) = 6t
i) The velocity at
t = 2 is 8 + 3 (4) = 20cm/sec.
ii) The initial velocity (t = 0) is 8 cm/sec.
iii) The acceleration at t = 2 is 6(2) = 12 cm/sec2
Question 31.
A container in the shape of an inverted cone has height 12 cm and radius 6 cm at the top. If it is filled with water at the rate of 12 cm3/sec., what is the rate of change in the height of water level when the tank is filled 8 cm ?
Solution:
Let OC be height to water level at t sec. The triangles OAB ad OCD are similar triangles.
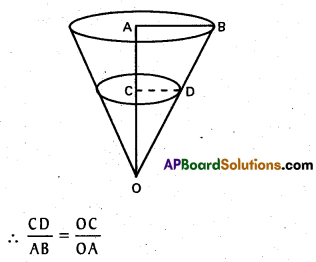
Let OC = h and CD = r. Given that AB = 6 cm, OA = 12 cm.
\(\frac{r}{6}\) = \(\frac{h}{12}\)

Hence, the rate of change of water level is \(\frac{3}{4 \pi}\) cm/sec when the water level of the tank is 8 cm.
Question 32.
A particle is moving along a line according to s = f (t) = 4t3 – 3t2 + 5t -1 where s is measured in meters and t is measured in seconds. Find the velocity and acceleration at time t. At what time ‘ the acceleration is zero.
Solution:
Since f(t) = 4t3 – 3t2 + 5t – 1, the velocity at time t is
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 12t2 – 6t + 5
and the acceleration at time t is a = \(\frac{\mathrm{d}^{2} \mathrm{~s}}{\mathrm{dt}^{2}}\) = 24t – 6.
The acceleration is 0 if 24t – 6 = 0
i.e., t = \(\frac{1}{4}\)
The acceleration of the particle is zero at
t = \(\frac{1}{4}\) sec.
![]()
Question 33.
The quantity (in mg) of a drug in the blood at time t (sec) is given by q = 3(0.4)t. Find the instantaneous rate of change at t = 2 sec.
Solution:
Given that q = 3(0.4)t
∴ \(\frac{\mathrm{dQ}}{\mathrm{dx}}\) = 3(0.4)t loge(0.4) is the instaneous rate of change in q. Hence the instaneous rate of q at time t = 2 sec. is given by
\(\left(\frac{\mathrm{dQ}}{\mathrm{dx}}\right)_{t=2}\) = 3(0.4)2 loge (0.4).
Question 34.
Let a kind of bacteria grow by t3 (t in sec). At what time the rate of growth of the bacteria is 300 bacteria per sec ?
Solution:
Let g be the amount of growth of bacteria at t sec. Then
g(t) = t3 ………… (1)
The growth rate at time t is given by
g'(t) = 3t2
300 = 3t2 (given that growth rate is 300)
t = 10 sec.
∴ After t = 10 sec, the growth rate of bacteria should be 300 bacteria/sec.
Question 35.
The total cost C(x) in rupees associated with production of x units of an item is given by C(x) = 0.005 x3 – 0.02x2 + 30x + 500. Find the marginal cost when 3 units are produced (marginal cost is the rate of change of total cost).
Solution:
Let M represent the marginal cost. Then
M = \(\frac{\mathrm{dC}}{\mathrm{dx}}\)
Hence,
M = \(\frac{\mathrm{d}}{\mathrm{dx}}\)(0.005x3 – 0.02x2 + 30x + 500) dx
= 0.005(3x2) – 0.02(2x) + 30
∴ The Marginal cost at x = 3 is
(M)x = 3 = 0.005 (27) – 0.02 (6) + 30 = 30.015.
Hence the required marginal cost is Rs. 30.02 to produce 3 units.
![]()
Question 36.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. Find the marginal revenue when x = 5 (marginal revenue is the rate of change of total revenue).
Solution:
Let m denote the marginal revenue. Then
m = \(\frac{\mathrm{dR}}{\mathrm{dx}}\) (since the total revenue is R(x))
Given that R(x) = 3x2 + 36x + 5
∴ m = 6x + 36
The marginal revenue at x = 5 is
[m = \(\frac{\mathrm{dR}}{\mathrm{dx}}\)]x = 5 = 30 + 36 = 66
Hence the required marginal revenue is Rs. 66.
Question 37.
Verify Rolle’s theorem for the function y = f(x) = x2 + 4 in [-3, 3].
Solution:
Here f(x) = x2 = 4. f is continuous on [-3, 3] as x2 + 4 is a polynomial which is continuous on any closed interval. Further f(3) = f(-3) = 13 and f is differentiable on [-3, 3].
∴ By Rolle’s theorem ∃ c ∈ (-3, 3) such that f'(c) = 0
The point c = 0 ∈ (-3, 3). Thus Rolle’s theorem is verified.
Question 38.
Verify Rolle’s theorem for the function f(x) = x(x + 3)e-x/2 in [-3, 0].
Solution:
Here f(-3) = 0 and f(0) = 0.
We have
f'(x) = \(\frac{\left(-x^{2}+x+6\right)}{2} e^{\frac{-x}{2}}\)
f'(x) = 0 ⇔ -x2 + x + 6 = 0 ⇔ x = -2 or 3. Of these two values -2 is in the open interval (-3, 0) which satisfies the conclusion of Rolle’s theorem.
Question 39.
Let f(x) = (x -1) (x – 2) (x – 3). Prove that there is more than one ‘c’ in (1, 3) such that f'(c) = 0. [Mar 13]
Solution:
Observe that f is continuous on (1, 3) differentiable in (1, 3) and f(1) = f(3) = 0.
f'(x) = (x – 1) (x – 2) + (x – 1) (x – 3) + (x – 2) (x – 3)
= 3x2 – 12x + 11
\(\frac{12 \pm \sqrt{144-132}}{6}\) = 2 ± \(\frac{1}{\sqrt{3}}\)
Both these roots lie in the open interval (1, 3) and are such that the derivative vanishes at these points.
![]()
Question 40.
On the curve y = x2, find a point at which the tangent is parallel to the chord joining (0, 0) and (1, 1).
Solution:
The slope of the chord is \(\frac{1-0}{1-0}\) = 1.
The derivative is \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2x.
We want x such that 2x = 1
i.e., x = \(\frac{1}{2}\)
we not that \(\frac{1}{2}\) is in the open interval (0, 1), as required in the Lagrange’s mean value theorem.
The corresponding point on the curve is (\(\frac{1}{2}\), \(\frac{1}{4}\)).
Question 41.
Show that f(x) = 8x + 2 is a strictly increasing function on R without using the graph of y = f(x).
Solution:
Let x1, x2 ∈ R with x1 < x2. Then 8x1 < 8x2. Adding 2 to both sides of this inequality, we have 8x1 + 2 < 8x2 + 2. i.e., f(x1) < f(x2).
Thus
x1 < x2 ⇒ f(x1) < f(x2) ∀ x1, x2 ∈ R.
Therefore, the given function f is strictly increasing on R.
Question 42.
Show that f (x) = ex is strictly increasing on R (without graph).
Solution:
Let x1, x2 ∈ R such that x1 < x2. we know that if a > b then ea > eb
∴ x1 < x2 ⇒ ex1 < ex2
i.e., f(x1) < f(x2).
Hence the given function f is a strictly increasing function.
Question 43.
Show that f(x) = – x + 2 is strictly decreasing on R.
Solution:
Let x1, x2 ∈ R x1 < x2.
Then x1 < x2
⇒ -x1 > -x2
⇒ -x1 + 2 > -x2 + 2
⇒ f(x1) > f(x2).
Therefore the given function f is strictly decreasing on R.
![]()
Question 44.
Find the intervals on which
f(x) = x2 – 3x + 8 is increasing or decreasing ?
Solution:
Given fucntion is f(x) = x2 – 3x + 8.
Differentiating it w.r.t. x, we get f'(x) = 2x – 3
f(x) = 0 for x = 3/2.

since f'(x) < 0 in (-∞, 3/2) the function f(x) is strictly decreasing on (-∞, \(\frac{3}{2}\)) Further since f'(x) > 0 in (\(\frac{3}{2}\), -∞), the function f(x) is a strictly increasing function (\(\frac{3}{2}\), -∞).
Question 45.
Show that f(x) = |x| is strictly decreasing on (-∞, 0) and strictly increasing on (0, ∞).
Solution:
The given function is f(x) = |x| i.e.,
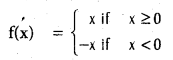
Thus f'(c) = 1 if c > 0, f'(c) = -1 if c < 0. Since f'(c) > 0 on (0, ∞), the function f(x) is strictly increasing on (0, ∞). Since f'(c) < 0 on (-∞, 0), the function f(x) is strictly decreasing on (-∞, 0).
Question 46.
Find the intervals on which the function f(x) = x3 + 5x2 – 8x + 1 is a strictly increasing function.
Solution:
Given that f(x) = x3 + 5x2 – 8x + 1.
∴ f'(x) = 3x2 + 10x – 8 = (3x – 2) (x + 4)
= 3(x – \(\frac{2}{3}\)) (x – (-4)).
f'(x) is negative in (-4, \(\frac{2}{3}\)) and positive in (-∞, -4) ∪ (\(\frac{2}{3}\), ∞) .
∴ The function is strictly deceasing in (-4, \(\frac{2}{3}\)) and is strictly decreasing in (-∞, -4)and (\(\frac{2}{3}\), ∞)
![]()
Question 47.
Find the Intervals on which f(x) = xx (x > 0) is increasing and decreasing.
Solution:
Taking logarithms on both sides of f(x) = xx
we get
log (f(x)) = x log x. Differenetiating it w.r.t. x
we have \(\frac{1}{f(x)}\) f'(x)= 1 + log x
∴ f'(x) = xx( 1 + log x)
f'(x) = 0 ⇒ xx(1 + log x) = 0 ……………. (1)
⇒ 1 + log x = 0
⇒ x = 1/e

Suppose x < 1/e log x < log (1/e) (since the base e > 1). i.e., log x < -1
1 + log x < 0 ⇒ xx (1 + log x) < 0. i.e., f'(x) < 0 Now suppose, x > 1/e. Then log x > log (1/e)
i.e., log x > – 1.
⇒ 1 + log x > 0
⇒ xx (1 + log x) > 0
⇒ f'(x) > 0
Hence, f is strictly decreasing on (o, 1/e) and it is strictly increasin on (1/e, ∞).
Question 48.
Determine the intervals in which f(x) = \(\frac{2}{(x-1)}\) + 18x ∀ x ∈ R \ {0} is strictly increasing and decreasing.
Solution:
Given that f(x) = \(\frac{2}{(x-1)}\) + 18x. Differenetiating
it w.r.t. x, we get
f'(x) = \(\frac{-1}{(x-1)^{2}}\) . 2 + 18 and f'(x) = 0
⇒ \(\frac{2}{(x-1)^{2}}\) = 18 ⇒ (x – 1)2 = 1/9.
∴ f'(x) = 0 if x – 1 = 1/3 or x- 1 = -(1/3).
i.e., x = 4/3 or x – 2/3.
The derivative of f(x) can be expressed as
f'(x) = \(\frac{18}{(x-1)^{2}}\) . (x – /3) (x – 4/3)

∴ The given function f(x) is strictly increasing on (-∞, \(\frac{2}{3}\)) and (\(\frac{4}{3}\), ∞) and it is strictly decreasing on (\(\frac{2}{3}\), \(\frac{4}{3}\)).
Question 49.
Let f(x) = sin x – cos x be defined on [0, 2π]. Determine the intervals in which f(x) is strictly decreasing and strictly increasing.
Solution:
Given that f(x) = sin x – cos x.
∴ f'(x) = cos x + sin x
∴ f'(x) = \(\sqrt{2}\) . sin(x + π/4)
Let 0 < x < 3π/4. Then π/4 < x + π/4 < π. ∴ sin (x + π/4) > 0 i.e., f'(x) > 0.
Similarly it can be shown that f'(x) < 0 in (3π/4 . 7π/4) and f'(x) > 0 in (7π/4, 2π).

Thus the function f(x) strictly increasing in (0, \(\frac{3\pi}{24}\) and (\(\frac{7\pi}{4}\), 2π) it is strictly decreasing in (\(\frac{3\pi}{4}\), \(\frac{7\pi}{4}\)).
![]()
Question 50.
If 0 ≤ x ≤ \(\frac{\pi}{2}\) then show that x ≥ sinx.
Solution:
Let f(x) = x – sin x. Then f'(x) = 1 – cos x ≥ 0 ∀ x
∴ f is an increasing function for all x.
Now, f(0) = 0. Hence f(x) ≥ f(0) for all x ∈ (0, \(\frac{\pi}{2}\)). Therefore, x ≥ in x.
Question 51.
Let f : R → R be defined by f(x) = 4x2 – 4x + 11. Find the global minimum value and a point of global minimum.
Solution:
We have to look for a value c e R(domain) such that
f(x) ≥ f(c) ∀ x ∈ R
so that f(c) is the global minimum value of f. Consider
f(x) = 4x2 – 4x + 11 = (2x – 1)2 + 10 ≥ ∀ x ∈ R ……………(1)
Now, f(1/2) = 10
Also f(x) ≥ f(1/2) ∀ x ∈ R
Hence, f(1/2) = 10 is the global minimum value of f(x), and a point of global minimum is x = 1/2.
Question 52.
Let f : [-2, 2] → R be defined by f(x) = |x|. Find the global maximum of f(x) and a point of global minimum.
Solution:
We know that |x| = \(\left\{\begin{array}{ccc}
x & \text { if } & x \geq 0 \\
-x & \text { if } & x<0
\end{array}\right.\)
Therefore, from the graph of the function f on [-2, 2] clearly f(x) ≤ f(2) and f(x) ≤ f(-2) ∀ x ∈ [-2, 2].
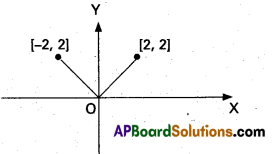
∴ f(2) = f(-2) = 2 is the global maximum of f(x), 2 and -2 are the points of global maximum.
Question 53.
Find the global maximum and global minimum of the function f : R → R defined by f (x) = x2.
Solution:
We have f(x) ≥ f(0) ∀ x ∈ R.
Hence th global minimum value of f(x) is 0 and a point of global minimum is x = 0.
Suppose f has global maximum at x0 ∈ R (x0 > 0). Then as per out assumption we have.
f(x0) ≥ f(x) ∀ x ∈ R
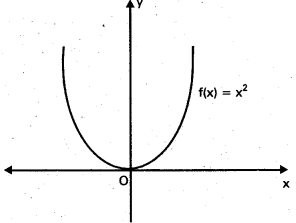
Choose x1 = x0 + 1. Then x1 ∈ R and x0 < x1
∴ x02 < x12
Hence f(x0) < (fx1)
Thus we got f(x1) such that f(x0) > f(x0) which is a contradition to Therefore, f(x) has no global maximum on R.
![]()
Question 54.
Find the stationary points of f(x) = 3x4 – 4x3 + 1, ∀ x ∈ R and state whether the function has local maxima or local minima at those points.
Solution:
Given that f(x) = 3x4 – 4x3 +1 and the domain of f is R. Differentiating the function w.r.t. x we have
f'(x) = 12x2(x – 1) ……………………… (1)
The stationary points are the roots of f (x) = 0 i.e., 12x2(x – 1) = 0. Hence x = 0 and x = 1 are the stationary points. Now, we test whether the stationary point x = 1 is a local extreme point or not. For.
f'(0.9) = 12(0.9)2 (0.9 – 1) ⇒ f'(0.9) is negative
f'(1.1) = 12(1.1)2 (1.1 – 1) ⇒ f'(1.1) is positive
and f(x) is defined in the neighbourhood i.e., (0.8, 1.2) of x = 1 with 8 = 0.2.
By theorem cis a point of local maximum if f(x) changes sign from positive to negative at x = c.
c is a point of local minimum if f'(x) changes sign from negative to positive at x = c.
The given function has local (relative) minimum at x = 1. Hence x = 1 is a local extreme point.
We will now test whether x = 0 is a local extreme point or not.
The function f(x) is defined in the neighbourhood of (-0.2, 0.2).
f'(-0.1) = 12(-0.1)2 (-0.1 – 1) ⇒ f'(-0.1) is negative
f'(-0.1) = 12(0.1)2 (0.1 -1) ⇒ f'(0.1) is negative
Thus, f(x) has no change in sign at x = 0. Therefore, the function f has no local maximum and no local minimum. Hence, x = 0 is not a local extreme point.
Question 55.
Find the points (if any) of local maxima and local minima of the function f (x) = x3 – 6x2 + 12x – 8 ∀ x ∈ R.
Solution:
Given function is f(x) = x3 – 6x2 + 12x – 8 and the domain of f is R.
Differentiating the given function w.r.t. x, we get
f'(x) = 3x2 – 12x + 12 i.e., f'(x) = 3(x – 2)2.
The stationary point of f(x) is x = 2, since 2 is a root of f'(x) = 0.
Choose δ = 0.2 The 0.2- neighbourhood of 2 is (1.8, 2.2). Now
f'(1.9) = 3(1.9 – 2)2 ⇒ f'(1.9) is positive
f'(2.1) = 3(2.1- 2)2 ⇒ f'(2.1) is positive
Thus f(x) does not change the sign at x = 2. By Theorem c is neither a point of local maximum nor a point of local minimum if f'(x) does not change sign at x = c.
x = 2 is neithere a local maximum nor a local minimum.
![]()
Question 56.
Find the points of local minimum and local maximum of the function f(x) = sin 2x ∀ x ∈ [0, 2π]
Solution:
The given function is f(x) = sin 2x and domain is [0, 2π].
f'(x) = 2cos 2x …………… (1)
The critical points are the roots of 2 cos 2x = 0 and lying in the domain [0, 2π].
They are \(\frac{\pi}{4}\) and \(\frac{3\pi}{4}\) .
Now we apply the first derivative test at x = \(\frac{\pi}{4}\)
Clearly (\(\frac{\pi}{4}\) – 0.1 . \(\frac{\pi}{4}\) + 0.1) is a neighbourhood of \(\frac{\pi}{4}\) and the given f is defined on it.
Now
f'(\(\frac{\pi}{4}\) – 0.05) = 2 cos(\(\frac{\pi}{2}\) – 0.1) > 0
f'(\(\frac{\pi}{4}\) + 0.05) = 2 cos(\(\frac{\pi}{2}\) + 0.1) < 0
Thus f'(x) changes sign from positive to negative at x = \(\frac{\pi}{4}\). Therefore f has a local maximum.
Now we apply the first derivative test at x = \(\frac{3\pi}{4}\).
Clearly (\(\frac{3\pi}{4}\) – 0.1 . \(\frac{3\pi}{4}\) + 0.1) is a neighbourhood of \(\frac{3\pi}{4}\) and the given f is defined on it.
Now
f'(\(\frac{3\pi}{4}\) – 0.05) = 2 cos(\(\frac{3\pi}{4}\) – 0.1) < 0 f'(\(\frac{3\pi}{4}\) + 0.05) = 2 cos(\(\frac{3\pi}{4}\) + 0.1) > 0
Thus f'(x) changes sign from positive to negative at x = \(\frac{3\pi}{4}\). Therefore f has a local maximum at x = \(\frac{3\pi}{4}\).
Question 57.
Find the points of local extrema of the function f(x) = x3 – 9x2 – 48x + 6 ∀ x ∈ R Also find its local extrema.
Solution:
Given function is
f(x) = x3 – 9x2 – 48x + 6 …………… (1)
and the domain of the function is R.
Differentiating (1) w.r.t. x we get
f'(x) = 3x2 – 18x – 48 = 3(x – 8) (x + 2) ………….. (2)
Thus the stationary points are – 2 and 8.
Differentiating (2) w.r.t.x we get,
f'(x) = 6(x – 3) ………….. (3)
Let x1 = -2 and x2 = 8. Now we have to find f’ at each of these points to know the sign of second derivative.
At x1 = -2, f'(-2) = – 30. The sign of it is negative.
∴ x1 = – 2 is a point of local maximum of f and its local maximum value is f(-2) – 58.
Now, at x2 = 8 f'(8) = 30. Thus the sign of f”(x2) is positive. Therefore, x = 8 is a point of local minimum of f and its local minimum value is
f(8) = – 442.
![]()
Question 58.
Find the points of local extrema of f(x) = x6 ∀ x ∈ R. Also find its local extrema.
Solution:
f(x) = x6 ………………….. (1)
Differentiating (1) w.r.t. x we get,
f'(x) = 6x5 ……………. (2)
and again differentiating (2) w.r.t. x we get
f'(x) = 30x4 …………………… (3)
The stationary point of f(x) is x = 0 only (since f'(x) = 0 only at x = 0).
Now f'(0) = 0. At x = 0, we can not conclude anything about the local extrema by the second derivative test. Therefore, we apply the first derivative test. As the domain of f is R, the function f is defined on (-0.2, 0.2) which is a neighbourhood of x = 0. Now
f'(-0.1) = 6(-0.1)5 < 0, f'(0, 1) = 6(0.1) 5 > 0.
Thus f'(x) changes sign form negative of positive at x = 0.
∴ x = 0 is a point of local minimum and its local minimum value is f(0) = 0.
Question 59.
Find the points of local extrema and local extrema for the function f(x) = cos 4x defined on (0, \(\frac{\pi}{2}\))
Solution:
Here f(x) = cos 4x ……………. (1)
and its domain is (0, \(\frac{\pi}{2}\))
∴ f’(x) = -4 sin 4x ………….. (2)
and f”(x) = -16 cos 4x ……………… (3)
The stationary points are the roots of
f'(x) = 0 and lying in the domain (o, \(\frac{\pi}{2}\)).
f'(x) = 0 ⇒ 4 sin 4x = 0
⇒ 4x = 0, π, 2π, 3π, 4π ………………….
⇒ x = 0, π/4, π/2, 3π/4, π …………………..
The point lying in the domain is x = \(\frac{\pi}{4}\) only.
Thus x = \(\frac{\pi}{4}\) is the stationary point of the given function. Now
f”(\(\frac{\pi}{4}\)) = -16 cos(π) = 16 > 0.
The function f has local minimum at x = \(\frac{\pi}{4}\) and its local minimum value is
f(\(\frac{\pi}{4}\)) = -1.
Question 60.
Find two positive number whose sum is 15 so that the sum of their squares is minimum.
Solution:
Suppose one numbers is x and the other number 15 – x. Let S be the sum of squares of these numbers. Then S = x2 + (15 – x)2 ………………… (1)
Note that the quantity S, to be minimized, is a function of x.
Differentiating (1) w.r.t. x, we get
\(\frac{\mathrm{dS}}{\mathrm{dx}}\) = 2x + 2(15 – x) (-1)
= 4x – 30 ………………. (2)
and again differentiating (2) w.r.t.x, we get
\(\frac{\mathrm{d}^{2} \mathrm{~S}}{\mathrm{dx}^{2}}\) = 4 ……………….. (3)
The stationary point can be obtained by solving \(\frac{\mathrm{dS}}{\mathrm{dx}}\) = 0 i.e., 4x – 30 = 0.
∴ x = 15/2 is the stationary point of (1).
Since \(\frac{\mathrm{d}^{2} \mathrm{~S}}{\mathrm{dx}^{2}}\) = 4 > 0, S is minimum at x = \(\frac{15}{2}\)
∴ The two numbers are \(\frac{15}{2}\), 15 – \(\frac{15}{2}\) i.e., \(\frac{15}{2}\) and \(\frac{15}{2}\).
![]()
Question 61.
Find the maximum area of the rectangle that can be formed with fixed perimeter 20.
Solution:
Let x and y denote the length and the breadth of a rectangle respectively. Given that the perimeter of the rectangle is 20.
i.e., 2(x + y) = 20
i.e., x + y = 10 ……………. (1)
Let A denote the area of rectangle.
Then A = xy ………….. (2)
Which is to be minimized. Equation (1) can be expressed as
y = 10 – x …………… (3)
From (3) and (2), we have
A = x (10 – x)
A = 10x – x2 ……………… (4)
Differentiating (4) w.r.t. x we get
\(\frac{\mathrm{dA}}{\mathrm{dx}}\) = 10 – 2x ……………….. (5)
The stationary point is a root of 10 – 2x = 0
∴ x = 5 is the stationary point.
Differentiating (5) w.r.t. x, we get
\(\frac{\mathrm{d}^{2} \mathrm{~A}}{\mathrm{dx}^{2}}\) = -2
which is negative. Therefore by second derivative test the area A is maximized at x = 5 and hence y = 10 – 5 = 5, and the maximum area is A = 5(5) = 25.
Question 62.
Find the point on the graph y2 = x which is the nearest to the point (4, 0).
Solution:
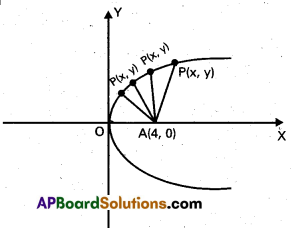
Let P(x, y) be any point on y2 = x and A(4, 0). We have to find P such that PA is minimum
Suppose PA = D. The quantity to be minimized is D.
D = (\(\sqrt{(x-4)^{2}+(y-0)^{2}}\)) ………………. (1)
P(x, y) lies on the curve, therefore
y2 = x …………………… (2)
From (1) and (2), we have
D = \(\sqrt{\left((x-4)^{2}+x\right)}\)
D = \(\sqrt{\left(x^{2}-7 x+16\right)}\) ……………………. (3)
Differentiating (3) w.r.t. x, we get
\(\frac{\mathrm{dD}}{\mathrm{dx}}\) = \(=\frac{2 x-7}{2} \cdot \frac{1}{\sqrt{x^{2}-7 x+16}}\)
Now \(\frac{\mathrm{dD}}{\mathrm{dx}}\) = 0
gives x = \(\frac{7}{2}\). Thus \(\frac{7}{2}\) is a stationary point of the function D. We apply the first derivative test to verify whether D is minimum at x = \(\frac{1}{2}\)

![]()
Question 63.
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
Solution:
Let O be the centre of the circular base of the cone and its height be h. Let r be the radius of the circular base of the cone.
Then AO = h, OC = r.
Let a cylinder with radius x(OE) be inscribed in the given cone. Let its height be u.
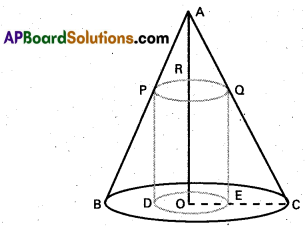
i.e., RO = QE = PD = u
Now the triangles AOC and QEC are similar.
Therefore,
\(\frac{\mathrm{QE}}{\mathrm{OA}}\) = \(\frac{\mathrm{EC}}{\mathrm{OC}}\)
i.e., \(\frac{u}{h}\) = \(\frac{r-x}{r}\)
∴ u = \(\frac{h(r-x)}{r}\) ………………… (1)
Let S denote the curved surface area of the chosen cylinder.Then
S = 2 π xu.
As the cone is fixed one, the values of r and h are constants. Thus S is function of x only. Now,
\(\frac{\mathrm{dS}}{\mathrm{dx}}\) = 2 πh (r – 2x)/r and \(\frac{\mathrm{d}^{2} \mathrm{~S}}{\mathrm{dx}^{2}}\) = -4πh/r.
The stationary point of S is a root of
\(\frac{\mathrm{dS}}{\mathrm{dx}}\) = 0
i.e., π(r – 2x)/r = 0
i.e., x = r/2
\(\frac{\mathrm{d}^{2} \mathrm{~S}}{\mathrm{dx}^{2}}\) < 0 for all x, Therefore (\(\frac{\mathrm{d}^{2} \mathrm{~S}}{\mathrm{dx}^{2}}\))x=r/2 < 0.
Hence, the radius of the cylinder of greatest curved surface area which can be inscribed in a given cone is r/2.
Question 64.
The profit function P(x) of a company, selling x items per day is given by P(x) = (150 – x)x – 1600. Find the number of items that the company should sell to get maximum profit. Also find the maximum profit.
Solution:
Given that the profit function is
P(x) = ( 150 – x)x – 1600 ………….. (1)
For maxima or minima \(\frac{\mathrm{dP}(\mathrm{x})}{\mathrm{dx}}\) = 0
∴ (150 – x) (1) + x (-1) = 0
i.e., x = 75
Now \(\frac{d^{2} P(x)}{d x^{2}}\) = -2 and \(\left[\frac{d^{2} P(x)}{d x^{2}}\right]_{x=75}\) < 0.
∴ The profit P(x) is maximum for x = 75.
∴ The company should sell 75 items a day to make maximum profit.
The maximum profit will be P(75) = 4025.
Question 65.
A manufacturer can sell x items at a price of rupees (5 – x/100) each. The cost price of x items is Rs. (x/5 + 500). Find the number of items that the manufacturer should sell to earn maximum profits.
Solution:
Let S(x) be the selling price of x items and C(x) be the cost price of x items. Then, we have
S(x) = {cost of each item}, x .
∴ S(x) = (5 – x/100) x = 5x – x2/100 and C(x) = x/5 + 500
Let P(x) denote the profit function. Then
P(x) = S(x) – C(x)
P(x) = (5x – x2/100) – (x/5 + 500)
– (24x/5) – (x2/100) – 500 …………….. (1)
For maxima or minima
\(\frac{\mathrm{dP}(\mathrm{x})}{\mathrm{d} x}\) = 0
i.e., 24/5 – x/50 = 0
The stationary point of P(x) is x = 240 and
\(\left[\frac{d^{2} P(x)}{d x^{2}}\right]\) = –\(\frac{1}{50}\) for all x.
Hence the manufacturer can earn maximum profit if he sells 240 items.
![]()
Question 66.
Find the absolute extrement of f(x) = x2 defined on [-2, 2].
Solution:
The given function f(x) = x2 is continuous on [-2, 2]. It can be shown that it has only local minimum and the point of local minimum is 0. The absolute(global) maximum of f is the largest value of f(-2), f(0) and f(2) i.e., 4, 0, 4.
Hence, the absolute maximum value is 4. Similarly the absolute minimum is the least value of 4, 0, 4. Hence 0 is the absolute minimum value.
Question 67.
Find the absolute maximum of x40 – x20 on the interval [0, 1]. Find also its absolute maximum value.
Solution:
Let f(x) = x40 – x20 ∀ x ∈ [0,1] ………… (1)
The function f is continuous on [0,1 j and the interval [0,1] is closed.
From (1) we have
f'(x) = 40 x39 – 20 x19 = 20x19 (2x20 – 1).
Thus f'(x) = 0 at x = 0 or
x = \(\left(\frac{1}{2}\right)^{\frac{1}{20}}\)
Therefore, the critical points of f are and \(\left(\frac{1}{2}\right)^{\frac{1}{20}}\) and 0 is one of the end points of the domain. Therefore no local maximum exists at x = 0. Now
f'(x) = 40(39) x38 – 20(19) x18
= 20x18 (78 x20 – 19)
[f”(x)]x = \(\left(\frac{1}{2}\right)^{\frac{1}{20}}\) = 20 (1/2)(18/20)[39 – 19] > 0.
Therefore f has local minimum at
x = (1/2)(1/20)
and its value is \(f\left(\left(\frac{1}{2}\right)^{\frac{1}{20}}\right)\) = –\(\frac{1}{4}\)
Therefore the absolute maximum value of the function f is the largest value of f(0), f(1) and \(f\left(\left(\frac{1}{2}\right)^{\frac{1}{20}}\right)\) i.e., the largest value of {0, 0, –\(\frac{1}{4}\)}
Hence, the absolute maximum of f is 0 and the points of absolute maximum are 0 and 1. Further the absolute minimum is the least of 0, 0, -latex]\frac{1}{4}[/latex].
Hence the absolute minimum is -latex]\frac{1}{4}[/latex] and the point of absolute minimum is x = \(\left(\frac{1}{2}\right)^{\frac{1}{20}}\)