Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(c) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(c)
I.
Question 1.
Form the polynomial equation whose roots are
(i) 2 + 3i, 2 – 3i, 1 + i, 1 – i
Solution:
The required equation is [x – (2 + 3i)] [x – (2 – 3i)] [x – (1 + i)][x – (1 – i)] = 0
⇒ [(x – 2) – 3i)] [(x – 2) + 3i] [(x – 1) – i] [(x – 1) + i] = 0
⇒ [(x – 2)2 – 9i2] [(x – 1)2 – i2] = 0
⇒ (x2 – 4x + 4 + 9) (x2 – 2x + 1 + 1) = 0
⇒ (x2 – 4x + 13) (x2 – 2x + 2) = 0
⇒ x4 – 4x3 + 13x2 – 2x3 + 8x2 – 26x + 2x2 – 8x + 26 = 0
⇒ x4 – 6x3 + 23x2 – 34x + 26 = 0
(ii) 3, 2, 1 + i, 1 – i
Solution:
Required equation is (x – 3) (x – 2) [x – (1 + i)] [ x – (1 – i)] = 0
⇒ (x2 – 5x + 6) [(x – 1) – i] [(x – 1) + i] = 0
⇒ (x2 – 5x + 6) [(x – 1)2 – i2] = 0
⇒ (x2 – 5x + 6) (x2 – 2x + 1 + 1) = 0
⇒ (x2 – 5x + 6) (x2 – 2x + 2) = 0
⇒ x4 – 5x3 + 6x2 – 2x3 + 10x2 – 12x + 2x2 – 10x + 12 = 0
⇒ x4 – 7x3 + 18x2 – 22x + 12 = 0
(iii) 1 + i, 1 – i, -1 + i, -1 – i
Solution:
Required equation is [x – (1 + i)] [x – (1 – i)] [x – (-1 + i)] [x – (-1 – i)] = 0
⇒ [(x – 1) – i][(x – i) + i] [(x + 1) – i] [(x + 1) + i] = 0
⇒ [(x – 1)2 – i2] [(x + 1)2 – i2] = 0
⇒ (x2 – 2x + 1 + 1) (x2 + 2x + 1 + 1) = 0
⇒ (x2 – 2x + 2) (x2 + 2x + 2) = 0
⇒ x4 – 2x3 + 2x2 + 2x3 – 4x2 + 4x + 2x2 – 4x + 4 = 0
⇒ x4 + 4 = 0
(iv) 1 + i, 1 – i, 1 + i, 1 – i
Solution:
Required equation is [x – (1 + i)] [x – (1 – i)] [x – (1 + i)] [x – (1 – i)] = 0
⇒ [(x – 1) – i]2 [(x – 1) + i]2 = 0
⇒ [(x – 1)2 – i2] = 0
⇒ (x2 – 2x + 1 + 1)2 = 0
⇒ x4 + 4x2 + 4 – 4x3 + 4x2 – 8x = 0
⇒ x4 – 4x3 + 8x2 – 8x + 4 = 0
![]()
Question 2.
Form the polynomial equation with rational coefficients whose roots are
(i) 4√3, 5 + 2i
Solution:
For the polynomial equation with rational coeffs. the roots are conjugate surds and conjugate complex numbers.
4√3, 5 + 2i
Let α = 4√3 then β = -4√3, and γ = 5 + 2i then δ = 5 – 2i
α, β, γ, δ are the roots
α + β = 0, αβ = -48
γ + δ = 10, γδ = 25 + 4 = 29
The required equation is [x2 – (α + β)x + αβ] [x2 – (γ + δ)x + γδ] = 0
⇒ (x2 – 48) (x2 – 10x + 29) = 0
⇒ x4 – 10x3 + 29x2 – 48x2 + 480x – 1932 = 0
⇒ x4 – 10x3 – 19x2 + 480x – 1932 = 0
(ii) 1 + 5i, 5 – i
Solution:
For the polynomial equation with rational coeffs. the roots are conjugate surds and conjugate complex numbers.
Let α = 1 + 5i then β = 1 – 5i,
and γ = 5 + i then δ = 5 – i
α + β = 2, αβ = 26
γ + δ = 10, γδ = 26
The required equation is [x2 – (α + β)x + αβ] [x2 – (γ + δ)x + γδ] = 0
⇒ (x2 – 2x + 26) (x2 – 10x + 26) = 0
⇒ x4 – 12x3 + 72x2 – 312x + 676 = 0
(iii) i – √5
Solution:
For the polynomial equation with rational coeffs. the roots are conjugate surds and conjugate complex numbers.
Let α = i – √5, β = i + √5, γ = -i – √5, δ = -i + √5 are the roots
α + β = 2i, αβ = -6
γ + δ = -2i, γδ = -6
The required equation is [x2 – (α + β)x + αβ][x2 – (γ + δ)x + γδ] = 0
⇒ (x2 – 2ix – 6) (x2 + 2ix – 6) = 0
⇒ [(x2 – 6) – 2ix] [(x2 – 6) + 2ix] = 0
⇒ (x2 – 6)2 + 4x2 = 0
⇒ x4 + 36 – 12x2 + 4x2 = 0
⇒ x4 – 8x2 + 36 = 0
(iv) -√3 + i√2
Solution:
Let α = -√3 + i√2, β = -√3 – i√2, γ = √3 – i√2, γ = √3 + i√2
α + β = -2√3
αβ = (-√3)2 – (i√2)2
= 3 – i2 (2)
= 5
γ + δ = 2√3
γδ = 5
The required equation is [(x2 – (α + β)x + αβ)] [(x2 – (γ + δ)x + γδ)] = 0
⇒ (x2 + 2√3x + 5) (x2 – 2√3x + 5) = 0
⇒ (x2 + 5)2 – (2√3x)2 = 0
⇒ x4 + 25 + 10x2 – 12x2 = 0
⇒ x4 – 2x2 + 25 = 0
![]()
II.
Question 1.
Solve the equation x4 + 2x3 – 5x2 + 6x + 2 = 0 given that 1 + i is one of its roots.
Solution:
Let 1 + i be one root ⇒ 1 – i be another root
The equation having roots 1 ± i is x2 – 2x + 2 = 0
∴ x2 – 2x + 2 is a factor of x4 + 2x3 – 5x2 + 6x + 2 = 0

∴ The roots of the given equation are 1 ± i, -2 + √3
Question 2.
Solve the equation 3x3 – 4x2 + x + 88 = 0 which has 2 – √-7 as a root.
Solution:
Let 2 – √-7 (i.e) 2 – √7i is one root
⇒ 2 + √7i is another root.
The equation having roots 2 ± √7i is x2 – 4x + 11 = 0
∴ x2 – 4x + 11 is a factor of the given equation.
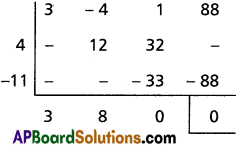
3x + 8 = 0
⇒ x = \(-\frac{8}{3}\)
∴ The roots of the given equation are 2 ± √7i, \(-\frac{8}{3}\)
![]()
Question 3.
Solve x4 – 4x2 + 8x + 35 = 0, given that 2 + i√3 is a root.
Solution:
Let 2 + i√3 be one root
⇒ 2 – i√3 is another root.
The equation having roots 2 ± i√3 is x2 – 4x + 7 = 0
∴ x2 – 4x + 7 is a factor of x4 – 4x2 + 8x + 35

∴ The roots of the given equation are 2 ± i√3, -2 ± i
Question 4.
Solve the equation x4 – 6x3 + 11x2 – 10x + 2 = 0, given that 2 + √3 is a root of the equation.
Solution:
2 + √3 is one root
⇒ 2 – √3 is another root.
The equation having the roots of 2 ± √3 is x2 – 4x + 1 = 0
∴ x2 – 4x + 1 is a factor of x4 – 6x3 + 11x2 – 10x + 2 = 0
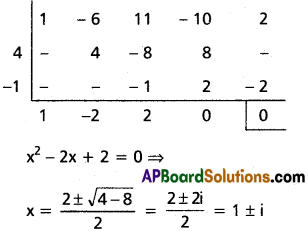
∴ The roots of the required equation are 2 ± √3, 1 ± i
Question 5.
Given that -2 + √-7 is a root of the equation x4 + 2x2 – 16x + 77 = 0, solve it completely.
Solution:
-2 – √-7 (i.e) -2 + i√7 is one root
⇒ -2 – i√7 is another root.
The equation having the roots of -2 ± i√7 is x2 + 4x + 11 = 0
∴ x2 + 4x + 11 is a factor of x4 + 2x2 – 16x + 77
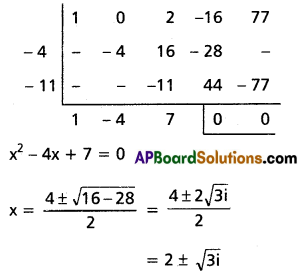
∴ The roots of the required equation are -2 ± i√7, 2 ± √3i
![]()
Question 6.
Solve the equations x4 + 2x3 – 16x2 – 22x + 7 = 0, given that 2 – √3 is a root of it.
Solution:
2 + √3 is a root ⇒ 2 – √3 is also a root.
The equation having roots 2 ± √3 is
x2 – (2 + √3 + 2 – √3)x + (2 + √3) (2 – √3) = 0
⇒ x2 – 4x + 1 = 0
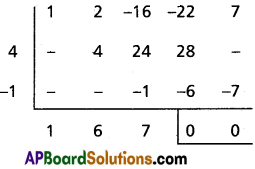
x2 + 6x + 7 = 0
⇒ x = \(\frac{-6 \pm \sqrt{36-28}}{2}\)
⇒ x = -3 ± √2
∴ Roots are 2 ± √3, -3 ± √2
Question 7.
Solve the equation 3x5 – 4x4 – 42x3 + 56x2 + 27x – 36 = 0 given that √2 + √5 is one of its roots.
Solution:
√2 + √5 is a root
⇒ -√2 – √5, -√2 + √5, -√2 – √5 are also roots.
The equation haying roots √2 + √5 is
x2 – (√2 + √5 + √2 – √5) + (√2 + √5) (√2 – √5) = 0
⇒ x2 – 2√2x – 3 = 0
The equation having roots -√2 ± √5 is
x2 – (-√2 + √5 – √2 – √5) + (√2 + √5)(-√2 – √5) = 0
⇒ x2 + 2√x – 3 = 0
The equation having roots ±√2 ± √5 is (x2 + 2√2x – 3) (x2 – 2√2x – 3) = 0
⇒ (x2 – 3)2 – (2√2x)2 = 0
⇒ x4 – 6x2 + 9 – 8x2 = 0
⇒ x4 – 14x2 + 9 = 0
∴ 3x5 – 4x4 – 42x3 + 56x2 + 27x – 36 = 0
⇒ 3x(x4 – 14x2 + 9) – 4(x4 – 14x2 + 9) = 0
⇒ (x4 – 14x2 + 9) (3x – 4) = 0
⇒ x = ±√2 ± √5 or 4/3
∴ The roots are ±√2 ± √5, 4/3
![]()
Question 8.
Solve the equation x4 – 9x3 + 27x2 – 29x + 6 = 0, given that one root of it is 2 – √3.
Solution:
2 – √3 is one root ⇒ 2 + √3 is another root.
The equation having the roots of 2 ± √3 is x2 – 4x + 1 = 0
∴ x2 – 4x + 1 is a factor of the given equation.
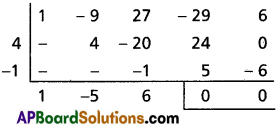
x2 – 5x + 6 = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, 3
∴ The roots of the required equations are 2 ± √3, 2, 3
Question 9.
Show that the equation \(\frac{a^{2}}{x-a^{\prime}}+\frac{b^{2}}{x-b^{\prime}}+\frac{c^{2}}{x-c^{\prime}}+\ldots+\frac{k^{2}}{x-k^{\prime}}\)= x – m Where a, b, c ….k, m, a’, b’, c’…. k’ are all real numbers, cannot have a non-real root.
Solution:
Let α + iβ be the root of the given equation.
Suppose if β ≠ 0, then α – iβ is also a root of the given equation.
Substitute α + iβ in the given equation, and we get

\(\left[\frac{a^{2}}{\left(\alpha-a^{\prime}\right)^{2}+\beta^{2}}+\frac{b^{2}}{\left(\alpha-b^{\prime}\right)^{2}+\beta^{2}}+\ldots \frac{k^{2}}{\left(\alpha-k^{\prime}\right)^{2}+\beta^{2}}+1\right]\)
= 0
⇒ β = 0
This is a contradiction.
∴ The given equation cannot have non-real roots.