Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(b)
I.
Question 1.
Solve x3 – 3x2 – 16x + 48 = 0, given that the sum of two roots is zero.
Solution:
Let α, β, γ are the roots of x3 – 3x2 – 16x + 48 = 0
α + β + γ = 3
Given α + β = 0 (∵ Sum of two roots is zero)
∴ γ = 3
i.e. x – 3 is a factor of x3 – 3x2 – 16x + 48 = 0

x2 – 16 = 0
⇒ x2 = 16
⇒ x = ±4
∴ The roots are -4, 4, 3
![]()
Question 2.
Find the condition that x3 – px2 + qx – r = 0 may have the sum of its roots zero.
Solution:
Let α, β, γ be the roots of x3 – px2 + qx – r = 0
α + β + γ = p ………(1)
αβ + βγ + γα = q ………..(2)
αβγ = r ………..(3)
Given α + β = 0 (∵ Sum of two roots is zero)
From (1), γ = p
∴ γ is a root of x3 – px2 + qx – r = 0
γ3 – pγ2 + qγ – r = 0
But γ = p
p3 – p(p2) + q(p) – r = 0
p3 – p2 + qp – r = 0
∴ qp = r is the required condition.
Question 3.
Given that the roots of x3 + 3px2 + 3qx + r = 0 are in
(i) A.P., show that 2p3 – 3qp + r = 0
(ii) G.P., show that p3r = q3
(iii) H.P., show that 2q3 = r(3pq – r)
Solution:
Given equation is x3 + 3px2 + 3qx + r = 0
(i) The roots are in A.P.
Suppose a – d, a, a + d are the roots
Sum = a – d + a + a + d = -3p
⇒ 3a = -3p
⇒ a = -p ……….(1)
∵ ‘a’ is a root of x3 + 3px2 + 3qx + r = 0
⇒ a3 + 3pa2 + 3qa + r = 0
But a = -p
⇒ p3 + 3p(-p)2 + 3q(-p) + r = 0
⇒ 2p3 – 3pq + r = 0 is the required condition
(ii) The roots are in G.P.
Suppose the roots be \(\frac{a}{R}\), a, aR
Given (\(\frac{a}{R}\)) (a) (aR) = -r
⇒ a = -r
⇒ a = (-r)1/3
∵ ‘a’ is a root of x3 + 3px2 + 3qx + r = 0
⇒ (-r1/3)3 + 3p(-r1/3)2 + 3q(-r1/3) + r = 0
⇒ -r + 3pr2/3 – 3qr1/3 + r = 0
pr2/3 = qr1/3
⇒ pr1/3 = q
⇒ p1/3r = q is the required condition
(iii) The roots of x3 + 3px2 + 3qx + r = 0 are in H.P.
x3 + 3px2 + 3qx + r = 0 ……..(1)
Let y = \(\frac{1}{x}\) so that \(\frac{1}{y^{3}}+\frac{3 p}{y^{2}}+\frac{3 q}{y}+r\) = 0
Roots of ry3 + 3qy2 + 3py + 1 = 0 are in A.P.
ry3 + 3qy2 + 3py + 1 = 0 ……..(2)
Suppose a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = \(-\frac{3 q}{r}\)
3a = \(-\frac{3 q}{r}\)
a = \(-\frac{q}{r}\) ………(1)
∵ ‘a’ is a root of ry3 + 3qy2 + 3py + 1 = 0
⇒ ra3 + 3qa2 + 3pa + 1 = 0
But a = \(-\frac{q}{r}\)
⇒ \(r\left(-\frac{q}{r}\right)^{3}+3 q\left(-\frac{q}{r}\right)^{2}+3 p\left(-\frac{q}{r}\right)+1=0\)
⇒ \(\frac{-q^{3}}{r^{2}}+\frac{3 q^{3}}{r^{2}}-\frac{3 p q}{r}+1=0\)
⇒ -q3 + 3q3 – 3pqr + r2 = 0
⇒ 2q3 = r(3pq – r) is the required condition.
![]()
Question 4.
Find the condition that x3 – px2 + qx – r = 0 may have the roots in G.P.
Solution:
Let \(\frac{a}{R}\), a, aR be the roots of x3 – px2 + qx – r = 0
The product of the roots = \(\frac{a}{R}\) . a . aR = a3
product of the roots = r
⇒ a = r1/3
∵ a is a root of x3 – px2 + qx – r = 0
⇒ a3 – pa2 + qa – r = 0
But a = r1/3
⇒ (r1/3)3 – p(r1/3)2 + q(r1/3) – r = 0
⇒ r – p . r2/3 + q . r1/3 – r = 0
⇒ p . r2/3 = qr1/3
By cubing on both sides
⇒ p3r2 = q3r
⇒ p3r = q3 is the required condition
II.
Question 1.
Solve 9x3 – 15x2 + 7x – 1 = 0, given that two of its roots are equal.
Solution:
Suppose α, β, γ are the roots of 9x3 – 15x3 + 7x – 1 = 0
α + β + γ = \(\frac{15}{9}=\frac{5}{3}\)
αβ + βγ + γα = \(\frac{7}{9}\)
αβγ = \(\frac{1}{9}\)
Given α = β (∵ two of its roots are equal)
2α + γ = \(\frac{5}{3}\)
⇒ γ = \(\frac{5}{3}\) – 2α
α2 + 2αγ = \(\frac{7}{9}\)
⇒ α2 + 2α (\(\frac{5}{3}\) – 2α) = \(\frac{7}{9}\)
⇒ α2 + \(\frac{2 \alpha(5-6 \alpha)}{3}=\frac{7}{9}\)
⇒ 9α2 + 6α(5 – 6α) = 7
⇒ 9α2 + 30α – 36α2 = 7
⇒ 27α2 – 30α + 7 = 0
⇒ (3α – 1)(9α – 7) = 0
⇒ α = \(\frac{1}{3}\) or \(\frac{7}{9}\)

The roots are \(\frac{1}{3}\), \(\frac{1}{3}\), 1
![]()
Question 2.
Given that one root of 2x3 + 3x2 – 8x + 3 = 0 is double of another root, find the roots of the equation.
Solution:
Suppose α, β, γ are the roots of 2x3 + 3x2 – 8x + 3 = 0
α + β + γ = \(-\frac{3}{2}\) ……..(1)
αβ + βγ + γα = -4 ……..(2)
αβγ = \(-\frac{3}{2}\)
Given α = 2β (∵ one root is double the other)
Substituting in (1)
3β + γ = \(-\frac{3}{2}\)
⇒ γ = \(-\frac{3}{2}\) – 3β …….(4)
Substituting in (2)
αβ + γ(α + β) = -4
⇒ 2β2 + 3βγ = -4
⇒ 2β2 + 3β(\(-\frac{3}{2}\) – 3β) = -4
⇒ 2β2 – \(\frac{3 \beta(3+6 \beta)}{2}\) = -4
⇒ 4β2 – 9β – 18β2 = -8
⇒ 14β2 + 9β – 8 = 0
⇒ (2β – 1)(7β + 8) = 0
⇒ 2β – 1 = 0 or 7β + 8 = 0
⇒ β = \(\frac{1}{2}\) or β = \(-\frac{8}{7}\)

∴ The roots are \(\frac{1}{2}\), 1 and -3
Question 3.
Solve x3 – 9x2 + 14x + 24 = 0, given that two of the roots are in the ratio 3 : 2.
Solution:
Suppose α, β, γ are the roots of x3 – 9x2 + 14x + 24 = 0
α + β + γ = 9 ………(1)
αβ + βγ + γα = 14 ……….(2)
αβγ = -24 ……….(3)
∵ two roots are in the ratio 3 : 2
Let α : β = 3 : 2
⇒ β = \(\frac{2 \alpha}{3}\)
Substituting in (1)
\(\frac{5 \alpha}{3}\) + γ = 9
⇒ γ = 9 – \(\frac{5 \alpha}{3}\) ………(4)
Substituting in (2)
⇒ \(\frac{2}{3}\) α2 + γ(α + β) = 14
⇒ \(\frac{2}{3} \alpha^{2}+\left(9-\frac{5 \alpha}{3}\right) \cdot \frac{5 \alpha}{3}\) = 14
⇒ 2α2 + 5α(9 – \(\frac{5 \alpha}{3}\)) = 42
⇒ 2α2 + 5α \(\frac{(27-5 \alpha)}{3}\) = 42
⇒ 6α2 + 135α – 25α2 = 126
⇒ 19α2 – 135α + 126 = 0
⇒ 19α2 – 114α – 21α + 126 = 0
⇒ 19α(α – 6) – 21(α – 6) = 0
⇒ (19α – 21)(α – 6) = 0
⇒ 19α – 21 = 0 or α – 6 = 0
⇒ α = \(\frac{21}{19}\) or α = 6
Case (i): α = 6
β = \(\frac{2 \alpha}{3}\)
= \(\frac{2}{3}\) × 6
= 4
γ = 9 – \(\frac{5 \alpha}{3}\)
= 9 – \(\frac{5}{3}\) × 6
= 9 – 10
= -1
α = 6, β = 4, γ = -1 satisfy αβγ = -24
∴ The roots are 6, 4, -1
Case (ii): α = \(\frac{21}{19}\)
β = \(\frac{2}{3} \times \frac{21}{19}=\frac{14}{19}\)
γ = 9 – \(\frac{5 \alpha}{3}\)
= 9 – \(\frac{5}{3} \cdot \frac{21}{19}\)
= \(\frac{136}{19}\)
These values do not satisfy αβγ= -24
∴ The roots are 6, 4, -1.
![]()
Question 4.
Solve the following equations, given that the roots of each are in A.P.
(i) 8x3 – 36x2 – 18x + 81 = 0
Solution:
Given the roots of 8x3 – 36x2 – 18x + 81 = 0 are in A.P.
Let the roots be a – d, a, a + d
Sum of the roots = \(\frac{36}{8}\)
⇒ a – d + a + a + d = \(\frac{9}{2}\)
⇒ 3a = \(\frac{9}{2}\)
⇒ a = \(\frac{3}{2}\)
∴ (x – \(\frac{3}{2}\)) is a factor of 8x3 – 36x2 – 18x + 81 = 0

⇒ 8x2 – 24x – 54 = 0
⇒ 4x2 – 12x – 27 = 0
⇒ 4x2 – 18x + 6x – 27 = 0
⇒ 2x(2x – 9) + 3(2x – 9) = 0
⇒ (2x + 3) (2x – 9) = 0
⇒ x = \(-\frac{3}{2}, \frac{9}{2}\)
∴ The roots are \(-\frac{3}{2}, \frac{3}{2}, \frac{9}{2}\)
(ii) x3 – 3x2 – 6x + 8 = 0
Solution:
The roots of x3 – 3x2 – 6x + 8 = 0 are in A.P
Suppose a – d, a, a + d be the roots
Sum = a – d + a + a + d = 3
⇒ 3a = 3
⇒ a = 1
∴ (x – 1) is a factor of x3 – 3x2 – 6x + 8 = 0

⇒ x2 – 2x – 8 = 0
⇒ x2 – 4x + 2x – 8 = 0
⇒ x(x – 4)+ 2(x – 4) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x = 4, -2
∴ The roots are -2, 1, 4
Question 5.
Solve the following equations, given that the roots of each are in G.P.
(i) 3x3 – 26x2 + 52x – 24 = 0
Solution:
Given equation is 3x3 – 26x2 + 52x – 24 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar are the roots.
Product = \(\frac{a}{r}\) . a . ar = \(-\left(-\frac{24}{3}\right)\)
⇒ a3 = 8
⇒ a = 2
∴ (x – 2) is a factor of 3x3 – 26x2 + 52x – 24
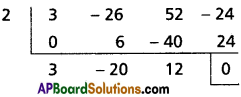
Hint: 3 × 12 = 3 ×6 × 2 = (-18)(-2)
⇒ 3x2 – 20x + 12 = 0
⇒ 3x2 – 18x – 2x + 12 = 0
⇒ 3x(x – 6) – 2(x – 6) = 0
⇒ (3x – 2) (x – 6) = 0
⇒ x = \(\frac{2}{3}\), 6
∴ The roots are \(\frac{2}{3}\), 2, 6.
(ii) 54x3 – 39x2 – 26x + 16 = 0
Solution:
Given equation is 54x3 – 39x2 – 26x + 16 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar be the roots.
Product = \(\frac{a}{r}\) . a . ar = \(-\frac{16}{54}\)

Hint: 18 × 8 = 9 × 2 × 8 = (-9) (-16)
⇒ 54x2 – 75x + 24 = 0
⇒ 18x2 – 25x + 8 = 0
⇒ 18x2 – 9x – 16x + 8 = 0
⇒ 9x(2x – 1) – 8(2x- 1) = 0
⇒ (9x – 8) (2x – 1) = 0
⇒ x = \(\frac{8}{9}, \frac{1}{2}\)
∴ The roots are \(\frac{8}{9},-\frac{2}{3}, \frac{1}{2}\)
![]()
Question 6.
Solve the following equations, given that the roots of each are in H.P.
(i) 6x3 – 11x2 + 6x – 1 = 0
Solution:
Given equation is 6x3 – 11x2 + 6x – 1 = 0 …….(1)
Put y = \(\frac{1}{x}\) so that \(\frac{6}{\mathrm{y}^{3}}-\frac{11}{\mathrm{y}^{2}}+\frac{6}{\mathrm{y}}-1\) = 0
⇒ 6 – 11y + 6y2 – y3 = 0
⇒ y3 – 6y2 + 11y – 6 = 0 ………(2)
Roots of (1) are in H.P.
⇒ Roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = 6
⇒ 3a = 6
⇒ a = 2
Product = a(a2 – d2) = 6
⇒ 2(4 – d2) = 6
⇒ 4 – d2 = 3
⇒ d2 = 1
⇒ d = 1
a – d = 2 – 1 = 1,
a = 2
a + d = 2 + 1 = 3
The roots of (2) are 1, 2, 3
The roots of (1) are 1, \(\frac{1}{2}\), \(\frac{1}{3}\)
(ii) 15x3 – 23x2 + 9x – 1 = 0
Solution:
Given equation is 15x3 – 23x2 + 9x – 1 = 0 …….(1)
Put y = \(\frac{1}{x}\) so that \(\frac{15}{y^{3}}-\frac{23}{y^{2}}+\frac{9}{y}-1\) = 0
⇒ 15 – 23y + 9y2 – y3 = 0
⇒ y3 – 9y2 + 23y – 15 = 0 ………(2)
Roots of (1) are in H.P. So that roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = 9
⇒ 3a = 9
⇒ a = 3
Product = a(a2 – d2) = 15
⇒ 3(9 – d2) = 15
⇒ 9 – d2 = 5
⇒ d2 = 4
⇒ d = 2
a – d = 3 – 2 = 1
a = 3
a + d = 3 + 2 = 5
Roots of (2) are 1, 3, 5
Hence roots of (1) are 1, \(\frac{1}{3}\), \(\frac{1}{5}\)
![]()
Question 7.
Solve the following equations, given that they have multiple roots.
(i) x4 – 6x3 + 13x2 – 24x + 36 = 0
Solution:
(i) Let f(x) = x4 – 6x3 + 13x2 – 24x + 36
⇒ f'(x) = 4x3 – 18x2 + 26x – 24
⇒ f'(3) = 4(27) – 18(9) + 26(3) – 24
⇒ f'(3) = 108 – 162 + 78 – 24
⇒ f'(3) = 0
f(3) = 81 – 162 + 117 – 72 + 36 = 0
Hint: Choose the value of x from the factors of the G.C.D of constant terms in f(x) and f'(x).
∴ x – 3 is a factor of f'(x) and f(x)
∴ 3 is the repeated foot of f(x)
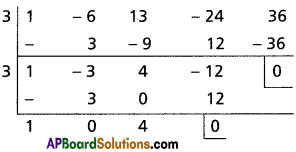
x2 + 4 = 0
⇒ x = ±2i
∴ The roots of the given equation are 3, 3, ±2i
(ii) 3x4 + 16x3 + 24x2 – 16 = 0
Solution:
Let f(x) = 3x4 + 16x3 + 24x2 – 16
f(x) = 12x3 + 48x2 + 48x
= 12x(x2 + 4x + 4)
= 12x (x + 2)2
f'(-2) = 0
f(-2) = 3(16) + 16(-8) + 24(4) – 16 = 0
∴ x + 2 is a factor of f'(x) and f(x)
∴ -2 is a multiple root of f(x) = 0
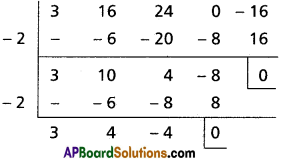
3x2 + 4x – 4 = 0
⇒ 3x2 + 6x – 2x – 4 = 0
⇒ 3x(x + 2) – 2(x + 2) = 0
⇒ (x + 2) (3x – 2) = 0
⇒ x = -2, \(\frac{2}{3}\)
∴ The roots of the given equation are -2, -2, -2, \(\frac{2}{3}\)
III.
Question 1.
Solve x4 + x3 – 16x2 – 4x + 48 = 0, given that the product of two of the roots is 6.
Solution:
Suppose α, β, γ, δ are the roots of
x4 + x3 – 16x2 – 4x + 48 = 0 ………..(1)
Sum of the roots = -1
⇒ α + β + γ + δ = -1
and Product of the roots = αβγδ = 48
∵ Product of two roots is 6
Let αβ = 6
From (1), γδ = \(\frac{48}{\alpha \beta}=\frac{48}{6}\) = 8
Let α + β = p and γ + δ = q
The equation having roots α, β is x2 – (α + β) x + αβ = 0
⇒ x2 – px + 6 = 0 ………..(2)
The equation having the roots γ, δ is x2 – (γ + δ) x + γδ = 0
⇒ x2 – qx + 8 = 0 ……….(3)
∴ From (1), (2) and (3)
x4 + x3 – 16x2 – 4x + 48 = (x2 – px + 6) (x2 – qx + 8)
= x4 – (p + q) x3 + (pq + 14) x2 – (8p + 86q) x + 48
Comparing the like terms,
p + q = -1
8p + 6q = 4 ⇒ 4p + 3q = 2
Solving, q = -6
∴ p = -1 + 6 = 5
Substitute the value of p in eq. (2),
x2 – 5x + 6 = 0 ⇒ x = 2, 3
Substitute/the value of q in eq. (3),
x2 + 6x + 8 = 0 ⇒ x = -2, – 4
∴ The roots of the given equation are -4, -2, 2, 3
![]()
Question 2.
Solve 8x4 – 2x3 – 27x2 + 6x + 9 = 0 given that two roots have the same absolute value, but are opposite in signs.
Solution:
Suppose α, β, γ, δ are the roots of the equation
8x4 – 2x3 – 27x2 + 6x + 9 = 0
⇒ \(x^{4}-\frac{1}{4} x^{3}-\frac{27}{8} x^{2}+\frac{3}{4} x+\frac{9}{8}=0\) …………(1)
Sum of the roots = α + β + γ + δ = \(\frac{1}{4}\) and
Product of the roots = αβγδ = \(\frac{9}{8}\)
Given β = -α
⇒ α + β = 0
∴ 0 + γ + δ = \(\frac{1}{4}\)
⇒ γ + δ = \(\frac{1}{4}\)
Let αβ = p, γδ = q, so that pq = \(\frac{9}{8}\)
The equation having the roots α, β is x2 – (α + β)x + αβ = 0
⇒ x2 + p = 0 ……….(2)
The equation having the roots γ, δ is x2 – (γ + δ)x + γδ = 0
⇒ x2 – \(\frac{1}{4}\) x + q = 0 ……..(3)
From (1), (2) and (3)
\(x^{4}-\frac{1}{4} x^{3}-\frac{27}{8} x^{2}+\frac{3}{4} x+\frac{9}{8}\) = (x2 + p) \(\left(x^{2}-\frac{1}{4} x+q\right)\)
= \(x^{4}-\frac{1}{4} x^{3}+(p+q) x^{2}-\frac{p}{4} x+p q\)
Comparing the coefficients of x and constants
\(\frac{-p}{4}=\frac{3}{4}\) ⇒ p = -3
pq = \(\frac{9}{8}\)
⇒ q = \(\frac{9}{8} \times \frac{-1}{3}=\frac{-3}{8}\)
Substitute the value of p in eq. (2),
x2 – 3 = 0 ⇒ x = ±√3
Substitute the value of q in eq. (3),
\(x^{2}-\frac{1}{4} x-\frac{3}{8}=0\)
⇒ 8x2 – 2x – 3 = 0
⇒ (2x + 1) (4x – 3) = 6
⇒ x = \(-\frac{1}{2}, \frac{3}{4}\)
∴ The roots of the given equation are -√3, \(-\frac{1}{2}, \frac{3}{4}\), √3
Question 3.
Solve 18x3 + 81x2 + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots.
Solution:
Suppose α, β, γ are the roots of 18x3 + 81x2 + 121x + 60 = 0
sum = α + β + γ = \(\frac{-81}{18}=\frac{-9}{2}\) ……….(1)
αβ + βγ + γα = \(\frac{121}{18}\) …………(2)
αβγ = \(\frac{-60}{18}=\frac{-10}{3}\) ………(3)
∵ One root is equal to half of the sum of the remaining two,
Let α = \(\frac{1}{2}\) (β + γ)
Substitute in (1)

Question 4.
Find the condition in order that the equation ax4 + 4bx3 + 6cx2 + 4dx + e = 0 may have a pair of equal roots.
Solution:
Let α, α, β, β are the roots of the equation.
ax4 + 4bx3 + 6cx2 + 4dx + e = 0
⇒ \(x^{4}+\frac{4 b}{a} x^{2}+\frac{6 c}{a} x^{2}+\frac{4 d}{a} x+\frac{e}{a}=0\)
Sum of the roots, 2(α + β) = \(-\frac{4 b}{a}\)
⇒ α + β = \(-\frac{2 b}{a}\)
⇒ αβ = k (say)
Equation having roots α, β is x2 – (α + β) x + αβ = 0

Question 5.
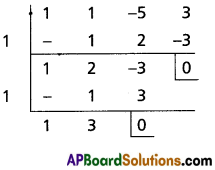
(i) Show that x5 – 5x3 + 5x2 – 1 = 0 has three equal roots and find this root.
Solution:
Let f(x) = x5 – 5x3 + 5x2 – 1
f'(x) = 5x4 – 15x2 + 10x = 5x(x3 – 3x + 2)
f'(1) = 5(1) (1 – 3 + 2) = 0
f(1) = 1 – 5 + 5 – 1 = 0
x – 1 is a factor of f'(x) and f(x)
∴ 1 is a repeated root of f(x).
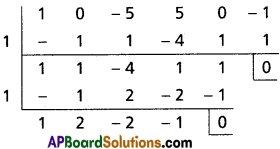
x3 + 2x2 – 2x – 1 = 0
⇒ 1 is a root of the above equation (∵ sum of the coefficients is zero)
∴ 1 is the required root.
(ii) Find the repeated roots of x5 – 3x4 – 5x3 + 27x2 – 32x + 12 = 0
Solution:
Let f(x) = x5 – 3x4 – 5x3 + 27x2 – 32x + 12
f'(x) = 5x4 – 12x3 – 15x2 + 54x – 32
f'(2) = 5(2)4 – 12(2)3 – 15(2)2 + 54(2) – 32
= 80 – 96 – 60 + 108 – 32
= 0
f(2) = (2)5 – 3(2)4 – 5(2)3 + 27(2)2 – 32(2) + 12
= 32 – 48 – 40 + 108 – 64 + 12
= 152 – 152
= 0
∴ x – 2 is a common factor of f'(x) and f(x)
2 is a multiple root of f(x) = 0
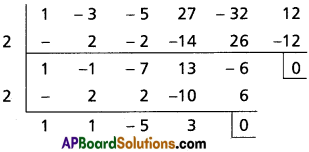
Let g(x) = x3 + x2 – 5x + 3
g'(x) = 3x2 + 2x – 5 = (3x + 5) (x – 1)
g(1) = 1 + 1 – 5 + 3 = 0
∴ x – 1 is a common factor of g'(x) and g(x)
∴ 1 is a multiple root of g(x) = 0
x + 3 = 0 ⇒ x = -3
∴ The roots are 2, 2, 1, 1, -3
![]()
Question 6.
Solve the equation 8x3 – 20x2 + 6x + 9 = 0 given that the equation has multiple roots.
Solution:
Let f(x) = 8x3 – 20x2 + 6x + 9
f'(x) = 24x2 – 40x + 6
= 2 (12x2 – 20x + 3)
= 2[12x2 – 18x – 2x + 3]
= 2[6x(2x – 3) – 1(2x – 3)]
= 2(2x – 3) (6x – 1)
f'(x) = 0
⇒ x = \(\frac{3}{2}\), x = \(\frac{1}{6}\)
\(f\left(\frac{3}{2}\right)=8\left(\frac{3}{2}\right)^{3}-20\left(\frac{3}{2}\right)^{2}+6\left(\frac{3}{2}\right)+9\)
= 27 – 45 + 9 + 9
= 0
Hence x – \(\frac{3}{2}\) is a factor of f(x) and f'(x)
∴ \(\frac{3}{2}\) is a multiple root of f(x) = 0
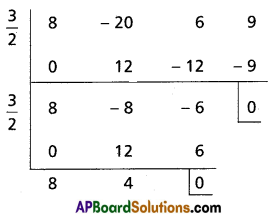
8x – 4 = 0
⇒ x = \(\frac{4}{8}=\frac{1}{2}\)
∴ The roots of the equation f(x) = 0 are \(\frac{3}{2}, \frac{3}{2}, \frac{1}{2}\)