Inter 2nd Year Maths 2B Parabola Important Questions

Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Parabola Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2B Parabola Important Questions

Question 1.
Find the equation of the parabola whose focus is S (1, -7) and vertex is A(1, -2). [T.S. Mar. 15]
Solution:
Let S = (1, -7), A(1, -2)
h = 1, k = -2, a = -2 + 7 = 5
Axis of the parabola is parallel to y – axis
Equation of the parabola is
(x – h)² = – 4a (y – k)
(x – 1)² = – 20(y + 2)
x² – 2x + 1, = – 20y – 40
⇒ x² – 2x + 20y + 41 – 0.

Question 2.
If the normal at the point t₁ on the parabola y² =, 4ax meets it again at point t² then prove that t₁t₂ + t₁² + 2 = 0. [May 07]
Solution:
Equation of normal is
y – y₁ = \(\frac{-y_{1}}{2 a}\) (x – x₁)
y – 2at₁ = \(\frac{-2 a t_{1}}{2 a}\) (x – at₁²) ……………… (i)
Equation of the line (i) again meets parabola at (at₂², 2at₁)
∴ 2at₂ – 2at₁ = t₁ (at₂² – at₁²)
\(-\frac{2}{t_{1}}\) = t₁ + t₂ ⇒ -2 = t₁² + t₁t₂
⇒ t₁² + t₁t₂ + 2 = 0

Question 3.
Find the coordinates of the vertex and focus, and the equations of the directrix and axes of the y – x + 4y + 5 = 0. [Mar 05]
Solution:
y² – x + 4y + 5 = 0 ⇒ (y – (-2))² = (x – 1), comparing with (y – k)² = 4a(x – h),we get (h, k) = (1, -2) and a = \(\frac{1}{4}\), coordinates of the vertex (h, k) = (1 ,-2)
coordinates of the focus (h + a, k) = (\(\frac{5}{4}\), -2)
Equation of the directrix x – h + a = 0
i.e., 4x – 3 = 0
Equation of the axis y – k = 0.
i.e., y + 2 = 0

Question 4.
Find the coordinates of the points on the parabola y² = 2x whose focal distance is \(\frac{5}{2}\). [A.P. Mar. 15, Mar. 13]
Solution:
Let P(x₁, y₁) be a point on the parabola
y² = 2x whose focal distance is \(\frac{5}{2}\) then
y₁² = 2x₁ and x₁ + a = \(\frac{5}{2}\)
⇒ x₁ + \(\frac{1}{2}\) = \(\frac{5}{2}\) ⇒ x₁ = 2
∴ y₁² = 2(2) = 4 ⇒ y₁ = ±2
∴ The required points are (2, 2) and (2, -2)

Question 5.
Find the value of k if the line 2y = 5x + k is a tangent to the parabola y² = 6x. [T.S. Mar. 16]
Solution:
Given line is 2y = 5x + k
⇒ y = (\(\frac{5}{2}\))x + (\(\frac{k}{2}\))
Comparing y = (\(\frac{5}{2}\))x + (\(\frac{k}{2}\)) with y = mx + c
We get m = \(\frac{5}{2}\), c = \(\frac{k}{2}\)
y = (\(\frac{5}{2}\))x + \(\frac{k}{2}\) is a tangent to y² = 6x
c = \(\frac{a}{m}\)
⇒ \(\frac{k}{2}=\frac{\left(\frac{3}{2}\right)}{\left(\frac{5}{2}\right)}\) ⇒ k = \(\frac{6}{5}\)

Question 6.
Show that the equations of common tangents to the circle x² + y² = 2a² and the parabola y² = 8ax are y = ± (x + 2a). [Mar. 06]
Solution:
The equation of tangent to parabola
y² = 8ax is y = mx + \(\frac{2a}{m}\)
m²x – my + 2a = 0 ……………….. (1)
If (i) touches circle x² + y² = 2a², then the length of perpendicular from its centre (0, 0) to (i) must be equal to the radius a\(\sqrt{2}\) of the circle.
\(\left|\frac{2 a}{\sqrt{m^{2}+m^{4}}}\right|=a \sqrt{2}\)
or 4 = 2 (m⁴ + m²)
m⁴ + m² – 2 = 0
(m² + 2) (m² – 1) = 0 or m = ±1
Required tangents are
y = (1) x + \(\frac{2 a}{(1)}\), y = (-1) x + \(\frac{2 a}{(-1)}\)
y = ± (x + 2a)

Question 7.
Find the co-ordinates of the point on the parabola y² = 8x whose focal distance is 10. [T.S. Mar. 17] [A.P. Mar. 16; Mar. 14, 11]
Solution:
Equation of the parabola is
y² = 8x
4a = 8 ⇒ a – 2

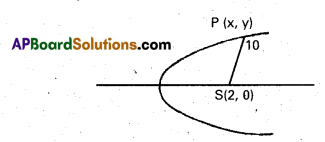
Co-ordinates of the focus S are (2, 0) Suppose P(x, y) is the point on the parabola.
Given SP = 10 ⇒ SP² = 100
(x – 2)² + y² = 100
But y² = 8x
⇒ (x – 2)² + 8x = 100
⇒ x² – 4x + 4 + 8x – 100 = 0
⇒ x² + 4x – 96 = 0 ⇒ (x + 12) (x – 8) = 0
x + 12 = 0 or x – 8 = 0
x = -12, or 8
Case (i) x = 8
y² = 8.x = 8.8 = 64
y = ±8
Co-ordinates of the required points are (8, 8) and (8, -8)
Case (ii) x = -12
y² = 8(-12) = -96 < 0
y is not real.

Question 8.
If (\(\frac{1}{2}\), 2) is one extermity of a focal chord of the parabola y² = 8x. Find the co-ordinates of the other extremity. [May 06]
Solution:
A = (\(\frac{1}{2}\), 2); S = (2, 0)
B = (x₁, y₁) ⇒ (\(\frac{y_{1}^{2}}{8}\), y₁)
ASB is a focal chord.
∴ Slopes of SA and BS are same.

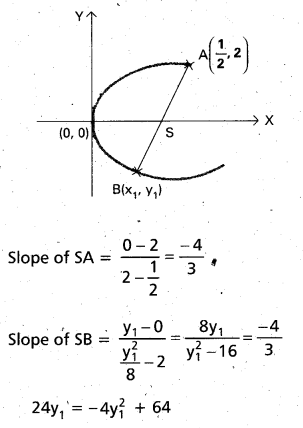
or 4y₁² + 24y₁ – 64 = 0
⇒ y₁² + 6y₁ – 16 = 0
⇒ (y₁ + 8) (y, – 2) = 0
y₁ = 2, 8
x₁ = \(\frac{1}{2}\), 8; So (8, -8) other extremity.

Question 9.
Show that the common tangent to the parabola y² = 4ax and x² = 4by is xa^1/3 + yb^1/3 + a^2/3b^2/3 = 0 [T.S. Mar. 17] [A.P. Mar. 16]
Solution:
The equations of the parabolas are
y² = 4ax ………………. (1)
and x² = 4by ……………… (2)
Equation of any tangent to (1) is of the form
y = mx + \(\frac{a}{m}\) …………….. (3)
If the line (3) is a tangent to (2) also, we must get only one point of intersection of (2) and (3).
Substituting the value of y from (3) in (2), we get x² = 4b (mx + \(\frac{a}{m}\)) is 3x² – 4bm²x – 4ab = 0 should have equal roots Therefore its discriminent must be zero. Hence
16b²m⁴ – 4m (-4ab) = 0
16b(bm⁴ + am) = 0
m(bm³ + a) = 0 But m ≠ 0
∴ m = – a^1/3/b^1/3 substituting in (3) the equation of the common tangent becomes
y = \(-\left(\frac{a}{b}\right)^{1 / 3} x+\frac{a}{\left(-\frac{a}{b}\right)^{1 / 3}}\) or
a^1/3x + b^1/3y + a^2/3b^2/3 = 0 .

Question 10.
Prove that the area of the triangle formed by the .tangents at (x₁, y₁), (x₂, y₂) and (x₃, y₃) to the parabola y² = 4ax (a > 0) is \(\frac{1}{16a}\)|(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units. [T.S. Mar. 15]
Solution:
Let D(x₁, y₁) = (at₁², 2at₁),
E(x₂, y₂) = (at₂², 2at₂),
and F(x₃, y₃) = (at₃², 2at₃), be three points on the parabola
y² = 4ax (a > 0).
The equation of the tangents at D, E and F are
t₁y = x + at₁² ……………… (1)
t₂y = x + at₂² ………………. (2)
t₃y = x.+ at₃² ………………. (3)
(1) – (2) ⇒ (t₁ – t₂) y = a(t₁ – t₂) (t₁ + t₂)
⇒ y = a(t₁ + t₂) substituting in (1)
we get x = at₁t₂.
∴ The point of intersection of the tangents at D and E is say P(at₁t₂, a(t₁ + t₂))
Similarly the points of intersection of tangent at E, F and at F, D are Q(at₂t₃, a(t₂ + t₃) and R(at₃t₁ a(t₃ + t₁)) respectively
Area of ∆PQR

\(\frac{1}{16a}\) |2a(t₁ – t₂) 2a(t₂ – t₃) 2a(t₃ – t₁)|
\(\frac{1}{16a}\)|(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units.

Question 11.
Prove that the two parabolas y² = 4ax and x² = 4by intersect (other than the origin) at an angle of Tan^-1 \(\left[\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\right]\) [Mar. 14]
Solution:
Without loss of generality we assume a > 0 and b > 0.
Let P(x, y) be the point of intersection of the parabolas other than the origin. Then
y⁴ = 16a²x²
= 16a²(4by)
= 64a²by
∴ y[y³ – 64a²b] = 0
=> y³ – 64a²b = 0
=> y = (64a²b)^1/3 [∵ y > 0]
= 4a^2/3b^1/3

Also from y² = 4ax, x = \(\frac{16 a^{4 / 3} b^{2 / 3}}{4 a}\)
= 4a^1/3b^2/3
∴ P = (4a^1/3b^2/3, 4a^2/3b^1/3)
Differentiating both sides of y² 4ax w.r.t ‘x’, we get
\(\frac{d y}{d x}=\frac{2 a}{y}\)
∴ \(\left[\frac{\mathrm{dy}}{\cdot \mathrm{dx}}\right]_{\mathrm{p}}=\frac{2 \mathrm{a}}{4 \mathrm{a}^{2 / 3} \mathrm{~b}^{1 / 3}}=\frac{1}{2}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{1 / 3}\)
If m₁ be the slope of the tangent at P to y² = 4ax, then
m₁ = \(\frac{1}{2}\left(\frac{a}{b}\right)^{1 / 3}\)
Similarly, we get m₂ = \(2\left(\frac{a}{b}\right)^{1 / 3}\) where m₂ is the slope of the tangent at P to x² = 4by.
If θ is the acute angle between the tangents to the curves at P, then
tan θ = \(\left|\frac{m_{2}-m_{1}}{1+m_{1} m_{2}}\right|=\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\)
so that θ = \(\tan ^{-1}\left[\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\right]\)

Question 12.
Find the coordinates of the vertex and focus, and the equations of the directrix and axes of the following parabolas.
(i) y² = 16x
(ii) x² = -4y
(iii) 3x² – 9x + 5y – 2 = 0
(iv) y² – x + 4y + 5 = 0 [Mar. 05]
Solution:
i) y² = 16x, comparing with y² = 4ax,
we get 4a = 16 ⇒ a = 4
The coordinates of the vertex = (0, 0)
The coordinates of the focus = (a, 0) = (4, 0)
Equation of the directrix: x + a = i.e., x + 4 = 0
Axis of the parabola y = 0

ii) x² = -4y, comparing with x² = -4ay,
we get 4a = 4 ⇒ a = 1
The coordinates of the vertex = (0, 0
The coordinates of the focus = (0, -a) = (0, 1)
The equation of the directrix y – a = 0
i.e., y – 1 = 0 .
Equation of the axis x = 0

iii) 3x² – 9x + 5y – 2 = 0
3(x² – 3x) = 2 – 5y
⇒ 3(x² – 2x(\(\frac{3}{2}\)) + \(\frac{9}{4}\)) = 2 – 5y + \(\frac{27}{4}\)
(x – \(\frac{3}{2}\))² = –\(\frac{5}{3}\) (y – \(\frac{7}{4}\)),
Comparing with (x – h)² = -4a (y – k) we get
a = \(\frac{5}{12}\), h = \(\frac{3}{2}\), k = \(\frac{7}{4}\)
∴ Coordinates of the vertex = (h, k)
= (\(\frac{3}{2}\), \(\frac{7}{4 }\))
Coordinates of the focus = (h, k – a)
= (\(\frac{3}{2}\), \(\frac{7}{4}\) – \(\frac{5}{12}\)) = (\(\frac{3}{2}\), \(\frac{4}{3}\))
Equation of the directrix is y – k – a = 0
i.e., 6y – 13 = 0
Equation of the axis is x – h = 0
i.e., 2x – 3 = 0

iv) y² – x + 4y + 5 = 0 ⇒ (y- (-2))² = (x – 1),
comparing with (y – k)² = 4a(x – h),we get
(h, k) = (1, -2) and a = \(\frac{1}{4}\), coordinates of the vertex (h, k) = (1 ,-2)
coordinates of the focus
(h + a, k) = (\(\frac{5}{4}\), -2)
Equation of the directrix x – h + a = 0
i.e., 4x – 3 = 0
Equation of the axis y – k = 0.
i.e., y + 2 = 0

Question 13.
Find the equation of the parabola whose vertex is (3, -2) and focus is (3, 1).
Solution:
The abcissae of the vertex and focus are equal to 3. Hence the axis of the parabola is x = 3, a line parallel to y-axis, focus is above the vertex.
a = distance between focus and vertex = 3.
∴ Equation of the parabola
(x – 3)² = 4(3) (y + 2)
i.e., (x – 3)² = 12(y + 2).

Question 14.
Find the coordinates of the points on the parabola y² = 2x whose focal distance is \(\frac{5}{2}\). [A.P. Mar. 15, Mar. 13]
Solution:
Let P(x₁, y₁) be a point on the parabola
y² = 2x whose focal distance is \(\frac{5}{2}\) then
y₁² = 2x₁ and x₁ + a = \(\frac{5}{2}\)
⇒ x₁ + \(\frac{1}{2}\) = \(\frac{5}{2}\) ⇒ x₁ = 2
∴ y₁² = 2(2) = 4 ⇒ y₁ = ±2
∴ The required points are (2, 2) and (2, -2)

Question 15.
Find the equation of the parabola passing through the points (-1, 2), (1, -1) and (2, 1) and having its axis parallel to the X-axis.
Solution:
Since the axis is parallel to x-axis the equation of the parabola is in the form of
x = -ly² + my + n. .
Since the parabola passes through (-1, 2), we have
-1 = l( 2)² + m(2) + n
⇒ 4l + 2m + n = – 1 ……………………. (1)
Similarly, since the parabola passes through (1,-1) and (2, 1) we have
l – m + n = 1 ……………… (2)
l + m + n = 2 ……………… (3)
Solving (1), (2) and (3)
we get l = –\(\frac{7}{6}\), m = \(\frac{1}{2}\) and n = \(\frac{8}{3}\).
Hence the equation of the parabola is
x = –\(\frac{7}{6}\) y² + \(\frac{1}{2}\) y + \(\frac{8}{3}\) (or)
7y² – 3y + 6x- 16 = 0.

Question 16.
A double ordinate of the curve y² = 4ax is of length 8a. Prove that the line from the vertex to its ends are at right angles.
Solution:
Let P = (at², 2at) and P’ = (at², -2at) be the ends of double ordinate PP’. Then
8a = PP’ = \(\sqrt{0+(4 a t)^{2}}\) = 4at ⇒ t = 2.
∴ P = (4a, 4a), P’= (4a, -4a) .
Slope of \(\overline{\mathrm{AP}}\) × slope of \(\overline{\mathrm{AP}^{\prime}}\)
= (\(\frac{4a}{4a}\))(-\(\frac{4a}{4a}\)) = -1
∴ ∠PAP’ = \(\frac{\pi}{2}\)

Question 17.
i) If the coordinates of the ends of a focal chord of the parabola y² = 4ax are (x₁, y₁) and (x₂, y₂), then prove that x₁x₂ = a², y₁y₂ = -4a².
ii) For a focal chord PQ of the parabola y² = 4ax, if SP = l and SQ = l’ then prove that \(\frac{1}{l}\) + \(\frac{1}{l}\) = \(\frac{1}{a}\).
Solution:
i) Let P(x₁, y₁) = (at₁², 2at₁) and Q(x₂, y₂) = (at₂², 2at₁) be two end points of a focal chord.
P, S, Q are collinear
Slope of \(\overline{\mathrm{PS}}\) = Slope of \(\overline{\mathrm{QS}}\)
\(\frac{2 a t_{1}}{a t_{1}^{2}-a}=\frac{2 a t_{2}}{a t_{2}^{2}-a}\)
t₁t₂² – t₁ = t₂t₁² – t₂
t₁t₂ (t₂ – t₁) + (t₂ – t₁) = 0
1 + t₁t₂ = 0 ⇒ t₁t₂ = -1 ………………… (1)
From (1) x₁x₂ = at₁² at₂² = a²(t₂t₁)² = a²
y₁y₂ = 2at₁2at₂ = 4a²(t₂ t₁) = -4a²

ii) Let P(at₁², 2at₁) and Q(at₂², 2at₁) be the extremities of a focal chord of the parabola, then t₁t₂ = -1 (from (1))

Question 18.
If Q is the foot of the perpendicular from a point P on the parabola y² = 8(x – 3) to its directrix. S is the focus of the parabola and if SPQ is an equilateral triangle then find the length of side of the triangle.
Solution:
Given parabola y² = 8(x – 3) then
its vertex A = (3, 0) and focus = (5, 0)
[4a = 8 ⇒ a = 2] since PQS is an equilateral triangle

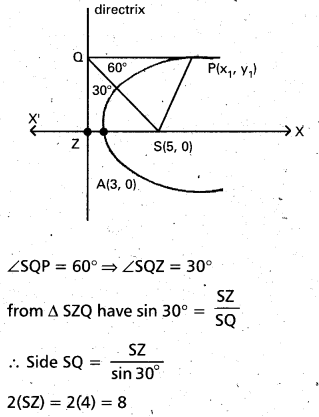
Hence length of each side of triangle is ‘8’.

Question 19.
The cable of a uniformely loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 72 mt. long is supported by vertical wires attached to the cable, the longest being 30 mts. and the shortest being 6 mts. Find the length of the supporting wire attached to the road-way 18 mts. from the middle.

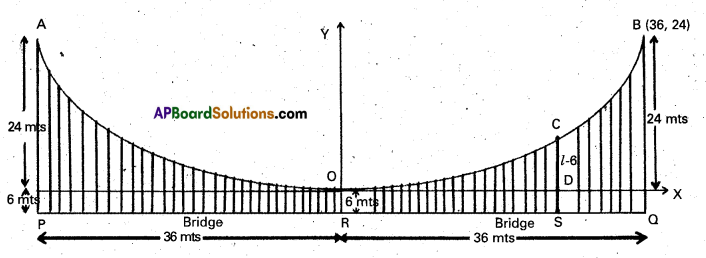
Solution:
Let AOB be the cable [0 is its lowest point and A, B are the highest points]. Let PRQ be the bridge suspended with PR = RQ = 36 mts. (see above Fig.).

PA = QB = 30 mts (longest vertical sup-porting wires)

OR = 6 mts (shortest vertical supporting wire) [the lowest point of the cable is up¬right the mid-point R of the bridge]

Therefore, PR = RQ = 36 mts. We take the origin of coordinates at 0, X-axis along the tangent at O to the cable and the Y-axis along \(\overleftrightarrow{\mathrm{RO}}\). The equation of the cable would, therefore, be x² = 4ay for some a > 0. We get B = (36, 24) and 36² = 4a × 24.
Therefore, 4a = \(\frac{36 \times 36}{24}\) = 54 mts.
If RS = 18 mts. and SC is the vertical through S meeting the cable at C and the X-axis at D, then SC is the length of the supporting wire required. If SC = l mts, then
DC = (l – 6) mts. As such C = (18, l – 6).
Since C is on the cable, 18² = 4a (l – 6)
⇒ l – 6 = \(\frac{18^{2}}{4 a}\) = \(\frac{18 \times 18}{54}\) = 6
⇒ l = 12

Question 20.
Find the condition for the straight line lx + my + n = 0 to be a tangent to the parabola y² = 4ax and find the co-ordinates of the point of contact.
Solution:
Let the line lx + my + n = 0 be a tangent to the parabola y² = 4ax at (at², 2at). Then the equation of the tangent at P(t) is x – yt + at² = 0 then it represents the given line
lx + my + n = 0, then

Question 21.
Show that the straight line 7x + 6y = 13 is a tangent to the parabola y² – 7x – 8y + 14 = 0 and find the point of contact.
Solution:
Equation of the given line is 7x + 6y = 13, equation of the given parabola is y² – 7x – 8y + 14 = 0.
By eliminating x, we get the ordinates of the points of intersection of line and parabola adding the equations y² – 2y + 1 = 0.
i.e., (y – 1 )² = 0 ⇒ y = 1, 1.
∴ The given line is tangent to the given parabola.
If y = 1 then x = 1 hence the point of contact is (1, 1).

Question 22.
Prove that the normal chord at the point other than origin whose ordinate is equal to its abscissa subtends a right angle at the focus.
Solution:
Let the equation of the parabola be
y² = 4ax and P(at², 2at) be any point …………………. (1)
On the parabola for which the abscissa is equal to the ordinate.
i.e., at² = 2at ⇒ t = 0
or t = 2. But t ≠ 0. Hence the point (4a, 4a) at which the normal is
y + 2x = 2a(2) + a(2)³ (or)
y = (12a – 2x) ………………….. (2)
Substituting the value of
y = 12a – 2x in (1) we get
(12a – 2x)² = 4ax (or)
x² – 13ax + 36a² = (x – 4a) (x – 9a) = 0
⇒ x = 4a, 9a
corresponding values of y are 4a and -6a. Hence the other points of intersection of that normal at P(4a, 4a) to the given parabola is Q(9a, -6a), we have S(a, 0).
Slope of the \(\overline{\mathrm{SP}}\) = m₁ = \(\frac{4a-0}{4a-a}\) = \(\frac{4}{3}\),
Slope of the \(\overline{\mathrm{SQ}}\) = m₂ = \(\frac{-6a-0}{9a-a}\) = \(\frac{3}{4}\)
clearly m₁m₂ = -1, so that \(\overline{\mathrm{SP}}\) ⊥ \(\overline{\mathrm{SQ}}\)

Question 23.
From an external point P, tangent are drawn to the parabola y² = 4ax and these tangent make angles θ₁, θ₂ with its axis, such that tan θ₁ + tan θ₂ is constant b. then show that P lies on the line y = bx.
Solution:
Let the coordinates of P be (x₁, y₁) and the equation of the parabola y² = 4ax. Any tangent to .the parabola is y = mx + \(\frac{a}{m}\), if this passes through (x₁, y₁) then
y₁ = mx, + \(\frac{a}{m}\)
i.e., m²x₁ – my₁ + a = 0 ………………… (1)
Let the roots of (1) be m₁, m₂₁.
Then m₁ + m₂ = \(\frac{\mathrm{y}_{1}}{\mathrm{x}_{1}}\)
⇒ tan θ₁ + tan θ₂ = \(\frac{\mathrm{y}_{1}}{\mathrm{x}_{1}}\)
[∵ The tangents make angles θ₁, θ₂ with its axis (x – axis) then their slopes m₁ = tan θ₁ and m₂ = tan θ₂].
∴ b = \(\frac{\mathrm{y}_{1}}{\mathrm{x}_{1}}\) ⇒ y₁ = bx₁
∴ P(x₁, y₁) lies on the line y = bx.

Question 24.
Show that the common tangent to the parabola y² = 4ax and x² = 4by is xa^1/3 + yb^1/3 + a^2/3b^2/3 = 0. [A.P. Mar. 16]
Solution:
The equations of the parabolas are
y² = 4ax ………………. (1)
and x² = 4by …………………. (2)
Equation of any tangent to (1) is of the form
y = mx + \(\frac{a}{m}\)
If the line (3) is a tangent to'(2) also, we must get only one point of intersection of (2) and (3).
Substituting the value of y from (3) in (2),
we get x² = 4b (mx + \(\frac{a}{m}\)) is mx² – 4bm²x – 4ab = 0 should have equal roots therefore its discriminent must be zero. Hence
16b²m⁴ – 4m (-4ab) = 0
16b(bm⁴ + am) = 0
m(bm³ + a) = 0 But m ≠ 0
∴ m = – a^1/3/b^1/3 substituting in (3) the equation of the common tangent becomes
y = \(-\left(\frac{a}{b}\right)^{1 / 3} x+\frac{a}{\left(-\frac{a}{b}\right)^{1 / 3}}\) (or)
∴ a^1/3 x + b^1/3y + a^2/3b^2/3 = 0

Question 25.
Prove that the area of the triangle formed ‘ by the tangents at (x₁, y₁), (x₂, y₂) and (x₃, y₃) to the parabola y² = 4ax (a > 0) is \(\frac{1}{16a}\)|(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units. [T.S. Mar. 15]
Solution:
Let D(x₁, y₁) = (at₁², 2at₁)
E(x₂, y₂) = (at₃², 2at₂)
and F(x₃, y₃) = (at₂³, 2at₃)
be three points on the parabola
y² = 4ax (a > 0).
The equation of the tangents at D, E and F are
t₁y = x + at₁² ………………. (1)
t₂y = x + at₂² ………………. (2)
t₃y = x + at₃² ………………. (3)
(1) – (2) ⇒ (t₁ – t₂) y = a(t₁ – t₂) (t₁ + t₂)
⇒ y = a(t₁ + t₂) substituting in (1)
we get x = at₁t₂
∴ The point of intersection of the tangents at D and E is say P(at₁t₂, a(t₁ + t₂))
Similarly the points of intersection of tangent at E, F and at F, D are Q(at₂t₃, a(t₂ + t₃) and R(at₃t₁, a(t₃ + t₁)) respectively
Area of ∆PQR

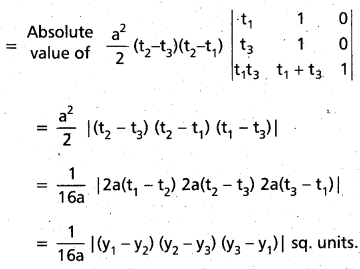
Question 26.
Prove that the two parabolas y² = 4ax and x² = 4by intersect (other than the origin) at an angle of Tan^-1 \(\left[\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\right]\) [Mar. 14]
Solution:
Without loss of generality we assume a > 0 and b > 0.
Let P(x, y) be the point of intersection of the parabolas other than the origin. Then
y⁴ = 16a²x²
= 16a²(4by)
= 64a²by
∴ y[y³ – 64a²b] = 0
⇒ y³ – 64a²b = 0
⇒ y = (64a²b)^1/3 [∵ y > 0]
= 4a^2/3b^1/3

Also from y² = 4ax, x = \(\frac{16 a^{4 / 3} b^{2 / 3}}{4 a}\)
= 4a^1/3b^2/3
∴ P = (4a^1/3b^2/3, 4a^2/3b^1/3)
Differentiating both sides of y² 4ax w.r.t ‘x’, we get
\(\frac{d y}{d x}=\frac{2 a}{y}\)
∴ \(\left[\frac{\mathrm{dy}}{\cdot \mathrm{dx}}\right]_{\mathrm{p}}=\frac{2 \mathrm{a}}{4 \mathrm{a}^{2 / 3} \mathrm{~b}^{1 / 3}}=\frac{1}{2}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{1 / 3}\)
If m₁ be the slope of the tangent at P to y² = 4ax, then
m₁ = \(\frac{1}{2}\left(\frac{a}{b}\right)^{1 / 3}\)
Similarly, we get m₂ = \(2\left(\frac{a}{b}\right)^{1 / 3}\) where m₂ is the slope of the tangent at P to x² = 4by.
If θ is the acute angle between the tangents to the curves at P, then
tan θ = \(\left|\frac{m_{2}-m_{1}}{1+m_{1} m_{2}}\right|=\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\)
so that θ = \(\tan ^{-1}\left[\frac{3 a^{1 / 3} b^{1 / 3}}{2\left(a^{2 / 3}+b^{2 / 3}\right)}\right]\)

Question 27.
Prove that the orthocenter of the triangle formed by any three tangents to a parabola lies on the directrix of the parabola.
Solution:
Let y² = 4ax be the parabola and
A = (at₁², 2at₁),
B = (at₂², 2at₂),
C = (at₃², 2at₃) be any three points on it.
Now we consider the triangle PQR formed by the tangents to the prabola at A, B, C
where P = (at₁t₂, a(t₁ + t₂)),
Q = (at₂t₃, a(t₂ + t₃)) and R = (at₃t₁, a(t₃ + t₁)).
Equation of \(\overleftrightarrow{\mathrm{QR}}\) (i.e., the tangent at C) is x – t₃ y + at₃² = 0.
Therefore, the attitude through P of triangle PQR is
t₃x + y = at₁t₂t₃ + a(t₁ + t₂) ………………….. (1)
Similarly, the attitude through Q is
t₁x + y = at₁t₂t₃ + a(t₂ + t₃) ………………….. (2)
Solving (1) and (2), we get (t₃ – t₁)
x’ = a(t₁ – t₃) i.e., x = – a.
Therefore, the orthocenter of the triangle PQR, with abscissa as -a, lies on the directrix of the parabola.