AP 10th Class Maths Notes 10th Lesson క్షేత్రమితి

Students can go through AP Board 10th Class Maths Notes 10th Lesson క్షేత్రమితి to understand and remember the concept easily.

AP Board 10th Class Maths Notes 10th Lesson క్షేత్రమితి

→ హెరాన్ క్రీ.శ. 10 – క్రీశ. 70 :

• అలెగ్జాండ్రియాకు చెందిన హెరాన్ (క్రీ.శ. 10 – క్రీ.శ. 70) ఒక ప్రాచీన గ్రీకు గణిత శాస్త్రజ్ఞుడు మరియు ఇంజినీర్.
• హెరాన్ వర్గమూలాన్ని దశదశల పద్ధతిలో గణించే పద్ధతిని వర్ణించాడు.
• త్రిభుజ వైశాల్యాన్ని దాని భుజ పొడవుల నుండి కనుగొన్నందుకు ఆయన పేరుతో హెరాన్ ఫార్ములా రూపొందింది. ఇక
• దృక్ శాస్త్రంలో ప్రిన్సిపల్ ఆఫ్ షార్టెస్ట్ పాథ్ ఆఫ్ లైట్’ను హెరాన్ రూపొందించాడు.
• ఆయన వాస్తవ రచనలు మరియు నమూనాలు చాలా వరకు లభ్యమగుట లేదు. అయితే కొన్ని రచనలు అరబిక్ రాత ప్రతులలో భద్రపరచబడినవి.
• ట్యూబ్ నర్ పబ్లిషింగ్ హౌస్ 1903లో లీగ్ లో హెరాన్ ప్రసిద్ధ రచనలను – 5 సంపుటాలుగా వెలువరించింది.

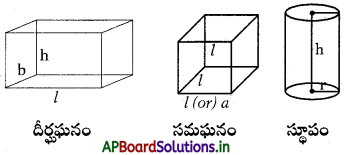
→ మూడు కొలతలు కలిగిన రేఖీయ ఘనాకృతులు ఈ క్రింది విధంగా కలవు.

→ ఘనాకృతులు ఈ క్రింది వైశాల్యాలు కలిగి ఉండును. అవి :

• ప్రక్కతల / ఉపరితల వైశాల్యాలు,
• సంపూర్ణతల వైశాల్యాలు.

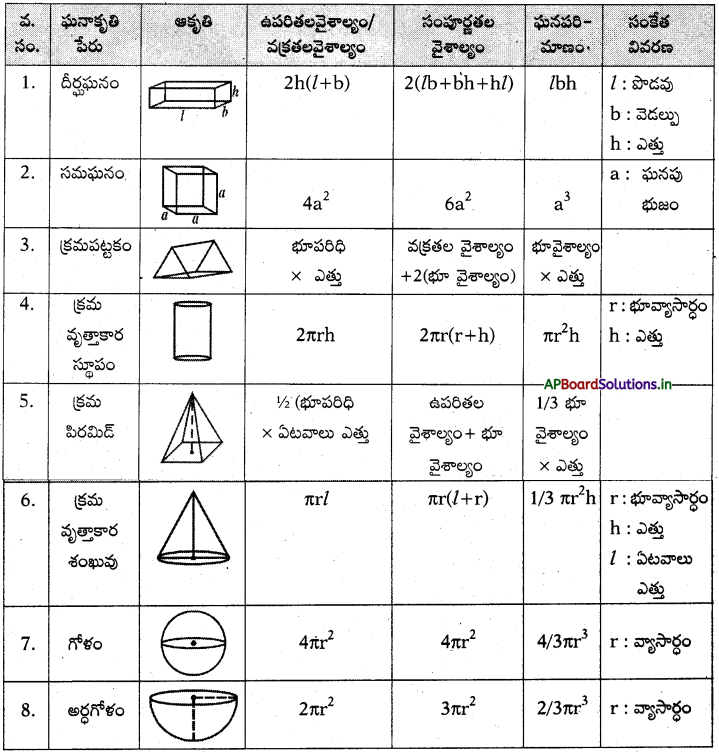
→ దీర్ఘఘనం యొక్క ప్రక్కతల వైశాల్యం = 2h(l + b)
స్థూపం యొక్క ప్రక్కతల వైశాల్యం = 2πrh.

→ స్థూపం యొక్క సంపూర్ణతల వైశాల్యం = స్థూపం యొక్క ప్రక్కతల వైశాల్యం + 2 × భూ వైశాల్యము
= 2πrh + 2πr²- = 2πr(r + h)

సమఘనం యొక్క ఘనపరిమాణం V = a² × a²; V = a³

సూపం యొక్క ఘనపరిమాణం V = πr² × h; V = πr²h.
సూచన : ఘనాకార వస్తు సముదాయ ఉపరితల వైశాల్యము ఆ ఆకృతిలోని ఘనాకార వస్తువుల ఉపరితల వైశాల్యముల మొత్తమునకు సమానము కాదు. దీనికి గల కారణము కొన్ని ఉపరితలములు, వస్తువులను జతపరిచినప్పుడు ఏకీభవిస్తాయి. కనుక వాటిని పరిగణనలోనికి తీసుకోలేము, కాని ఘనపరిమాణము మాత్రము ఆ వస్తువులోని ఘనాకార ఆకృతుల ఘనపరిమాణముల మొత్తమునకు సమానం.

→ వివిధ ఘనాకృతులు, వాటి ఉపరితల వైశాల్యములు, ఘనపరిమాణములు :

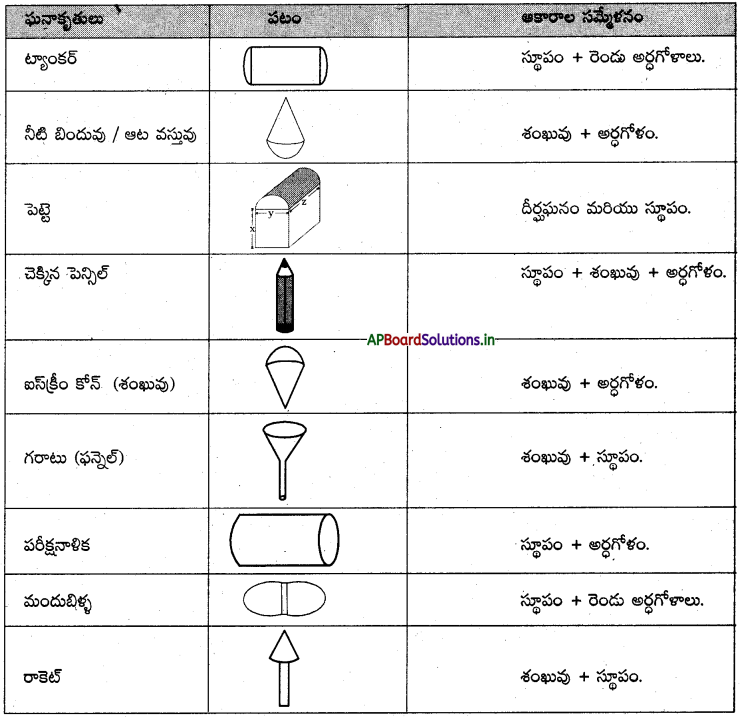
→ కొన్ని ఘనాకృతులు మరియు వాని సమ్మేళన ఆకారాలు :