Students can go through AP Board 10th Class Maths Notes 11th Lesson త్రికోణమితి to understand and remember the concept easily.
AP Board 10th Class Maths Notes 11th Lesson త్రికోణమితి
→ ఆర్యభట్ట 500 A.D:
ఈ రోజుల్లో మనం ఉపయోగించే ‘sine’ అనే భావన యొక్క ఉపయోగం మొట్టమొదటగా 500 A.D. లో ఆర్యభట్ట ద్వారా రాయబడిన “ఆర్యభట్టీయం” లో కనిపిస్తుంది. అందులో ఇది “అర్ధ-జ్యా”గా వాడబడింది. తర్వాత అది “జ్యా”గా లేదా “జివా”గా కాలక్రమేణా మారింది. అరబిక్ భాషలో అనువదింపబడిన ఆర్యభట్టీయంలో “జివా” యొక్క ప్రయోగం కనిపిస్తుంది. తర్వాత లాటిన్ భాషలో అనువదింపబడిన “ఆర్యభట్టీయం” లో “జివా”, “sine (సైన్)”గా మారింది. ఆంగ్ల ఖగోళ శాస్త్ర ఆచార్యుడు ఎడ్మండ్ గుంటర్(1581-1626)మొట్టమొదటగా ‘sine’ ను సూక్ష్మంగా ‘sin’ గా ఉపయోగించాడు.
→ మన నిత్యజీవితంలో వివిధ కట్టడాల ఎత్తులు, దూరాలు మరియు వివిధ సందర్భాల్లో ఏర్పడే కోణాలను త్రిభుజ ధర్మాల ఆధారంగా కనుగొనవచ్చును.
→ ఈ రకమైన సమస్యలను గణితంలో ఒక భాగమైన త్రికోణమితి ఆధారంగా సాధించవచ్చును.
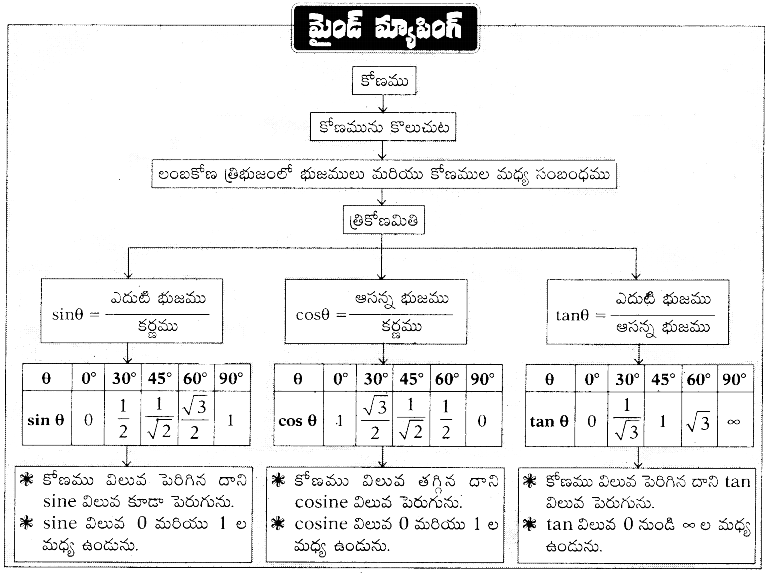
→ త్రికోణమితి అనగా త్రిభుజంలో భుజాలకు మరియు కోణాలకు మధ్యన గల సంబంధంను తెలుపు గణితశాస్త్రము.
![]()
→ లంబకోణ త్రిభుజంలో భుజాలకు పేర్లు పెట్టటం :
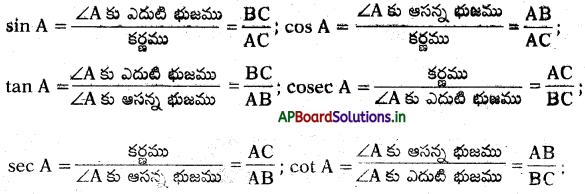
ఒక లంబకోణ త్రిభుజం ABC ని తీసుకొనుము. పటంలో ‘B’ వద్ద లంబకోణము కలదు. A పరంగా ఎదురుగా వున్న భుజము BC కావున దీనిని ∠A కు “ఎదుటి భుజము” గరి అని అంటారు. మిగిలిన భుజము AB ని ∠A కు “ఆసన్న భుజము” అంటారు. ∠B కు ఎదురుగా ఉన్న భుజమును ‘కర్ణము” అంటారు.
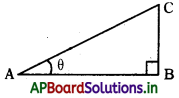
→ త్రికోణమితీయ నిష్పత్తులు : ఒక లంబకోణ త్రిభుజంలో లంబకోణం మినహా మిగిలిన అల్పకోణాలకు, వాటి భుజాలకు మధ్యన గల నిష్పత్తిని “త్రికోణమితీయ నిష్పత్తులు” అంటారు, పటంలో చూపినట్లుగా ‘B’ వద్ద లంబకోణం కలిగిన లంబకోణ త్రిభుజం ABC లో ∠A కు A. త్రికోణమితీయ నిష్పత్తులు

→ “sine A” Dušxomaso as too “cosec A”, sin A : cosec A = 1.
“cosine A” యొక్క గుణకార విలోమం “secant A”, cos A ‘ sec A = 1
“tangent A” యొక్క గుణకార విలోమం “cot A”, tan A . cot A = 1
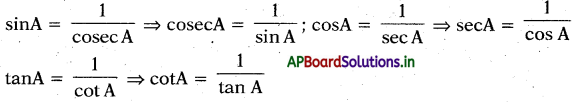
→ త్రికోణమితీయ నిష్పత్తుల యొక్క విలువలు
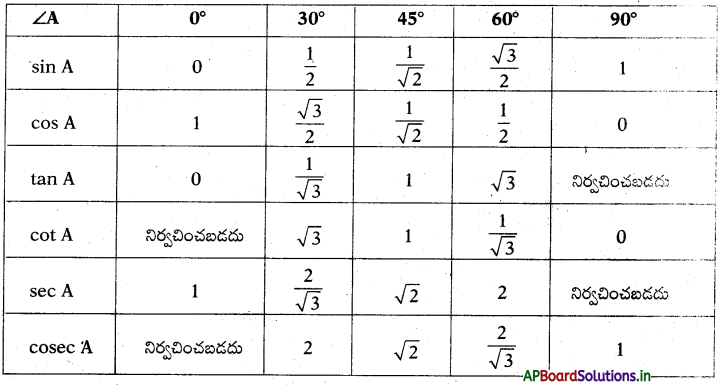
Note: 0 ≤ A ≤ 90 అయిన
- sinA మరియు CosA విలువలు ‘0’ మరియు ‘1’ ల మధ్యన ఉండును.
- tanA విలువ ‘0’ నుండి పెరిగి ‘∞’ అగును.
- cotA విలువ ‘co’ నుండి తగ్గి ‘0’ అగును.
- coseCA విలువ ‘o’ నుండి తగ్గి ‘1’ అగును.
- secA విలువ ‘1’ నుండి పెరిగి ‘∞’ అగును.
- పూరక కోణాల త్రికోణమితీయ నిష్పత్తుల మధ్య సంబంధం :
రెండు కోణాల మొత్తం 90° అయిన వాటిని “పూరక కోణాలు” అంటారు.
→ ఒక లంబకోణ త్రిభుజంలో B వద్ద లంబకోణమున్న ∠A + ∠C = 90° అగును. ∠C = 90° – 2A అగును.
![]()
→ ‘θ’ అల్పకోణమైన sin (90 – θ) = cos θ
- cot (90 – θ) = tanθ
- cos (90 – θ) = sin θ
- sec (90 – θ) = cosec θ
- tan (90 – θ) = cot θ
- cosec (90 – θ) = sec θ అగును
→ కోణమితీయ సర్వసమీకరణం : త్రికోణమితీయ నిష్పత్తుల ఆధారంగా ఏర్పడే అన్ని కోణాలకు సత్యమగు సమీకరణంను “త్రికోణమితీయ సర్వసమీకరణం” అంటారు. .
- sinA + cos- A = 1
- sec – A – tan: A = 1
- cosec – A – cot A = 1
Note : sin2 A = (sinA)2 కాని sinA2 ≠ (sinA)2