Students can go through AP Board 10th Class Maths Notes 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు to understand and remember the concept easily.
AP Board 10th Class Maths Notes 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు
→ థామస్ ఫిస్కీ 15వ శతాబ్దం :
- థామస్ ఫిస్కీ “స్పర్శరేఖ” (Tangent) అను పదాన్ని 1583 సం||లో ప్రవేశ పెట్టాడు .
- ఇతను డెన్మార్క్ దేశస్థుడు.
- టాన్జెంట్ (స్పర్శరేఖ) అను పదం “టాన్ గ్రీ” అను “లాటిన్” పదం నుండి తీసుకొనబడినది.
→ ఒక స్థిర బిందువు నుండి సమాన దూరంలో గల బిందువులను వక్రంచే కలుపగా ఏర్పడిన దానిని ‘వృత్తం’ అంటారు. ఆ స్థిర బిందువును వృత్తానికి కేంద్ర బిందువు అంటారు. దీనిని ‘O’ అను అక్షరంచే సూచిస్తారు.

వృత్తంపై ఏవేని రెండు బిందువులను ఒక రేఖాఖండంచే కలుపగా ఏర్పడు దానిని “జ్యా” అంటారు. వృత్తంలోని అతి పొడవైన జ్యాను “వ్యాసము” అంటారు.
ప్రక్క పటం నుండి
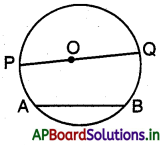
\(\overline{\mathrm{AB}}\) ఒక జ్యా, \(\overline{\mathrm{PQ}}\) వ్యాసము. వృత్త వ్యాసం ఎల్లప్పుడూ కేంద్రం గుండా పోతుంది.
![]()
→ \(\overline{\mathrm{OP}}\) = \(\overline{\mathrm{OQ}}\) = వ్యాసార్థం (r) = \(\frac{d}{2}\) లేదా d = 2r
→ ఒక వృత్తము మరియు రేఖ మధ్య ఈ క్రింది సందర్భాలు కలవు.
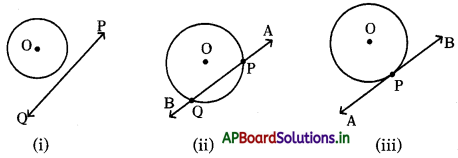
- సందర్భం (i) : (i) వ పటంలో వృత్తానికి, సరళరేఖకు మధ్య ఉమ్మడి బిందువు లేదు. అనగా అవి రెండూ స్పృశించుకొనుటలేదు.
- సందర్భం (ii) : (ii) వ పటంలో \(\overline{\mathrm{AB}}\) అను సరళరేఖ వృత్తాన్ని P, Q బిందువుల వద్ద ఖండిస్తున్నది. కావున \(\overline{\mathrm{AB}}\) సరళరేఖ ఆ వృత్తానికి ఛేదనరేఖ అగును.
- సందర్భం (iii) : (iii) వ పటంలో \(\overline{\mathrm{AB}}\) అను సరళరేఖ వృత్తాన్ని ఒకే ఒక బిందువు P వద్ద తాకుచున్నది. కావున \(\overline{\mathrm{AB}}\) వృత్తానికి ఒక స్పర్శరేఖ అగును.
→ వృత్తానికి ఒక బిందువు వద్ద ఒకే ఒక స్పర్శరేఖ ఉంటుంది.
→ వృత్తానికి గీచిన స్పర్శరేఖకు స్పర్శబిందువు వద్ద దాని వ్యాసార్ధం లంబంగా ఉండును. ”
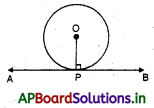
→ స్పర్శరేఖ పొడవు : స్పర్శరేఖ పొడవు AP = \(\sqrt{\mathrm{OP}^{2}-\mathrm{OA}^{2}}\)
OA = వ్యాసార్థం
OP = వృత్తకేంద్రం నుండి బాహ్య బిందువు ‘P’ కు గల దూరం.
→ బాహ్య బిందువు నుండి వృత్తానికి రెండు స్పర్శరేఖలు గీయగలం.
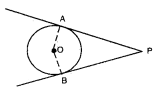
→ బాహ్య బిందువు నుండి వృత్తానికి గీచిన స్పర్శరేఖల పొడవులు సమానాలు. అనగా PA = PB.
→ ‘O’ కేంద్రంగా గల వృత్తానికి ‘P’ అను బాహ్య బిందువు నుండి PA, PB లు గీయబడిన స్పర్శరేఖలు అయిన ∠OPA = ∠OPB.
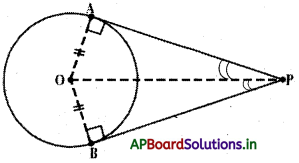
→ ‘O’ కేంద్రంగా గల ఏకకేంద్ర వృత్తాలలో చిన్న వృత్తానికి \(\overline{\mathrm{AB}}\), P వద్ద స్పర్శరేఖ మరియు పెద్ద వృత్తానికి జ్యా అయిన AP = PB అగును.
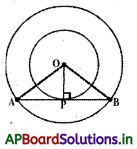
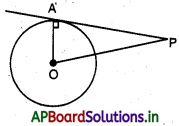
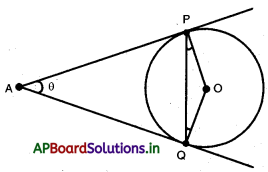
→ పటం నుండి ‘O’ కేంద్రంగా గల వృత్తానికి ‘A’ అను బాహ్య బిందువు నుండి గీయబడిన స్పర్శరేఖలు \(\overline{\mathrm{AP}}\), \(\overline{\mathrm{AQ}}\)లు
అయిన ∠PAQ = 2∠OPQ = 2∠OQP.
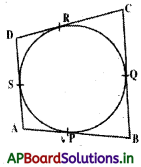
→ ABCD అను చతుర్భుజంలో ఒక వృత్తం అంతర్లిఖించబడినది. ఆ వృత్తం చతుర్భుజాన్ని, P, Q, R, S వద్ద ఖండించినచో AB + CD = BC + DA అగును. అనగా ఎదురెదురు భుజాల మొత్తాలు సమానాలు.
![]()
→ వృత్త ఖండము యొక్క వైశాల్యమును అంచనావేయుటకు వృత్తానికి ఛేదనరేఖలను గీచి వృత్త ఖండాలను ఏర్పరచవచ్చు.
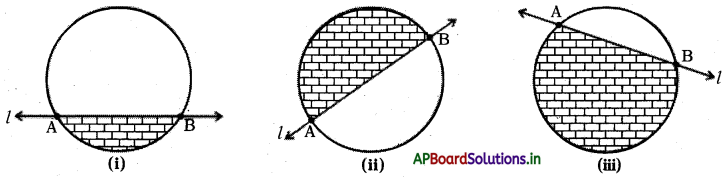
వృత్త చాపము చేతను, జ్యా చేతను ఏర్పడే ప్రదేశమును వృత్త ఖండము అంటారు. దీని వైశాల్యము షేడ్ చేసిన భాగం తెలుపుతుంది. పటము (i) లో అల్ప వృత్తఖండము, పటము (ii) లో అర్ధవృత్తఖండము మరియు పటము (iii) లో అధిక వృత్తఖండము తెలుపుతాయి.
→ ‘O’ కేంద్రంగా గల వృత్తానికి OA, OB లు వ్యాసార్ధాలు (r). x అనునది AB చాపం వృత్తకేంద్రం వద్ద చేయు కోణం అయిన ABP వృత్త ఖండ వైశాల్యం
= AOB సెక్టార్ వైశాల్యం – ∆AOB వైశాల్యం = \(\frac{x}{360}\) – πr² – (\(\frac{1}{2}\)bh).