Students can go through AP Board 10th Class Maths Notes 12th Lesson త్రికోణమితి అనువర్తనాలు to understand and remember the concept easily.
AP Board 10th Class Maths Notes 12th Lesson త్రికోణమితి అనువర్తనాలు
→ వరాహమిహిరుడు (505 – 587)
- మిహిరుడని కూడా పిలవబడే వరాహమిహిరుడు ఉజ్జయినిలో జన్మించిన ఖగోళ శాస్త్రజ్ఞుడు, గణిత మేధావి.
- ఆర్యభట్ట, వరాహమిహిరుల చిత్రపటాలు భారత పార్లమెంటు భవనంలో ఉన్నాయి.
- వరాహమిహిరుడు విక్రమాదిత్య చక్రవర్తి ఆస్థానంలో ఉన్న నవరత్నాలలో ఒకడు.
- 0′ వరాహమిహిరుడు పాస్కల్ త్రిభుజాన్ని కనుక్కొన్నాడు. మాయా చదరాల మీద కృషి చేశాడు. “పంచ సిద్ధాంతిక” (క్రీ.శ. 575) అనే గ్రంథం ఇతని ప్రముఖ రచన.
→ సర్వేయర్లు చాలా వందల యేండ్ల నుండియే త్రికోణమితిని వాడుతూ ఉన్నారు. వారు సర్వే చేసే ప్రక్రియలో ఊర్థ్వకోణం, నిమ్నకోణాలను కనుక్కోవడానికి “థియోడలైట్” అనే పరికరాన్ని వాడతారు. 19వ శతాబ్దంలో “గ్రేట్ ట్రిగనా మెట్రిక్ సర్వే” పేరుతో బ్రిటిష్ ఇండియా భారతదేశంలో సర్వే చేయడానికి రెండు పెద్ద “థియోడలైట్”లను తయారు చేయించింది. ఆ సర్వే జరుగుతుండగా, 1852లో ప్రపంచంలోనే ఒక అతి, పెద్ద పర్వత శిఖరాన్ని భారతదేశంలో కనుగొన్నారు. 160 కి.మీ. దూరం నుండి చుట్టూ ఉన్న ఆరు విభిన్న కూడళ్ల నుండి పరిశీలించి పర్వతం యొక్క ఎత్తును కనుగొన్నారు. 1856లో ఆ సర్వే చేసిన అధికారియైన “సర్ జార్జ్ ఎవరెస్ట్” గౌరవార్థం ఆ శిఖరానికి అతని పేరు పెట్టడం జరిగింది. మొట్టమొదటగా అతడు ఉపయోగించిన ఆ థియోడలైట్లను డెహ్రాడూన్లోని “సర్వే ఆఫ్ ఇండియా మ్యూజియం’లో సందర్శనార్థం పెట్టారు.
→ ఒక వస్తువు యొక్క ఎత్తును గాని, పొడవును గాని కనుగొనడానికి, రెండు వస్తువుల మధ్య దూరాన్ని లెక్కించుటకు త్రికోణమితీయ నిష్పత్తులను వాడుతూ ఉంటాం.
→ త్రికోణమితిని ఉపయోగించేందుకు క్రింది పదములపై అవగాహన అవసరము.
![]()
→ ఆ పదములు దృష్టిరేఖ, క్షితిజ సమాంతర రేఖ, ఊర్థ్వకోణము మరియు నిమ్నకోణములు.
→ క్షితిజ సమాంతర రేఖ : పరిశీలన ‘బిందువు నుండి వస్తువుకు సమాంతరంగా ఉండు రేఖ.
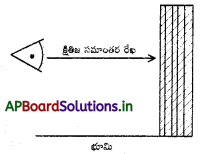
→ దృష్టిరేఖ : పరిశీలకుని కంటి నుండి వస్తువుకి గీయబడిన దృష్టి యొక్క రేఖను “దృష్టిరేఖ” అంటారు.
(లేదా)
ఒక వస్తువుపై ఒక బిందువు నుండి పరిశీలకుని కంటిని కలిపే సరళరేఖ.
→ ఊర్ద్వకోణము : క్షితిజ సమాంతర రేఖకు, దృష్టిరేఖ పైన ఉన్నప్పుడు వాటి మధ్య ఏర్పడే కోణాన్ని “ఊర్ధ్వకోణము” అంటారు. ఈ సందర్భంలో పరిశీలకుడి తల పైకెత్తబడుతుంది.
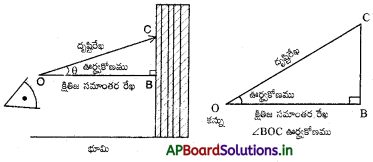
→ నిమ్నకోణము : క్షితిజ సమాంతర రేఖకు, దృష్టిరేఖ ‘క్రింద ఉన్నప్పుడు వాటి మధ్య ఏర్పడే కోణాన్ని “నిమ్నకోణం” అంటారు. ఈ సందర్భంలో పరిశీలకుడి తల క్రింది వైపుకు చూస్తుంది.
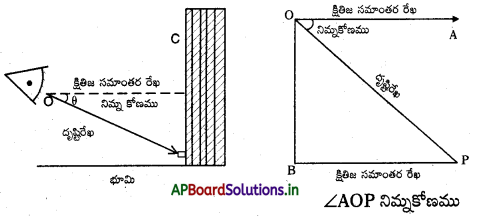
→ గుర్తుంచుకోవలసినవి :
I. లంబకోణ త్రిభుజములో త్రికోణమితీయ నిష్పత్తులు :
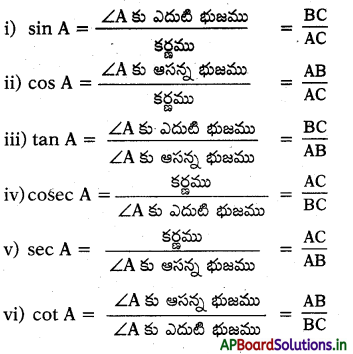
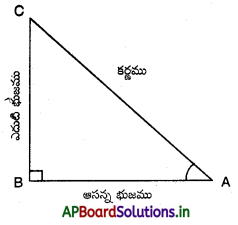
II. కొన్ని త్రికోణమితీయ నిష్పత్తుల విలువలు :
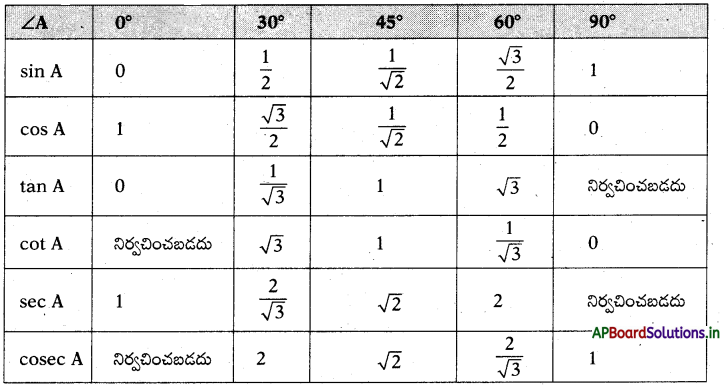
![]()
→ సమస్యల సాధన పద్ధతులు : ఎత్తులు మరియు దూరాలకు సంబంధించిన సమస్యలు సాధించడానికి కింది విషయాలను దృష్టిలో పెట్టుకోవాలి.
- గణితపరంగా సౌలభ్యం కొరకు టవర్లు, చెట్లు, భవనాలు, ఓడలు, పర్వతాలు మొ||లగు వాటిని రేఖీయంగానే పరిగణనలోనికి తీసుకోవాలి.
- ఊర్థ్వకోణం లేదా నిమ్నకోణాన్ని క్షితిజ సమాంతరరేఖ ఆధారంగానే తీసుకోవాలి.
- సమస్యలో పరిశీలిస్తున్న వ్యక్తి ఎత్తు ఇవ్వనట్లైతే, అతడి ఎత్తును లెక్కించకుండానే సమస్యను సాధించాలి.
- ఊర్థ్వ, నిమ్న కోణాలతో ఆ సాధన సందర్భాలను జ్యామితీయంగా ఊహించాల్సి ఉంటుంది.
- సమస్యలను సాధించడానికి వాటికి సంబంధించిన పటాలను గీయడం చాలా ముఖ్యము. వాటి ఆధారంగా సమస్యలను సులభంగా సాధించవచ్చు.