AP 10th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు

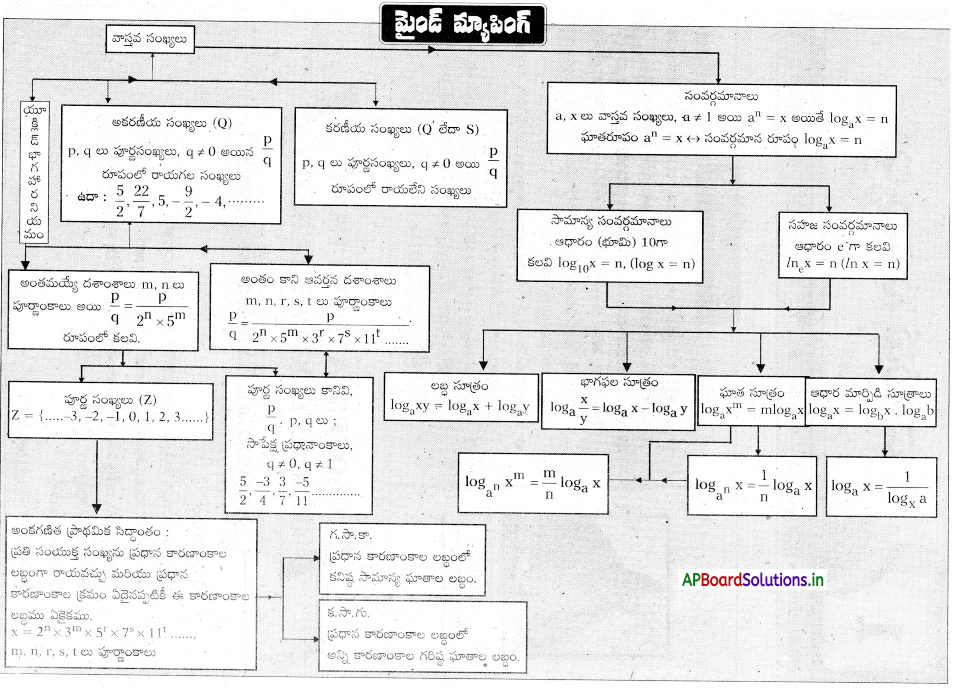
Students can go through AP Board 10th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు

→ యూక్లిడ్ (క్రీ.పూ. 330 – 275):

• యూక్లిడ్ అలెగ్జాండ్రియా రాజు విశ్వవిద్యాలయంలో గణిత బోధకుడిగా పనిచేశాడు. యూక్లిడ్ ను “ఫాదర్ ఆఫ్ జామెట్రీగా” పిలుస్తారు.
• ఇతను అందుబాటులోని గణితాంశాలన్నింటిని సేకరించి, నిర్వచనాలు, స్వీకృతాలు, సిద్ధాంతాలుగా వర్గీకరించి చరిత్ర ప్రసిద్ధి పొందిన గ్రంథం “ఎలిమెంట్స్”ను రచించాడు. ప్రపంచంలో బైబిల్ తర్వాత అత్యధికంగా అమ్ముడు పోయిన గ్రంథం ఇదే.
• యూక్లిడ్ అల్గారిథమ్, సాపేక్ష ప్రధాన సంఖ్యలు, ఒకటి కన్నా పెద్దదైన ఏ పూర్ణ సంఖ్యనైనా ప్రధాన సంఖ్యల లబ్ధంగా ఏకైకం రాయవచ్చు.
• కరణీయ సంఖ్యలు మొదలగునవి ఎలిమెంట్స్ గ్రంథంలోనివే. ఈ నాటికీ పాఠశాలల్లో గణితంగా బోధిస్తున్న దానిలో అధిక భాగం “ఎలిమెంట్స్” ను అనుసరించేవే. యూక్లిడ్ , క్రీ.పూ. 330 – 275

→ వస్తువులను లెక్కించుటకు (count చేయుటకు) అవసరమయ్యే సంఖ్యలను ‘సహజ సంఖ్యలు’ అంటారు. ఈ సంఖ్యా సమితిని N తో సూచిస్తారు. N = {1, 2, 3, ………}

→ గణిత అవసరాలను తీర్చుటకు సహజ సంఖ్య సమితి పూర్తి స్థాయిలో సరిపోవుటలేదనే విషయాన్ని గ్రహించుట ద్వారా “0” (సున్న) ను సహజ సంఖ్యా సమితికి చేర్చుట వల్ల నూతనంగా ఏర్పడే సంఖ్యా సమితిని పూర్ణాంకాలు అంటాం. దీనిని ‘W’ తో సూచిస్తాం. . పూర్ణాంకాలు W = {0, 1, 2, 3, ………….} గణితశాస్త్రానికి “0” సున్నాను పరిచయం చేసినది మన భారతీయులే.

→ సున్నా కంటే తక్కువ విలువ కలిగినవి ఋణపూర్ణాంకాలు. పూర్ణాంకాల సమితి (W) కు ఋణ పూర్ణాంకాలు చేర్చుట ద్వారా ఏర్పడిన సంఖ్యాసమితిని “పూర్ణ సంఖ్యలు” అంటాం. ‘Z’ తో సూచిస్తాం.
Z = {……… -4, -3, -2, -1, 0, 1, 2, 3, …………}

→ పూర్ణ సంఖ్యలు మరియు,” అంతమయ్యే దశాంశాలు, అంతంకాకపోయినా ఆవర్తనమయ్యే దశాంశాలు అన్నింటిని అకరణీయ సంఖ్యలు అంటారు. ఈ అకరణీయ సంఖ్యా సమితిని Q తో సూచిస్తాం. ఈ అకరణీయ సంఖ్యా సమితి పైన చెప్పిన అన్ని సంఖ్యాసమితులు (N, W, Z) కంటే కూడా పెద్ద సంఖ్యా సమితి. ఈ అకరణీయ సంఖ్యలను \(\frac{p}{q}\) రూపంలో వ్రాయగలుగుతాము. p, q లనేవి ‘Z’ కు చెంది ఉంటాయి. q ≠ 0 అవ్వాలి.
Q = {\(\frac{p}{q}\), q ≠ 0; p, q ∈ Z} * అంతములేని, ఆవర్తనముకాని (దశాంశ రూపంలో గల) సంఖ్యలను కరణీయ సంఖ్యలు అంటాం. వీటిని Q’ లేదా S తో సూచిస్తాం. ఉదా : √2, √3, √5, √7 ,………………..

→ కరణీయ సంఖ్యలు, అకరణీయ సంఖ్యలను కలిపి వ్రాయగా ఏర్పడే సంఖ్యాసమితిని వాస్తవసంఖ్యలు అంటాం. దీనిని R తో సూచిస్తాం. R = Q ∪ Q’

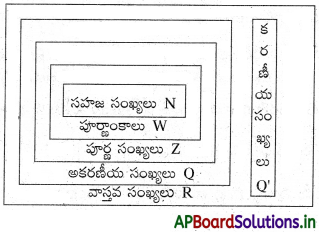
→ ప్రధాన సంఖ్యలు : 1 మరియు అదే సంఖ్య మాత్రమే కారణాంకాలుగా గల 1 కన్నా పెద్దవైన సహజసంఖ్యలు. ఉదా : 2, 3, 5, 7, ………….

→ ప్రధాన సంఖ్య నిర్ధారణ పరీక్ష : p ఒక సంఖ్య మరియు n² > p అయ్యేటట్లు ఉండే కనిష్ఠ సంఖ్య n అయిన n కన్నా చిన్నది లేదా “సమానమైన ఏ ప్రధాన సంఖ్యతోను p భాగింపబడకపోతే p ఒక ప్రధాన సంఖ్య అవుతుంది. ఉదా : 1: 319

• 18² > 319. 18 కన్నా తక్కువైన ప్రధాన సంఖ్యలు 2, 3, 5, 7, 11, 13, 17లలో ఏ సంఖ్యతోను 319 భాగింపబడదు. కావున 319 ప్రధాన సంఖ్య అవుతుంది. ఉదా : 2 : 253
• 16² > 253. 16 కన్నా చిన్నవైన ప్రధాన సంఖ్యలలో ఒకటైన 11 తో 253 భాగింపబడుతుంది.
  ∴ 253 ప్రధానసంఖ్య కాదు.

→ సంయుక్త సంఖ్యలు : 1 మరియు అదే సంఖ్యతోపాటు ఇతర సంఖ్యలతో కూడా భాగింపబడే సహజ సంఖ్యలు.
ఉదా : 4, 6, 9, …………

→ యూక్లిడ్ భాగహార న్యాయము : a = bq + r,0 ≤ r < b అయ్యే విధంగా a మరియు b ల జతకు అనుగుణంగా q మరియు r లు ఏకైక పూర్ణసంఖ్యలు వ్యవస్థితం అవుతాయి. అంకగణిత ప్రాథమిక సిద్ధాంతము : ప్రతి సంయుక్త సంఖ్యను ప్రధాన కారణాంకాల లబ్దంగా రాయవచ్చును మరియు ప్రధాన కారణాంకాల క్రమం ఏదైనప్పటికీ ఈ కారణాంకాల లబ్ధము ఏకైకము.

(i) గ.సా. కా లేదా గ.సా.భా : ఇచ్చిన సంఖ్యల యొక్క సామాన్య ప్రధాన కారణాంకాల యొక్క కనిష్ఠ ఘాతాల లబ్ధం వాని యొక్క గ.సా.5 అగును.
ఉదా : 60, 168 సంఖ్యలను కారణాంకాల లబ్దంగా వ్రాయగా
60 = 22 × 3 × 5; 168 = 22 × 3 × 7
60, 168 ల యందుగల సామాన్య కారణాంకాలు = 2, 3
వాని యొక్క కనిష్ఠ ఘాతాలు = 2², 3¹
∴ 60, 168 ల గ.సా. కా = వాని సామాన్య కారణాంకాల కనిష్ఠ ఘాతాల లబ్దం = 2² × 3 = 4 × 3 = 12

(ii) క.సా.గు : ఇచ్చిన సంఖ్యల యొక్క ప్రతీ ప్రధాన కారణాంకాల గరిష్ఠ ఘాతాల లబ్ధం వాని క.సా.గు (కనిష్ఠ సామాన్య గుణిజం) అగును.
ఉదా : 60, 168 సంఖ్యలను వాని కారణాంకాల లబ్దంగా వ్రాయగా
60 = 2² × 3 × 5; 168 = 2² × 3 × 7
60, 168 గల యొక్క అన్ని ప్రధాన కారణాంకాలు = 2, 3, 5, 7,
వాని యొక్క గరిష్ఠ ఘాతాలు = 2², 3¹, 5¹, 7¹
∴ 60, 168 ల క.సా.గు వాని గరిష్ఠ (ప్రతి కారణాంకం యొక్క ఘాతాల లబ్దం = 2² × 3 × 5 × 7 = 840.

→ ఒక సంఖ్య యొక్క ఒకట్ల స్థానంలో సున్న (0) ఉంటే ఆ సంఖ్య యొక్క ప్రధాన కారణాంకాల లబ్దంలో 2 మరియు 5 ఆ ఉంటాయి. దీని విపర్యయము కూడా నిజము.
ఒక సంఖ్య యొక్క ఒకట్ల స్థానంలో 5 ఉంటే ఆ సంఖ్య యొక్క ప్రధాన కారణాంకాలలో 5 ఉంటుంది.

ఉదా :

• 510 = 2 × 5 × 3 × 17;
• 620 = 2² × 5 × 31;
• 45 = 3² × 5;
• 455 = 5 × 7 × 13

→ x అనేది ఒక అకరణీయ సంఖ్య మరియు దీని దశాంశ రూపం ఒక అంతమయ్యే దశాంశము అయినప్పుడు x ను p, q లు పరస్పర ప్రధానాంకాలు అయివున్న \(\frac{p}{q}\) రూపంలో వ్యక్తపరచవచ్చు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్దం 20 5m అవుతుంది. ఇందులో n, m లు రుణేతర పూర్ణసంఖ్యలు. దీని విపర్యయము కూడా నిజము. విపర్యయము : ‘n, m లు రుణేతర పూర్ణసంఖ్యలు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్ధరూపం 215m కలిగినటువంటి అకరణీయ సంఖ్య x = \(\frac{p}{q}\) అయిన X యొక్క దశాంశ రూపం ఒక అంతమయ్యే దశాంశం అవుతుంది. (p, q లు సాపేక్ష ప్రధాన సంఖ్యలు)

→ x ఒక అకరణీయ సంఖ్య, p, q లు సాపేక్ష ప్రధాన సంఖ్యలు అయి x = \(\frac{p}{q}\) అంతమవు దశాంశము అయితే q = 2ⁿg^m రూపంలో ఉంటుంది. ఈ దశాంశము n, m లలో పెద్దదైన సంఖ్యకు సమానమైన అంకెల వద్ద అంతం అవుతుంది.

ఉదా : \(\frac{13}{40}=\frac{13}{2^{3} \times 5}\) ; n = 3, m = 1 మరియు n > m.
\(\frac{13}{40}\) మూడు దశాంశాల తర్వాత అంతం అవుతుంది. ..
\(\frac{13}{40}\) = 0.325

→ n, m లు రుణేతర పూర్ణసంఖ్యలు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్దము 2ⁿg^m రూపంలో లేకుంటే అకరణీయ సంఖ్య x = \(\frac{p}{q}\) యొక్క దశాంశ రూపం ఒక అంతంకాని.ఆవర్తన దశాంశము అవుతుంది.

→ p అనేది ఒక ప్రధాన సంఖ్య మరియు a ఒక ధనపూర్ణ సంఖ్య అయితే a² ను p నిశ్శేషంగా భాగిస్తే, a ను p నిశ్శేషంగా
భాగిస్తుంది. సంవర్గమానాలు : a మరియు N లు ధన పూర్ణసంఖ్యలై a > 1, N > 0 అవుతూ a^x = N అయిన దీనిని సంవర్గమాన రూపంలో log_a N = x అని వ్రాస్తాము. ఇచ్చట a, N ∈ R

గమనిక : ధన పూర్ణసంఖ్యలకు మాత్రమే సంవర్గమానాలు నిర్వచించబడ్డాయి.

• log_a 1 = 0 (ఏ ఆధారానికైనా 1 యొక్క సంవర్గమానం ‘0’.)
• log_a = 1

→ ఒక సంఖ్య యొక్క సంవర్గమానాలు విభిన్న భూములకు (ఆధారాలకు) వేర్వేరుగా ఉంటాయి.
ఉదా :

• 64 = 8² యొక్క సంవర్గమాన రూపం log₈ 64 = 2
• 64 = 4³ యొక్క సంవర్గమాన రూపం log₄ 64 = 3
• 64 = 2⁶ యొక్క సంవర్గమాన రూపం log₂ 64 = 6

→ సంవర్గమాన న్యాయాలు : లబ్ధ సూత్రం

• log_a xy = log_ax + log_ay భాగఫల సూత్రం
• log_a \(\frac{x}{y}\) = log_ax – log_ay

→ ఘాత సూత్రాలు :

• log_a x^m = m log_a x,
• log_aⁿ n x = \(\frac{1}{n}\) log_a x;
• log_aⁿ n x^m = \(\frac{m}{n}\) log_a x
• a log_a x = x

→ ఆధార మార్పిడి సూత్రాలు :

• log_ax = log_bx. log_ab;
• log_ax = \(\frac{1}{\log _{x} a}\)

→ సంఖ్యల సంవర్గమానాలు పూర్ణాంక, దశాంశ భాగాలను కలిగి ఉంటాయి. పూర్ణాంక భాగాన్ని లాక్షణిక అని, దశాంశ భాగాన్ని మాంటిస్సా అని అంటారు.
ఒక అంకె సంఖ్య సంవర్గమానాల లాక్షణిక సున్న.
రెండు అంకెల సంఖ్య సంవర్గమానాల లాక్షణిక 1.
– మూడు అంకెల సంఖ్య సంవర్గమానాల లాక్షణిక 2.

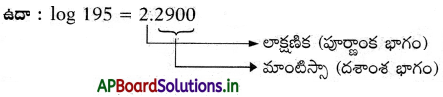
→ ఒక సంఖ్యలో n అంకెలుంటే ఆ సంఖ్య యొక్క లాక్షణికలో (n- 1) అంకెలుంటాయి. విపర్యయంగా, ఒక సంవర్గమాన లాక్షణిక n అయిన, ఆ సంఖ్యలో (n + 1) అంకెలుంటాయి.

ఉదా : ఒక తేనెటీగల గుంపు రెండు పువ్వులపై సమాన సంఖ్యలో వాలినపుడు ఒక తేనెటీగ మిగులుతుంది. అదే గుంపు మూడు పూవులపై సమాన సంఖ్యలో వాలినపుడు రెండు తేనెటీగలు మిగులుతాయి. అదే గుంపు నాలుగు పూవులపై సమాన సంఖ్యలో వాలినపుడు 3 మిగులుతాయి. అదే గుంపు ఐదు పూవులపై సమాన సంఖ్యలో వాలినపుడు మరి మిగలవు. ఆ గుంపులో గరిష్టంగా 50 వరకు తేనెటీగలు కలిగి ఉండవచ్చు. అయిన వాటి ఖచ్చిత సంఖ్య కనుగొనుము.

→ సాధన. ఈ గుంపులో గల తేనెటీగలు = x అనుకుందాం
రెండు పూవులపై సమానంగా వాలిన 1 మిగులును

• కావున x = 2a + 1 గా వ్రాయవచ్చును. ……………………….(1)
• మూడు పూవులపై సమానంగా వాలిన 2 తేనెటీగలు మిగులును. కావున x = 3b + 2 ………………(2)
• నాలుగు పూవులపై సమానంగా వాలిన 3 తేనెటీగలు మిగులును. కావున x = 4c + 3.0 ……………….(3)
• ఐదు పూవులపై సమాన సంఖ్యలో వాలిన మరి మిగలవు. కావున x = 5d + 0 ……………..(4)

మరియు x ≤ 50 (ఎందుకనగా అవి గరిష్ఠంగా 50)
x అనునది 5 గుణజం అని 4వ సమీకరణం నుండి అర్థమగును కావున x యొక్క సాధ్య విలువలు = 5, 10, 15, 20, 25, 30, 35, 40 మరియు 45. మొదటి సమీకరణం నుండి x బేసి సంఖ్య అని అర్థమగును. కావున ఇపుడు ‘x’ యొక్క సాధ్య విలువలు = 5, 15, 25, 35, 45 (పై వాటి నుండి సరిసంఖ్యలు తొలగించాం). సమీకరణ (2) ప్రకారం 3చే భాగిస్తే శేషం 2 రావాలి.

కావున ఇపుడు ‘x’ యొక్క సాధ్య విలువలు = (5, 35). సమీకరణ (3) ప్రకారం 4చే భాగిస్తే శేషం 3 రావాలి. కావున 5, 35 లలో 35 మాత్రమే 4 చే భాగించినపుడు 3 శేషాన్ని ఇవ్వగలుగుతుంది.
∴ ఆ గుంపులో 35 తేనెటీగలు కలవని అర్థమవుచున్నది.

సరిచూచుట :

• 35 తేనెటీగలు 5 పూవుల పై వాలిన \(\frac{35}{5}\) = 7 (శేషం – 0)
• 35 తేనెటీగలు 4 పూవుల పై వాలిన \(\frac{35}{4}\) = 8 (శేషం – 3)
• 35 తేనెటీగలు 3 పూవులపై వాలిన \(\frac{35}{3}\) =11 (శేషం – 2)
• 35 తేనెటీగలు 2 పూవులపై వాలిన \(\frac{35}{2}\) =17 (శేషం – 1)