AP 10th Class Maths Notes 3rd Lesson బహుపదులు

Students can go through AP Board 10th Class Maths Notes 3rd Lesson బహుపదులు to understand and remember the concept easily.

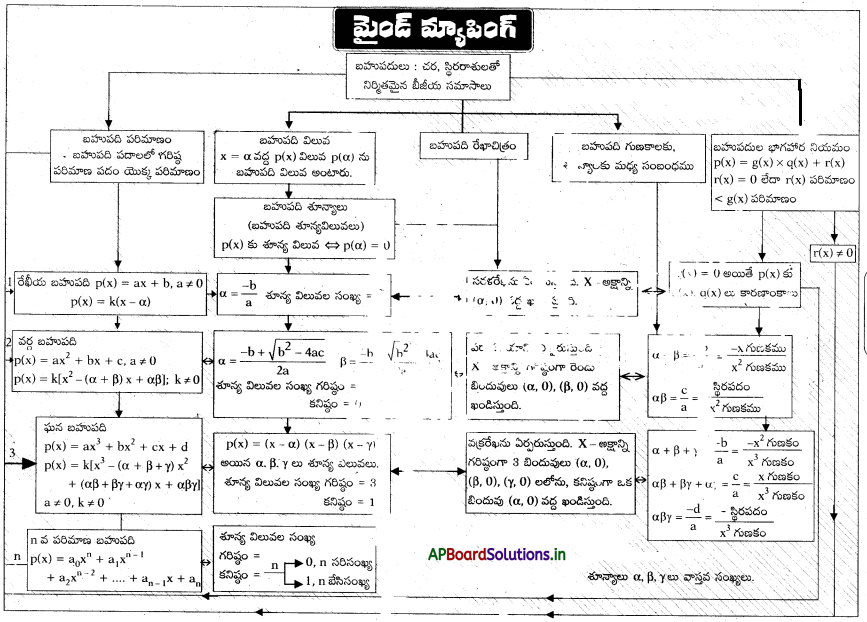
AP Board 10th Class Maths Notes 3rd Lesson బహుపదులు

→ పావులూరి మల్లన 11వ శతాబ్దం :

• పావులూరి మల్లన ప్రముఖ గణిత శాస్త్రజ్ఞుడు. ఇతడు 11వ శతాబ్దానికి చెందిన తూర్పు .
• చాళుక్యరాజైన రాజరాజనరేంద్రుని ఆస్థాన పండితుడు. ఇతను నన్నయ భట్టుకు సమకాలికుడు.
• పావులూరి మల్లన మహావీరాచార్యునిచే రచింపబడిన ‘గణితసార సంగ్రహం’ అనే ఆ సంస్కృత భాషలోని గణితగ్రంథాన్ని స్వతంత్ర అనువాద పద్దతిలో తెలుగు భాషలోకి అనువదించాడు. దీని పేరు “సారసంగ్రహ గణితం”. చాలా సరళమైన శైలిలోని ఈ గణిత గ్రంథము ఒక పద్యకావ్యంలా ఉంటుంది. ఆ కాలం ఆ మూల గంథమైన ‘గణిత సారసంగ్రహం ‘లో పరికర్మ, భిన్న, ప్రకీర్ల, తైరాశిక, మిత్ర క్షేత్ర, ఖాత, ఛాయవ్యవహారములు అని 8 ప్రకరణాలుగా ఉంటే మల్లన మిశ్ర గణితాన్ని సూత్ర గణితం, సువర్ణ గణితం అని రెండు భాగాలుగా చేశాడు.
• మూలములోని గణిత విధానములను మాత్రమే తీసుకొని సమస్యలు, ఉదాహరణలు, తనదైన పద్ధతిలో స్వతంత్రముగా ఇచ్చాడు. భిన్నాంకముల సమస్యలలో ‘ఇష్టకర్మము’ , అనే గణిత వ్యవహారంలో కూడా మల్లన అనేకమైన ఉదాహరణలు ఇచ్చాడు.
• సార సంగ్రహ గణితం’ గ్రంధాన్ని పాటి గణితం, క్షేత్ర గణితం మరియు బీజ గణితం – అనే మూడు విభాగాలుగా వ్రాశాడు. పావులూరి గణితంగా ప్రసిద్ది చెందిన “సార సంగ్రహగణితం” తొలి తెలుగు గ్రంథం. తొలి తెలుగు గణిత గ్రంథం వ్రాసిన ఘనత – పావులూరి మల్లనకు దక్కింది.

→ బహుపది . చరరాశుల యొక్క ఘాతాంకాలు రుణేతర పూర్ణసంఖ్యలుగా గల బీజీయ సమాసాలను ‘బహుపదులు అంటారు.

ఉదా :

• 3x + 9
• 4x²y + 3xy² – 7xy + 7
• x³ – √3 x² + 7x – 9

→ బహుపది పరిమాణం : బహుపది వివిధ పరిమాణాలలో గరిష్ఠ పరిమాణమే బహుపది పరిమాణము.
ఉదా : p(x) = 7x⁴ – 3×3 + 5×2 + 9x + 3 యొక్క పరిమాణం :  4
ply) = 9×3 – 7×5 – 8 + 7×2 – Q యొక్క పరినూణం : 5

సూచన : p(x) ఒక బహుపది అయిన X యొక్క గరిష్ఠ ఘాతాంకము p(x) యొక్క పరిమాణం అవుతుంది.

→ n వ పరిమాణ బహుపది యొక్క సాధారణ రూపం :
p(x) = a₀xⁿ + a₁ x^n-1 + a₂ x^n-2 + …. + a_n-1 x + a_n. ఇక్కడ a₀, a₁, a₂, . . a_n-1, a లు వాస్తవ సంఖ్యలు మరియు a₀ ≠ 0.

• స్థిర బహుపది : ‘సున్న’ పరిమాణంగా గల బహుపది
  ఉదా : p(x) = 8
  p(y) = – 4 .
• రేఖీయ బహుపది : పరిమాణం ‘1’ గా గల బహుపది
  ఉదా : p(x) = 5x – 4
  p(x) = 9z + 27 .
• వర్గ బహుపది : పరిమాణం ‘2’ గా గల బహుపది
  ఉదా : p(x) = x² + 5x + 6 .
  p(y) = 4y² – 12y + 9
• ఘన బహుపది : పరిమాణం ‘3’ గా గల బహుపది
  ఉదా : p(x) = 8x³ – 4x² + 9x + 8
  p(y) = y³ + 8y² – 3y + 4

సూచన : బహుపది యొక్క పరిమాణం ఆ బహుపదిలోని పదాలకన్నా 1 తక్కువ p(x) లో n పదాలు ఉంటే p(x) యొక్క పరిమాణం : n – 1.

→ బహుపది విలువ : బహుపది p(x) లోని చరరాశి x కు k ను ప్రతిక్షేపించగా వచ్చే విలువను x = k వద్ద p(x) యొక్క బహుపది విలువ అంటారు. దీనిని p(k) తో సూచిస్తారు.
ఉదా : p(x) = x² – 5x + 6
x = 1 వద్ద p(x) విలువ
p(1) = (1)² 5 (1) + 6
= 1 – 5 + 6 = 2
x = 1 వద్ద p(x) విలువ p(1) = 2

→ బహుపది శూన్య విలువ : బహుపది p(x) లోని చరరాశి x యొక్క ఏ విలువకు p(x) బహుపది విలువ శూన్యం (‘0’) అవుతుందో. x యొక్క ఆ విలువను బహుపది p(x) శూన్య విలువ అంటారు
ఉదా :

(1) p(x) = 5x – 10
x = 2 అయిన p(2) = 5(2)
10 = 10
10 = 0
p(2) = 0
కావున p(x) = 5x
10 యొక్క శూన్య విలువ ‘2’ అవుతుండ

(2) p(x) = x² – 3x + 2
x = 3 అయిన
p(3) = (3)² – 3(3) + 2 = 2
p(3) = 2
p(3) ≠ 0 కావున p(x) కు 3 శూన్య విలువ కాదు.

(1) రేఖీయ బహుపది p(x) = ax + b ఒకే ఒక శూన్య విలువ x =-b/a ను కలిగి ఉంటుంది.

(2) (i) వర్గ బహుపది p(x) = ax² + bx + c గరిష్ఠంగా రెండు శూన్య విలువలను కలిగి ఉంటుంది.
(ii) p(x) = ax² + bx + c వర్ణ బహుపది కావున

• D = b² – 4ac > 0 అయిన రెండు శూన్య విలువలు (α ≠ β), α, β ∈ R ను కలిగి ఉంటుంది.
• D = b² – 4ac = 0 అయిన ఒకే ఒక శూన్య విలువ (α = β), α ∈ R ను కలిగి ఉంటుంది.
• D = b² – 4ac < 0 అయినప్పుడు p(x) కు వాస్తవ శూన్య విలువలు ఉండవు.

(iii) వర్గ బహుపది p(x) యొక్క శూన్య విలువలు

• D = b² – 4ac > 0 అయినప్పుడు α ≠ β
  α = \(\frac{-b+\sqrt{D}}{2 a}\) మరియు β = \(\frac{-b-\sqrt{D}}{2 a}\)
• D = b² – 4ac = 0 అయినప్పుడు α = β
  α = \(\frac{-b}{2 a}\)

(3) ఘన బహుపది p(x) = ax³ + bx² + cx + d గరిష్ఠంగా 3 శూన్య విలువలను కలిగి ఉంటుంది.

(4) 1వ పరిమాణ బహుపది గరిష్ఠంగా n శూన్య విలువలను కలిగి ఉంటుంది.

→ బహుపదులను రేఖీయ చిత్రాలుగా చూపడం :

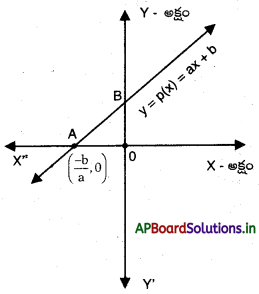
• రేఖీయ బహుపది p(x) = ax + bని జ్యా మితీయంగా చిత్రించినపుడు ‘వచ్చే గ్రాఫ్ ఒక సరళరేఖను సూచిస్తుంది.
  y = p(x) = ax + b, a ≠ 0 గ్రాఫ్ సూచించే సరళరేఖ
  X – అక్షాన్ని ఒకే ఒక బిందువు ( \(\frac{-b}{a}\), 0) వద్ద ఖండిస్తుంది. ఈ ఖండన బిందువులోని X – నిరూపకం \(\frac{-b}{a}\), p(x) = ax + b యొక్క శూన్య విలువ అవుతుంది.
• వర్గ బహుపది y = p(x) = ax² + bx + c రేఖీయ చిత్రం ఒక పరావలయాన్ని సూచిస్తుంది. p(x) లో x² గుణకం a > 0 అయిన పరావలయం పైవైపు వివృతంగాను a < 0 అయిన క్రిందివైపు వివృతంగాను ( ) ఉంటుంది. ఈ రెండు రకాల పరావలయాలు X – అక్షాన్ని గరిష్ఠంగా రెండు బిందువుల వద్ద ఖండిస్తాయి. ఈ రెండు బిందువులలోని X – నిరూపకాలే p(x) యొక్క శూన్య విలువలు అవుతాయి.

సూచన :
p(x) = ax² + bx + c, X- అక్షాన్ని (\(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\), 0) మరియు (\(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\), o) అనే బిందువుల వద్ద ఖండిస్తుంది.

→ ఘన బహుపది : ఘన బహుపది p(x) = ax³ + bx² + cx + d రేఖాచిత్రం X – అక్షాన్ని గరిష్టంగా మూడు బిందువుల వద్ద ఖండిస్తుంది. ఈ మూడు బిందువులలోని X- నిరూపకాలు p(x) యొక్క శూన్య విలువలు అవుతాయి.

→ ఘన బహుపది రేఖాచిత్రము – వివిధ సందర్భాలలో : p(x) = ax³ + bx² + cx + d:

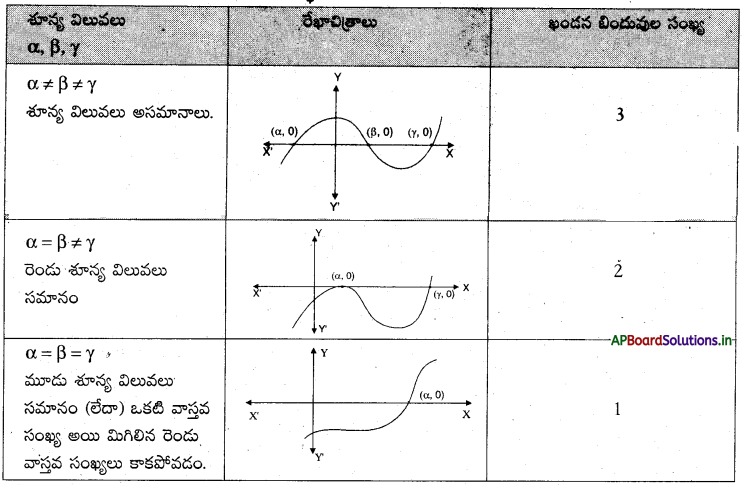
→ బహుపదుల భాగహార అల్ గారిథమ్ (బహుపదుల భాగహార నియమం) : p(x) మరియు g(x) లు రెండు బహుపదులు, g(x) = 0 అయిన p(x) = g(x) × q(x) + r(x) అయ్యేటట్లు q(x) మరియు r(x) అనే బహుపదులను కనుగొనవచ్చును. ఈ ఫలితాన్నే ‘బహుపదుల భాగహార అల్గారిథమ్’ అంటారు. ఇక్కడ r(x) = 0 లేదా r(x) పరిమాణం < g(x) పరిమాణం .

పై నియమం నుండి మనం క్రింది విషయాలు తెలుసుకొనవచ్చును.

• g(x) రేఖీయ బహుపది అయితే r(x) = స్థిరాంకము.
• q(x) పరిమాణం 1 అయిన p(x) పరిమాణం = 1 + g(x) పరిమాణం.
• q{x} పరిమాణం n అయిన p(x) పరిమాణం = n + g(x) పరిమాణం
• p(x) ను X – a చే భాగించగా వచ్చే శేషము p(a) అవుతుంది.
• శేషము r = 0 అయితే p(x) కు g(x) కారణాంకము అవుతుంది.
  అనగా p(x) = g(x) × q(x) అవుతుంది.