AP 10th Class Maths Notes 7th Lesson నిరూపక రేఖాగణితం

Students can go through AP Board 10th Class Maths Notes 7th Lesson నిరూపక రేఖాగణితం to understand and remember the concept easily.

AP Board 10th Class Maths Notes 7th Lesson నిరూపక రేఖాగణితం

→ రెనె డెకార్టి (1596 – 1650)

• గణిత శాస్త్రవేత్త ఆ రెనె డెకార్టె 31-3-1596వ తేదీన ఫ్రాన్లోని లాహై నగరంలో ఒక ఆ సామాన్య కుటుంబంలో జన్మించాడు. ఆధునిక గణితానికి, తత్వ శాస్త్రానికి పితామహునిగా పేరొందాడు.
• విశ్వసనీయమైన జ్ఞానాన్నిచ్చే నూతన పద్దతి కోసం అన్వేషణ, విశ్వ పునర్నిర్మాణానికి కృషి చేశాడు. గణిత పద్దతులను అధ్యయనం చేసి, వాటి నుంచి పరిశుద్ధమైన జ్ఞానాన్ని అన్ని క్షేత్రాలలో రూపొందించే పద్ధతిగా “విశ్వగణితాన్ని” ఆవిష్కరించేందుకు కొన్ని సార్వత్రిక నియమాల అన్వేషణ రెనె డెకార్ట్ సాగించాడు. 1596-1650
• తలంలోని బిందువులను వాస్తవ సంఖ్యా క్రమయుగ్మాలతో అనుసంధానం చేయడం వల్ల రేఖాగణితానికి, బీజగణితానికి మధ్య అంతరం పోయి రెండింటిని కలిపి ఒకటిగానే అధ్యయనం చేయడం సాధ్యమైనది.
• రేఖాగణిత, బీజగణితాలను ఏకం చేసే ప్రయత్నంలో నిరూపక రేఖాగణితం లేదా వైశ్లేషిక జ్యామితి అనే గణిత శాఖకు మూల పురుషుడయ్యాడు. ఇతని గౌరవార్థం ఈ శాఖకు కార్టీజియన్ రేఖాగణితం అని పేరు పెట్టారు.
• తత్వశాస్త్రం, జ్యామెట్రీ, డయాప్టిక్స్ అనే మూడు అంశాల వ్యాస సంపుటిగా “దిస్ కో ఆన్ మెథడ్” అనే ప్రసిద్ధ గ్రంథాన్ని రచించాడు. వర్గమూలానికి మొదటిసారిగా ‘ √ ‘ గుర్తును ఉపయోగించాడు.
• డెకార్టెతత్వ శాస్త్రానికి, వైశ్లేషిక రేఖా గణితానికి ప్రజాదరణ పెరగడంతో హాలెండ్ రాజు డెకార్టెను ఆహ్వానించి యువరాణి క్రిష్టినాకు బోధకునిగా నియమించాడు. ఆమె దినచర్య కారణంగా ఉదయం 5 గం||లకే చలిలో డెకార్టెరాజ ప్రాసాదానికి వెళ్ళవలసి వచ్చేది. ఆ వాతావరణం పడక న్యుమోనియా వ్యాధికి గురై 54 ఏళ్ళ వయస్సులో 11-2-1650వ తేదీన మరణించాడు.
• “సత్యాన్వేషణ కోసం మనం జీవితంలో ఒకసారి అన్నింటిని శంకించవలసి వస్తుంది”.. అంకు – రెనె డెకార్టి

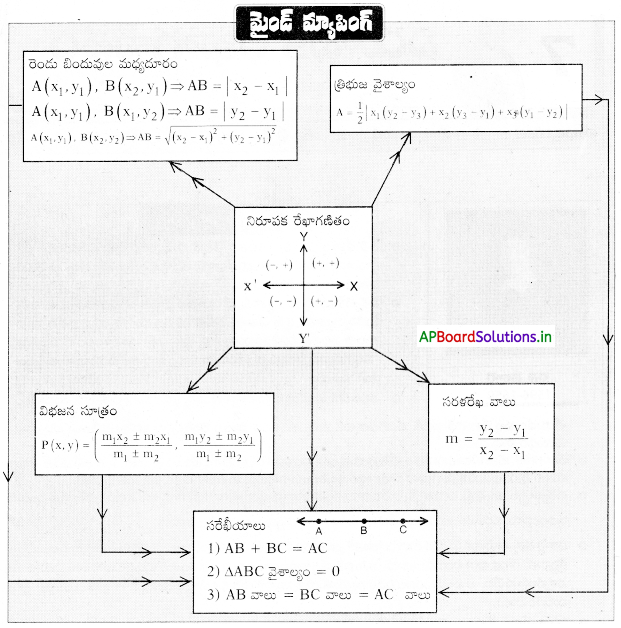
→ ఒకే తలంలో గల క్షితిజ సమాంతర మరియు క్షితిజ లంబరేఖలు ఆ తలాన్ని నాలుగు భాగాలుగా విభజిస్తాయి. క్షితిజ సమాంతరరేఖను X – అక్షం అని, క్షితిజ లంబరేఖను Y – అక్షం అని, ఈ రెండు రేఖల ఖండన బిందువును మూలబిందువు అని అంటారు.

→ X, Y అక్షాలతో ఏర్పడిన నాలుగు భాగాలను వరుసగా 1వ పాదం (Q₁), 2వ పాదం (Q₂), 3వ పాదం (Q₃), 4వ పాదం (Q₄)లుగా పిలుస్తారు. ఈ తలాన్ని ‘కార్టిజియన్ తలం’ (రెనెడెకార్ట్ పేరుతో) లేదా నిరూపక | x < 0, y < 0 1 x > 0, y < 0. తలం లేదా XY తలం అని అంటారు.

→ నిరూపక తలంలోని రెండు బిందువుల మధ్య దూరం :
(i) నిరూపక అక్షాలకు సమాంతరంగా ఉన్న రేఖ పైగల రెండు బిందువుల మధ్య దూరం :
(a) X – అక్షానికి సమాంతరంగా గల రేఖ పై గల బిందువులలో y – నిరూపకాలు సమానంగా ఉంటాయి.
A(x₁, y₁) B (x₂, y₂) లు X – అక్షానికి సమాంతరంగా గల రేఖపై గల బిందువులు అవుతాయి.
A, B ల మధ్య దూరం = |x₂ – x₁| అనగా వాని X – నిరూపకాల మధ్య వ్యత్యాసమునకు సమానము.

(b) ఇదే విధంగా A(x₁, y₁), B(x₂, y₂) లు Y – అక్షానికి సమాంతరంగా గల రేఖ పై బిందువులు అవుతాయి. ఆ
A, B ల మధ్య దూరం = |y₂ – Y₁| అనగా Y నిరూపకాల మధ్య తేడాకు సమానము.

(ii) నిరూపక తలంలోని ఏవేని రెండు బిందువుల మధ్య దూరం :

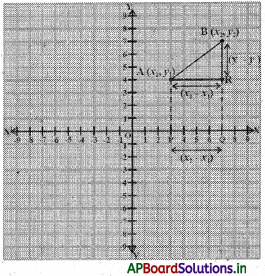
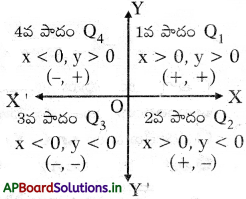
A(x₁, y₁) B (x₂, y₂) లు నిరూపక తలంలో రెండు బిందువులు అనుకొందాం.
OP = x₁ OQ = x₂ అలాగే QB = y₂, QR = y₁
∴ PQ = AR = x₂ – x₁ ……………(1)
ఇదే విధంగా, BR = y₂ – y₁ …………….(2)
∆ARB ఒక లంబకోణ త్రిభుజము.
AB² = AR² + RB² (పైథాగరస్ సిద్ధాంతము)
AB² = (x² – x₁)² + (y² – y₁)²
∴ AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
∴ A(x₁, y₁), B(x₂, y₂) బిందువుల మధ్య దూరం.
AB = d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Note:
(i) a) మూలబిందువు (0, 0) నుండి A (x₁, y₁) బిందువుకు గల దూరం \(\sqrt{x_{1}^{2}+y_{1}^{2}}\) అవుతుంది.
b) A (x₁, 0), B (0, y₁) లు X, Y – అక్షాలపై గల బిందువులు. A, B ల మధ్య దూరం = \(\sqrt{x_{1}^{2}+y_{1}^{2}}\)

(ii) A, B, C బిందువులు సరేఖీయాలైతే
AB + BC = AC లేదా AC + CB = AB లేదా AB + AC = BC అవుతుంది.

(iii) A, B, C లు త్రిభుజ శీర్షాలైతే .
AB = BC = AC అయితే ∆ABC సమబాహు త్రిభుజాన్ని, AB, BC, ACలలో ‘ఏ రెండు భుజాలు , సమానమైన సమద్విబాహు త్రిభుజాన్ని, AB² + BC² = AC² లేదా AB² + AC² = BC² లేదా AC² + CB² = AB² అయితే లంబకోణ త్రిభుజాన్ని ఏర్పరుస్తాయి.

(iv) A, B, C, D బిందువులు చతుర్భుజ శీర్షాలైతే
(a) ఎదురెదురు భుజాలు సమానాలు మరియు కర్ణాలు కూడా సమానాలు అయితే ABCD దీర్ఘ చతురస్రం అవుతుంది. AB = CD, BC = AD మరియు AC = BD.
(b) నాలుగు భుజాలు సమానము మరియు కర్ణాలు సమానం అయితే ABCD చతురస్రం అవుతుంది. AB = BC = CD = AD మరియు AC = BD
(c) ఎదురెదురు భుజాలు సమానమైన సమాంతర చతుర్భుజం అవుతుంది. AB = CD, BC = AD.
(d) ఎదురెదురు భుజాలు సమానమై, కర్ణాలు సమానం కాకపోతే అది దీర్ఘ చతురస్రం కానటువంటి సమాంతర చతుర్భుజం అవుతుంది. AB = CD, BC = AD మరియు AC ≠ BD.
(e) నాలుగు భుజాలు సమానం అయితే రాంబస్ అవుతుంది. AB = BC = CD = AD. f) నాలుగు భుజాలు సమానం అయి కర్ణాలు సమానం కాకపోతే అది చతురస్రం కానటువంటి రాంబస్ అవుతుంది. (ఇక్కడ AB అనగా భుజం AB పొడవు అని అర్థం)

→ విభజన సూత్రం :
(i) \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) రేఖపై A, B ల మధ్య P అనే బిందువు AB రేఖాఖండాన్ని P బిందువు అంతరంగా AP : PB నిష్పత్తిలో విభజిస్తుంది అంటారు.
AP = m₁, PB = m₂, గా తీసుకొంటే A, B లను Pm₁: m₂, నిష్పత్తిలో అంతరంగా విభజిస్తుంది అంటాము.

(ii) \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) రేఖపై A, B బిందువుల మధ్య కాకుండా P బిందువు ఉంటే AB రేఖాఖండాన్ని P బిందువు బాహ్యంగా
AP : BP నిష్పత్తిలో విభజిస్తుంది అంటారు.

(iii) A (x₁, y₁), B(x₂, y₂) బిందువులను అంతరంగా విభజించే. బిందువు P యొక్క నిరూపకాలను కనుగొందాము.

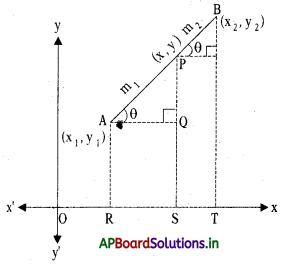
A(x₁, y₁), B(x₂, y₂) ఏవేని రెండు బిందువులు. P(x, y) అనేది AB ని అంతరంగా m₁ : m₂
నిష్పత్తిలో విభజిస్తుంది అనుకొందాం. \(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}\)
∆PAQ ~ ∆BPC (కో.కో.కో. నియమం) .
∴ \(\frac{\mathrm{PA}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{PC}}=\frac{\mathrm{PQ}}{\mathrm{BC}}\) ……..(1)
ప్రక్క పటం నుండి , AQ = RS = OS – OR = x – x₁
PC = ST = OT – OS = x₂ – x
PQ = PS – QS = y – y₁
BC = BT – CT =y₂ – y₁
పై విలువలు (1)లో రాయగా

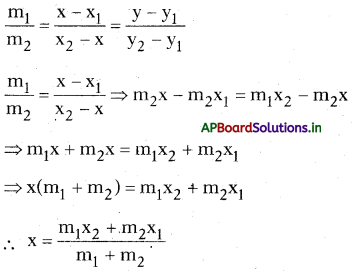
ఇదే విధంగా \(\frac{m_{1}}{m_{2}}=\frac{y-y_{1}}{y_{2}-y_{1}}\) తీసుకొంటే y = \(\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\) కాబట్టి A(x₁, y₁), B(x₂, y₂) లచే ఏర్పడే రేఖాఖండాన్ని m₁ : m₂డి నిష్పత్తిలో అంతరంగా విభజించే బిందువు
p(x, y) = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

Note:

• AB రేఖను P బిందువు k : 1 నిష్పత్తిలో అంతరంగా విభజిస్తున్నట్లయితే అప్పుడు P బిందువు నిరూపకాలు \(\left(\frac{\mathrm{kx}_{2}+\mathrm{x}_{1}}{\mathrm{k}+1}, \frac{\mathrm{ky}_{2}+\mathrm{y}_{1}}{\mathrm{k}+1}\right)\)
• \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) పై A, B బిందువులకు బాహ్యంగా P ఉంటే అప్పుడు m) ను -m,గా తీసుకొంటాము అలాంటి సందర్భంలో P నిరూపకాలు \(\left(\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}, \frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}\right)\)
• \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) పై A : B బిందువుకు P మధ్య బిందువు అయితే m, = m) అయి విభజన నిష్పత్తి 1 : 1 అవుతుంది. అప్పుడు P యొక్క నిరూపకాలు \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

→ త్రిభుజం యొక్క గురుత్వ కేంద్రము. : త్రిభుజం యొక్క మధ్యగత రేఖల మిళిత బిందువును ఆ త్రిభుజం యొక్క గురుత్వ కేంద్రము అంటాము. త్రిభుజ శీర్షం నుండి ఎదుటి భుజం మధ్య బిందువును కలిపే రేఖాఖండము మధ్యగతం అవుతుందని, మధ్యగతరేఖను గురుత్వ కేంద్రం 2 : 1 నిష్పత్తిలో విభజిస్తుందని మనకు తెలుసు. A(x¹, y¹), B(x², y²), C(x³, y³) లు ∆ABC యొక్క శీర్షాలు.. AD, BE, CF లు ∆ABC యొక్క మధ్యగతరేఖలు, 6 గురుత్వ కేంద్రం అనుకొందాం.

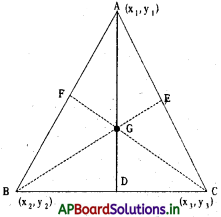
AD మధ్యగతరేఖ భూమి BC, మధ్య బిందువు AD గుండా పోతుంది.

∴ D = BC మధ్య బిందువు = \(\left(\frac{\mathrm{x}_{2}+\mathrm{x}_{3}}{2}, \frac{\mathrm{y}_{2}+\mathrm{y}_{3}}{2}\right)\)
AD మధ్యగతరేఖను గురుత్వ కేంద్రం G, 2 : 1 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
G(x, y) అనుకొంటే A(x₁, y₁), D = \(\left(\frac{\mathrm{x}_{2}+\mathrm{x}_{3}}{2}, \frac{\mathrm{y}_{2}+\mathrm{y}_{3}}{2}\right)\)

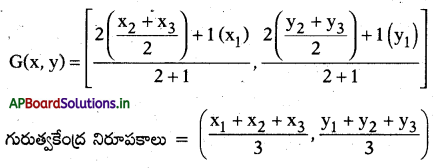
గురుత్వ కేంద్రాన్ని ‘కేంద్రాభాసం గరిమనాభి’ అని కూడా అంటారు.

→ ఒక రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు : ఒక రేఖాఖండమును మూడు సమాన భాగాలుగా విభజించు బిందువులను త్రిథాకరణ బిందువులు అంటారు.

AB రేఖాఖండం యొక్క ప్రాథాకరణ బిందువులు P, Q లు అయితే AP = PQ = QB అవుతుంది. . AB రేఖాఖండాన్ని P బిందువు AP : PB = 2 : 1 నిష్పత్తిలోను, Q బిందువు AQ : QB = 2 : 1 నిష్పత్తిలోను విభజిస్తుంది.

→ త్రిభుజ వైశాల్యము : ఏదేని త్రిభుజం ABC యొక్క శీర్షాలు A(x₁, y₁), B(x₂, y₂), C (x₃, y₃) అనుకొందాం.

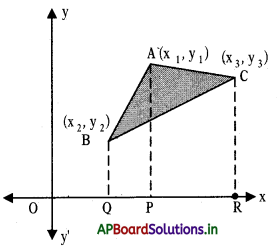
A, B మరియు C ల నుండి X – అక్షంపైకి AP, BQ మరియు CR అనే లంబరేఖలు గీయాలి. ఇప్పుడు.
BQ = y₂, PQ = OP – 0Q = x₁ – x₂
AP =y₁, PR = OR – OP = x₃ -x₁
CR = y₃, QR = OR – 0Q = x₃ – x₂
పటం నుండి ∆ABC వైశాల్యం = ట్రెపీజియం ABOP వైశాల్యం + ట్రెపీజియం APRC వైశాల్యం – ట్రెపీజియం BQRC వైశాల్యం. ట్రెపీజియం వైశాల్యం A = \(\frac{1}{2}\)(a + b) h లు సమాంతర భుజాలు, a, b లు సమాంతర భుజాలు, h వాని మధ్య దూరం.

∆ABC వైశాల్యం = \(\frac{1}{2}\)(BQ + AP) PQ + \(\frac{1}{2}\)(AP + CR) PR – \(\frac{1}{2}\)(BQ + CR) QR
= \(\frac{1}{2}\)(y₂ + y₁) (x₁ – x₂) + (y₁ + y₃) (x₃ – x₁) – (y₂ + y₃) (x₃ – x₂)
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂|

∴ (x₁, y₁), (x₂, y₂), (x₃, y₃) శీర్షాలుగా గల త్రిభుజ వైశాల్యము
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂|

గమనిక :
(i) A(x₁, y₁), B(x₂, y₂), C (x₃, y₃), D (x₄, y₄) లు చతుర్భుజ శీర్షాలైతే ఆ చతుర్భుజ వైశాల్యము :

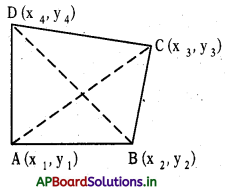
ABCD చతుర్భుజాన్ని కర్ణం సహాయంతో రెండు త్రిభుజాలుగా విభజించి త్రిభుజ వైశాల్య సూత్రాన్ని ఉపయోగించి చతుర్భుజ వైశాల్యాన్ని కనుగొంటాము.
రెండు త్రిభుజాలుగా విభజించుటకు ఏ కర్ణాన్నైనా (AC లేదా BD) తీసుకొనవచ్చును.

చతుర్భుజం ABCD వైశాల్యం = ∆ABC వైశాల్యం + ∆ACD వైశాల్యం
(లేదా)
= ∆ABD వైశాల్యం + ∆BDC వైశాల్యం

(ii) a) బిందువుల సరేఖీయత వైశాల్యము : A(x₁, y₁), B(x₂, y₂), C (x₃, y₃)లు సరేఖీయాలైతే ఆ మూడు బిందువుల ఒకే రేఖపై ఉండటం వలన త్రిభుజాన్ని ఏర్పరచలేవు. కావున ∆ABC వైశాల్యము సున్నా అవుతుంది. మూడు బిందువులతో ఏర్పడే త్రిభుజ వైశాల్యం సున్న అయితే ఆ మూడు బిందువులు సరేఖీయాలు అవుతాయి.
A, B, C లు సరేఖీయాలు ⇔∆ABC వైశాల్యము సున్న.
b) నాలుగు బిందువులు A, B, C, D లు సరేఖీయాలైతే చతుర్భుజం ABCD వైశాల్యము సున్నా అవుతుంది.

(iii) త్రిభుజ వైశాల్యము – హెరాన్ సూత్రం : a, b, c లు భుజాలుగాగల త్రిభుజ వైశాల్యం కనుగొనుటకు “హెరాన్” అనే గ్రీకు గణిత శాస్త్రవేత్త ఒక సూత్రాన్ని కనుగొన్నాడు. ఆ సూత్రం త్రిభుజ వైశాల్యం A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
ఇక్కడ S = \(\frac{a+b+c}{2}\)

సరళరేఖ వాలు : రెండు చరరాసులు x, y లలో ఏకఘాత సమీకరణం యొక్క సాధనలు ఒక సరళరేఖను ఏర్పరుస్తాయి. ఈ సరళరేఖ X – అక్షం యొక్క ధన దిశలో (అపసవ్య దిశ) చేసే కోణాన్ని ఆ సరళరేఖ యొక్క ఏటవాలు తనం అని, ఆ కోణం యొక్క Tan విలువను ఆ సరళరేఖ వాలు అని అంటారు.

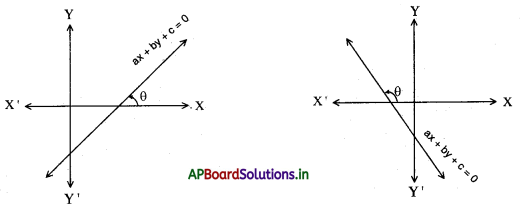
ax + by + c = 0 సరళరేఖ X – అక్షం అపసవ్య దిశలో చేసే కోణం θ అయిన ‘θ’ ను ax + by + c = 0 రేఖ యొక్క వాలుతనం అని, tan θ విలునను ax + by + c = 0 రేఖ వాలు అని అంటారు. .
ఒక రేఖపై నున్న బిందువుల నిరూపకాలలో Y నిరూపకాల భేదం మరియు X నిరూపకాల భేదంకు గల నిష్పత్తి వాలు (tan θ) కు సమానం అవుతుంది.

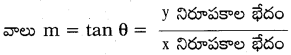
→ రెండు బిందువులను కలిపే రేఖవాలు : A(x₁, y₁), B(x₂, y₂) బిందువులను కలిపే రేఖ యొక్క వాలు m = tanθ = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

గమనిక :

• X – అక్షము మరియు X – అక్షానికి సమాంతరంగా గల రేఖ యొక్క వాలు సున్న.
  Y- అక్షము మరియు Y – అక్షానికి సమాంతరంగా గల రేఖ యొక్క వాలు నిర్వచింపబడదు.
• వాలు అధారంగా సరేఖీయత :
  A, B, C లు ఏవేని మూడు బిందువులై AB వాలు = BC వాలు = AC వాలు అయిన A, B, C బిందువులు సరేఖీయాలు అవుతాయి.

→ A, B, C బిందువులు సరేఖీయాలు అయితే

• A, B, C బిందువులతో ఏర్పడే ఏ రెండు రేఖాఖండాలైనా మూడవ రేఖాఖండానికి సమానం.
  AB + BC = AC లేదా AB + AC = BC లేదా AC + BC = AB
• A, B, C లతో ఏర్పడే త్రిభుజ వైశాల్యము సున్న.
• AB వాలు = BC వాలు = AC వాలు.