AP 10th Class Maths Notes 8th Lesson సరూప త్రిభుజాలు

Students can go through AP Board 10th Class Maths Notes 8th Lesson సరూప త్రిభుజాలు to understand and remember the concept easily.

AP Board 10th Class Maths Notes 8th Lesson సరూప త్రిభుజాలు

→ పైథాగరస్ (570-495 B.C.)

• పైథాగరస్ క్రీ.పూ. 570-495) ఒక గ్రీకు తత్త్వవేత్త మరియు గణిత శాస్త్రజ్ఞుడు.
• ఆయన గ్రీస్లోని సామోస్ ద్వీపంలో జన్మించారు. యువకుడిగా నా ఉన్నప్పుడు విజ్ఞాన సముపార్జన కోసం విస్తృతంగా పర్యటిస్తూ ఈజిప్టును మరియు ఇతర ప్రాంతాలను సందర్శించారు.
• ఆయన వేదాంతము, సంకేతము, గణితము, నీతి శాస్త్రము, రాజనీతి శాస్త్రములలో ఆసక్తిని కనబరచేవారు.
• ఆయన ఖగోళ శాస్త్రంలోను ముఖ్యమైన ఆవిష్కరణలు చేశారు. రి ఆయన గొప్ప గణిత శాస్త్రజ్ఞుడే కాదు గూఢ మతవాది, శాస్త్రవేత్త కూడా,
• క్రీ.పూ. 6వ శతాబ్దం చివరిలో తత్త్వశాస్త్రానికి, మతానికి ఎనలేని సేవలు చేశారు.
• ఆయన పేరు మీదనే పైథాగరస్ సిద్ధాంతం పేరుగాంచింది.
• పైథాగరస్ ఆలోచనలు, అభిప్రాయాలు తత్త్వవేత్త ప్లేటోపై, పాశ్చాత్య తత్త్వ శాస్త్రంపై గొప్ప ప్రభావం కనబరచాయి.

→ ఒకే ఆకారమును కలిగి ఉండి ఒకే పరిమాణము కలిగి ఉండనవసరములేని పటాలను సరూప పటాలు అంటారు.

→ వస్తువుల యొక్క ఎత్తులు మరియు దూరాలను సరూప పటాల నియమాలపై ఆధారపడి కనుగొంటారు.

→ జ్యామితిలో, భుజాల సంఖ్య సమానంగా ఉన్న రెండు బహుభుజులు సరూపాలు కావలెనన్న వాటి అనురూప కోణాలు సమానంగాను, అనురూప భుజాలు ఒకే నిష్పత్తిలో (లేదా) అనుపాతంలోనూ ఉండాలి.

→ ఒక బహుభుజిలో భుజాలన్నీ మరియు కోణాలన్నీ సమానంగా ఉంటే దానిని క్రమ బహుభుజి అంటారు. → అనురూప భుజాల నిష్పత్తిని సాధారణంగా స్కేలు (లేదా) స్కేలు గుణకం (లేదా) ప్రత్యామ్నాయ గుణకం అంటారు.

→ సమాన సంఖ్యలో భుజాలు కల్గిన రెండు బహుభుజులు సరూపాలు కావాలంటే

• వాటి అనురూప కోణాలు సమానంగా ఉండాలి.
• వాటి అనురూప భుజాలు ఒకే నిష్పత్తిలో ఉండాలి (అనుపాతంలో ఉండాలి). ఈ బహుభుజుల సరూపకతకు పై రెండు నియమాలలో ఏదో ఒక నియమము సరిపోదు. కాని త్రిభుజాలకు మాత్రం పై రెండింటిలో ఏదో ఒక నియమం సరిపోతుంది.

→ రెండు త్రిభుజాలు సరూపాలు కావాలంటే

1. వాటి అనురూప కోణాలు సమానంగా ఉండాలి.
2. వాటి అనురూప భుజాలు ఒకే నిష్పత్తిలో ఉండాలి.

→ ‘K’, స్కేలు గుణకము విలువ అయిన
K> 1 అయిన పెద్దవి చేయబడిన పటాలు
K= 1 అయిన సర్వసమాన పటాలు
K<1 అయిన చిన్నవి చేయబడిన పటాలు ఏర్పడతాయి.
ప్రాథమిక అనుపాత సిద్ధాంతము (థేల్స్ సిద్ధాంతము)

→ ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరు వేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి.

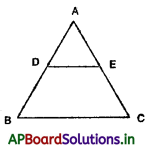
∆ABC లో; DE ∥ BC అయిన \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\). దీనినే ‘థేల్స్’ సిద్ధాంతము (లేక) ప్రాథమిక అనుపాత సిద్ధాంతము అంటారు.

→ ఒక త్రిభుజములో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు . .. సరళరేఖ, మూడవ భుజానికి సమాంతరంగా ఉండును.
∆ABCలో, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) అయిన l ∥ BC అగును.

దీనినే ‘థేల్స్ సిద్ధాంతపు విపర్యయము’ లేదా ‘ప్రాథమిక సిద్ధాంతపు విపర్యయము’ అంటారు. కో.కో.కో. నియమం :

→ రెండు త్రిభుజాలలో అనురూపక కోణాలు సమానంగా ఉంటే, వాటి అనురూప భుజాల నిష్పత్తులు సమానంగా ఉంటాయి (అనుపాతంలో వుంటాయి), ఇంకా ఆ రెండు త్రిభుజాలు సరూప త్రిభుజాలు అవుతాయి.

→ ∆ABC, ∆DEFలలో
∠A = ∠D, ∠B = ∠E, ∠C = ∠F అయిన
⇒ \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) అగును.

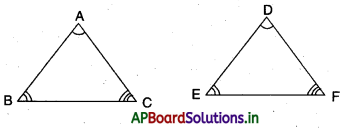
∴ ∆ABC ~ ∆DEF (కో.కో.కో. సరూపకత).

→ రెండు త్రిభుజాలలో, ఒక త్రిభుజములోని భుజాలు వేరొక త్రిభుజములోని భుజాలకు అనుపాతములో ఉన్న ఆ రెండు త్రిభుజాలలోని అనురూప కోణాలు సమానము మరియు ఆ రెండు త్రిభుజాలు సరూఫాలు.

→ ∆ABC, ∆DEF లలో,
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) కావున
∠A = ∠D, ∠B = ∠E, మరియు∠C = ∠F

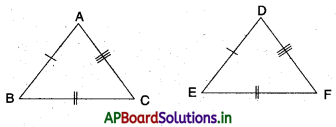
∴ ∆ABC ~ ∆DEF (కో.కో.కో సరూపకత). భు.భు. భు. సరూపత నియమం :

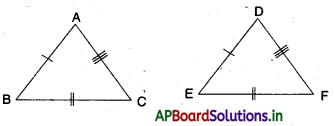
→ ఒక త్రిభుజములోని ఒక కోణము, వేరొక త్రిభుజములోని ఒక కోణమునకు సమానమై, ఈ కోణాలను కల్గి వున్న భుజాలు అనుపాతంలో ఉంటే ఆ రెండు త్రిభుజాలు సరూపాలు.

→ ∆ABC మరియు ∆DEF లలో \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) మరియు
∠A = ∠D అయిన

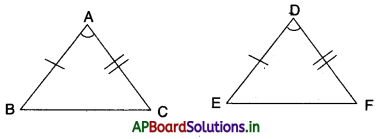
∆ABC ~ ∆DER (భు. కో. భు సరూపకత).

→ రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము.

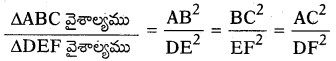
→ ఒక లంబకోణ త్రిభుజములో, లంబకోణము కల్గిన శీర్షము నుండి కర్ణానికి లంబము గీసిన, ఆ లంబానికి ఇరువైపులా ఏర్పడిన త్రిభుజాలు, ఇచ్చిన త్రిభుజానికి సరూపాలు మరియు అవి ఒకదానికొకటి కూడా సరూపాలు.

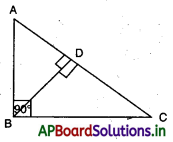
∆ABCలో, ∠B = 90°, BD ⊥ AC అయిన
∆ADB ~ ∆BDC ~ ∆ABC మరియు BD² = AD . DC

పైథాగరస్ సిద్ధాంతము :

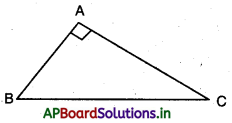
→ ఒక లంబకోణ త్రిభుజములో కర్ణము మీది వర్గము, మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానము.
∆ABCలో; ∠A = 90° అయిన AB² + AC² = BC²

పైథాగరస్ సిద్ధాంత విపర్యము : –
→ ఒక త్రిభుజములో ఒక భుజము మీది వర్గము మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానమైన, మొదటి భుజానికి ఎదురుగా ఉండే కోణము లంబకోణము అనగా త్రిభుజము లంబకోణ త్రిభుజమవుతుంది.

→ ఒక వాక్యము సత్యముగాని, అసత్యముగాని ఏదో ఒకటి మాత్రమే అగునటువంటి వాక్యమును “ప్రవచనము” అంటారు.

→ ఒక ప్రవచనముకు చివరన “కాదు” చేర్చడం వలన ఏర్పడు కొత్త ప్రవచనమును వ్యతిరేక ప్రవచనము అంటారు.

→ ‘p’ అను ప్రవచనము యొక్క వ్యతిరేక ప్రవచనమును “~p” తో సూచిస్తారు.

→ రెండు సరళ ప్రవచనాలను కలుపగా ఏర్పడు నూతన ప్రవచనమును సంయుక్త ప్రవచనం అంటారు.

→ రెండు సరళ ప్రవచనాలను “అయినచో” చే కలుపగా ఏర్పడిన సంయుక్త ప్రవచనాన్ని “అనుషంగికము” లేదా “నియత ప్రవచనము” అంటారు.

→ రెండు సరళ ప్రవచనాలను p మరియు q లను “అయినచో” కలుపగా “p అయినచో q” అని వస్తుంది. దీనిని మనం p ⇒ q అని రాస్తాము.

→ p ⇒ q లో మనము p, q లను తారుమారు చేయగా q ⇒ p ఏర్పడును. దీనినే మనం ప్రవచన విపర్యయము అంటాము.
ఉదా : ∆ABC లో AB = AC అయితే C = ∠B, ఈ ప్రవచనపు విపర్యయము ∆ABC లో C = ∠B అయితే AB = AC అగును.