Students can go through AP Board 6th Class Maths Notes 4th Lesson పూర్ణసంఖ్యలు to understand and remember the concept easily.
AP Board 6th Class Maths Notes 4th Lesson పూర్ణసంఖ్యలు
→ బ్రహ్మగుప్త (598-670 AD):
మొట్టమొదటిసారిగా రుణ సంఖ్యలను సూచించడానికి ప్రత్యేక గుర్తు (-) వాడినట్లు తెలుస్తున్నది. ధనాత్మక మరియు రుణాత్మక పరిమాణాలను తెలుసుకోవడానికి కొన్ని సూత్రాలు ప్రతిపాదించాడు.
పూర్ణ సంఖ్యలను సూచించుటకు “Z” అనే అక్షరాని జర్మను మొదటిసారిగా వాడారు. “Z” అంటే జర్మన్ భాషలో ‘జెలెస్’ “Zehlen” అంటే “సంఖ్య” అని అర్థం.
→ సున్న కన్నా చిన్న సంఖ్యలను రుణసంఖ్యలు అంటారు. సున్న కన్నా పెద్ద సంఖ్యలను ధన సంఖ్యలు అంటారు. సున్న (0) అనేది ధన సంఖ్య కాదు మరియు రుణ సంఖ్య కాదు.
→ ధన పూర్ణసంఖ్యలు, సున్న మరియు రుణ పూర్ణ సంఖ్యలు కలిసి పూర్ణసంఖ్యలు ఏర్పడతాయి. పూర్ణ సంఖ్యల సంఖ్యాసమితిని “Z” లేదా “I” అనే అక్షరాలతో సూచిస్తారు.
Z = {……….. – 4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ……….}
ఏదైనా సంఖ్యకు గుర్తు ఇవ్వనిచో దానిని ధనసంఖ్యగా పరిగణిస్తాము.
![]()
→ సంఖ్యారేఖ పై రుణపూర్ణ సంఖ్యలను సున్న (0) కు ఎడమవైపున, ధనపూర్ణ సంఖ్యలను సున్న (0) కు కుడివైపున సూచిస్తూ సంఖ్యారేఖను గీస్తాము.
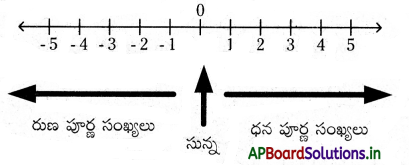
→ పూర్ణ సంఖ్యల సంఖ్యారేఖను నిలువుగా కూడా గీయవచ్చును. నిలువుగా గీచిన సంఖ్యారేఖపై సున్న (0)కు పై భాగంలో ధన పూర్ణ సంఖ్యలను, సున్న (0) కు కింది భాగాన రుణ పూర్ణసంఖ్యలను సూచిస్తాము.
→ సహజసంఖ్యలు N = {1,2,3,4, ….} లను ధనపూర్ణసంఖ్యలు (Z+) అని, పూర్ణాంకాలను W = {0, 1, 2, 3, 4, …} లను రుణేతరపూర్ణసంఖ్యలు అనీ, {…….. – 4, -3, -2, -1} లను రుణపూర్ణసంఖ్యలు (Z–) అని అంటాము.
→ సున్న (0) ధనపూర్ణ సంఖ్య కాదు, రుణ పూర్ణ సంఖ్య కాదు. రుణ పూర్ణసంఖ్యలు ఆ ధన పూర్ణసంఖ్యలు

→ సంఖ్యారేఖ పై కుడివైపునకు పోయే కొలదీ సంఖ్య విలువ పెరుగుతుంది. అలాగే ఎడమవైపుకు పోయే కొలదీ తగ్గుతుంది. అనగా సంఖ్యారేఖ పై ఒక సంఖ్యకు కుడివైపుగల సంఖ్య ఆ సంఖ్య కన్నా పెద్దది. అలాగే ఎడమవైపుగల సంఖ్య ఆ సంఖ్య కన్నా చిన్నది.

-2నకు -1 కుడివైపున కలదు కావున -1 > -2 –
అలాగే – 2 నకు – 4 ఎడమవైపు కలదు కావున 4 < -2
సంఖ్యారేఖపై సంకలనం చేయుటకు ధనసంఖ్యను కూడవలసిన సందర్భంలో కుడివైపునకు, రుణసంఖ్యను కూడవలసిన సందర్భంలో ఎడమవైపునకు కదలాలి.
ఉదా : (i) 3 + (-1)
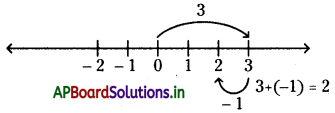
(ii) (-3) + (-2)
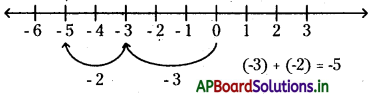
→ ఏవేని రెండు సంఖ్యల మొత్తం సున్న (0) అయితే ఆ సంఖ్యలను ఒకదానికొకటి సంకలన విలోమం అంటారు.
ఉదా : (3) + (-3) = 0 కావున 3 యొక్క సంకలన విలోమం = -3
-3 యొక్క సంకలన విలోమం = 3
→ a ఏదేని పూర్ణ సంఖ్య అయిన a యొక్క సంకలన విలోమం =-a
అలాగే -a యొక్క సంకలన విలోమం = a
∴ -(-a) = a .
→ రెండు ధనపూర్ణసంఖ్యల మొత్తం ఎల్లప్పుడు ధనపూర్ణసంఖ్య మరియు రెండు రుణపూర్ణసంఖ్యల మొత్తం ఎల్లప్పుడు రుణ పూర్ణసంఖ్య.
![]()
→ ఒక ధనపూర్ణసంఖ్య, మరొక రుణపూర్ణసంఖ్యల మొత్తం ఒక ధనపూర్ణసంఖ్య లేదా ఒక రుణపూర్ణసంఖ్య లేదా సున్న కావచ్చును.
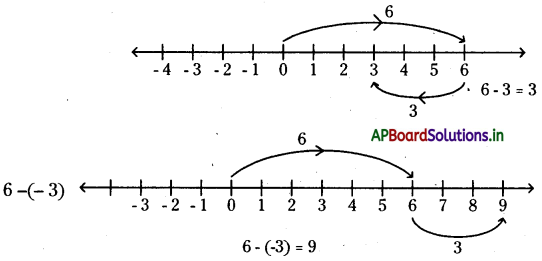
→ ఒక సంఖ్యను సంఖ్యారేఖ పై మరొక సంఖ్య నుండి తీసివేయు (వ్యవకలనం) సందర్భంలో ధన సంఖ్యను తీసివేయు సందర్భంలో ఎడమవైపునకు, రుణసంఖ్యను తీసివేయు సందర్భంలో కుడివైపునకు కదలాలి.
ఉదా : 6 – 3