Students can go through AP Board 6th Class Maths Notes 5th Lesson భిన్నాలు – దశాంశ భిన్నాలు to understand and remember the concept easily.
AP Board 6th Class Maths Notes 5th Lesson భిన్నాలు – దశాంశ భిన్నాలు
→ భిన్నం అనగా ఒక వస్తువు లేదా వస్తు సముదాయంలో కొంతభాగం.
ఉదాహరణ : భిన్నం \(\frac{3}{5}\) అనేది 5 భాగాలలో 3 భాగాలు అని తెలియజేస్తుంది.
\(\frac{3}{5}\) లో 3ను లవం అని, 5ను హారం అని అంటారు.
→ భిన్నాలు – రకాలు :
(i) క్రమ భిన్నం : భిన్నంలో లవం, హారం కన్నా తక్కువ అయితే ఆ భిన్నాన్ని క్రమభిన్నం అంటారు.
ఉదాహరణ : \(\frac{3}{4}, \frac{5}{8}, \frac{14}{19}\)……………
క్రమభిన్నం విలువ ఎల్లప్పుడు 1 కన్నా తక్కువ.
(ii) అపక్రమ భిన్నం : భిన్నంలో హారం కన్నా లవం ఎక్కువ లేదా సమానంగా గల భిన్నాన్ని అపక్రమభిన్నం అంటారు.
ఉదాహరణ : \(\frac{7}{3}, \frac{11}{5}, \frac{5}{5}\)
అపక్రమ భిన్నం విలువ ఎల్లప్పుడు 1 లేదా 1 కన్నా ఎక్కువగా ఉంటుంది.
(iii) మిశ్రమ భిన్నం : పూర్ణాంకం మరియు క్రమభిన్నాలు సమూహంగా గల భిన్నాన్ని మిశ్రమ భిన్నం అంటారు.
ఉదాహరణ : \(\frac{11}{5}, \frac{4}{3}, \frac{15}{7}\)
→ సమాన భిన్నాలు : ఒకే విలువను కలిగి వేర్వేరు రూపాలలో గల భిన్నాలను సమాన భిన్నాలు అంటారు.
ఉదాహరణ : \(\frac{1}{2}=\frac{2}{4}=\frac{3}{6}\) = ………….
ఒక భిన్నం యొక్క లవ, హారాలను ఒకే సంఖ్యతో గుణించడం లేదా భాగించడం ద్వారా సజాతి భిన్నాలు రాయవచ్చును.
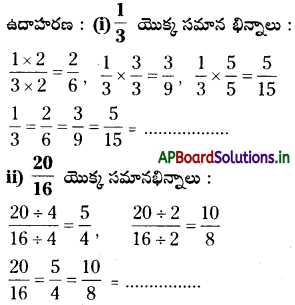
→→ సజాతి భిన్నాలు : ఒకే హారం కల్గియున్న భిన్నాలను “సజాతి భిన్నాలు” అంటారు.
ఉదాహరణ : \(\frac{5}{12}, \frac{7}{12}, \frac{18}{12}\)………………..
→ విజాతి భిన్నాలు : వివిధ (వేర్వేరు) రకాల హారాలతో కూడియున్న భిన్నాలను “విజాతి భిన్నాలు” అంటారు.
ఉదాహరణ : \(\frac{1}{2}, \frac{3}{4}, \frac{5}{7}, \frac{6}{11}\) ………….
→ భిన్నాల కనిష్ఠదూరం : భిన్నంలో లవం మరియు హారాలకు 1 తప్ప ఉమ్మడి కారణాంకం (లవ, హారాల గ.సా.భా 1) లేనట్లయిన ఆ భిన్నం కనిష్ఠ రూపంలో ఉంది అంటాము.
ఉదాహరణ : \(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}, \frac{4}{8}\)……… యొక్క కనిష్టరూపం = ;
![]()
→ భిన్నాల పోలిక :
(i) రెండు భిన్నాలు ఒకే హారం కలిగి ఉంటే, వాటిలో లవం తక్కువ గల భిన్నం వాటిలో చిన్న భిన్నం అవుతుంది.
ఉదాహరణ : \(\frac{2}{7}\) మరియు \(\frac{5}{7}\) లలో \(\frac{2}{7}, \frac{5}{7}\) కన్నా చిన్నది.
\(\frac{2}{7}<\frac{5}{7}\)
(ii) రెండు భిన్నాలు ఒకే లవం కలిగి ఉంటే, వాటిలో హారం తక్కువగాగల భిన్నం పెద్ద భిన్నం అవుతుంది.
\(\frac{2}{7}\) మరియు \(\frac{2}{11}\)లలో \(\frac{2}{7}, \frac{2}{11}\) కన్నా పెద్దది.
\(\frac{2}{7}<\frac{2}{11}\)
(iii)విజాతి భిన్నాలను క.సా.గు ద్వారా సజాతి భిన్నాలుగా మార్చి పోల్చుతాం.
\(\frac{2}{5}\) మరియు \(\frac{3}{4}\) లను పోల్చుదాం.
5, 4 ల క.సా.గు.
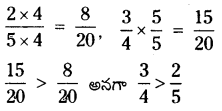
→ భిన్నాల సంకలనం మరియు వ్యవకలనం :
(i) సజాతి భిన్నాల సంకలనం, వ్యవకలనం :
సజాతి భిన్నాలను కూడిక లేదా తీసివేసేటప్పుడు లవాలను మాత్రమే కలపడం లేదా తీసివేయడం ద్వారా వచ్చిన ఫలితాన్ని లవంగాను, సామాన్య హారాన్ని హారంగాను రాస్తాము.
ఉదా : \(\frac{3}{7}+\frac{2}{7}=\frac{3+2}{7}=\frac{5}{7}, \frac{3}{7}-\frac{2}{7}=\frac{3-2}{7}=\frac{1}{7}\)
(ii) విజాతి భిన్నాల సంకలనం, వ్యవకలనం :
విజాతి భిన్నాల కూడిక లేదా తీసివేత చేయుట.
అ) హారాల క.సా.గు. కనుగొనడము.
ఆ) భిన్నాలలో హారాన్ని, సమానం చేసి సజాతి భిన్నాలుగా మార్చడము.
ఇ) సజాతి భిన్నాలను కూడిక లేదా తీసివేత చేయడం.

→ భిన్నాల గుణకారం :
(i) భిన్నాన్ని ఒక పూర్ణాంకంతో గుణించటం :
భిన్నాన్ని పూర్ణాంకంతో గుణించునపుడు మొదట పూర్ణాంకంచే భిన్నంలో లవాన్ని గుణించి, భిన్నంలో హారాన్ని అదేవిధంగా రాయాలి.
ఉదాహరణ : 2 × \(\frac{3}{5}=\frac{2 \times 3}{5}=\frac{6}{5}\)
(ii) మిశ్రమ భిన్నాన్ని పూర్ణాంకంచే గుణకారం చేయాలంటే ముందుగా మిశ్రమ భిన్నాన్ని, అపక్రమ భిన్నంగా మార్చి పై విధంగా గుణించాలి.
2 × \(3 \frac{5}{7}=2 \times \frac{26}{7}=\frac{2 \times 26}{7}=\frac{52}{7}\)
→ భిన్నాన్ని, భిన్నంతో గుణించడము :
భిన్నాన్ని, భిన్నంతో గుణకారం చేయాలంటే రెండు భిన్నాలలోని లవాలను గుణించి లబ్దాన్ని లవంగాను, హారాన్ని హారంతో గుణించి లబ్దాన్ని హారంగాను రాయాలి.
ఉదాహరణ : \(\frac{3}{5} \times \frac{4}{7}=\frac{3 \times 4}{5 \times 7}=\frac{12}{35}\)
![]()
→ భిన్నాల భాగహారము :
(i) పూర్ణాంకాన్ని భిన్నంచే భాగించుట :
పూర్ణాంకాన్ని భిన్నంచే భాగించాలంటే పూర్ణాంకాన్ని భాగించాల్సిన భిన్నం యొక్క వ్యుత్రమం (గుణకార విలోమం)చే
3 ÷ \(\frac{2}{5}=3 \times \frac{5}{2}=\frac{15}{2}\) (\(\frac{2}{5}\) యు వ్యుత్తమం \(\frac{5}{2}\))
(ii) భిన్నాన్ని పూర్ణాంకంచే భాగించుట : భిన్నాన్ని పూర్ణాంకంచే భాగించాలంటే, ఆ భిన్నాన్ని భాగించాల్సిన పూర్ణాంకం యొక్క వ్యుత్ర మంచే గుణించాలి.
\(\frac{2}{3} \div 5=\frac{2}{3} \times \frac{1}{5}=\frac{2}{15}\) (5 యొక్క వ్యుత్రమం \(\frac{1}{5}\))
గమనిక : పూర్ణాంకాన్ని మిశ్రమ భిన్నంచే గుణించాల్సి వచ్చినా లేదా మిశ్రమభిన్నాన్ని పూర్ణాంకంతో భాగించాల్సి వచ్చినా మొదట మిశ్రమ భిన్నాన్ని, అపక్రమభిన్నంగా మార్చి పై తెల్పినవిధంగా భాగహారం చేయాలి.
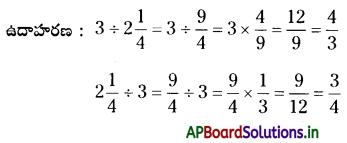
(iii) భిన్నాన్ని మరొక భిన్నంతో భాగించడము :
ఒక భిన్నాన్ని, మరొక భిన్నంతో భాగించాల్సి వచ్చినపుడు మొదటి భిన్నాన్ని (భాగింపబడుతున్న), రెండవ భిన్నం (భాగిస్తున్న) యొక్క వ్యుత్ర మంచే గుణించాలి.
ఉదాహరణ : \(\frac{2}{3} \div \frac{5}{7}=\frac{2}{3} \times \frac{7}{5}=\frac{14}{15}\)
\(\frac{5}{7}\) యొక్క వ్యతమం \(\frac{7}{5}\)
→ దశాంశ సంఖ్యలు :
భిన్నం యొక్క మరొక రూపమే దశాంశము. హారం 10, 100, 1000, 10000, ……. గా గల భిన్నాలను దశాంశ భిన్నాలని అంటారు.
ఉదాహరణ :
\(\frac{1}{10}, \frac{3}{10}, \frac{4}{100}, \frac{345}{100}, \frac{674}{10000}\)
- \(\frac{1}{10}\)ని 0.1 గా రాస్తాము. 0.1 ని దశాంశం అని అంటారు.
- \(\frac{1}{100}\) = 0.01 గా రాస్తాము. 0.01 ని శతాంశం అని అంటాము. 100
- \(\frac{1}{1000}\) = 0.001 గా రాస్తాము. 0.001 ని సహస్రాంశం అని అంటారు. 1000
\(\frac{45}{10}=4 \frac{5}{10}\) = 4.5
\(\frac{473}{100}=4 \frac{73}{100}\) = 4.73లో
4ను పూర్ణాంకభాగం అని, 73ను దశాంశ భాగం అని, ‘.’ ను దశాంశ బిందువు అని అంటారు.
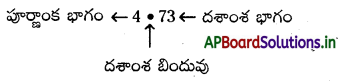
పూర్ణాంకభాగం ఎల్లప్పుడు 0 లేదా అంతకన్నా ఎక్కువ ఉంటుంది. దశాంశ భాగం ఎల్లప్పుడు 1 కన్నా తక్కువ.
→ దశాంశ భిన్నాల స్థానవిలువలు – విస్తరణ రూపం :

= 4 × 1000 + 3 × 100 + 7 × 10 + 2 × 1 + 4 × \(\frac{1}{10}\) + 6 × \(\frac{1}{100}\) + 5 × \(\frac{1}{1000}\)
= 4 వేలు + 3 వందలు + 7 పదులు + 2 ఒకట్లు + 4 దశాంశాలు + 6 శతాంశాలు + 5 సహస్రాంశాలు
→ భిన్నాలను దశాంశరూపంలోనికి, దశాంశరూపం నుండి భిన్నరూపంలోకి మార్చడము :
(i) హారం 10, 100, 1000, …… గా గల భిన్నాలను సులభంగా దశాంశరూపంలోనికి మార్చవచ్చును. ..

హారంలో 10 ఉన్నప్పుడు దశాంశస్థానాల సంఖ్య 1. 100 ఉన్నప్పుడు దశాంశ స్థానాల సంఖ్య 2. 1000 ఉన్నప్పుడు దశాంశ స్థానాల సంఖ్య 3 వస్తాయి.
(ii) సామాన్య భిన్నాలను 10, 100, 1000, ……… హారాలుగా గల సమాన భిన్నాలుగా మార్చి పై విధంగా దశాంశ రూపాన్ని రాస్తాము.
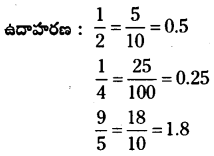
→ సమాన దశాంశ భిన్నాలు :

∴0.4 = 0.40 = 0.400 అవుతాయి.
→ సజాతి, విజాతి దశాంశ భిన్నాలు :
(i) సజాతి దశాంశ భిన్నాలు : సమానసంఖ్యలో దశాంశ స్థానాలను కలిగిన దశాంశ భిన్నాలను సజాతి దశాంశ భిన్నాలు అంటారు.
ఉదాహరణ : 0.7, 1.3, 7.4, 12.6 ఒక దశాంశస్థానం కలిగినవి.
0.34, 6.73, 9.46, 13.98 రెండు దశాంశ స్థానాలు కలిగినవి.
(ii) విజాతి దశాంశ భిన్నాలు : వేర్వేరు సంఖ్యలో దశాంశస్థానాలను కలిగిన దశాంశ భిన్నాలను విజాతి దశాంశ భిన్నాలు అంటారు.
ఉదాహరణ : 0.7, 6.73, 4.762, …… .
→ దశాంశ భిన్నాల పోలిక, క్రమం :
దశాంశ భిన్నాలను పోల్చడానికి మనం కింది సోపానాలు అనుసరించాలి.
- సోపానం 1: ఇచ్చిన దశాంశాలను సజాతి దశాంశాలుగా మార్చుకోవాలి.
- సోపానం 2 : ముందు పూర్ణాంక భాగాలను పోల్చి, పూర్ణాంక భాగంలో ఏది పెద్దదైతే అది పెద్దది.
- సోపానం 3 : పూర్ణాంక భాగాలు సమానం అయితే దశాంశ భాగంను పోల్చి, దశాంశ భాగంలో ఏది పెద్దదైతే అది పెద్దది. అంది.
- సోపానం 4 : పూర్ణాంక భాగం మరియు దశాంశభాగం రెండూ సమానమైతే పై విధానాన్ని శతాంశానికి అమలు పరచాలి.
ఉదాహరణ: 3.637 మరియు 3.654 లలో
3.654 > 3.637 (పూర్ణాంకభాగం, దశాంశ భాగం సమానం కావున శతాంశభాగం ఆధారంగా పోల్చాము)
→ దశాంశ భిన్నాల సంకలనం, వ్యవకలనమును ఇచ్చిన దశాంశ భిన్నాలను సజాతి దశాంశ భిన్నాలుగా మార్చి పూర్ణాంకాల సంకలనం, వ్యవకలనం వలే చేయాలి.
ఉదా : 3.4 + 7.63 + 34.379 :
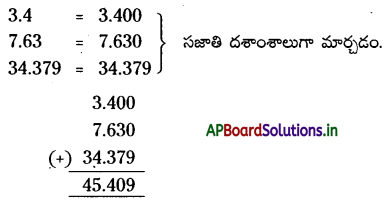
![]()
→ దశాంశ భిన్నాలను మనం ద్రవ్యం, దూరం, పొడవు, బరువు మరియు పరిమాణాలతో ఉపయోగిస్తాము.
- 100 పైసలు = ₹ 1 కావున 1 పైసా = ₹ \(\frac{1}{100}\) = ₹ 0.01
- 100 సెం.మీ. = 1 మీ. కావున 1 సెం.మీ. \(\frac{1}{100}\) మీ. = 0.01 మీ.
- 1000 మీ. = 1 కి.మీ. కావున 1 మీ. = \(\frac{1}{1000}\) కి.మీ. = 0.001 కి.మీ.
- 1000 గ్రా. = 1 కి.గ్రా. కావున 1 గ్రా. .= \(\frac{1}{1000}\) కి.గ్రా. = 0.001 కి.గ్రా.
- 1000 మి.లీ. = 1 లీ. కావున 1 మి.లీ. = \(\frac{1}{1000}\) లీ. = 0.001 లీ.