Students can go through AP Board 6th Class Maths Notes 8th Lesson జ్యామితీయ భావనలు to understand and remember the concept easily.
AP Board 6th Class Maths Notes 8th Lesson జ్యామితీయ భావనలు
→ బిందువు : పొడవు, వెడల్పులు లేని జ్యామితీయ ఆకారం బిందువు. బిందువులను సూచించుటకు మనం సాధారణంగా ఆంగ్ల పెద్ద అక్షరాలు A, B, C, …. లతో సూచిస్తాము.
→ స్కేలు, విభాగిని, వృత్తలేఖిని సహాయంతో మనం రేఖాఖండం పొడవును కొలుస్తాము.
→ రేఖ : రెండు వైపులా అనంతంగా విస్తరించిన రెండు కిరణాల సమ్మేళనం. దీనిని \(\overrightarrow{\mathrm{AB}}\) లేదా l, m అనే చిన్న అక్షరాలతో సూచిస్తారు.
→ ఖండన రేఖలు : సమతలంలోనే రెండు రేఖలకు ఒకే ఉమ్మడి బిందువు ఉంటే వాటిని ఖండన రేఖలు అంటారు. ఉదాహరణ : ‘m’ రేఖపై A, B, C బిందువులు, ‘l’ రేఖపై D, A,E బిందువులు కలవు. A బిందువు రెండు రేఖలపై కలదు. అనగా A ఉమ్మడిబిందువు. l, m లు ఖండనరేఖలు అవుతాయి.
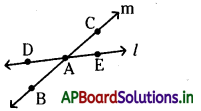
→ సమాంతర రేఖలు : సమతలంలో రెండు రేఖలకు ఉమ్మడి బిందువు లేకుంటే వాటిని సమాంతర రేఖలు అంటారు.
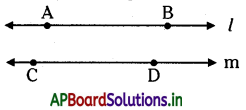
l, m రేఖలకు ఉమ్మడిబిందువులు లేవు. l m లు సమాంతర రేఖలు.
సమాంతరరేఖలను ∥ గుర్తుతో సూచిస్తాము.
పై l, m రేఖలను l ∥ m లేదా \(\overrightarrow{\mathrm{AB}} / / \overrightarrow{\mathrm{CD}}\) గా సూచిస్తాము.
![]()
→ మిళిత రేఖలు : రెండు కన్నా ఎక్కువ రేఖలకు ఒకే ఉమ్మడి బిందువు ఉంటే, ఆ రేఖలను మిళిత రేఖలు అంటారు. ఆ ఉమ్మడి బిందువును మిళిత బిందువు అంటారు.
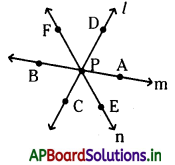
పై పటంలో l, m, n రేఖల ఉమ్మడి బిందువు P. (అనగా l, m, n రేఖలు ఒకదానికొకటి P వద్ద ఖండించుకొంటున్నాయి)
→ లంబరేఖలు : ఖండనరేఖలలో ఒక ప్రత్యేక సందర్భమే లంబరేఖలు. ఈ లంబరేఖలకు పుస్తకం పక్కపక్క అంచులు, నల్లబల్ల పక్క పక్క అంచులు, తలుపు పక్కపక్క అంచులను ఉదాహరణలుగా మనం చెప్పవచ్చును. లంబరేఖలను ‘⊥’ గుర్తుతో సూచిస్తాము.
→ రెండు లంబరేఖల మధ్యకోణము 90°.
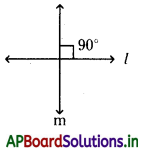
పై పటంలోని l, m రేఖలు లంబరేఖలు. వీనిని l ⊥ m గా రాస్తాము.
→ కోణాలు, అందులో రకాలు : కోణము : ఒకే తొలిబిందువును కలిగిన రెండు విభిన్న కిరణాల సమ్మేళనాన్ని కోణం అంటారు. ఉమ్మడి తొలి బిందువును శీర్షం అని, కోణం ఏర్పరిచిన కిరణాలను కోణ భుజాలు అని అంటారు. ప్రక్క పటంలో ‘O’ కోణశీర్షము.

\(\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}}\) లు కోణ భుజాలు. శీర్షమును ఆధారంగా చేసుకొని ఒక భుజం నుండి మరొక భుజం చేసే భ్రమణ (తిరిగిన) పరిమాణాన్ని కొలవడమే కోణాన్ని కొలవడము.
కోణాన్ని సూచించడానికి వివిధ పద్ధతులు కలవు.
- శీర్షం ఆధారంగా పై పటంలో కోణం ∠O,
- కోణశీర్షం, భుజాలపై గల బిందువుల ఆధారంగా ∠AOB లేదా ∠BOA.
- సంఖ్య ఆధారంగా ∠1 గా సూచిస్తాము.
→ కోణాన్ని కొలవడం – షష్ట్యంశమానం :
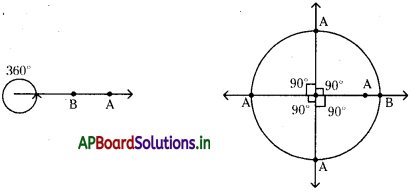
కోణాలను మనం కోణమానిని అనే పరికరాన్ని ఉపయోగించి కొలుస్తాము. మూల మట్టాలను ఉపయోగించి కొన్ని ప్రత్యేక కోణాలను కొలవవచ్చును (15°, 30°, 45°, 60°, 75°, 90°,….). శీర్షం ఆధారంగా కోణం యొక్క ఒక భుజం, మరొక భుజంతో ఒక పూర్తి భ్రమణం పూర్తి చేసిన అది చేసే కోణము 360° గా పరిగణిస్తాము. ఈ పూర్తిభ్రమణాన్ని 360 సమభాగాలు చేయగా అందులో ఒక భాగాన్ని 1° అంటారు.
→ లంబకోణము : పూర్తి భ్రమణాన్ని 4 సమభాగాలు చేయగా ప్రతి భాగం యొక్క కోణము ఒక లంబ కోణము అవుతుంది. లంబకోణం విలువ = \(\frac{360^{\circ}}{4}\) = 90°
→ అల్పకోణము : 90° కన్నా తక్కువగా గల కోణాన్ని అల్పకోణము అంటారు.
→ అధికకోణము : 90° కన్నా ఎక్కువ, 180° కన్నా తక్కువ గల కోణాన్ని అధిక కోణం అంటారు.
![]()
→ అధికతర లేదా పరావర్తన కోణము : 180° కన్నా ఎక్కువ, 360° కన్నా తక్కువ గల కోణాన్ని అధికతర లేదా పరావర్తన కోణం అంటారు.
→ సరళకోణం : 180° గల కోణాన్ని సరళకోణం అంటారు.
→ సంపూర్ణ లేదా పరిపూర్ణ కోణం : 360° కోణాన్ని సంపూర్ణ లేదా పరిపూర్ణ కోణం అంటారు.