Students can go through AP Board 7th Class Maths Notes 12th Lesson సౌష్ఠవము to understand and remember the concept easily.
AP Board 7th Class Maths Notes 12th Lesson సౌష్ఠవము
→ ఇచ్చిన పటాన్ని రెండు ఏకీభవించు భాగాలుగా ఒక రేఖ విభజించగలిగిన అప్పుడు ఆ పటం సౌష్ఠవంగా ఉంది అంటాము. విభజించే ఆ రేఖను ‘సౌష్ఠవ అక్షం’ లేదా ‘రేఖా సౌష్ఠం’ అంటారు.
→ ఒక పటం ఒకటి లేక అంతకన్నా ఎక్కువ సౌష్ఠవాక్షములు కలిగి ఉండవచ్చు.
→ ఒక పటంను దాని మధ్య బిందువుగుండా పటాన్ని కొంత కోణంతో భ్రమణం చేయగా ఏర్పడు పటం, మొదటి పటం వలే అదేవిధంగా ఉన్నచో ఆ పటం భ్రమణ సౌష్ఠం కలిగియున్నది అంటాం.
→ భ్రమణం చెందడంలో ఏర్పడే కోణాన్ని ‘భ్రమణ కోణం’ అంటారు.
→ అన్ని పటాలు 360° భ్రమణం చేసినపుడు దాని మొదటి స్థానంలో ఉన్న పటాలను చేరుకొనును. అది ‘1’ వ పరిమాణంగా – గల భ్రమణ సౌష్ఠవము కలిగి ఉంటుంది. అందువలన భ్రమణ సౌష్ఠవ పరిమాణం ‘1’ కంటే ఎక్కువ ఉన్న పటాలను మాత్రమే భ్రమణ సౌష్ఠవం కలిగియున్నాయి అంటాం.
![]()
→ కొన్ని ఆకారాలు రేఖా సౌష్ఠవాన్ని మాత్రమే కలిగి ఉంటాయి, కొన్ని ఆకారాలు భ్రమణ సౌష్ఠవాన్ని మాత్రమే కలిగి, ఉంటాయి మరికొన్ని ఆకారాలు రెండు రకాల సౌష్ఠవాలను కలిగి ఉంటాయి. చతురస్రాలు, సమబాహు త్రిభుజాలు మరియు వృత్తాలు, రేఖీయ మరియు భ్రమణసౌష్ఠవాలు రెండిటినీ కలిగి ఉంటాయి.
→ ప్రతి క్రమ బహుభుజిలో భుజాలు ఎన్ని ఉన్నాయో అన్ని రేఖా సౌష్ఠవాక్షాలను కలిగి ఉంటాయి.

→ సౌష్ఠవ అక్షం : పటాన్ని రెండు ఏకీభవించు భాగాలుగా ఒక రేఖ విభజించగలిగినపుడు ఆ పటం సౌష్ఠవంగా ఉంది అంటాము. అలా విభజించే రేఖను ‘సౌష్ఠవ అక్షం’ లేదా ‘రేఖా సౌష్ఠవం’ అంటారు.
→ ఒక పటం ఒకటి లేదా అంతకన్నా ఎక్కువ సౌష్ఠవాక్షాలను కలిగి ఉండవచ్చును.
ఉదా:
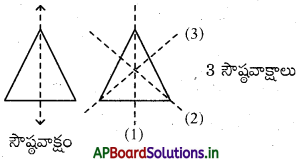
→ సమాన భుజాలు మరియు సమాన కోణాలు కలిగిన బహుభుజిని ‘క్రమ బహుభుజి’ అంటారు.
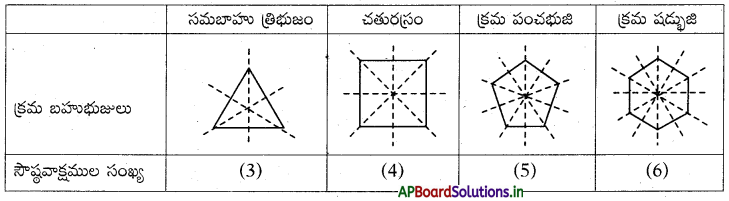
క్రమబహుభుజులకు వాని భుజాల సంఖ్యకు సమాన సంఖ్యలో సౌష్ఠవ అక్షాలు ఉంటాయి.
![]()
→ భ్రమణ సౌష్ఠవం : ఒక పటమును దాని మధ్య బిందువు గుండా కొంత కోణంతో భ్రమణం చేయగా ఏర్పడు పటం మొదటి పటం వలె అదే విధంగా ఉన్నచో ఆ పటం భ్రమణ సౌష్ఠవం కలిగి ఉంది అంటారు. ఈ స్థిర మధ్యబిందువును “భ్రమణ కేంద్రం” అంటారు. ఇలా పటాన్ని భ్రమణం చేయునపుడు ఏ కనిష్ఠ కోణానికి అదే పటంలో ఏకీభవిస్తుందో ఆ కోణమే ఆ పటం యొక్క “భ్రమణ సౌష్ఠవ కోణం” అవుతుంది. పై విధంగా భ్రమణం చేయునపుడు 360° (అనగా, పూర్తి భ్రమణంలో)ల భ్రమణంలో పటం ఎన్నిసార్లు అదే పటంలో ఏకీభవిస్తుందో అదే ఆ పటం యొక్క భ్రమణ సౌష్ఠవ పరిమాణం.
భ్రమణ సౌష్ఠవ పరిమాణం = \(\frac{360^{\circ}}{x^{\circ}}\)
ఇక్కడ x° = భ్రమణ సౌష్ఠవ కోణము.