Students can go through AP Board 7th Class Maths Notes 1st Lesson పూర్ణ సంఖ్యలు to understand and remember the concept easily.
AP Board 7th Class Maths Notes 1st Lesson పూర్ణ సంఖ్యలు
→ క్రీ.శ. 7వ శతాబ్దములోనే భారతీయ గణిత శాస్త్రవేత్త బ్రహ్మగుప్తుడు తన పుస్తకమైన ‘బ్రహ్మస్పుట సిద్ధాంతము’ నందు ఋణసంఖ్యల లబ్ధములను మొదటిసారిగా ప్రస్తావించాడు. ఇతను ఒక సంఖ్య మరియు వాటి వర్గాలతో కూడిన సమస్యల సూత్రీకరణకు ఒక సాధారణ పద్ధతి ఇవ్వడానికి మరియు వాటి సాధన కనుగొనుటకు ఋణసంఖ్యను ఋణసంఖ్యతో గుణించిన లబ్ధము ధనసంఖ్య అని నిర్వచించాడు.
→ సహజ సంఖ్యలు (1, 2, 3, 4, 5, …..), సున్న (0) మరియు ఋణ సంఖ్యలు (-1, -2, -3, -4, -5, ….) లను కలిపి పూర్ణసంఖ్యలు అంటారు.
→ రెండు ధన పూర్ణ సంఖ్యల లేదా రెండు ఋణ పూర్ణ సంఖ్యల లబ్దము ఒక ధన పూర్ణ సంఖ్య.
→ ఒక ధన పూర్ణ సంఖ్య మరియు ఋణ పూర్ణ సంఖ్యల లబ్దము ఋణ పూర్ణ సంఖ్య.
→ రెండు ధన పూర్ణ సంఖ్యల లేదా రెండు ఋణ పూర్ణ సంఖ్యల భాగఫలం ఒక ధన పూర్ణ సంఖ్య.
→ ఒక ధన పూర్ణ సంఖ్య మరియు ఋణ పూర్ణ సంఖ్యల భాగఫలం ఒక ఋణ పూర్ణ సంఖ్య.
![]()
→ పూర్ణ సంఖ్యల ధర్మాలు:
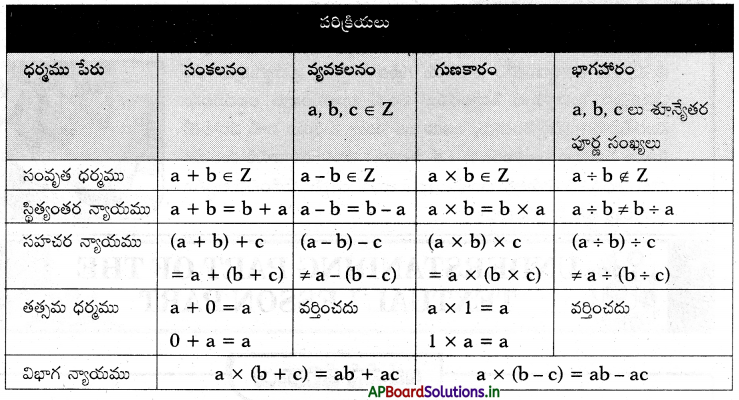
→ సంఖ్యా సమాసాలను సూక్ష్మీకరించుటకు, మనం తప్పనిసరిగా BODMAS నియమము (బ్రాకెట్స్, ఆఫ్, భాగహారము, గుణకారము, సంకలనము, వ్యవకలనము) ను అనుసరించాలి.
→ సంఖ్యా సమాసాల సూక్ష్మీకరణలో బ్రాకెటు విన్కులం బ్రాకెట్, సాధారణ బ్రాకెట్, కర్లీ బ్రాకెట్, చతురస్ర బ్రాకెట్ క్రమములో పూర్తి చేయాలి. అనగా [{{-}}] లను లోపలినుండి బయటకు క్రమములో పూర్తిచేయాలి.
→ ఒక పూర్ణ సంఖ్య యొక్క సంఖ్యా విలువ (దాని గుర్తును పరిగణనలోకి తీసుకోకుండా)ను దాని యొక్క పరమ మూల్యము అంటారు. ఒక సంఖ్య యొక్క పరమ మూల్యము ఎల్లప్పుడూ రుణాత్మకం కాదు.
→ సహజ సంఖ్యలు (N) = {1, 2, 3, 4, 5, 6, ……………..}
→ పూర్ణాంకాలు (W) = {0, 1, 2, 3, 4, 5, ………………..
→ పూర్ణసంఖ్యలు (Z): సహజసంఖ్యలు (N), సున్నా {0} మరియు రుణ సంఖ్యలు {-1, -2, -3, – 4, – 5, ……. } లను కలిపి పూర్ణసంఖ్యలు అంటారు.
Z = {…….. – 5, – 4, – 3, -2, – 1, 0, 1, 2, 3, 4, …………}
→ ఏవైనా రెండు పూర్ణసంఖ్యలు a, b లకు (-a) × b = – (a × b) = a × (-b)
→ రెండు పూర్ణసంఖ్యలు ఒకే గుర్తు కలిగి ఉంటే వాటి లబ్దము “ధన పూర్ణసంఖ్య” అవుతుంది.
ఉదా:
- 2 × 3 = 6
- (-2) × (-3) = 6
![]()
→ రెండు పూర్ణ సంఖ్యలు వేరు, వేరు గుర్తులు కలిగి ఉంటే వాటి లబ్దము రుణ పూర్ణ సంఖ్య అవుతుంది.
ఉదా:
(i) 2 × ( 3) = -6
(ii) (-2) × 3 = -6
- ధన పూర్ణసంఖ్య × ధన పూర్ణ సంఖ్య = ధన పూర్ణసంఖ్య
- ధన పూర్ణసంఖ్య × రుణ పూర్ణ సంఖ్య = రుణ పూర్ణ సంఖ్య
- రుణ పూర్ణ సంఖ్య × ధన పూర్ణ సంఖ్య = రుణ పూర్ణ సంఖ్య
- రుణ పూర్ణ సంఖ్య × రుణ పూర్ణ సంఖ్య = ధన పూర్ణ సంఖ్య
→ ఒకే గుర్తుగల రెండు పూర్ణ సంఖ్యల భాగఫలము ధనాత్మకం.
- 12 + 3 = 4
- (-12) + (-3) = 4
→ వేరు వేరు గుర్తుగల రెండు పూర్ణ సంఖ్యల భాగఫలము రుణాత్మకం.
(i) (- 12) + 3 =-4
(ii) 12 + (-3) = – 4
- ధన పూర్ణసంఖ్యను, ధన పూర్ణసంఖ్యతో భాగించిన భాగఫలం ధనాత్మకం. 12 + 3 = 4
- రుణ పూర్ణసంఖ్యను, ధన పూర్ణసంఖ్యతో భాగించిన భాగఫలం రుణాత్మకం. (-12) + 3 = -4
- ధన పూర్ణసంఖ్యను, రుణ పూర్ణసంఖ్యతో భాగించిన భాగఫలం రుణాత్మకం. 12 + (-3) = -4
- రుణ పూర్ణసంఖ్యను, రుణ పూర్ణసంఖ్యతో భాగించిన భాగఫలం ధనాత్మకం. (-12) + (-3) = 4
→ BODMAS నియమము: అంకగణిత వివిధ పరిక్రియలను పూర్తిచేయాల్సిన క్రమాన్ని తెలిపే నియమమే BODMAS
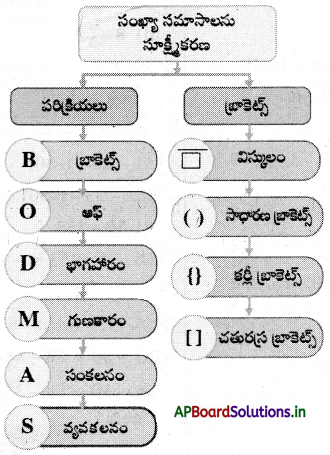
![]()
→ పరమ మూల్యము: ఒక పూర్ణ సంఖ్య యొక్క సంఖ్యా విలువ (దాని గుర్తును పరిగణనలోకి తీసుకోకుండా)ను దాని పరమ మూల్య విలువ అంటారు. పరమ మూల్య విలువ ఎల్లప్పుడూ రుణాత్మకం కాదు. x యొక్క పరమ మూల్యమును |x| తో సూచిస్తాము.
- x > 0 అయిన |x| = x
- x < 0 అయిన |x| = -x
- x = 0 అయిన |x| = 0