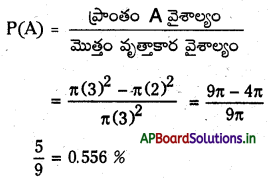Students can go through AP Board 9th Class Maths Notes 14th Lesson సంభావ్యత to understand and remember the concept easily.
AP Board 9th Class Maths Notes 14th Lesson సంభావ్యత
→ మన నిత్యజీవితంలో సంభవించు సంఘటలను మాపనము చేయుటకు ఉపయోగపడు అధ్యాయము “సంభావ్యత”.
→ నిత్యజీవితంలో మనం ఏదైన ఒక విషయం జరిగే అవకాశాలను వ్యక్తీకరించుటకు, అధిక సంభవం, అసంభవం, ‘అల్ప సంభవం వంటి పదాలను ఉపయోగిస్తాము.
→ కొన్ని ప్రయోగాలతో పర్యవసానాలన్నీ ముందే తెలిసినప్పటికీ, ప్రయోగం చేసే సమయంలో ఏ పర్యవసానం ఏర్పడుతుందో ముందుగానే ఊహించలేము. అటువంటి ప్రయోగాలను “యాదృచ్చిక ప్రయోగాలు” అంటాము.
ఉదా : నాణేన్ని ఎగురవేయుట, పాచికను దొర్లించుట, పేక ముక్కల కట్ట నుండి ఒక కార్డును తీయుట.
→ ఒకసారి నాణేన్ని ఎగురవేసిన లేదా పాచికను దొర్లించిన దానిని యత్నం (Trial) (లేక) యాదృచ్ఛిక ప్రయోగం అని అంటారు.
→ ఒక యాదృచ్ఛిక ప్రయోగం యొక్క ప్రతి పర్యవసానాన్ని ఘటన (event) అని అంటారు.
→ అవకాశాలను మాపనం చేయుటకు ముందు వాటిని కింది విధంగా శ్రేణీకరిస్తాము.
- నిశ్చితం (కచ్చితం) : ఏదైనా విషయం తప్పకుండా జరిగే అవకాశం.
- అధిక సంభవం : ఏదైనా విషయం జరిగే అవకాశం చాలా ఎక్కువ.
- సమ సంభవం : కొన్ని విషయాలు జరిగేటందుకు సమాన అవకాశాలు ఉండుట.
- అల్ప సంభవం : ఏదైనా విషయం జరిగే అవకాశం చాలా తక్కువ.
- అసంభవం : ఏదైనా విషయం జరిగే అవకాశం శూన్యము.
![]()
→ ఘటన యొక్క సంభావ్యత
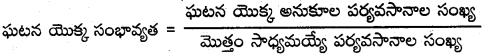
→ కచ్చితమైన ఘటన సంభావ్యత = 1
→ అసంభవం అయిన ఘటన సంభావ్యత = 0
→ ఒక ఘటన యొక్క సంభావ్యత ‘0’ మరియు ‘1’ ల మధ్య ఉండును. (0 మరియు 1 కలిపి).
ఉదాహరణ – 1:
రెండు నాణాలను (ఒకే విధంగా ఉండే) ఒకేసారి పైకి ఎగురవేసిన
(a) సాధ్యమయ్యే పర్యవసానాలు
(b) సాధ్యమయ్యే పర్యవసానాల సంఖ్య
(c) రెండూ బొమ్మలు వచ్చే సంభావ్యత
(d) కనిష్ఠంగా ఒక బొమ్మ వచ్చే సంభావ్యత
(e) బొమ్మ పడని సంభావ్యత మరియు
(f) ఒకే ఒక బొమ్మపడే సంభావ్యతలను కనుక్కోండి.
జవాబు :
a) సాధ్యమయ్యే పర్యవసానాలు
| 1వ నాణెం | 2వ నాణెం |
| బొమ్మ | బొమ్మ |
| బొమ్మ | బొరుసు |
| బొరుసు | బొమ్మ |
| బొరుసు | బొరుసు |
b) మొత్తం పర్యవసానాల సంఖ్య 4 .
c) రెండూ బొమ్మ వచ్చే సంభావ్యత రెండు బొమ్మలు వచ్చే అనుకూల పర్యవసానాల సంఖ్య మొత్తం సాధ్యమయ్యే పర్యవసానాల సంఖ్య

d) కనీసం ఒక బొమ్మపడే సంభావ్యత = \(\frac{3}{4}\)
(కనీసం ఒక బొమ్మ అనగా ఒకటి లేదా అంతకన్నా ఎక్కువ బొమ్మలు).
e) బొమ్మలేని పర్యవసానాల సంభావ్యత = \(\frac{1}{4}\)
f) ఒకే ఒక్క బొమ్మ ఉండే పర్యవసానాల సంభావ్యత = \(\frac{2}{4}=\frac{1}{2}\)
ఉదాహరణ – 2:
ఒక పాచికను దొర్లించినప్పుడు
(a) దాని పైముఖంపై వచ్చే ప్రతి అంకె యొక్క సంభావ్యతను ‘పట్టికలో రాయండి.
(b) అన్ని సాధ్యమయ్యే పర్యవసానాల సంభావ్యతల మొత్తం కనుక్కోండి.
సాధన.
a) పాచికను దొర్లించినప్పుడు సాధ్యమయ్యే మొత్తం ఆరు పర్యవసానాల్లో 4 అంకె ఒకసారి రావడానికి సాధ్యము కావు. సంభావ్యత 1/6.

b) అన్ని పర్యవసానాల సంభావ్యతల మొత్తం
P(1) + P(2) + P(3) + P(4) + P(5) + P(6)
= \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\) = 1
ఉదాహరణ -3:
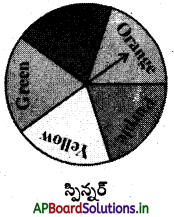
ఒక స్పిన్నర్ (గుండ్రంగా తిప్పేందుకు వీలైన చక్రం) 1000 సార్లు తిప్పడం జరిగింది. ప్రతిసారి తిప్పినప్పుడు పాచిక ఆగే ప్రదేశం యొక్క రంగు పట్టికలో రాసినప్పుడు, వాటి పౌనఃపున్యం కింది విధంగా ఉంది.

a) స్పిన్నర్ నుండి సాధ్యమయ్యే పర్యవసానాలు ఎన్ని ? అవి ఏవి ?
b) ప్రతి రంగు పర్యవసానంగా వచ్చే సంభావ్యత కనుగొనండి. .
c) పట్టిక నుండి, ప్రతి రంగు యొక్క పౌనఃపున్యానికి, మొత్తం పౌనఃపున్యానికి నిష్పత్తిని కనుగొనండి.
జవాబు :
a) స్పిన్నర్ చూసినప్పుడు 5 సెక్టర్లు ఒకే వైశాల్యం గల ప్రదేశాలుగా ఉన్నాయి. ఇవన్నియూ 5 వేరు వేరు రంగులలో కలవు. అవి ఎరుపు, నారింజ, వంగపండు, పసుపు, ఆకుపచ్చ ఇవన్నియూ సమసంభవం కల్గిన పర్యవసానాలు. మొత్తం పర్యవసానాల సంఖ్య 5.
b) ప్రతి ఘటన యొక్క సంభావ్యత,
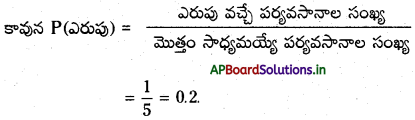
ఇదే విధంగా P (నారింజ), P (వంగపండు), P (పసుపు) మరియు P (ఆకుపచ్చ) మరియు \(\frac{1}{5}\) లేదా 0.2.
c) పట్టిక నుండి 1000 సార్లు స్పిన్నర్ తిప్పినపుడు 185 సార్లు ఎరుపుకు అనుకూలంగా ఉంది. ప్రయోగాలలో ఎరుపు రంగు పౌనఃపున్యం
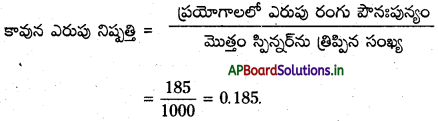
ఈ విధంగా మిగిలిన రంగులకి కూడా ఈ విధమైన నిష్పత్తులను రాసిన నారింజ, వంగపండు, పసుపు, ఆకుపచ్చలకు వరుసగా 0. 195, 0.210, 0.206 మరియు 0.204 వచ్చింది.
(b), (C) లను పరిశీలించిన (C) లో కనుగొన్న నిష్పత్తులన్నీ (b) లోని ఆయారంగుల సంభావ్యతలకు దగ్గరగా ఉన్నాయి. అంటే మనం కనుగొన్న సంభావ్యత, ప్రయోగం తర్వాత కనుగొన్న నిష్పత్తులకు దాదాపు సమానంగా ఉన్నాయి.
![]()
ఉదాహరణ – 4:
ఒక సినిమా థియేటర్ కి విచ్చేసిన ప్రేక్షకుల సంఖ్య వయసుల వారీగా ఇవ్వబడ్డాయి. బంపర్ బహుమతి గెలుచుకోవడానికి ప్రతి ప్రేక్షకుడికి టికెట్టుతోపాటు ఒక నెంబరు ఈయబడింది. నెంబర్లలో నుండి యాదృచ్ఛికంగా ఒక నెంబరును తీసినప్పుడు, కింద నీయబడిన ఘటనలకు సంభావ్యత కనుగొనండి.
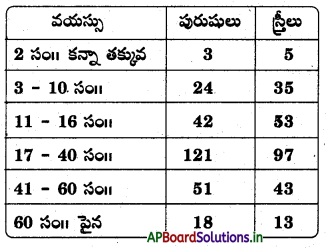
మొత్తం ప్రేక్షకుల సంఖ్య = 505.
జవాబు :
a) వయసు 10 గాని అంతకంటే తక్కువగాని ఉన్న ప్రేక్షకుడి సంభావ్యత 10 గాని అంతకంటే తక్కువ వయసు ఉన్న ప్రేక్షకులు
= 24 + 35 + 5 + 3 = 67
మొత్తం ప్రేక్షకుల సంఖ్య = 505
P (క్షకుని వయసు < 10 సంవత్సరాలు) = \(\frac{67}{505}\)
b) వయసు 16 గాని అంతకంటే తక్కువగాని ఉన్న స్త్రీ ప్రేక్షకుల సంభావ్యత వయస్సు 16 గాని అంతకంటే తక్కువగాని ఉన్న స్త్రీ ప్రేక్షకులు = 53 + 35 + 5 = 93
P (స్త్రీ ప్రేక్షకుల వయసు ≤ 16 సంవత్సరాలు) = \(\frac{93}{505}\)
c) వయసు 17 గాని అంతకంటే ఎక్కువగాని ఉన్న పురుష ప్రేక్షకుల సంభావ్యత వయస్సు 17 గాని. అంతకంటే ఎక్కువగాని ఉన్న పురుష ప్రేక్షకులు = 121 + 51 + 18 = 190
P (పురుష ప్రేక్షకుల వయసు ≥ 17 సంవత్సరాలు) = \(\frac{190}{505}=\frac{38}{101}\)
d) వయసు 40 సం||రాలు పైబడిన ప్రేక్షకుల సంభావ్యత వయసు 40 సం||రాలు పైబడిన,
ప్రేక్షకుల సంభావ్యత = 51 + 43 + 18+ 13 = 125 .
P (ప్రేక్షకుల వయసు > 40 సంవత్సరాలు)
= \(\frac{125}{505}=\frac{25}{101}\)
e) పురుషులు కాకుండా ఉన్న ప్రేక్షకుల సంభావ్యత . పురుషులు కాకుండా ఉన్న ప్రేక్షకులు
= 5+ 35 + 53 + 97 + 43 + 13 = 246
P (పురుషుడు కాని ప్రేక్షకుల సంఖ్య) = \(\frac{246}{505}\)
ఉదాహరణ – 5:
మూడు ఏకకేంద్ర. వృత్తాకారాలతో (వ్యాసార్ధాలు వరుసగా 3 సెం.మీ, 2 సెం.మీ. మరియు 1 సెం.మీ.) తయారుచేయబడిన ఒక డార్ట్ బోర్డు A, B మరియు C అనే ప్రాంతాలుగా విభజింపబడింది (పటం చూడండి). మొనతేలిన ఒక బల్లెం (dart) ను బోర్డుపైకి విసిరిన అది ప్రాంతం A లో తగిలే సంభావ్యత ఎంత ? A అనేది (బయట కంకణాకార ప్రాంతం).
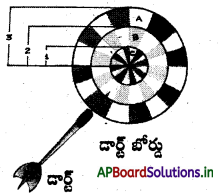
జవాబు :
A ప్రాంతంలో తగిలే ఘటన యొక్క సంభావ్యత.
మొత్తం వృత్తాకార ప్రాంత వైశాల్యం (వ్యాసార్ధం 3 సెం.మీ.తో) = π (3)2
కంకణ ప్రాంతం (A) వైశాల్యం = π (3)2 – π (2)2
బల్లెం కంకణ ప్రాంతం (A) లో తగిలే సంభావ్యత P(A)
వృత్త వైశాల్యం = πr2
కంకణ వైశాల్యం = πR2 – πr2
అని గుర్తుకు తెచ్చుకోండి.