Students can go through AP Board 9th Class Maths Notes 13th Lesson జ్యామితీయ నిర్మాణాలు to understand and remember the concept easily.
AP Board 9th Class Maths Notes 13th Lesson జ్యామితీయ నిర్మాణాలు
→ జ్యా మితీయ నిర్మాణంలో మనము ముఖ్యముగా రెండు పరికరాలను వినియోగిస్తాము. అవి :
- కొలతలు లేని కొలబద్ద
- వృత్తలేఖిని.
→ (i) దత్త రేఖాఖండానికి లంబసమద్విఖండన రేఖ గీయుట.
(ii) దత్తకోణానికి సమద్విఖండన రేఖ గీయుట.
(iii)మూల. బిందువు వద్ద, దత్త కిరణంపై 60° కోణం హేతుబద్ధంగా నిరూపించుట.
![]()
→ భూమి, భూకోణం మరియు మిగిలిన రెండు భుజాల మొత్తం ఇచ్చినపుడు త్రిభుజంను నిర్మించవచ్చును.
→ భూమి, భూకోణం మరియు రెండు భుజాల మధ్య భేదం ఇచ్చిన త్రిభుజంను నిర్మించవచ్చును.
→ త్రిభుజ చుట్టుకొలత మరియు రెండు భూకోణాలు ఇచ్చినపుడు త్రిభుజంను నిర్మించవచ్చును. , దత్త జ్యా, దత్త కోణాన్ని కలిగివుండే వృత్తఖండాన్ని నిర్మించవచ్చును.
ఉదాహరణ – 1:
AB అనే దత్తరేఖా ఖండానికి లంబ సమద్విఖండన రేఖను గీచి, నిర్మాణాన్ని తార్కికంగా సమర్థించుము.
జవాబు :
నిర్మాణ సోపానాలు :
సోపానం – 1: దత్త రేఖాఖండం AB ను గీయండి.
సోపానం – 2 : కేంద్రాలుగా కన్నా ఎక్కువ వ్యాసార్ధంతో రేఖాఖండానికి ఇరువైపులా రెండు చాపములు ఒకదానికొకటి ఖండించుకునేటట్లు గీయాలి.
సోపానం – 3 : ‘B’ కేంద్రముగా, అదే వ్యాసార్ధంతో మరి రెండు చాపములను మొదటి చాపములు ఖండించునట్లు గీయాలి.
సోపానం – 4 : ఖండన బిందువులకు P మరియు Q అని పేర్లు పెట్టి P, QQ లను కలపాలి.
సోపానం – 5 : AB యొక్క లంబ సమద్విఖండన రేఖ PQ” అనే నిర్మాణాన్ని నీవు ఏ విధంగా సమర్థించగలవు ?
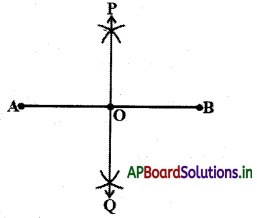
POQ రేఖ AB కి లంబసమద్విఖండన రేఖ అవుతుంది.
పై నిర్మాణ క్రమము నుండి AB రేఖకు, “PQ ఒక లంబ సమద్విఖండన రేఖ” అవుతుంది అని కారణాలతో ఎలా భావించగలవు ?
నిర్మాణం యొక్క పటంను గీచి, A ను P, Qలతోనూ, B ను P మరియు Qలతోనూ కలపాలి.
త్రిభుజ సర్వసమాన నియమాల ఆధారంగా మనం ఈ ప్రవచనాన్ని నిరూపిస్తాం.
ఉపపత్తి :
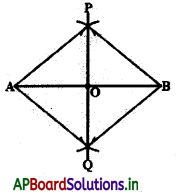
| సోపానాలు | కారణాలు |
| ∆sPAQ మరియు ∆PBQ లో | (తీసుకున్న త్రిభుజాలు) |
| AP = BP; AQ = BQ | (సమాన వ్యాసార్ధాలు) |
| PQ = PQ | (ఉమ్మడి భుజం) |
| ∴ ∆PAQ = ∆PBQ | (భు.భు.భు. నియమం) |
| కావున ∠APO = ∠BPO | (సర్వసమాన త్రిభుజాలలో సదృశ భాగాలు సమానం) |
| ఇప్పుడు, ∆<sup>2</sup>APO మరియు BPO లలో | (తీసుకున్న త్రిభుజాలు) |
| AP = BP | (ముందు తీసుకున్నట్లు సమాన వ్యాసార్ధాలు) |
| ∠APO = ∠BPO | (నిరూపించబడింది) |
| OP = OP | (ఉమ్మడి భుజం) |
| ∴ ∆APO ≅ ∆BPO | (భు. కో. భు. నియమం ప్రకారం) |
| కావున OA = OB మరియు ∠APO = ∠BPO | (సర్వ సమాన త్రిభుజాలలో సదృశ్య భాగాలు సమానం) |
| కాని ∠AOP + ∠BOP = 180° | (రేఖీయద్వయం) |
| అందుచే ∠AOP = ∠BOP = \(\frac{180^{\circ}}{2}\) = 90° | (పై సోపానం ఆధారంగా ఫలితం) |
కావున PO అంటే POQ రేఖ AB రేఖాఖండానికి లంబసమద్విఖండన రేఖ అయినది. నిరూపించబడినది.
ఉదాహరణ -2:
దత్తకోణం ∠ABC కి సమద్విఖండన రేఖను గీయండి.
సాధన.
నిర్మాణ సోపానాలు :
సోపానం – 1 : దత్తకోణం ∠ABC ని తీసుకొనుము.
సోపానం – 2 : B కేంద్రంగా కొంత వ్యాసార్ధంతో BA, BC కిరణాలను
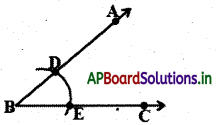
D, E ల మధ్య ఖండించునట్లు పటంలో చూపినట్లు చాపం గీయండి.
సోపానం – 3 : E మరియు D లు కేంద్రములుగా సమాన వ్యాసార్థంతో ఆ రెండు చాపములు F వద్ద ఖండించునట్లు గీయండి.
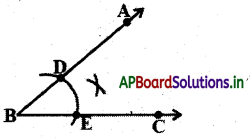
సోపానం – 4 : BF కిరణంను గీయండి. ఇదే ∠ABC కి కోణ సమద్విఖండన రేఖ అగును.
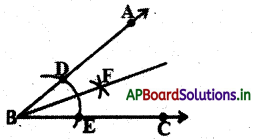
పై నిర్మాణాన్ని తార్కికంగా నిరూపించిన విధం పరిశీలిద్దాం. D, F మరియు E, F లను కలపండి. త్రిభుజ సర్వసమాన నియమాలను బట్టి కింది విధంగా నిరూపిద్దాం
ఉపపత్తి :
| సోపానాలు | కారణాలు |
| ∆sBDF మరియు ∆BEF లలో | (తీసుకున్న త్రిభుజాలు) |
| BD = BE | (గీచిన చాపాల వ్యాసార్ధాలు సమానం) |
| DF = EF | (సమాన వ్యాసార్ధాలు) |
| BF = BF. | (ఉమ్మడి భుజం) |
| ∴ ∆BDF ≅ ∆BEF | (భు.భు.భు. నియమం) |
| కావున ∠DBF = ∠EBF | (సర్వసమాన త్రిభుజాలలో సదృశ భాగాలు) |
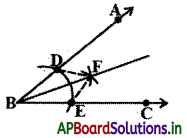
కావున BF అనేది ∠ABC యొక్క సమద్విఖండన రేఖ అయినది. నిరూపించబడినది.
![]()
ఉదాహరణ -3:
తొలి బిందువు A నుండి AB కిరణం గీచి, ∠BAC = 60° అగునట్లు AC కిరణాన్ని గీయండి.
సాధన.
నిర్మాణ సోపానాలు :
సోపానం – 1: AB కిరణాన్ని గీచి కొంత వ్యాసార్ధంతో A కేంద్రంగా AB ను D వద్ద ఖండించునట్లు ఒక చాపం గీయండి.
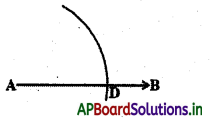
సోపానం – 2 : D కేంద్రంగా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని E వద్ద ఖండించునట్లు మరొక చాపాన్ని గీయాలి. (పటంలో చూపిన విధంగా)
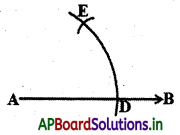
సోపానం – 3 : E గుండా పోతున్నట్లుగా AC కిరణాన్ని గీస్తే మనకు కావలసిన కోణం ∠BAC = 60° వస్తుంది.
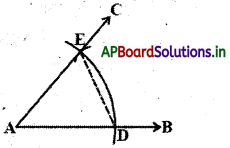
మనం చేసిన నిర్మాణంను నిరూపించాలంటే పటంలో D, E ని కలపాలి. నిరూపణను దిగువ విధంగా చేయవచ్చు.
ఉపపత్తి :
| సోపానాలు | కారణాలు |
| ∆ADE లో | (ఒకే వృత్త వ్యాసార్ధాలు) |
| AE = AD | (నిర్మాణంలో తీసుకోబడినది) |
| AD = DE | (సమాన వ్యాసార్ధాలు గల చాపాలు) |
| అందుచే AE = AD = DE | (సమాన చాపాలతో ఏర్పడిన భాగాలు) |
| కావున ∆ADE ఒక సమబాహు త్రిభుజం అగును. | (అన్ని భుజాలు సమానం) |
| ∴ ∠EAD = 60° | (సమబాహు త్రిభుజంలో ప్రతీకోణం) |
| ∠BAC = ∠EAD | (∠EAD అనేది ∠BAC లో ఒక భాగం) |
| ∴ ∠BAC = 60. | ఈ విధంగా నిరూపించబడినది. |
ఉదాహరణ -4:
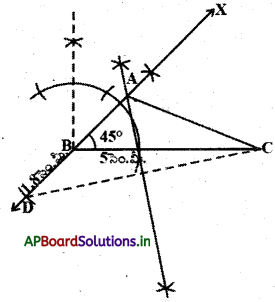
BC = 5 సెం.మీ., AB + AC = 8 సెం.మీ. మరియు ∠ABC = 60° కొలతలలో AABC నిర్మించండి.
సాధన.
నిర్మాణ సోపానాలు :
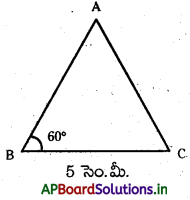
సోపానం – 1: ∆ABC చిత్తు పటంను గీచి ఇవ్వబడిన కొలతలు గుర్తించాలి. (AB + AC = 8 సెం.మీ. కొలతను ఎందుకు గుర్తించలేకపోయారు ?) . మరి త్రిభుజ మూడవ శీర్షం Aను నిర్మాణంలో ఎలా గుర్తిస్తారు ?
విశ్లేషణ : AB + AC = 8 సెం.మీ. కావున BA ను D వరకు పొడిగిస్తే
BD = 8 సెం.మీ. అవుతుంది.
∴ BD = BA + AD = 8 సెం.మీ.
కాని AB + AC = 8 సెం.మీ. (దత్తాంశం)
∵ AD = AC
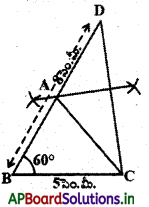
BD పైన Aను గుర్తించడానికి మీరు ఏమి చేస్తారు ?
A బిందువు C మరియు D లకు సమాన దూరంలో ఉంటుంది. కావున, \(\overline{\mathrm{CD}}\) యొక్క లంబ సమద్విఖండన BD ను ఖండించే బిందువు A అవుతుంది.
సోపానం – 2 : BC = 5 సెం.మీ. (త్రిభుజం భూమి) రేఖాఖండం గీచి B వద్ద 2∠CBX = 60°కోణం నిర్మించాలి.
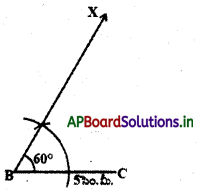
సోపానం – 3 : B కేంద్రంగా 8 సెం.మీ. (AB + AC = 8 సెం.మీ.) BXను D వద్ద ఖండించునట్లు ఒక చాపం గీయాలి.
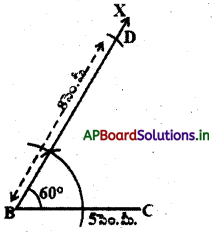
సోపానం – 4 : CD ని కలిపి CD కు లంబ సమద్విఖండన రేఖను గీస్తే అది BD ని A.వద్ద ఖండిస్తుంది.
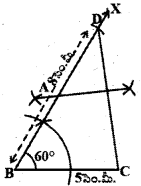
సోపానం – 5 : AC లను కలిపితే మనకు కావల్సిన ABC త్రిభుజం వస్తుంది. మనం ఇప్పుడు నిర్మాణాన్ని నిరూపిద్దాం.
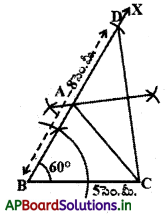
ఉపపత్తి : A బిందువు CD యొక్క లంబసమద్విఖండన రేఖపై ఉంది.
∵ AC = AD కావున
AB + AC = AB + AD = BD = 8 సెం.మీ.
అందుచే AABC మనకు కావల్సిన త్రిభుజం అయింది.
![]()
ఉదాహరణ -5:
BC = 4.2 సెం.మీ., ∠B = 30° మరియు AB – AC = 1.6 సెం.మీ. కొలతలతో ∆ABC నిర్మించండి.
సాధన.
నిర్మాణ సోపానాలు :
సోపానం – 1: ∆ABC యొక్క చిత్తుపటం గీచి ఇవ్వబడిన కొలతలను గుర్తించాలి. (AB – AC = 1.6 సెం.మీ. కొలతను ఎలా గుర్తిస్తారు ?)
విశ్లేషణ : AB – AC = 1.6 సెం.మీ. కావున AB > AC అగును.
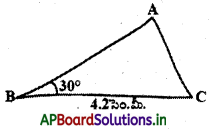
AD = AC అగునట్లు AB పై D అని బిందువును గుర్తించాలి.
ఇప్పుడు BD = AB – AC = 1.6 సెం.మీ.
అందుచే C, D ని కలిపి దానికి లంబసమద్విఖండన చేస్తే మూడవ శీర్షం A ను BD పై గుర్తించవచ్చును.
అవసరమైతే BD ని పొడిగించాలి. A, C ని కలిపితే .
కావలసిన త్రిభుజం ABC వస్తుంది.
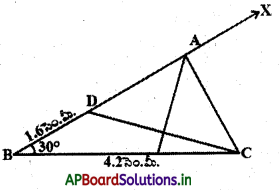
సోపానం – 2 : భు.కో.భు. త్రిభుజ నియమం అనుసరించి , BC = 4.2 సెం.మీ., ∠B = 30° మరియు BD = 1.6 సెం.మీ. (i.e AB – AC) ∆BCD ని నిర్మించాలి.
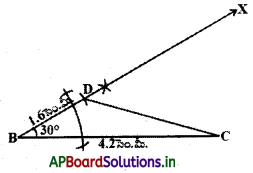
సోపానం – 3 : CP యొక్క లంబ సమద్విఖండన రేఖను గీస్తే అది BDX రేఖను A వద్ద ఖండిస్తుంది.
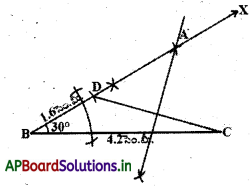
సోపానం – 4 : A, C లను కలిపితే AABC వస్తుంది.
ఉదాహరణ – 6:
BC = 5 సెం.మీ., ∠B = 45° మరియు AC – AB = 1.8 సెం.మీ. కొలతలతో ∆ABC నిర్మించండి.
సాధన.
నిర్మాణ సోపానాలు :
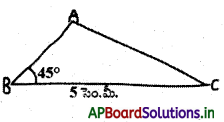
సోపానం – 1: ∆ABC యొక్క చిత్తుపటాన్ని గీచి ఇచ్చిన కొలతలు గుర్తించాలి.
AC – AB = 1.8 సెం.మీ. కొలతను ఎలా గుర్తించగలరో విశ్లేషణ చేయండి.
విశ్లేషణ : AB < AC కావున AC – AB = 1.8 సెం.మీ. ను BD గా
తీసుకోవాలంటే, AD = AC అయినట్లు AC పై D బిందువును గుర్తించండి.
ఇప్పుడు BD = AC – AB = 1.8 అగును. (∵ BD = AD – AB మరియు AD = AC)
C, D ని కలిపి CD కి లంబసమద్విఖండన రేఖను గీస్తే దానిపై A ను గుర్తించవచ్చు.
సోపానం – 2 : BC = 5 సెంమీ. రేఖాఖండం గీచి, ∠CBX = 45° కోణం నిర్మించాలి. B కేంద్రంగా 1.8 సెం.మీ. వ్యాసార్ధంతో (BD = AC – AB) ఒక చాపం గీయగా అది BX రేఖను BC కి ఎదురుగా పొడిగిస్తే దానిని D వద్ద ఖండిస్తుంది.
సోపానం – 3: D, C ని కలిపి దానికి లంబ సమద్విఖండన రేఖ గీయాలి.
సోపానం – 4 : ఇది BX రేఖను A వద్ద ఖండిస్తుంది. AC ని కలిపితే మనకు కావలసిన త్రిభుజం ∆ABC వస్తుంది.
ఇప్పుడు మనం పై నిర్మాణంను తార్కికంగా నిరూపిద్దాం.
విశ్లేషణ : ∆ABC లో భూమి BC R, ∠B కోణాన్ని నిర్మించాం.
DC యొక్క లంబసమద్విఖండన రేఖపై A బిందువు ఉన్నది కావున
∴ AD = AC అగును.
అంటే, AB + BD = AC
కావున BD = AC – AB అయినది.
= 1.8 సెం.మీ.
ఇదే మనకు కావలసిన త్రిభుజం AABC అవుతుంది.
ఉదాహరణ -7:
∆ABC లో. ∠B = 609, ∠C = 45° మరియు .. AB + BC + CA = 11 సెం.మీ. అయిన త్రిభుజం నిర్మించండి.
సాధన:
నిర్మాణ సోపానాలు :
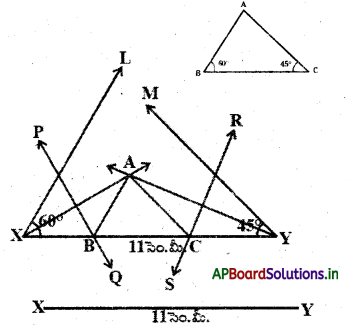
సోపానం – 1: ∆ABC త్రిభుజం యొక్క చిత్తుపటంను గీచి ఇవ్వబడిన కొలతలు గుర్తించాలి. (త్రిభుజ చుట్టుకొలతను ఎలా గుర్తిస్తారు ?)
విశ్లేషణ : త్రిభుజం చుట్టుకొలత AB + BC + CA కు సమానమయ్యే
రేఖాఖండం XY గీయాలి. ∠B కు సమానంగా 4YXL నూ, ∠C కు సమానం అయ్యేటట్లు ∠XYM ను నిర్మించి,
వాటిని సమద్విఖండన చేయాలి. ఈ రెండు సమద్విఖండన రేఖలు A వద్ద ఖండించుకున్నాయనుకోండి. AX యొక్క లంబసమద్విఖండన రేఖ XY ను B వద్ద,
AY యొక్క లంబసమద్విఖండన రేఖ C వద్ద ఖండిస్తాయి.
AB, AC లను కలిపితే మనకు కావలసిన త్రిభుజం ABC వస్తుంది.
సోపానం – 2 : XY = 11 సెం.మీ. (ఎందుకంటే XY = AB + BC + CA) రేఖాఖండాన్ని గీయాలి.
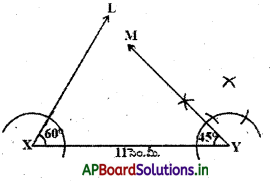
సోపానం – 3 : ∠YXL = 60° మరియు ∠XYM = 45° కోణాలను నిర్మించి, వాటికి సమద్విఖండన రేఖలు గీయాలి.
సోపానం – 4 : ఈ రెండు సమద్విఖండన రేఖల ఖండన బిందువుకు A అని పేరు పెట్టాలి.
సోపానం – 5 : AX మరియు AY లకు లంబసమద్విఖండన L రేఖలను గీస్తే అవి XY ను వరుసగా B మరియు C ల వద్ద ఖండిస్తాయి.
AB మరియు AC లను కలపాలి. మనకు కావల్సిన త్రిభుజం ABC వస్తుంది. ఈ నిర్మాణంను మనం కింది విధంగా నిరూపిద్దాం.
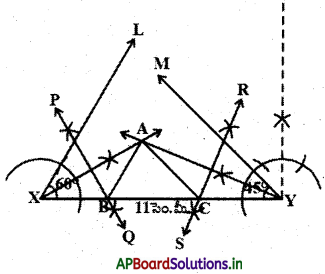
ఉపపత్తి : AX యొక్క లంబ సమద్విఖండన రేఖ PQ పై B ఉంటుంది.
∴ XB = AB మరియు అదేవిధంగా CY = AC.
దీని నుండి AB + BC + CA = XB + BC + CY = XY తిరిగి ∠BAX = ∠AXB (∴ ∆AXB లో XB = AB) మరియు ∠ABC = ∠BAX + ∠AXB (AABC యొక్క బాహ్యకోణం)
= 2∠AXB.: ∠YXL = 60° ఇదే విధంగా
∠ACB = ∠XYM = 45° అగును.
∴ ∠B = 60° మరియు ∠B = 45° అయినది.
![]()
ఉదాహరణ -8:
7 సెం.మీ. పొడవుగల వృత్త జ్యా పై 60° కోణములను కలిగి ఉండే వృత్త ఖండాన్ని నిర్మించుము.
సాధన.
నిర్మాణ సోపానాలు:
సోపానం – 1: ఒక వృత్తాన్ని, 60° కలిగి ఉండే వృత్తఖండం యొక్క – (అధిక వృత్తఖండం గీయాలి. ఎందుకు ?) చిత్తు పటం గీయాలి. కేంద్రం లేకుండా వృత్తాన్ని గీయగలవా ?
విశ్లేషణ : ‘O’ కేంద్రంగా గల వృత్తం తీసుకోండి.
AB అనేది దత్త వృత్త జ్యా మరియు C = 60° కోణం గల ACB వృత్తఖండం మనం నిర్మించవలసినది.
AXB వృత్తచాపం వృత్తంపై C వద్ద చేసిన కోణం 60° అనుకోండి.
ACB = 60° కావున ∠AOB = 60° × 2 = 120° (ఎలా?)
∆DAB లో OA = OB (సమాన వ్యాసార్ధాలు) కావున
∴∠OAB = ∠OBA = \(\frac{180^{\circ}-120^{\circ}}{2}=\frac{60^{\circ}}{2}\) = 300
అందుచే మన ∆DAB గీయగలం. అప్పుడు వృత్తానికి OA = OB వ్యాసార్ధం అవుతుంది.
సోపానం – 2 :: AB = 7 సెం.మీ. రేఖాఖండం గీయండి.
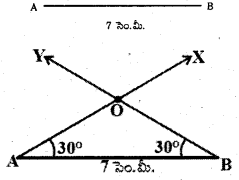
సోపానం – 3 : ∠BAX = 30° మరియు ∠YBA = 30° ఉండేటట్లు AX, BY కిరణాలను గీయగా అవి 0 వద్ద ఖండించుకుంటాయి. (సూచన : వృత్తలేఖిని ఉపయోగించి 60° కోణం నిర్మించి, దానిని సమద్విఖండన చేస్తే 30° కోణం వస్తుంది.)
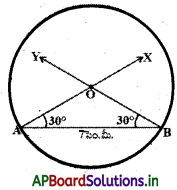
సోపానం – 4 : 0 కేంద్రంగా OA = OB = r వ్యాసార్ధంతో వృత్తం గీయాలి.
సోపానం – 5 : అధిక వృత్త చాపంపై ‘C’ బిందువు గుర్తించాలి. A, C మరియు B, C లను కలిపితే ∠ACB = 60° వస్తుంది.
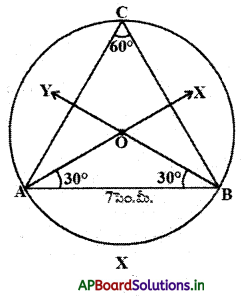
ఈ వృత్తఖండం మనకు కావలసిన వృత్తఖండం అవుతుంది. పై నిర్మాణాన్ని నిరూపిద్దాం . ఉపపత్తి : OA = OB (వృత్త వ్యాసార్థం)
∠OAB + ∠OBA = 30° + 30° = 60°
∴ ∠AOB = 180° – 60° = 120°
\(\widehat{\mathrm{AXB}}\)చాపం వృత్త కేంద్రం వద్ద చేయుకోణం 120°.
∴ ∠ACB = 120° = 60°
కావున ACB మనకు కావలసిన వృత్తఖండం అగును.