AP 9th Class Maths Notes 15th Lesson గణితములో నిరూపణలు

Students can go through AP Board 9th Class Maths Notes 15th Lesson గణితములో నిరూపణలు to understand and remember the concept easily.

AP Board 9th Class Maths Notes 15th Lesson గణితములో నిరూపణలు

→ ప్రవచనములను కొన్ని ప్రమాణములకు అనుగుణంగా నిర్ణయించబడును. సత్యం లేక అసత్య నిరూపణకు ఈ పద్ధతితో సంబంధంలేదు.

→ సాధారణ ప్రవచనములకంటే గణిత ప్రవచనములు కొంత వైవిధ్యత కలిగి ఉంటాయి. అవి సాక్ష్యాల ఆధారంతో ఋజువు – చేయలేము కాని ఒక ప్రత్యుదాహరణతో అసత్యమని చూపవచ్చు.

→ తార్కిక ఆలోచనలు, పరిశీలనలు, వరుస క్రమాల ఆధారంగా గణిత ప్రవచనమును ప్రవచించును. మన పరిశీలనలతో చేయు ఊహ పరికల్పనకు దారితీయును.

→ గణిత ప్రవచనము కొన్ని తార్కిక అంశముల ఆధారంగా సత్యమని ఋజువుచేసిన దానిని గణిత ప్రవచన నిరూపణ అంటారు.

→ నిరూపణ లేకుండానే సత్యములుగా భావించే గణిత ప్రవచనములను స్వీకృతములు అంటారు.

→ సత్యములుగా భావిస్తూ, ఇంతవరకూ నిరూపింపబడని గణిత ప్రవచనములను పరికల్పనలు (ఊహలు) అంటారు.

→ నిరూపింపబడిన గణిత ప్రవచనములను సిద్ధాంతములు అంటారు.

→ గణిత ప్రవచనములను తార్కిక ఆలోచనల ద్వారా నిరూపించుటను నిగమన పద్ధతి అంటారు.

→ నిరూపణ అనేది వరుస క్రమంలో వ్రాయబడిన గణిత ప్రవచనాల సమూహం.

→ సిద్ధాంతముల యందు ఇచ్చిన దత్తాంశము నుండి వరుసక్రమంలో తార్కిక వివేచన ద్వారా నిరూపించవలసిన విషయమును చేరుటయే సిద్ధాంత నిరూపణ అగును.

→ నిరూపించవలసిన అంశమునకు వ్యతిరేకముగా తీసుకొని, దత్తాంశమునకు విరుద్ధముగా నిరూపణ వచ్చినప్పుడు, అసలు నిరూపించవలసిన అంశమే సరియైనదని నిరూపించుట ద్వారా తెలుసుకొను విధానమును పరోక్ష పద్ధతి అంటారు.

→ అసందిగ్ధ ప్రవచనాల నుండి తార్కికంగా సత్యత నిర్ధారించుటయే నిగమన తార్కికత. వివిధ సందర్భాలలో సంగ్రహించిన సమాన క్రమము గల సామాన్యత మరియు అమరికలతో చేయు నిర్ణయమే అనుగమన – తార్కికత.

ఉదాహరణ – 1:
ప్రధాన సంఖ్యల నిర్వచనము నుండి 3 ఒక ప్రధాన సంఖ్య అని చెప్పగలము. కావున ఇది ఒక ప్రవచనము. మిగిభిన వాక్యములలో ప్రవచనములలో గణిత పరంగా నిరూపించగలిగేవి ఏవి ?
జవాబు :
ఈ ప్రవచన సత్య విలువ అసత్యము. కనుక ఒక ప్రత్యుదాహరణ ద్వారా మనము ఈ ప్రవచన సత్య విలువ నిర్ణయించగలము. ఒక ఉదాహరణ ద్వారా ఒక ప్రవచనం అసత్యము అని చెప్పవచ్చు. ఇటువంటి ఉదాహరణను ప్రత్యుదాహరణ అంటారు.

ఉదాహరణ – 2:
రెండు బేసి సంఖ్యల లబ్దము ఒక సరిసంఖ్య. ఏవైన రెండు బేసి సంఖ్యలు 9, 3 తీసుకొనుము. వాటి లబ్దము 3 × 5 = 15 ఇది సరిసంఖ్యకాదు.
జవాబు :
ఈ ప్రవచన సత్య విలువ అసత్యము. కనుక ఒక ప్రత్యుదాహరణ ద్వారా మనము ఈ ప్రవచన సత్య విలువ నిర్ణయించగలము. ఒక ఉదాహరణ ద్వారా ఒక ప్రవచనం అసత్యము అని చెప్పవచ్చు. ఇటువంటి ఉదాహరణను ప్రత్యుదాహరణ అంటారు.

ఉదాహరణ – 3:
క్రింది వాక్యములను పరిశీలించండి. “భూమిని పరిపాలించుటకు మనుష్యులు కలరు”, “రాము ఒక మంచి డ్రైవర్”.
జవాబు :
ఈ వాక్యములు సందిగ్ధదతో కూడి ఉన్న వాక్యములు. భూమిని పాలించుట అనునది కచ్చితముగా ఏ ప్రాంతము అనేది చెప్పబడలేదు. అదే విధముగా రెండవ వాక్యములో ఎటువంటి నైపుణ్యము మంచిదో అనేది స్పష్టంగా చెప్పబడలేదు. గణిత ప్రవచనములు కొన్ని పదాల కలయికతో, అందరికి స్పష్టంగా అర్థమగుతూ అది సత్యమో అసత్యమో నిర్ణయించగలిగేలా ఉండాలి.

ఉదాహరణ – 4:
భూమికి కల ఒకే ఒక ఉపగ్రహం చంద్రుడు. . లీలావతి అను గ్రంథమును భాస్కరుడు రచించెను. ఈ వాక్యములు ప్రవచనములు అవునో కాదో ఎట్లు నిర్ణయించగలవు ?
జవాబు :
ఈ వాక్యములలో సందిగ్ధత లేదు, కాని కొంత నిరూపించవలసిన అవసరము కలదు. దీనిని నిర్ధారించుటకు పూర్వము నిరూపించబడిన అంశములపై సంబంధించిన అంశములు తెలిసి ఉండాలి, రెండవ వాక్యము కొరకు పుస్తక రచయితలు వాటికి సంబంధించిన అంశములు చారిత్రక గ్రంథములు తెలియవలెను.

ఉదాహరణ – 5:
కింది ప్రవచనములు షరతులకు లోబడి సరియగు సత్య ప్రవచనములు అగునట్లుగా తిరిగి రాయండి.
(i) ప్రతి వాస్తవ సంఖ్య x కు 3x > x.
జవాబు :
x > 0 అయిన 3x > x.

(ii) ప్రతి వాస్తవ సంఖ్య x కు x ≥ 2x.
జవాబు :
x ≤ 50 లేదా x ≥ 21 అయిన x² ≥ 2x.

(iii) ఒక సంఖ్యను 2తో భాగించగా వచ్చిన సంఖ్య మొదటి సంఖ్యలో సగముండును.
జవాబు :
0 తప్ప మిగిలిన సంఖ్యలను 2 తో భాగిస్తే వచ్చు సంఖ్య మొదటి సంఖ్యలో సగముండును.

(iv) ఒక వృత్తములో ఒక జ్యా వృత్తముపై ఏదైన ఒక బిందువు వద్ద ఏర్పరచు కోణము 90°.
జవాబు :
ఒక వృత్తములో వృత్త వ్యాసము, వృత్తముపై ఏదైనా ఒక బిందువు వద్ద ఏర్పరచు కోణము 90°.

(v) ఒక చతుర్భుజంలో అన్ని భుజాలు సమానమైన అది ఒక చతురస్రము.
జవాబు :
ఒక చతుర్భుజంలోని అన్ని భుజాలు, కోణాలు సమానమైన అది ఒక చతురస్రము.

ఉదాహరణ – 6:
కింది వరుసల చుక్కలు ఒక వరుస క్రమ సంఖ్యలను సూచిస్తుంది.

a) తరువాతి మూడు పదాలు కనుక్కోండి.
b) 100వ పదము కనుక్కోండి.
c) nవ పదము కనుక్కోండి.

ఇచ్చట కల సంఖ్యలు T₁ = 2, T₂ = 6, T₃ = 12, T₄ = 20 గా కలదు. T₅, T₆, T_n పదములను ఊహించగలరా ? T_n అను పదమును ఒక భావనగా తీసుకుందాం.
పై విషయాన్ని తిరిగి ఇలా రాస్తే మనకు సాధనకు ఉపయోగపడవచ్చు.

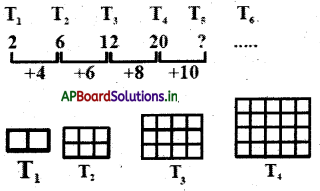
జవాబు :
కావున T₅ = T₄ + 10 = 20 + 10 = 30 = 5 × 6
T₆ = T₅ + 12 = 30 + 12 = 42
= 6 × 7 ……… T₇ ఊహించండి,
T₁₀₀ = 100 × 101 = 10, 100
T_n = n × (n + 1) = n² + n