Students can go through AP Board 9th Class Maths Notes 4th Lesson సరళ రేఖలు మరియు కోణములు to understand and remember the concept easily.
AP Board 9th Class Maths Notes 4th Lesson సరళ రేఖలు మరియు కోణములు
→ ఒక కిరణము అనేది సరళరేఖలోని భాగము. ఇది ఒక బిందువు వద్ద ప్రారంభమై నిర్దేశిత దిశలో అనంతంగా కొనసాగుతుంది.

→ సరళరేఖ రెండు వైపులా అనంతముగా పొడిగించబడుతుంది. ఈ

→ సాధారణంగా అన్ని సరళరేఖలను \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{PQ}}\) అని లేదా l, m, n వంటి అక్షరాలతో గానీ సూచిస్తారు. .10 ఒక సరళరేఖలో రెండు బిందువులు అంత్య బిందువులుగా కలిగిన భాగాన్ని రేఖాఖండము అంటారు.
![]()
\(\overline{\mathrm{PQ}}\) మరియు \(\overline{\mathrm{QR}}\) లు ఒకే రేఖాఖండాన్ని సూచిస్తాయి.
→ మూడు లేదా అంతకన్నా ఎక్కువ బిందువులు ఒకే సరళరేఖపై ఉంటే ఆ బిందువులను సరేఖీయ బిందువులని, కానిచో సరేఖీయాలు కాని బిందువులని అంటారు.

P, Q, R లను సరేఖీయాలని.
S, T లను సరేఖీయాలు కాని బిందువులని అంటారు.
→ ఒక వృత్తమును 360 సమాన భాగాలుగా చేయగా, ఒక్కొక్క భాగము కేంద్రము వద్ద చేయు కోణము ఒక డిగ్రీ అగును.
![]()
→ ఒక కిరణము, తొలి స్థానము నుండి తుది స్థానమునకు భ్రమణం చేయడం వలన కోణము ఏర్పడుతుంది.
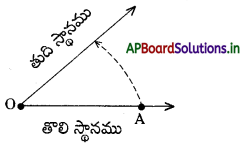
→ స్థిర బిందువు ఆధారముగా, ఒక కిరణము యొక్క తొలి స్థానము నుండి, తుది స్థానమునకు కలిగే మార్పును “భ్రమణము” అంటారు.
→ భగణపు కొలతను కోణమానినితో కొలవగా వచ్చిన విలువను “కోణము” అంటారు.
→ ఒక పూర్తి భ్రమణము విలువ 360°.
→ కోణమును ఏర్పరచు కిరణాలను కోణభుజాలు అని, వాటి ఉమ్మడి బిందువును కోణ శీర్షము అని అంటారు.
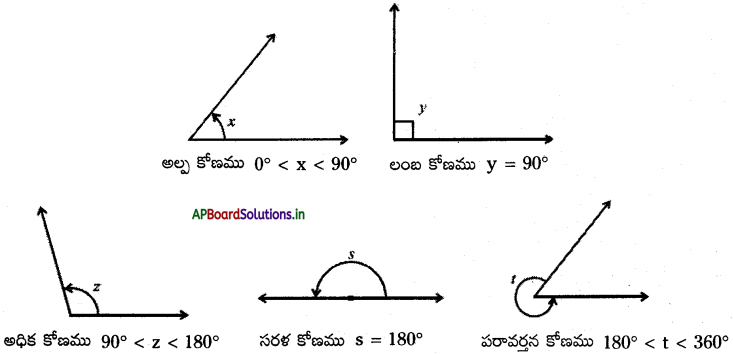
→ కోణాలలోని రకాలు : అల్ప కోణము, లంబ కోణము, అధిక కోణము, సరళ కోణము మరియు పరావర్తన కోణములు.
→ ఉమ్మడి బిందువులను కలిగి వుండని రేఖలను సమాంతర రేఖలు అంటారు.
ప్రక్క పటంలో l మరియు m లను సమాంతర రేఖలు అంటారు.

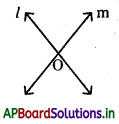
→ రెండు సరళరేఖలు ఏదైనా ఒక బిందువు వద్ద ఖండించుకుంటే వాటిని ఖండన రేఖలు అంటారు. ప్రక్క పటంలో l మరియు m లను ఖండన రేఖలు అంటారు.
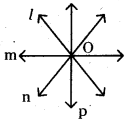
→ మూడు అంతకన్నా ఎక్కువ సరళరేఖలు ఒకే బిందువు వద్ద ఖండించుకుంటే ఆ సరళరేఖలను మిళితరేఖలు అని, ఆ బిందువును మిళిత బిందువు అని అంటారు. l, m, n మరియు p లను మిళిత రేఖలని, ‘O’ ను మిళిత బిందువు అని అంటారు.
→ ఏవైనా రెండు కోణాల మొత్తము 180° కు సమానమైన, ఆ కోణాలను “సంపూరక కోణములు” అంటారు. ‘
ఉదా : (100°, 80°), (110°, 70°), (120°, 60°), (104°, 76°), (179°, 1°) మొ||నవి.
→ ఏవైనా రెండు కోణముల మొత్తము 90° కు సమానమైన, ఆ కోణాలను “పూరక కోణములు” అంటారు.
ఉదా : (89°, 1°), (70°, 20°), (60°, 30°) మొ||నవి.
→ ఇచ్చిన కోణము x° అయిన దాని యొక్క పూరక కోణము విలువ (90° – x°).
→ ఇచ్చిన కోణము x° అయిన దాని యొక్క సంపూరక కోణము విలువ (180° – x°).
![]()
→ ఏవైనా రెండు కోణముల మొత్తము 360° కు సమానమైన, ఆ కోణములను “సంయుగ్మ కోణములు” అంటారు.
ఉదా : (120°, 240°), (100°, 260°), (180°, 180°), (50°, 31°) మొ॥నవి.
→ ఉమ్మడి శీర్షము, ఉమ్మడి భుజం కలిగి, ఉమ్మడి భుజమునకు చెరొక వైపున ఉన్న కోణాల జతను ఆసన్న కోణాల జత అంటాము.
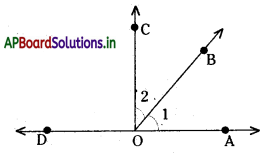
పై పటంలో \(\overline{\mathrm{OB}}\) ఉమ్మడి భుజము, ∠1, ∠2 లు ఆసన్న కోణాలు.
→ ఏవైనా రెండు ఆసన్న కోణాల మొత్తము 180° అయిన ఆ కోణాలను “రేఖీయ ద్వయం” అంటాము. .
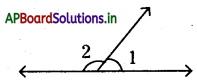
పై పటం నుండి ∠1 + ∠2 = 180° అయిన ∠1 మరియు ∠2 లను రేఖీయ ద్వయం అంటారు.
→ రెండు సరళరేఖలు ఖండించుకొనగా ఒకే శీర్షాన్ని కల్గి వుండి ఉమ్మడి భుజములేని అభిముఖ కోణాలను, శీర్షాభిముఖ కోణాలు అంటారు.
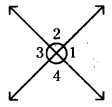
పై పటంలో (∠1, ∠3) లు మరియు (∠2, ∠4) లు శీర్షాభిముఖ కోణాలు.
→ రెండు సళరరేఖలు ఖండించుకొనగా ఏర్పడిన శీర్షాభిముఖ కోణములు సమానము. ప్రక్కపటంలో a = c మరియు b = d అగును.

→ రెండు సరళరేఖలను, ఒక తిర్యగ్రేఖ ఖండించగా మొత్తము ‘8’ కోణములు ఏర్పడును.
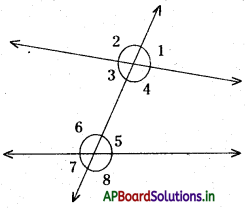
ప్రక్కపటంలో బాహ్యకోణములు ∠1, ∠2, ∠7 మరియు ∠8
అంతరకోణములు ∠3, ∠4, ∠5 మరియు ∠6
→ ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించగా ఏర్పడు ప్రతి సదృశ్య కోణాల జత, ప్రతి ఏకోంతర కోణాల జత మరియు ప్రతి ఏకాంతర బాహ్య కోణాల జతలు సమానము.
→ రెండు సమాంతర రేఖలను, ఒక తిర్యగ్రేఖ ఖండించగా ఏర్పడు ఒకే వైపునున్న ప్రతీ అంతరకోణాల జత సంపూరకాలు.
→ రెండు సరళరేఖలు సమాంతరాలని చూపుటకు క్రింది నియమాలు పాటించవలెను.
- సదశ్యకోణాల జత సమానమని చూపవలెను.
- ఏకాంతర కోణాల జత సమానమని చూపవలెను.
- తిర్యగ్రేఖకు ఒకే వైపునున్న అంతరకోణాలు సంపూరకాలని చూపవలెను.
- ఒక తలంలో ఇచ్చిన రెండు సరళరేఖలు, మూడవ రేఖకు లంబమని చూపవలెను.
- ఇచ్చిన రెండు సరళరేఖలను, మూడవ రేఖకు సమాంతరరేఖలని చూపవలెను.
→ త్రిభుజంలోని అంతరకోణాల మొత్తము 180.
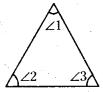
ప్రక్కపటంలో,
∠1 + ∠2 + ∠3 = 180°
![]()
→ ఒక త్రిభుజ భుజాన్ని పొడిగించగా ఏర్పడిన బాహ్యకోణం, ఆ త్రిభుజ అంతరాభిముఖ కోణాల మొత్తంకు,సమానము.
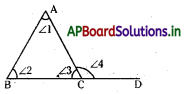
ప్రక్కపటంలో, ∠1 + ∠2 = ∠4 అగును.