Students can go through AP Board 9th Class Maths Notes 3rd Lesson జ్యామితీయ మూలాలు to understand and remember the concept easily.
AP Board 9th Class Maths Notes 3rd Lesson జ్యామితీయ మూలాలు
→ మన దైనందిన కార్యక్రమములైన చిత్రలేఖనం, హస్తకళలు, గదుల నేలమీద రాళ్లను పర్చడం, పొలాలను దున్నడం, విత్తనాలను నాటడం వంటి వాటిలో జ్యామితి సూత్రాలను ఉపయోగిస్తాము.
→ జ్యామితి అనువర్తనాలకు కొన్ని ఉదాహరణలు ఈజిప్టులోని పిరమిడ్లు, చైనా కుడ్యము, భారతదేశపు ఆలయాలు మరియు యజ్ఞ వాటికలు, ఫ్రాన్స్ లోని ఈఫిల్ టవర్ వంటి ప్రసిద్ధ కట్టడాలు మొదలగునవి.
→ అనిర్వచిత పదాలైన “బిందువు”, “రేఖ” మరియు “తలము” అనునవి జ్యా మితి యొక్క పునాది రాళ్లుగా చెప్తాము.
→ బిందువు, రేఖ మరియు తలం వంటి అనిర్వచిత పదాలను యూక్లిడ్ తో సహ అనేకమంది .గణిత శాస్త్రవేత్తలు నిర్వచించడానికి ప్రయత్నించారు.
→ యూక్లిడ్ తన “ఎలిమెంట్స్” అను సంకలనంలో ఒక నూతన ఆలోచనా విధానాన్ని అభివృద్ధి చేసాడు. ఈ వ్యవస్థ తర్వాతి గణిత అభివృద్ధికి పునాదిగా నిలిచింది.
→ యూక్లిడ్ సామాన్య భావనలలో కొన్ని
- ఒకే రాశులకు సమానమైన రాశులు సమానం.
- సమాన రాశులను, సమాన రాశులకు కూడినచో వచ్చు మొత్తాలు సమానము.
- సమాన రాశులను, సమాన రాశుల నుండి తీసివేసినచో వాటి భేదాలు సమానము.
- ఒక దానితో మరొకటి ఏకీభవించే పటాలు సమానాలు.
- ఒక వస్తువు దాని భాగము కంటే పెద్దది.
- సమాన రాశుల రెట్టింపులు సమానాలు.
- సమాన రాశులలో సగాలు సమానం.
![]()
→ యూక్లిడ్ జ్యామితీయ స్వీకృతాలు :
- స్వీకృతం – 1 : ఒక బిందువు నుండి ఏ బిందువుకైనను రేఖను గీయవచ్చును.
(లేదా)
రెండు వేర్వేరు బిందువుల గుండాపోయే సరళరేఖ ఏకైకంగా వుంటుంది. - స్వీకృతం – 2 : ఒక రేఖాఖండాన్ని ఇరువైపులా అనంతముగా పొడిగించవచ్చును.
- స్వీకృతం – 3. : ఇచ్చిన కేంద్రం మరియు వ్యాసార్ధాలతో వృత్తమును గీయవచ్చును.
- స్వీకృతం – 4 : లంబకోణాలన్నీ ఒకదానితో మరొకటి సమానము.
- స్వీకృతం – 5 : రెండు దత్త సరళరేఖలను ఖండించు సరళరేఖ దానికి ఒకేవైపున ఉన్న అంతరకోణాల మొత్తం రెండు లంబకోణాల కన్నా తక్కువగా ఉండునట్లు చేస్తే అప్పుడు దత్త సరళరేఖలను నిరంతరం 2. పొడిగిస్తే అవి రెండు లంబకోణాల కన్నా తక్కువైన మొత్తం గల. కోణాల వైపున కలుసుకొంటాయి.
→ కొందరు గణిత శాస్త్రవేత్తలు ‘5’వ స్వీకృతానికి సమానార్థ (లేదా) తుల్య ప్రవచనాలను ప్రతిపాదించారు.
![]()
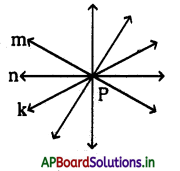
→ ప్లేఫెయిర్ స్వీకృతము : ఒక సరళరేఖకు దానిపై లేనటువంటి ఏదేని బిందువు గుండా ఒకే ఒక సమాంతర రేఖను గీయవచ్చు. ‘l’ అనునది ఒక సరళరేఖ మరియు ‘P’ అనునది ‘l’ పై లేనట్టి ఏదేని ఒక బిందువు. అయిన ‘l’ కు. . సమాంతరంగా ‘P’ ద్వారా పోయే ఒకే ఒక సరళరేఖ వ్యవస్థితమవుతుంది.
→ లెజెండర్ స్వీకృతం : ఒక త్రిభుజం యొక్క కోణాల మొత్తం ఎల్లప్పుడూ ‘ స్థిరంగా వుంటుంది మరియు ఇది రెండు లంబకోణాలకు సమానము.
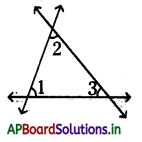
∴ ∠1 + ∠2 + ∠3 = 180°
→ పొసిడోమినస్ స్వీకృతం : రెండు రేఖలు వాటి మధ్య దూరం సమానంగా ఉండునట్లు అంతటా వ్యవస్థితమవుతాయి.
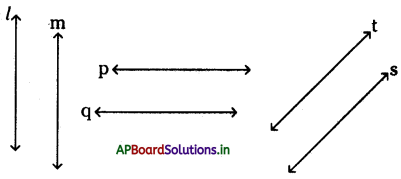
→ ప్రోక్లస్ స్వీకృతం : ఒక జత సమాంతర రేఖలలో ఒకదానిని ఏదేని సరళరేఖ ఖండించిన, అది సమాంతర రేఖలలో రెండవ దానిని కూడా ఖండిస్తుంది.
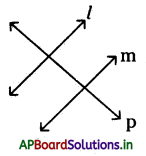
→ రెండు రేఖలు ఒకే రేఖకు సమాంతరమైన అవి ఒకదానికి మరొకటి సమాంతరంగా వుంటాయి.
→ గోల్డ్ బ్యాక్ పరికల్పన : నాలుగు లేక అంతకన్నా పెద్దదైన ప్రతి సరిసంఖ్యను కూడా రెండు ప్రధాన సంఖ్యల మొత్తంగా
రాయవచ్చును.
![]()
→ సత్యమని నిరూపించబడిన పరికల్పనలన్నీ సిద్ధాంతాలుగా రూపొందుతాయి.
→ ఒక సిద్ధాంతాన్ని తార్కిక సోపానాల క్రమంతో నిరూపిస్తాము.
→ “సిద్దాంత నిరూపణ” అనునది సిద్ధాంతం’ యొక్క సత్య విలువను సందేహానికి తావులేకుండా నిరూపించే ఒక “తార్కికవాద ప్రక్రియ”.
→ యూక్లిడ్ జ్యామితిలోని ఐదవ స్వీకృతంనకు బదులుగా వేరే స్వీకృతాలను ప్రతిక్షేపిస్తే వాటిని యూక్లిడేతర జ్యామితులు అంటారు.