AP 9th Class Maths Notes 5th Lesson నిరూపక జ్యామితి

Students can go through AP Board 9th Class Maths Notes 5th Lesson నిరూపక జ్యామితి to understand and remember the concept easily.

AP Board 9th Class Maths Notes 5th Lesson నిరూపక జ్యామితి

→ ఒక బిందువు యొక్క స్థానాన్ని గుర్తించుటకు మనకు రెండు నిర్దేశాలు అవసరము.

→ ఒక తలంలో ఏదైనా బిందువును రెండు నిర్దేశాల ఆధారంగా స్థాపించవచ్చును.

→ వైశ్లేషిక రేఖాగణితంను “రేన్ డెకార్టె” అను గణిత శాస్త్రజ్ఞుడు అభివృద్ధిపరిచాడు.

→ రేన్ డెకార్టి బీజీయ సమీకరణాలకు మరియు రేఖాగణిత వక్రాలకు, పటాలకు మధ్య సంబంధాన్ని కనుగొన్నాడు.

→ వైశ్లేషిక రేఖాగణితాన్ని, నిరూపక రేఖాగణితం అని కూడా అంటారు.

→ పరస్పరం లంబంగా వుండే రెండు సంఖ్యారేఖల ఆధారంగా మనము ఒక తలంలో ఏదైనా బిందువు లేదా వస్తువు స్థానాన్ని నిర్ధారించవచ్చును.

→ లంబంగా వుండే రేఖలలో, ఒక రేఖను శిక్షితిజ సమాంతరంగా మరొక రేఖను క్షితిజ లంబంగా గీచిన అవి ఒక బిందువు వద్ద పరస్పరం ఖండించుకుంటాయి. ఈ ఖండన బిందువునే “మూల బిందువు” అంటారు.

→ క్షితిజ సమాంతర రేఖ XX’ ను X – అక్షం అనీ, క్షితిజ లంబరేఖ YY’ ను Y – అక్షం అని అంటారు.

→ ప్రక్క పటంలో
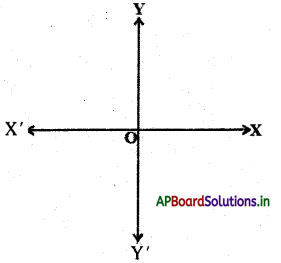
AP 9th Class Maths Notes 5th Lesson నిరూపక జ్యామితి 1

\(\overrightarrow{\mathrm{OX}}\) ను ధన X – అక్షం అని అంటారు.
\(\overrightarrow{\mathrm{OY}}\) ను ధన Y – అక్షం అని అంటారు.
\(\overline{\mathrm{OX}}^{\prime}\) ను ఋణ X – అక్షం అని అంటారు.
\(\overline{\mathrm{OY}}^{\prime}\) ను ఋణ Y – అక్షం అని అంటారు.

→ ప్రక్క పటంలోని తలం వరుసగా అపసవ్య దిశలో Q₁, Q₂, Q₃, మరియు Q₄ భాగాలుగా విభజించబడినది. ఈ భాగాలను వరుసగా మొదటి పాదం (Q₁), రెండవ పాదం (Q₂), మూడవ పాదం (Q₃), నాల్గవ పాదం (Q₄) అని పిలుస్తారు.
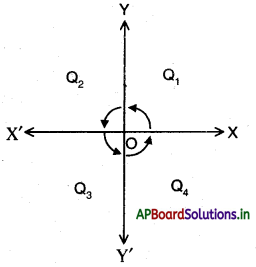
AP 9th Class Maths Notes 5th Lesson నిరూపక జ్యామితి 2

→ ఈ రకమైన తలాన్ని కార్టిజియన్ తలం లేదా నిరూపక తలం లేదా XY-తలం అని అంటారు. అదే విధంగా X, Y అక్షాలను – నిరూపకాక్షాలు అని అంటారు.

→ ఒక నిరూపక తలంలో X-అక్షం నుండి ఒక బిందువుకు గల దూరాన్ని Y-నిరూపకమని, Y-అక్షం నుండి అదే బిందువుకు గల దూరాన్ని X – నిరూపకమని అంటారు.

→ x- నిరూపకాన్ని ప్రథమ నిరూపకం అని, y – నిరూపకాన్ని ద్వితీయ నిరూపకం అని అంటారు.

→ ఒక తలంలోని ఏ బిందువు నిరూపకాలైనా ఏకైకంగా ఉంటాయి.

→ మూల బిందువు నిరూపకాలు (0, 0).

→ బిందు నిరూపకాల గుర్తులకు మరియు నిరూపక తలంలో ఆ బిందువు ఉండే పాదాలకు మధ్య సంబంధము :
AP 9th Class Maths Notes 5th Lesson నిరూపక జ్యామితి 3

→ నిరూపకాల ఆధారంగా కార్టిజియన్ తలంలో ఒక బిందువును స్థాపించడాన్ని “బిందు స్థాపన” అని అంటారు.

→ (x, y) క్రమయుగ్మము (y, x) క్రమయుగ్మము ఒకటికాదు.

→ X – అక్షం యొక్క సమీకరణం y = 0.

→ Y- అక్షం యొక్క సమీకరణం x = 0.

→ ఒక నిరూఫక తలంలో (x₁, y₁) ≠ (x₂, y₂), x₁ = x₂ మరియు y₁ = y₂ అయితే తప్ప.

→ Y – అక్షంపై X – నిరూపకము సున్న.

→ X – అక్షంపై y – నిరూపకము సున్న.