AP Board 10th Class Maths Solutions Chapter 5 వర్గ సమీకరణాలు Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 5 వర్గ సమీకరణాలు Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 5th Lesson వర్గ సమీకరణాలు Optional Exercise

ప్రశ్న 1.
ఒక తలంలో కొన్ని బిందువులు గుర్తించబడినవి. ప్రతి బిందువు మిగిలిన అన్ని బిందువులతో రేఖండాలచే కలుపబడింది. ఈ విధంగా చేయటం వల్ల మొత్తం 10 రేఖాఖండాలు ఏర్పడితే మొత్తం బిందువులు ఎన్ని ? (గమనిక: సమస్యలో ఏ మూడు బిందువులు సరేఖీయాలు కాని కొన్ని బిందువులు గుర్తించబడ్డాయి. అని ఇవ్వాలి.)
సాధన.
ఏ మూడు బిందువులు సరేఖీయాలు కాని n బిందువులలో ప్రతి బిందువును మిగిలిన అన్ని బిందువులతో కలుపగా ఏర్పడే రేఖాఖండాల సంఖ్య = \(\frac{1}{2}\) n(n – 1)
కాని లెక్క ప్రకారం రేఖా ఖండాల సంఖ్య = 10

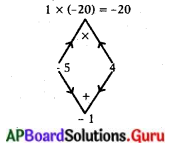
\(\frac{1}{2}\) n(n – 1) = 10
n(n – 1) = 20
n² – n – 20 = 0
n² – 5n + 4n – 20 = 0
n(n – 5) + 4(n – 5) = 0
(n – 5) (n + 4) = 0
n – 5 = 0 లేదా n + 4 = 0
n = 5 లేదా n = – 4
బిందువుల సంఖ్య రుణాత్మకం కాదు కావున n = 5
∴ బిందువుల సంఖ్య n = 5
సరిచూచుట :

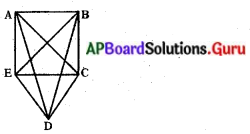
A, B, C, D, E లు ఏ మూడు సరేఖీయాలు కొని 5 బిందువులు వీటితో ఏర్పడే రేఖాఖండాలు AB, BC, CD, DE, EA, AC, AD, BE, BD, CE మొత్తం 10 రేఖాఖండాలు కలవు.

ప్రశ్న 2.
ఒక రెండంకెల సంఖ్యలో అంకెల లబ్ధం &. ఈ సంఖ్యకు – . 18 కలిపిన వచ్చే సంఖ్య మొదటి సంఖ్యలోని అంకెలను తారుమారు చేయగా వచ్చే సంఖ్య ఒక్కటే. అయిన మొదటి సంఖ్యను కనుగొనుము.
సాధన.
ఒకట్ల స్థానంలోని అంకె = x
పదుల స్థానంలోని అంకె = y అనుకొందాం.

లెక్క ప్రకారం అంకెల లబ్ధం = 8
∴ xy = 8
⇒ y = \(\frac{8}{x}\) ………… (1)
మరియు సంఖ్యకు 18 కలిపిన వచ్చే సంఖ్య = ఆ సంఖ్యలోని అంకెలను తారుమారు చేయగా వచ్చే సంఖ్య
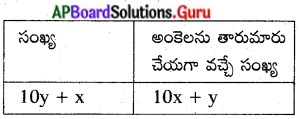
(10y + x) + 18 = 10x + y
10y + x + 18 – 10x – y = 0
9y – 9x + 18 = 0
9(y – x + 2) = 0
∴ y – x + 2 = 0 లో (1)ని ప్రతిక్షేపించగా

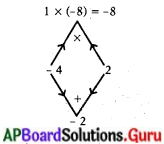
\(\frac{8}{x}\) – x + 2 = 0

\(\frac{8-x^{2}+2 x}{x}\) = 0
8 – x² + 2x = 0
⇒ x² – 2x – 8 = 0
x² – 4x + 2x – 8 = 0
x(x – 4) + 2 (x – 4) = 0
(x – 4) (x + 2) = 0
x – 4 = 0
x = 4
x + 2 = 0
x = – 2
సంఖ్యలోని అంకె రుణాత్మకం కాదు. ఒకట్ల స్థానం x = 4 –
పదుల స్థానం y = \(\frac{8}{4}\) = 2 (∵ (1) నుండి)
∴ కావలసిన సంఖ్య = 24.

సరిచూచుట :
24 + 18 = 42 .

ప్రశ్న 3.
8 మీ. పొడవు వున్న తీగను రెండు ముక్కలుగా కత్తిరించారు. ప్రతి ముక్కను తిరిగి ఒక చతురస్రాకారంగా వంచారు. ఇలా ఏర్పడిన రెండు చతురస్రాల వైశాల్యాల మొత్తం 2 చ.మీ. కావలెనన్న ప్రతి ముక్క పొడవు ఎంత వుండాలి ?
[x + y = 8, \(\left(\frac{x}{4}\right)^{2}+\left(\frac{y}{4}\right)^{2}\) = 2
⇒ \(\left(\frac{x}{4}\right)^{2}+\left(\frac{8-x}{4}\right)^{2}\) = 2]
సాధన.

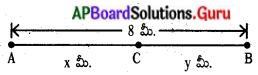
మొదటి ముక్క పొడవు = x మీ.
రెండవ ముక్క పొడవు = y మీ. అనుకొనుము.
x + y = 8
y = 8 – x ……… (1)
ప్రతి ముక్కను ఒక చతురస్రంగా వంచిన మొదటి ముక్క యొక్క చతురస్ర చుట్టుకొలత = x మీ
భుజము = \(\frac{x}{4}\) మీ.
వైశాల్యం = (\(\frac{x}{4}\))² చ.మీ.
రెండవ ముక్క యొక్క చతురస్ర చుట్టుకొలత = y మీ.
భుజము = \(\frac{y}{4}\) మీ.
వైశాల్యం = (\(\frac{x}{4}\))² = \(\frac{(8-x)^{2}}{4}\) (∵ (1) నుండి)
కాని లెక్క ప్రకారం వైశాల్యం మొత్తం = 2 చ.మీ.
\(\left(\frac{x}{4}\right)^{2}+\left(\frac{8-x}{4}\right)^{2}\) = 2

\(\frac{x^{2}}{16}+\frac{(8-x)^{2}}{16}\) = 2

\(\frac{x^{2}+64-16 x+x^{2}}{16}\) = 2
2x² – 16x + 64 = 32
2x² – 16x + 64 – 32 = 0
2x² – 16x + 32 = 0
2(x² – 8x + 16) = 0
x² – 8x + 16 = 0
x² – 2. x . 4 + 4² = 0.
(x – 4)² = 0
ఈ సందర్భంలో మూలాలు సమానము.
x – 4 = 0
x = 4
∴ మొదటి ముక్క పొడవు x = 4 మీ.
రెండవ ముక్క పొడవు y = 8 – 4 = 4 మీ. [∵ (1) నుండి]

సరిచూచుట :
చతురస్ర భుజాలు 1 మీ. మరియు 1 మీ. వైశాల్యా ల మొత్తం 1² + 1² = 1 + 1 = 2 చ.మీ.

ప్రశ్న 4.
వినయ్ మరియు ప్రవీళ్లు కలసి ఒక ఇంటికి రంగులు వేసే పనిని 6 రోజులలో పూర్తి చేయగలరు. వినయ్ ఒక్కడే ఆ పనిని ప్రవీణ్ కంటే 5 రోజులు ముందుగా పూర్తి చేయగలడు. అయిన వినయ్ ఒక్కడే ఆ పనిని ఎన్ని రోజులలో పూర్తి చేయగలడు ?
సాధన.
ప్రవీణ్ ఒక్కడే ఆ పనిని పూర్తి చేయుటకు పట్టే కాలం = x రోజులు అనుకొనుము.
వినయ్ ఒక్కడే ఆ పనిని పూర్తి చేయుటకు పట్టే కాలం = (x – 5) రోజులు.
ప్రవీణ్ ఒక్కడే ఒక రోజులో చేసే పని = \(\frac{1}{x-5}\)
వినయ్ ఒక్కడే ఒక రోజులో చేసే పని = \(\frac{1}{6}\)
లెక్క ప్రకారం ప్రవీణ్ మరియు వినయ్ లు కలసి ఒక రోజులో చేసే పని = \(\frac{1}{6}\)
\(\frac{1}{x}+\frac{1}{x-5}=\frac{1}{6}\)

\(\frac{(x-5)+x}{x(x-5)}=\frac{1}{6}\) \(\frac{2 x-5}{x^{2}-5 x}=\frac{1}{6}\)

∴ x² – 5x = 6(2x – 5)
x² – 5x = 12x – 30
x² – 5x – 12x + 30 = 0
x² – 17x + 30 = 0

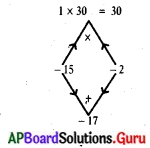
x² – 15x – 2x + 30 = 0
x(x – 15) – 2(x – 15) = 0
(x – 15) (x – 2) = 0.
x – 15 = 0 లేదా x – 2 = 0
x = 15 లేదా x = 2
x = 15 అయిన x – 5 = 10
x = 2 ⇒ x – 5 = – 3
రోజుల సంఖ్య ఋణాత్మకం కాదు. కావున x ≠ 2.
వినయ్ ఒక్కడే ఆ పనిని పూర్తి చేయుటకు పట్టే కాలం x – 5 = 10 రోజులు

సరిచూచుట :
వినయ్ మరియు ప్రవీలు కలసి ఒక రోజులో చేసే పని = \(\frac{1}{10}+\frac{1}{15}=\frac{3+2}{30}=\frac{5}{30}=\frac{1}{6}\)
∴ ఇద్దరూ కలసి ఆ పనిని 6 రోజులలో పూర్తి చేస్తారు.

ప్రశ్న 5.
ఒక వర్గ సమీకరణం యొక్క మూలాలు మొత్తం : అని చూపుము.
సాధన.
ax² + bx + c = 0 వర్గ సమీకరణం యొక్క మూలాలు α, β అనుకొందాం.
వర్గ సూత్రం నుంచి
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
మూలాలు α = \(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\) మరియు β = \(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\)

మూలాల మొత్తం

మూలాల మొత్తం α + β = \(-\frac{b}{a}\)
∴ ax² + bx + c = 0 వర్గ సమీకరణ మూలాల మొత్తం = \(-\frac{b}{a}\).

ప్రశ్న 6.
ఒక వర్గ సమీకరణం యొక్క మూల చూపుము.
సాధన.
వర్గ సమీకరణం ax² + bx + c = 0 మూలాలు
α = \(\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\) మరియు β = \(\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\)
మూలాల లబ్దం

మూలాల లబ్ధం αβ = \(\frac{c}{a}\)
∴ ax² + bx + c = 0 వర్గ సమీకరణ మూలాల లబ్ధం = \(\frac{c}{a}\)

ప్రశ్న 7.
ఒక భిన్నములో హారము, లవము యొక్క రెట్టింపు కంటే ఒకటి ఎక్కువ. ఆ భిన్నము మరియు దాని వుత్రమాల మొత్తము 2\(\frac{16}{21}\) అయిన ఆ భిన్నమును కనుగొనుము.
సాధన.
లవము = x అనుకొనిన
హారము = 2x + 1 (∵ హారము, లవము యొక్క రెట్టింపు కంటే ఒకటి ఎక్కువ)
భిన్నము = \(\frac{x}{2 x+1}\)
భిన్నము యొక్క వ్యుత్తమము = \(\frac{2 x+1}{x}\)
లెక్క ప్రకారం భిన్నము మరియు దాని వ్యుత్ర్కమాల మొత్తం = 2\(\frac{16}{21}\) = \(\frac{58}{21}\)

\(\frac{x}{2 x+1}+\frac{2 x+1}{x}=\frac{58}{21}\) \(\frac{x^{2}+(2 x+1)^{2}}{(2 x+1) x}=\frac{58}{21}\) \(\frac{x^{2}+4 x^{2}+4 x+1}{2 x^{2}+x}=\frac{58}{21}\)

58 (2x² + x) = 21 (5x² + 4x + 1) (అడ్డగుణకారం చేయగా)
116x² + 58 x = 105x² + 84x + 21
116x² + 58 x – 105x² – 84x – 21 = 0
11x² – 26x – 21 = 0 …………… (1)
a = 11, b = – 26, c = -21
b² – 4ac = (- 26)² – 4 (11) (- 21)
= 676 + 924 = 1600
∴ వర్గ సూత్రం x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

x = \(\frac{-(-26) \pm \sqrt{1600}}{2(11)}=\frac{26 \pm 40}{22}\)

x = \(\frac{26+40}{22}=\frac{66}{22}=3\) లేదా

x = \(\frac{26-40}{22}=\frac{-14}{22}=\frac{-7}{11}\)
భిన్నం యొక్క లవ, హారాలు పూర్ణ సంఖ్యలు. కావున
∴ x = 3.
లవము x = 3
హారము 2x + 1 = 7
కావలసిన భిన్నము = \(\frac{3}{7}\)

సరిచూచుట :
భిన్నము. + వ్యుత్రమం = \(\frac{3}{7}+\frac{7}{3}=\frac{9+49}{21}=\frac{58}{21}=2 \frac{16}{21}\)

(లేదా)

(1) ⇒ 11x² – 26x – 21 = 0

11x² – 33x + 7x – 21 = 0
11x (x – 3) + 7 (x – 3) = 0
(x – 3) (11x + 7) = 0
11 x (- 21) = – 231

3 × 7 × 11 = 231
x – 3 = 0
x = 3
11x + 7 = 0
11x = – 7
x = \(\frac{-7}{11}\)
భిన్నం యొక్క లవ, హారాలు మళ్ళీ భిన్నాలు కాదు. కావున
x = 3
లవము x = 3
హారము 2x + 1 =7
∴ కావలసిన భిన్నము = \(\frac{3}{7}\)

ప్రశ్న 8.
29.4 మీ. ఎత్తుగల భవనం పైభాగం నుంచి 24.5 మీ/ – సేక. శాలి వేగుతో ఒక బంతి పైవైపుకు విసిరి వేయబడింది. ‘1 సెకనుల తరువాత భూమట్టం నుండి బంతి యొక్క ఎత్తు H = 29.4 + 24.5 t – 4.9 t² అయితే ఆ బంతి భూమిని ఎన్ని సెకనుల తరువాత . తాకుతుంది ?
సాధన.

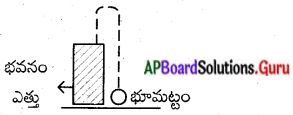
తొలివేగం ‘U’ = 24.5
భూమట్టం నుండి బంతి యొక్క ఎత్తు H = 29.4 + 24.5 t- 4.9 t²
బంతి భూమట్టాన్ని, ‘t’ సెకనులలో చేరింది. అనగా భూమట్టం నుండి ఎత్తు H = 0
కనుక 29.4 + 24.5t – 4.9t² = 0 = H
⇒ 4.9 t² – 24.5t – 29.4 = 0
⇒ 4.9 [t² – 5t – 6] = 0
∴ t² – 5t – 6 = 0
⇒ t² – 6t + 1 – 6 = 0
⇒ t(t – 6) + 1(t – 6) = 0
(t- 6) (t + 1) = 0
⇒ t – 6 = 0
∴ t = 6
లేదా t + 1 = 0 ⇒ t = – 1 కాని ‘t’ ఋణాత్మకం కాదు.
కనుక t = 6
∴ బంతి భూమిని తాకిన కాలము = t = 6 సెకనులు.