AP Board 10th Class Maths Solutions Chapter 6 శ్రేఢులు Exercise 6.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 6 శ్రేఢులు Exercise 6.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 6th Lesson శ్రేఢులు Exercise 6.1

ప్రశ్న 1.
ఈ క్రింది సంఘటనలలో ఏ సంఘటనలో ఏర్పడే సంఖ్యల జాబితా అంకశ్రేఢి అవుతుంది ? ఎందుకు ?
(i) ఒక టాక్సీకి మొదటి గంట ప్రయాణానికి ₹ 20 చొప్పున తరువాత ప్రతి గంటకు ₹ 8 చొప్పున చెల్లించవలసి ఉన్న ప్రతి కిలోమీటరుకు చెల్లించవలసిన సొమ్ము.
(ఇచ్చిన సమస్య స్పష్టంగా లేదు. టాక్సీ అద్దె గంటలకు ఇవ్వబడినది. కాని చెల్లించాల్సిన సొమ్మును కిలో మీటరుకు ఇవ్వడం జరిగినది).
సరైన సమస్య : ఒక టాక్సీ మొదటి కిలోమీటరు ప్రయాణానికి ₹ 20 లు చొప్పున తరువాత ప్రతి కిలోమీటరుకు ₹8 లు చొప్పున చెల్లించవలసి వున్న ప్రతి కిలోమీటరుకు చెల్లించవలసిన సొమ్ము.
సాధన.

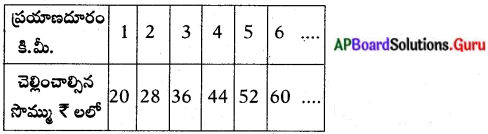
సంఖ్యల జాబితా : 20, 28, 36, 44, 52, 60

సామాన్యభేదము

ప్రతి సందర్భంలోను సామాన్యభేదం సమానము. కావున ఏర్పడే సంఖ్యల జాబితా ఒక అంకశ్రేణి (A.P.) అవుతుంది.

(ii) ఒక వాక్యూమ్ పంపు సిలిండరులో ఉండే గాలి నుంచి 1/4 వంతు తీసివేయును. అయిన ప్రతిసారీ సిలెండరులో మిగిలి వుండే గాలి పరిమాణము.
సాధన.
సిలెండరులో గల గాలి పరిమాణము = 1 అనుకొందాం.

సంఖ్యల జాబితా 1, \(\frac{3}{4}\), \(\frac{9}{16}\), \(\frac{27}{64}\), …………..

సామాన్యభేదం d = a₂ – a₁ = \(\frac{3}{4}\) – 1
= \(\frac{3-4}{4}=-\frac{1}{4}\)

= a₃ – a₂ = \(\frac{9}{16}\) – \(\frac{3}{4}\)
= \(\frac{9-12}{16}=\frac{-3}{16}\)
అన్ని సందర్భాలలో సామాన్యభేదం సమానంగా లేదు. కావున ఈ జాబితా అంకశ్రేణి కాదు.

(iii) ఒక బావిని తవ్వడానికి మొదట మీటరుకు ₹ 150 వంతున ఆపై ప్రతి మీటరుకు ₹ 50 వంతున చెల్లించాలి. అయిన ప్రతి మీటరుకు చెల్లించవలసిన సొమ్ము.
సాధన.

సంఖ్యల జాబితా 150, 200, 250, 300, 350,

సామాన్యభేదం

అన్ని సందర్భాలలోను సామాన్య భేదం సమానము. కావున ఈ సంఖ్యల జాబితా అంకశ్రేఢి (A.P.) అవుతుంది.

(iv) ఒక బ్యాంకులో ₹ 10000 లను సంవత్సరానికి 8 శాతం చక్రవడ్డీ ప్రకారం పొదుపు చేసిన ప్రతి సంవత్సరము చివరలో ఖాతాలో ఉండే సొమ్ము.
సాధన.
ప్రారంభంలో ఖాతాలో గల సొమ్ము (P) = ₹10,000 వడ్డీరేటు (R) = 8%.

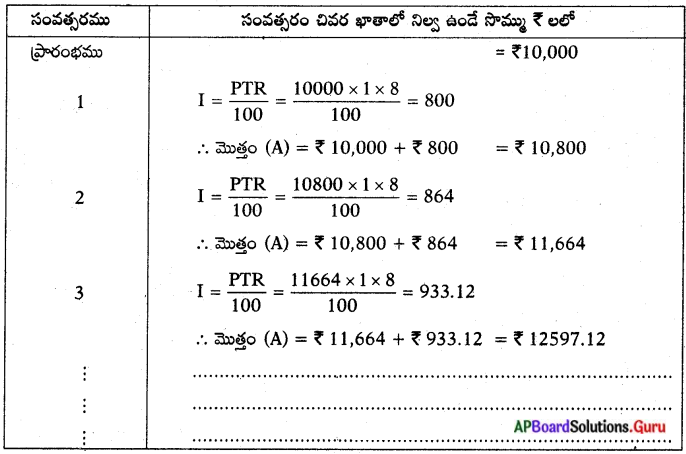
సంఖ్యల జాబితా 10,000, 10,800, 11,664, 12597.12, …………….
సామాన్యభేదం d = a₂ – a₁ = 10,800 – 10,000 = 800
a₃ – a₂ = 11,664 – 10,800 = 864
a₄ – a₃ = 12,597.12 – 11,664 = 933.12
అన్ని సందర్భాలలోనూ సామాన్య భేదం సమానంగా లేదు. కావున ఈ జాబితా అంకశ్రేణి కాదు.

ప్రశ్న 2.
అంకశ్రేఢుల యొక్క మొదటి పదము a మరియు సామాన్యభేదం d. విలువలు క్రింద ఇవ్వబడినవి. అయిన శ్రేణిలోని మొదటి నాలుగు పదాలను కనుగొనుము.
(i) a = 10, d = 10
సాధన.
మొదటి పదం a₁ = a = 10
రెండవ పదం a₂ = 10 + 10 = 20
మూడవ పదం a₃ = 20 + 10 = 30
నాల్గవ పదం a₄ = 30 + 10 = 40

(ii) a = – 2, d = 0
సాధన.
మొదటి పదం a₁ = a = – 2
రెండవ పదం a₂ = – 2 + 0 = – 2
మూడవ పదం a₃ = – 2 + 0 = – 2
నాల్గవ పదం a₄ = – 2 + 0 = – 2

(iii) a = 4, d = – 3
సాధన.
మొదటి పదం a₁ = a = 4
రెండవ పదం a₂ = 4 + (- 3) = 1
మూడవ పదం a₃ = 1 + (- 3) = – 2
నాల్గవ పదం a₄ = – 2 + (- 3) = – 5

(iv) a = – 1, d = 1/2
సాధన.
మొదటి పదం a₁ = a = – 1
రెండవ పదం a₂ = – 1 + \(\frac{1}{2}\) = \(-\frac{1}{2}\)
మూడవ పదం a₃ = – \(\frac{1}{2}\) + \(\frac{1}{2}\) = 0
నాల్గవ పదం a₄ = 0 + \(\frac{1}{2}\) = \(\frac{1}{2}\)

(v) a = – 1.25, d = – 0.25
సాధన.
మొదటి పదం a₁ = a = – 1.25
రెండవ పదం a₂ = – 1.25 + (- 0.25) = – 1.50
మూడవ పదం a₃ = (- 1.50) + (- 0.25) = – 1.75
నాల్గవ పదం a₄ = (- 1.75) + (- 0.25) = – 2.00 = – 2

ప్రశ్న 3.
క్రింద ఇవ్వబడిన అంకశ్రేఢులకు మొదటి పదమును, సామాన్య భేదంను కనుగొనుము.
(i) 3, 1, -1, -3, . . .
సాధన.
మొదటి పదం a = 3
సామాన్యభేదం d = a₂ – a₁ = 1 – 3 = – 2
[∵ d = a_k+1 – a_k]

(ii) – 5, – 1, 3, 7,…
సాధన.
మొదటి పదం a = – 5
సామాన్య భేదం d = a₂ – a₁ = (- 1) – (- 5)
= – 1 + 5 = 4.

(iii) \(\frac{1}{3}\), \(\frac{5}{3}\), \(\frac{9}{3}\), \(\frac{13}{3}\), …………
సాధన.
మొదటి పదం a = \(\frac{1}{3}\)
సామాన్యభేదం d = a₂ – a₁
= \(\frac{5}{3}\) – \(\frac{1}{3}\)
= \(\frac{4}{3}\)

(iv) 0.6, 1.7, 2.8, 3.9, ………….
సాధన.
మొదటి పదం a = 0.6
సామాన్యభేదం d = a₂ – a₁
= 1.7 – 0.6 = 1.1.

ప్రశ్న 4.
క్రింది జాబితాలలో ఏవి అంకశ్రేఢులు ? ఒకవేళ అంకశ్రేణి అయిన సామాన్య భేదం dను, తరువాత వచ్చే మూడు పదాలను కనుగొనుము.
(i) 2, 4, 8, 16, ……….
సాధన.
a₂ – a₁ = 4 – 2 = 2
a₃ – a₂ = 8 – 4 = 4
a₄ – a₃ = 16 – 8 = 8
…………………………………..
ప్రతి సందర్భంలోనూ సామాన్యభేదం సమానంగా లేదు. కావున ఈ జాబితా అంకశ్రేణి కాదు.

(ii) 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …………………..
సాధన.
a₂ – a₁ = \(\frac{5}{2}\) – 2
= \(\frac{5-4}{2}=\frac{1}{2}\)

a₃ – a₂ = 3 – \(\frac{5}{2}\)
= \(\frac{6-5}{2}=\frac{1}{2}\)

a₄ – a₃ = \(\frac{7}{2}\) – 3
= \(\frac{7-6}{2}=\frac{1}{2}\)
…………………………………………………………………………………
సామాన్యభేదం ప్రతి సందర్భంలోను సమానం. కావున ఈ జాబితా, అంకశ్రేడి (A. P.) అవుతుంది.
సామాన్యభేదం d = \(\frac{1}{2}\)
∴ తరువాత వచ్చే మూడు పదాలు
\(\frac{7}{2}+\frac{1}{2}\) = \(\frac{1}{2}\) = 4

4 + \(\frac{1}{2}\) = \(\frac{8+1}{2}=\frac{9}{2}\)

\(\frac{9}{2}+\frac{1}{2}\) = \(\frac{10}{2}\) = 5

(iii) – 1.2, – 3.2, – 5.2, – 7.2, ………….
సాధన.
a₂ – a₁ = (- 3.2) – (- 1.2) = – 3.2 + 1.2 = – 2
a₃ – a₂ = (- 5.2) – (- 3.2) = – 5.2 + 3.2 = -2
a₄ – a₃ = (- 7.2) – (- 5.2) = – 7.2 + 5.2 = – 2
సామాన్యభేదం అన్ని సందర్భాలలో సమానము.
కావున ఈ జాబితా అంకశ్రేఢి (A. P.) అవుతుంది.
సామాన్య భేదం d = – 2
∴ తరువాత వచ్చే మూడు పదాలు
– 7.2 + (- 2) = – 9.2
(- 9.2) + (- 2) = – 11.2
– 11.2 + (-2) = – 13.2.

(iv) – 10, – 6, – 2, 2, …………..
సాధన.
a₂ – a₁ = – 6 – (- 10) = – 6 + 10 = 4
a₃ – a₂ = – 2 -(- 6) = – 2 + 6 = 4
a₄ – a₃ = 2 – (-2) = 2 + 2 = 4
ప్రతి సందర్భంలోనూ సామాన్యభేదం సమానము.
కావున ఈ జాబితా అంకశ్రేణి (A.P) అవుతుంది.
సామాన్యభేదం d = 4
∴ తరువాత వచ్చే మూడు పదాలు
2 + 4 = 6
6 + 4 = 10
10 + 4 = 14.

(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2 ……….
సాధన.
a₂ – a₁ = 3 + √2 – 3 = √2
a₃ – a₂ = 3 + 2√2 – (3 + √2)
= 3 + 2√2 – 3 – √2 = √2
a₄ – a₃ = 3 + 2√2 – (3 – 2√2)
= 3 + 3√2 – 3 – 2√2 = √2
…………………………………..
ప్రతి సందర్భంలోనూ సామాన్యభేదం సమానము. కావున ఈ జాబితా అంకశ్రేణి (A.P) అవుతుంది. సామాన్యభేదం
d = √2
∴ తరువాత వచ్చే మూడు పదాలు
– 3 + 3√2 + √2 = 3 + 4√2
3 + 4√2 + √2 = 3 + 5√2
3 + 5√2 +√2 = 3 + 6√2.

(vi) 0.2, 0.22, 0.222, 0.2222, ………………
సాధన.
a₂ – a₁ = 0.22 – 0.2 = 0.02
a₃ – a₂ = 0.222 – 0.22 = 0.002
a₄ – a₃ = 0.2222 – 0.222 = 0.0002
ప్రతి సందర్భంలోను a_{k + 1} – a_k సమానము కాదు.
కావున ఈ జాబితా ఒక అంకశ్రేణి (A.P) ని సూచించదు.

(vii) 0, – 4, – 8, – 12, ……….
సాధన.
a₂ – a₁ = – 4 – 0 = – 4
a₃ – a₂ = – 8 – (- 4) = – 8 + 4 = -4
a₄ – a₃ = – 12 – (- 8) = – 12 + 8 = – 4
………………………………………………………………………..
…………………………………………………………………………
ప్రతి సందర్భంలోను a_{k + 1} – a_k, సమానము,
కావున ఈ జాబితా ఒక అంకశ్రేణి (A.P.) అవుతుంది.
సామాన్యభేదం d = – 4
∴ తరువాత వచ్చే మూడు పదాలు
– 12 + (- 4) = – 16
– 16 + (- 4) = – 20
– 20 + (- 4) = – 24.

(viii) \(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), …………
సాధన.
a₂ – a₁ = \(-\frac{1}{2}\) – (\(-\frac{1}{2}\)) = 0
a₃ – a₂ = 0
a₄ – a₃ = 0
……………………………………………………….
ప్రతి సందర్భంలోను a_k+1 – a_k, సమానము.
కావున ఈ జాబితా ఒక అంకశ్రేణి (A.P.) అవుతుంది.
సామాన్యభేదం d = 0
∴ తరువాత వచ్చే మూడు మాసాలు \(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), …………

(ix) 1, 3, 9, 27, ……………..
సాధన.
a₂ – a₁ = 3 – 1 = 2
a₃ – a₂ = 9 – 3 = 6
a₄ – a₃ = 27 – 9 = 18
………………………………………………….
ప్రతి సందర్భంలోను a_{k + 1} – a_k, సమానము కాదు.
కావున ఈ జాబితా ఒక అంకశ్రేణి (A.P.) కాదు.

(x) a, 2a, 3a, 4a, ……………….
సాధన.
a₂ – a₁ = 2a – a = a
a₃ – a₂ = 3a-2a = a
a₄ – a₃ = 4a – 3a = a
……………………………………………………………..
ప్రతి సందర్భంలోను a_{k + 1} – a_k సమానము.
కావున ఈ జాబితా ఒక అంకశ్రేఢి (A.P.) అవుతుంది. సామాన్యభేదం d = a
∴ తరువాత వచ్చే మూడు పదాలు 5a, 6a, 7a.

(xi) a, a², a³, a⁴ ………..
సాధన.
a₂ – a₁ = a² – a = a (a – 1)
a₃ – a₂ = a³ – a² = a² (a – 1)
a₄ – a₃ = a⁴ – a³ = a³ (a – 1)
……………………………………………………………….
ప్రతి సందర్భంలోను a_{k + 1} – a_k సమానము కాదు.
కావున ఈ జాబితా ఒక అంకశ్రేణిని (A.P.) కాదు.

(xii) √2, √8, √18, √32, ……………….
సాధన.
మొదటి పద్ధతి :
a₂ – a₁ = √8 – √2 = 2√2 – √2 = √2
a₃ – a₂ = √18 – √8 = 3√2 – 2√2 = √2
[∵ √8 = √4 × √2 = 2√2
√18 = √9 × √2 = 3√2
√32 = √16 × √2 = 4√2]
a₄ – a₃ = √32 – √18 = 4√2 – 3√2 = √2
………………………………………………………
∵ ప్రతి సందర్భంలోను a_{k + 1} – a_k సమానము. కావున ఈ జాబితా ఒక అంకశ్రేఢి (A. P.) అవుతుంది.
సామాన్యభేదం d = √2
∴ తరువాత మూడు పదాలు √32 + √2 = 4√2
= 5√2 = \(\sqrt{25 \times 2}\) = √50
√50 + √2 = 5√2 + √2
= 6√2 = \(\sqrt{36 \times 2}\) = √72
√72 + √2 = 6√2 + √2
= 7√2 = \(\sqrt{49 \times 2}\) = √98.

రెండవ పద్ధతి :
ఇచ్చిన జాబితా √2, √8, √18, √32, …………….
= √2, 2√2, 3√2, 4√2 …………….
√8 = \(\sqrt{4 \times 2}\) = 2√2
√18 = \(\sqrt{9 \times 2}\) = 3√2
√32 = \(\sqrt{16 \times 2}\) = 4√2
∴ a₂ – a₁ = 2√2 – √2 = √2
a₃ – a₂ = 3√2 – 2√2 = √2
a₄ – a₃ = 4√2 – 3√2 = √2
అన్ని సందర్భాలలోను a_{k + 1} – a_k సమానము.
కావున ఈ జాబితా ఒక అంకశ్రేణి (A.P.) అవుతుంది.
సామాన్యభేదం d = √2
తరువాత మూడు పదాలు 4√2 + √2 = 5√2 = \(\sqrt{25 \times 2}\) =√50
5√2 + √2 = 6√2 = \(\sqrt{36 \times 2}\)2 = √72
6√2 + √2 = 7√2 = \(\sqrt{49 \times 2}\) =√98 .

(xiii) √3, √6, √9, √12, ………….
సాధన.
a₂ – a₁ = √6 – √3 = √3(√2 – 1)
a₃ – a₂ = √9 – √6 = √3(3√3 – √2)
a₄ – a₃ = √12 – √9 = √3(2 – 3√3)
అన్ని సందర్భాలలోను a_{k + 1} – a_k సమానము కాదు.
కావున ఈ జాబితా ఒక అంకశ్రేఢి (A. P.) కాదు.