AP Board 10th Class Maths Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.3

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.3

ప్రశ్న 1.
10 సెం.మీ వ్యాసార్ధముగా గల వృత్తములో ఒక జ్యా కేంద్రము వద్ద లంబకోణాన్ని ఏర్పరిస్తే, కింది ఇవ్వబడిన వృత్తఖండాల వైశాల్యాలు కనుగొనండి. (π = 3.14 అని తీసుకోండి.)
(i) అల్ప వృత్తఖండము
(ii) అధిక వృత్త ఖండము
సాధన.

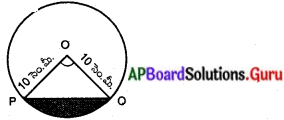
PQ జ్యా కేంద్రం వద్ద చేయు కోణం (x°) = 90°
వృత్త వ్యాసార్ధం (r) = 10 సెం.మీ.
(i) అల్ప వృత్త ఖండ వైశాల్యము = POQ సెక్టార్ వైశాల్యము – ∆POQ వైశాల్యము
POQ సెక్టార్ వైశాల్యము = \(\frac{x}{360}\) × πr²
∆POQ వైశాల్యము = \(\frac{1}{2}\) bh
∴ అల్ప వృత్త ఖండ వైశాల్యము = \(\frac{90}{360}\) × 3.14 × 10 × 10 – \(\frac{1}{2}\) × 10 × 10
= 78.5 – 50 = 28.5 సెం.మీ

(ii) అధిక వృత్తఖండ వైశాల్యము = వృత్త వైశాల్యము – అల్పవృత్త ఖండ వైశాల్యము.
= πr² – 28.5
= \(\frac{22}{7}\) × 10 × 10 – 28.5
= 314 – 28.5
∴ అల్ప వృత్త ఖండ వైశాల్యము = 285.5 సెం.మీ.

ప్రశ్న 2.
12 సెం.మీ వ్యాసార్ధముగా గల వృత్తములో ఒక జ్యా కేంద్రము వద్ద 120° కోణాన్ని ఏర్పరచింది. జ్యాతో ఏర్పడిన సంబంధిత అల్పవృత్త ఖండం యొక్క వైశాల్యమును కనుగొనండి. (π = 3.14 మరియు (√3 = 1.732 తీసుకోండి)
సాధన.
వృత్త వ్యాసార్ధం (r) = 12 సెం.మీ.
సెక్టార్ వైశాల్యం = \(\frac{x}{360}\) × πr²
చాపము వృత్త కేంద్రం వద్ద చేయు కోణం x° = 120°

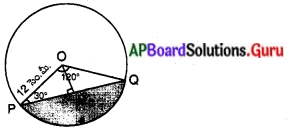
సెక్టార్ వైశాల్యం = \(\frac{120}{360}\) × 3.14 × 12 × 12
= 150.72 సెం.మీ .
‘O’ నుండి PQ పైకి లంబాన్ని గీయగా అది M వద్ద ఖండించినది ∆OPM = ∆OQM
[∵ OP = OQ వ్యాసార్థాలు ∠P = ∠Q (సమాన భుజాలకు ఎదురుగా ఉండు కోణాలు సమానాలు)
∠OMP = ∠OMQ భు.కో. భు నుండి అవి సరూపాలు)
∴ ∆OPQ వై.. = ∆OPM వై.. + ∆OQM వై|| –
= 2 ∆OPM వై||
∆OPM వై.. = \(\frac{1}{2}\) × PM × QM
కానీ cos 30° = \(\frac{\mathrm{PM}}{\mathrm{OP}}\)
[∵ ∆OPQ లో ∆POQ = 120°
= \(\frac{180^{\circ}-120^{\circ}}{2}=\frac{60^{\circ}}{2}\) = 30°]
⇒ \(\frac{\sqrt{3}}{2}=\frac{\mathrm{PM}}{12}\)
⇒ PM = \(\frac{12 \times \sqrt{3}}{2}\) = 6√3
అదే విధంగా, sin 30° = \(\frac{\mathrm{OM}}{\mathrm{OP}}\)
\(\frac{1}{2}=\frac{\text { OM }}{12}\)
⇒ OM = 6 సెం.మీ.
∴ ∆ OPM వైశాల్యం = \(\frac{1}{2}\) × 6√3 × 6 = 18√3
= 18 × 1.732 = 31.176 సెం.మీ²
∴ ∆OPQ వైశాల్యము = 2 × 31.176
= 62.352 సెం.మీ²
∴ అల్ప వృత్తఖండ వైశాల్యం PQ = POQ సెక్టార్ వైశాల్యం – ∆OPQ వైశాల్యం
= 150.72 – 62.352 = 88.368 సెం.మీ²

ప్రశ్న 3.
ఒక కారు అద్దముపై ఒకదానిపై అధ్యారోహణము (overlap) కాని నీటిని తుడిచే రెండు వైపర్లు వున్నాయి. ప్రతి వైపర్ పొడవు 25 సెం.మీ. 115° కోణముతో నీటిని తుడుస్తున్నది. ఒకేసారి రెండు వైపర్లు పనిచేయు సందర్భములో మొత్తం అద్దాన్ని శుభ్రపరిచే ప్రదేశ వైశాల్యము కనుగొనుము. (π = \(\frac{22}{7}\) అని తీసుకోండి.)
సాధన.

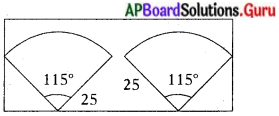
ప్రతి వైపర్ చేయు కోణం = 115°
రెండు వైపర్లు అద్దాన్ని శుభ్రపర్చు వైశాల్యం = వైపర్లు ఏర్పర్చు రెండు సెక్టార్ల వైశాల్యాల మొత్తం.
= 2 × \(\frac{x}{360}\) × πr²
= 2 × \(\frac{115^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 25 × 25
= \(\frac{230}{360} \times \frac{22}{7}\) × 25 × 25
= 1254.96 = 1255 సెం.మీ²

ప్రశ్న 4.
క్రింది పటములో ABCD చతురస్రం యొక్క భుజము 10 సెం.మీ పొడవు కలిగి వున్నది మరియు చతురస్రభుజము వ్యాసముగా గల అర్ధవృత్తాలు ప్రతిభుజము వైపున గీయబడ్డాయి. షేడ్ చేయబడిన ప్రదేశ వైశాల్యము కనుగొనుము. (π = 3.14 అని తీసుకోండి).

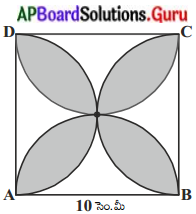
సాధన.
పటం నుండి షేడ్ చేయని భాగాలను I, II, III, IV లుగా గుర్తింపుము.

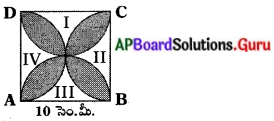
Iవ ప్రాంత వైశాల్యం + III వ ప్రాంత వైశాల్యం = ABCD చతురస్ర వైశాల్యం – 5 సెం.మీ.
వ్యాసార్ధం గల రెండు అర్ధవృత్తాల వైశాల్యాలు = 10 × 10 – 2 × \(\frac{1}{2}\) × π × 5²
= 100 – 78.5 = 21.5 సెం.మీ²
అదే విధంగా II ప్రాంత వై + IV వ ప్రాంత వై = 21.5 సెం.మీ²
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = ABCD చతురస్ర వై| – షేడ్ చేయని 4 ప్రాంతాల వైశాల్యాల మొత్తం
= 100 – 2 × 21.5 = 100 – 43 = 57 సెం.మీ²

ప్రశ్న 5.
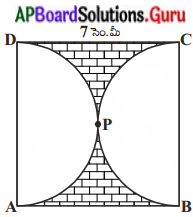
పటంలో ABCD చతురస్రభుజము 7 సెం.మీ మరియు APD మరియు BPC లు అర్ధవృత్తములు అయిన షేడ్ చేసిన ప్రదేశవైశాల్యము కనుగొనుము. (π = \(\frac{22}{7}\) ను తీసుకోండి).

సాధన.
షేడ్ చేయబడిన ప్రాంత వైశాల్యం = ABCD చతురస్ర వైశాల్యం, 3. 5 సెం.మీలు వ్యాసార్ధం గల రెండు అర్ధ వృత్తాల వై॥ల మొత్తం.
= 7 × 7 – 2 × \(\frac{1}{2}\) × \(\frac{22}{7}\) × 3.5 × 3.5
= 49 – 38.5 = 10.5 సెం.మీ.²

ప్రశ్న 6.
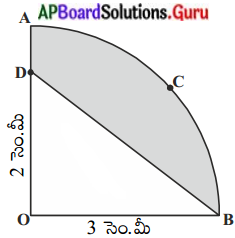
పటములో 0 కేంద్రము మరియు 3.5 సెం.మీ వ్యాసార్ధముగా గల వృత్తములో OACB అనేది ఒక సెక్టరు పాదము OD = 2 సెం.మీ అయిన షేడ్ చేసిన ప్రాంత వైశాల్యము కనుగొనుము. (π = \(\frac{22}{7}\) అని తీసుకోండి)

సాధన.
OACD అనునది వృత్తంలోని 4వ భాగం గల ఒక సెక్టార్. షేడ్ చేయబడిన ప్రాంత వైశాల్యం = సెక్టార్ వైశాల్యం – ∆BOD వైశాల్యం
= \(\frac{x}{360}\) × πr² – \(\frac{1}{2}\) . OB . OD
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × 3.5 × 3.5 – \(\frac{1}{2}\) × 3.5 × 2
= 9.625 – 3.5 = 6.125 సెం.మీ.

ప్రశ్న 7.
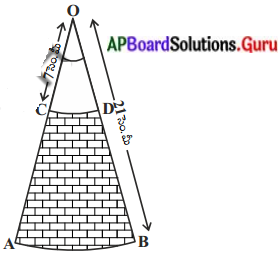
‘0’ కేంద్రముగా గల రెండు ఏక కేంద్ర వృత్తాల వ్యాసార్ధాలు వరుసగా 21 సెం.మీ మరియు 7 సెం.మీ మరియు AB, CD లు రెండు చాపరేఖలు (పటము చూడండి). ∠AOB = 30° అయిన షేడ్ చేసిన ప్రదేశ వైశాల్యమును కనుగొనండి. (π = \(\frac{22}{7}\) తీసుకోండి)

సాధన.
షేడ్ చేయబడిన భాగము వైశాల్యం = AOB సెక్టార్ వైశాల్యం – OCD సెక్టార్ వైశాల్యం
= \(\frac{30}{360} \times \frac{22}{7}\) × 21 × 21 – \(\frac{30}{360} \times \frac{22}{7}\) × 7 × 7
[∵ సెక్టార్ వైశాల్యం = \(\frac{x}{360}\) × πr²)
= \(\frac{1}{12}\) × \(\frac{22}{7}\) [441 – 49]
= \(\frac{22}{84}\) × 392 = 102.66 సెం.మీ².

ప్రశ్న 8.
పటంలో వ్యాసార్ధము 10 సెం.మీ గా గల వృత్తంలో రెండు సెక్టరు పాదముల మధ్య ఏర్పడిన ఉమ్మడి ప్రదేశం (షేడ్ చేయబడినది) యొక్క వైశాల్యమును కనుగొనండి. (π = 3.14 అని తీసుకోండి)

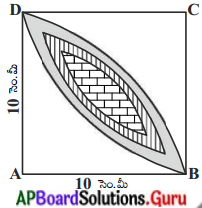
సాధన.
చాపానికి ఇరువైపులా P, Qబిందువులను గుర్తింపుము.
ABCD చతురస్ర కర్ణం BD అనుకొనుము.
DPB వృత్త ఖండ వైశాల్యం = ∆DPB సెక్టార్ వై! – ∆ABD వైశాల్యం
= \(\frac{x}{360}\) × πr² – \(\frac{1}{2}\) bh
= \(\frac{90}{360}\) × \(\frac{22}{7}\) × 10 × 10 – \(\frac{1}{2}\) × 10 × 10
= 78.57 – 50 = 28.5 సెం.మీ.
అదే విధంగా DQB వృత్త ఖండ వైశాల్యం = 28.5 సెం.మీ
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం= (DPB + DQB)
వృత్త ఖండాల వైశాల్యాలు = 28.5 + 28.5 = 57 సెం.మీ (లేదా)
చతురస్ర భుజం = 10
చతురస్ర వైశాల్యం = 10 × 10 = 100 సెం.మీ
A, C లు కేంద్రాలుగా గల 10 సెం.మీ వ్యాసార్ధాలుగా గల రెండు సెక్టార్ల వైశాల్యాలు = 2 × \(\frac{90}{360}\) × \(\frac{22}{7}\) × 10 × 10
= \(\frac{1100}{7}\) = 157.14 సెం.మీ
షేడ్ చేయబడిన ప్రాంతం రెండింటికి ఉమ్మడి ప్రాంతం
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = రెండు సెక్టార్ల వైశాల్యం – చతురస్ర వైశాల్యం = 157 – 100 = 57 సెం.మీ².