SCERT AP 7th Class Maths Solutions Pdf Chapter 3 సామాన్య సమీకరణాలు Ex 3.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 3rd Lesson సామాన్య సమీకరణాలు Exercise 3.3
ప్రశ్న 1.
క్రింది సమీకరణాలను సాధించి, సాధనను సరిచూడండి.
(i) 5x – 17 = 18
సాధన.
5x – 17 = 18
⇒ 5x = 18 + 17 (- 17 ను పక్షాంతరం చేయగా)
⇒ 5x = 35
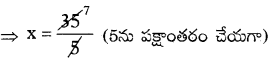
⇒ x = 7
సరిచూచుట: x = 7 ను ఇచ్చిన సమీకరణం
5x – 17 = 18 లో ప్రతిక్షేపించగా
LHS = 5x – 17
= 5(7) – 17
= 35 – 17 = 18 = RHS
∴ LHS = RHS
![]()
(ii) 29 – 7y = 1
సాధన.
29 – 7y = 1
⇒ – 7y = 1 – 29 (29 ని పక్షాంతరం చేయగా)
⇒ – 7y = – 28
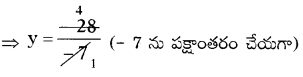
⇒ y = 4
సరిచూచుట: y = 4 ను ఇచ్చిన సమీకరణం 29 – 7y = 1లో ప్రతిక్షేపించగా
LHS = 29 – 7y
= 29 – 7(4)
= 29 – 28 = 1 = RHS
∴ LHS = RHS
(iii) a – 2.3 = 1.5
సాధన.
a – 2.3 = 1.5
= a = 1.5 + 2.3 (2.3 ని పక్షాంతరం చేయగా)
⇒ a = 3.8
సరిచూచుట : LHS = a – 2.3
= 3.8 – 2.3
= 1.5 = RHS
∴ LHS = RHS
(iv) b + 3\(\frac{1}{2}\) = \(\frac{7}{4}\)
సాధన.

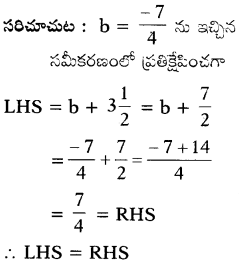
![]()
(v) \(\frac{7 p}{10}\) + 9 = 15
సాధన.
\(\frac{7 p}{10}\) + 9 = 15
⇒ \(\frac{7 p}{10}\) = 15 – 9 [9 ను పక్షాంతరం చేయగా]
⇒ \(\frac{7 p}{10}\) = 6
⇒ 7p = 6 × 10 [\(\frac{1}{10}\) ను పక్షాంతరం చేయగా]
⇒ 7p = 60
⇒ p = \(\frac{60}{7}\)

(vi) 6(q – 5) = 42
సాధన.
6(q – 5) = 42
⇒ 6q – 30 = 42
⇒ 6q = 42 + 30 [- 30 ను పక్షాంతరం చేయగా]
⇒ 6q = 72

⇒ q = 12
సరిచూచుట: q = 12 ను ఇచ్చిన
సమీకరణంలో ప్రతిక్షేపించగా
LHS = 6(q – 5)
= 6(12 – 5)
= 6(7) = 42 = RHS
∴ LHS = RHS
![]()
(vii) – 3(m + 5) + 1 = 13
సాధన.
– 3(m + 5) + 1 = 13
⇒ – 3m – 15 + 1 = 13
⇒ – 3m – 14 = 13
⇒ – 3m = 13 + 14 [- 14 ను పక్షాంతరం చేయగా]
⇒ – 3m = 27
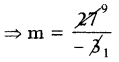
⇒ m = – 9
సరిచూచుట : m = – 9 ని ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = – 3(m + 5) + 1
= – 3(- 9 + 5) + 1
= – 3 (- 4) + 1
= 12 + 1 = 13 = RHS
∴ LHS = RHS
(viii) \(\frac{n}{2}+\frac{n}{3}+\frac{n}{5}\) = 31
సాధన.

సరిచూచుట: n = 30 ని ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = \(\frac{\mathrm{n}}{2}+\frac{\mathrm{n}}{3}+\frac{\mathrm{n}}{5}\)
= \(\frac{30}{2}+\frac{30}{3}+\frac{30}{5}\)
= 15 + 10 + 6
= 31
= RHS
∴ LHS = RHS
![]()
ప్రశ్న 2.
కింది సమీకరణాలను సాధించి, సాధనను సరిచూడండి.
(i) 3(p -7) – 4 = 5
సాధన.
3(p -7) – 4 = 5
⇒ 3p – 21 – 4 = 5
⇒ 3p – 25 = 5
⇒ 3p = 5 + 25
⇒ 3p = 30
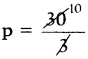
⇒ p = 10
సరిచూచుట: p = 10 ని ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = 3(p – 7) – 4
= 3(10 – 7) – 4
= 3 × (3) – 4
= 9 – 4 = 5 = RHS
∴ LHS = RHS
(ii) 5(q – 3) – 3(q – 2) = 0
సాధన.
5(q – 3) – 3(q – 2) = 0
⇒ 5q – 15 – 3q + 6 = 0
⇒ 24 – 9 = 0
⇒ 2q = 0 + 9
⇒ 2q = 9
⇒ q = \(\frac{9}{2}\)
సరిచూచుట: q = \(\frac{9}{2}\) ను ఇచ్చిన
సమీకరణంలో ప్రతిక్షేపించగా
LHS = 5(q – 3) – 3(q – 2)
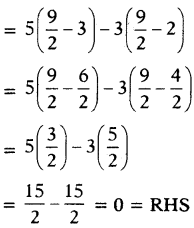
∴ LHS = RHS
![]()
(iii) 0.4x – 0.3x – 1.2 = 0.6
సాధన.
0.45 – 0.3x – 1.2 = 0.6
⇒ 0.1 x – 1.2 = 0.6
⇒ 0.1 x = 0.6 + 1.2
⇒ 0.1 x = 1.8
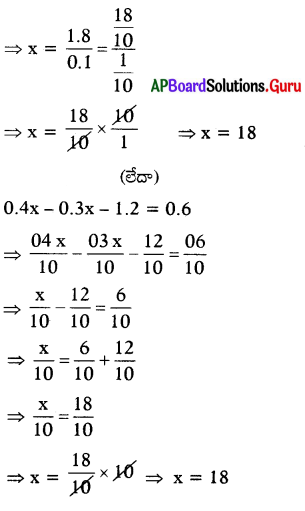
సరిచూచుట: x = 18 ని ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = 0.45 – 0.3x – 1.2
= 0.4(18) – 0.3(18) – 1.2
= 7.2 – 5.4 – 1.2
= 7.2 – 6.6
= 0.6 = RHS
∴ LHS = RHS
(iv) 4(3y + 4) = 7.6
సాధన.
4(3y + 4) = 7.6
⇒ 12y + 16 = 7.6
⇒ 12y = 7.6 – 16
⇒ 12y = – 8.4
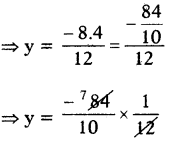
⇒ y = \(\frac{-7}{10}\)
⇒ y = – 0.7
సరిచూచుట: y = – 0.7 ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = 4(3y + 4)
= 4[3 (- 0.7) + 4]
= 4[- 2.1 + 4]
= 4 [1.9]
= 7.6 = RHS
∴ LHS = RHS
![]()
(v) 20 – (2r – 5) = 25
సాధన.
20 – (2r- 5) = 25 –
⇒ 20 – 2x + 5 = 25
⇒ 25 – 2r = 25
⇒ – 2r = 25 – 25
⇒ – 2r = 0
⇒ r = \(\frac{0}{2}\)
⇒ r = 0
సరిచూచుట: r = 0 ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = 20 – (2r-5)
= 20 – [2(0) – 5]
= 20 – [0 – 5]
= 20 – (-5)
= 20 + 5 = 25 = RHS
∴ LHS = RHS
(vi) 3(5 – t) – 2(t – 2) = -1
సాధన.
3(5 – t) – 2(t – 2) = – 1
= 15 – 3t – 2t + 4 = – 1
⇒ 19 – 5t = – 1
⇒ – 5t = – 1 – 9
⇒ – 5t = – 20
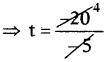
⇒ t = 4
సరిచూచుట: t = 4 ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = 3(5 – t) – 2(t – 2)
= 3(5 – 4) – 2(4 – 2)
= 3(1) – 2(2)
= 3 – 4 = – 1 = RHS
∴ LHS = RHS
![]()
(vii) 3(2k + 1) – 2(k – 5) – 5(5 – 2k) = 16
సాధన.
3(2k + 1) – 2(k – 5) – 5(5 – 2k) = 16
⇒ 6k + 3 – 2k + 10 – 25 + 10k = 16
⇒ 16k – 2k + 13-25 = 16
⇒ 14k – 12 = 16
⇒ 14k = 16 + 12
⇒ 14k = 28
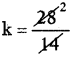
⇒ k = 2
సరిచూచుట: k = 2 ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
LHS = 3(2k + 1) – 2(k – 5) – 5(5 – 2k)
= 3[2(2) + 1] – 2[(2) – 5] – 5[5 – 2(2)]
= 3[4 + 1] – 2(-3) – 5(5 – 4)
= 3[5] + 6 – 5(1)
= 15 + 6 – 5
= 21 – 5 = 16 = RHS
∴ LHS = RHS
(viii) \(\frac{3 \mathrm{~m}}{4}\) – 5m – \(\frac{3}{4}\) = 12
సాధన.

సరిచూచుట: m = – 3 ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా.

= – 3 + 15 = 12 = RHS
∴ LHS = RHS
![]()
(ix) \(\frac{4 n}{5}+\frac{n}{4}-\frac{n}{2}=\frac{11}{10}\)
సాధన.

సరిచూచుట: n = 2 ను ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా.
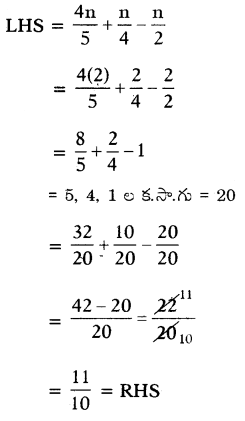
∴ LHS = RHS
![]()
(x) \(\frac{x}{2}-\frac{4}{5}+\frac{x}{5}+\frac{3 x}{10}=\frac{1}{5}\)
సాధన.

సరిచూచుట: x = 1 ని ఇచ్చిన సమీకరణంలో ప్రతిక్షేపించగా
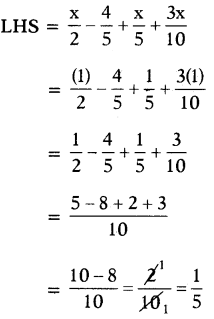
= RHS
∴ LHS = RHS
![]()
ప్రశ్న 3.
x = 2 సాధన కలిగిన ఏవైనా మూడు సమాన సమీకరణాలు వ్రాయండి.
సాధన.

ప్రశ్న 4.
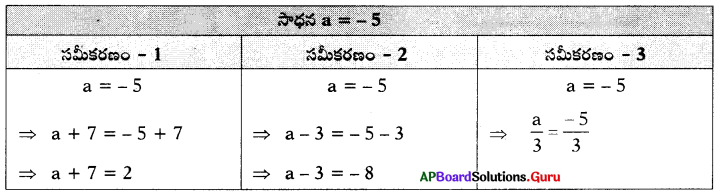
a = – 5 సాధన కలిగిన ఏవైనా మూడు సమాన సమీకరణాలు వ్రాయండి.
సాధన.