AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.3 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.3
![]()
Question 1.
Draw the following triangles and construct circumcircles for them.
(OR)
In ΔABC, AB = 6 cm, BC = 7 cm and ∠A = 60°.
Construct a circumcircle to the triangle XYZ given XY = 6cm, YZ = 7cm and ∠Y = 60°. Also, write steps of construction.
Solution:
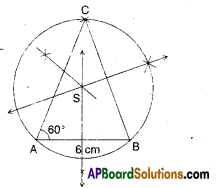
Steps of construction :
- Draw the triangle with given mea-sures.
- Draw perpendicular bisectors to the sides.
- The point of concurrence of per-pendicular bisectors be S’.
- With centre S; SA as radius, draw a circle which also passes through B and C.
- This is the required circumcircle.
ii) In ΔPQR; PQ = 5 cm, QR = 6 cm and RP = 8.2 cm.
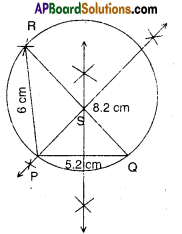
Steps of construction:
- Draw ΔPQR with given measures.
- Draw perpendicular to PQ, QR and RS; let they meet at ‘S’.
- With S as centre and SP as radius draw a circle.
- This is the required circumcircle.
iii) In ΔXYZ, XY = 4.8 cm, ∠X = 60°and ∠Y = 70°.
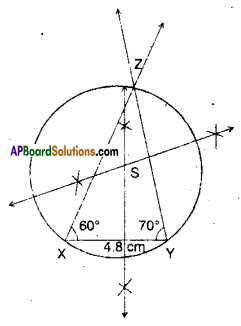
Steps of construction:
- Draw ΔXYZ with given measures.
- Draw perpendicular bisectors to the sides of ΔXYZ, let the point of con-currence be S’.
- Draw the circle (S, \(\overline{\mathrm{SX}}\)).
- This is the required circumcircle.
![]()
Question 2.
Draw two circles passing A, B where AB = 5.4 cm.
(OR)
Draw a line segment AB with 5.4 cm. length and draw two different circles that passes through both A and B.
Solution:
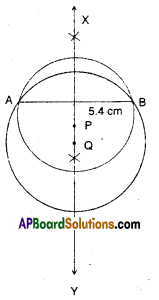
Steps of construction:
- Draw a line segment AB = 5.4 cm.
- Draw the perpendicular bisector \(\stackrel{\leftrightarrow}{X Y}\) of AB.
- Take any point P on \(\stackrel{\leftrightarrow}{X Y}\).
- With P as centre and PA as radius draw a circle.
- Let Q be another point on XY.
- Draw the circle (Q, \(\overline{\mathrm{QA}}\)).
Question 3.
If two circles intersect at two points, then prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
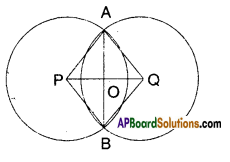
Let two circles with centre P and Q intersect at two distinct points say A and B.
Join A, B to form the common chord
\(\overline{\mathrm{AB}}\). Let ‘O’ be the midpoint of AB.
Join ‘O’ with P and Q.
Now in ΔAPO and ΔBPO
AP = BP (radii)
PO = PO (common)
AO = BO (∵ O is the midpoint)
∴ ΔAPO ≅ ΔBPO (S.S.S. congruence)
Also ∠AOP = ∠BOP (CPCT)
But these are linear pair of angles.
∴ ∠AOP = ∠BOP = 90°
Similarly in ΔAOQ and ΔBOQ
AQ = BQ (radii)
AO = BO (∵ O is the midpoint of AB)
OQ = OQ (common)
∴ AAOQ ≅ ABOQ
Also ∠AOQ = ∠BOQ (CPCT)
Also ∠AOQ + ∠BOQ = 180° (linear pair of angles)
∴ ∠AOQ = ∠BOQ = \(\frac{180^{\circ}}{2}\) = 90°
Now ∠AOP + ∠AOQ = 180°
∴ PQ is a line.
Hence the proof.
![]()
Question 4.
If two intersecting chords of a circle make equal angles with diameter pass¬ing through their point of intersection, prove that the chords are equal.
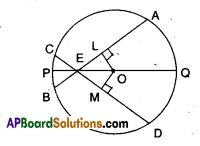
Solution:
Let ‘O’ be the centre of the circle.
PQ is a drametre.
\(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are two chords meeting at E, a point on the diameter.
∠AEO = ∠DEO
Drop two perpendiculars OL and OM from ‘O’ to AB and CD;
Now in ΔLEO and ΔMEO
∠LEO = ∠MEO [given]
EO = EO [Common]
∠ELO = ∠EMO [construction 90°]
∴ ΔLEO ≅ ΔMEO
[ ∵ A.A.S. congruence]
∴ OL = OM [CPCT]
i.e., The two chords \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are at equidistant from the centre ‘O’.
∴ AB = CD
[∵ Chords which are equi-distant from the centre are equal]
Hence proved.
![]()
Question 5.
In the given figure, AB is a chord of circle with centre ‘O’. CD is the diam-eter perpendicular to AB. Show that AD = BD.
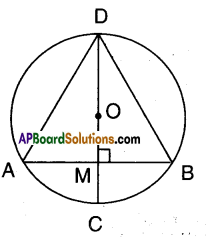
Solution:
CD is diameter, O is the centre.
CD ⊥ AB; Let M be the point of inter-section.
Now in ΔAMD and ΔBMD
AM = BM [ ∵ radius perpendicular to a chord bisects it]
∠AMD =∠BMD [given]
DM = DM (common)
∴ ΔAMD ≅ ΔBMD
⇒ AD = BD [C.P.C.T]