Andhra Pradesh BIEAP AP Inter 1st Year Chemistry Study Material 7th Lesson Chemical Equilibrium and Acids-Bases Textbook Questions and Answers.
AP Inter 1st Year Chemistry Study Material 7th Lesson Chemical Equilibrium and Acids-Bases
Very Short Answer Questions
Question 1.
State law of chemical equilibrium.
Answer:
The ratio of product of molar concentrations of the products to the product of molar concentrations of the reactants has a constrant value. This is known as the equilibrium law (or) law of chemical equilibrium.
Question 2.
Can equilibrium be achieved between water and its vapours in an open vessel. Explain.
Answer:
Equilibrium does not acheived between water and its vapour in an open vessel.
But the equilibrium achieved between water and its vapour in a closed vessel.
H2Ol) ⇌ H2O(g)
![]()
Question 3.
Why the concentrations of pure liquids and pure solids are ignored from equilibrium constant expressions ?
Answer:
The concentrations of pure solids and pure liquids are ignored from equilibrium constant expres-sions because the concentrations of pure solids and pure liquids are taken as unity.
Question 4.
What is homogenous equilibrium ? Write two homogenous reactions.
Answer:
It the physical states of the participating substances are same they the equilibrium is homogeneous equilibrium
e.g.: H2(g) + I2(g) ⇌ 2HI(g))
N2(g) + 3H2(g) ⇌ 2NH3(g)
Question 5.
What is heterogeneous equilibrium? Write two heterogeneous reactions.
Answer:
If the physical states of all (or) some of the participating substances are same then the equilibrium is Heterogeneous equilibrium.
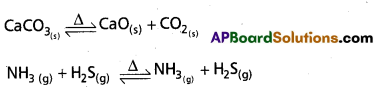
Question 6.
Write reaction quotient, Q, for each of the following reactions.
a) 3O2(g) ⇌ 2O3(g)
b) 4NH3(g) + 7O2(g) ⇌ 4NO2(g) + 6H2O(g)
Answer:
a) 3O2(g) ⇌ 2O3(g)
Q = \(\frac{\left(\mathrm{O}_3\right)_{\mathrm{t}}^2}{\left(\mathrm{O}_2\right)_{\mathrm{t}}^2}\)
b) 4NH3(g) + 7O2(g) ⇌ 4NO2(g) + 6H2O(s)
Q = \(\frac{\left[\mathrm{NO}_2\right]_t^4\left[\mathrm{H}_2 \mathrm{O}\right]_t^6}{\left[\mathrm{NH}_3\right]_t^4\left[\mathrm{O}_2\right]_t^7}\)
![]()
Question 7.
Define equilibrium constant.
Answer:
The ratio of product of molar concentrations of products to the product of molar concentrations of reactants is called equilibrium constant (Kc)
Question 8.
The equilibrium constant expression for a gas reaction is Kc = \(\frac{\left[\mathrm{NH}_3\right]^4\left[\mathrm{O}_2\right]^5}{[\mathrm{NO}]^4\left[\mathrm{H}_2 \mathrm{O}\right]^6}\) Write the balanced chemical equation corresponding to this expression.
Answer:
Given Kc = \(\frac{\left[\mathrm{NH}_3\right]^4\left[\mathrm{O}_2\right]^5}{[\mathrm{NO}]^4\left[\mathrm{H}_2 \mathrm{O}\right]^6}\)
Balanced chemical equation is
4NO + 6H2O ⇌ 4NH3 + 5O2
Question 9.
Write the relation between Kp and Kc.
Answer:
Kp = Kc(RT)∆n
∆n = No. of gaseous products – No. of gaseous reactants
R = Universal gas constant
Question 10.
Under what conditions for a reaction Kp and Kc are numerically equal?
Answer:
If ∆n = 0 i.e. No. of gaseous products = No. of gaseous reactants
then Kp = Kc (RT)∆n
Kp = Kc(RT)0
then Kp = Kc
Question 11.
Give two chemical equilibrium reactions for which Kp = Kc
Answer:
- H2(g) + I2(g) ⇌ 2 HI(g)
Here ∆n = 0
∴ Kp = Kc - N2(g) + O2(g) ⇌ 2NO(g)
Here ∆n = 0
∴ Kp = Kc
![]()
Question 12.
Give two chemical equilibrium reactions for which Kp > Kc.
Answer:
1) 2NH3(g) ⇌ N2(g) + 3H2(g)
∆n = np – nR = (3 + 1) – 2 = 2
∆n = 2 (+ve)
∴ Kp > Kc
2) 2SO3(g) ⇌ 2SO2(g) + O2(g)
∆n = np – nR = (2 + 1) – 2 = 1
∆n = 1 (+ve)
∴ Kp > Kc
Question 13.
Give two chemical equilibrium reactions for which Kp < Kc
Answer:
1) N2(g) + 3H2(g) ⇌ 2NH3(g)
∆n = np – nR = 2 – (1 + 3) = -2
∆n = -2 (- ve)
∴ Kp < Kc
2) 2SO2(g) + O2(g) ⇌ 2SO3(g)
∆n = np – nR
= 2 – (1 + 2) = -1
∆n = -1 (-ve)
∴ Kp < Kc
Question 14.
Write the equations for the conversion of Kc to Kp for each of the following reactions.
a) CO(g) + H2O (g) ⇌ CO2 (g) + H2 (g)
b) C3H8(g) + 5O2(g) ⇌ 3CO2 (g) + 4H2O (g)
Answer:
a) CO(g) + H2O(g) ⇌ CO2(g) + H2(g)
Kp = \(\frac{\mathrm{P}_{\mathrm{CO}_2} \times \mathrm{P}_{\mathrm{H}_2}}{\mathrm{P}_{\mathrm{CO}} \times \mathrm{P}_{\mathrm{H}_2 \mathrm{O}}}\)
Kc = \(\frac{\left[\mathrm{CO}_2\right]\left[\mathrm{H}_2\right]}{[\mathrm{CO}]\left[\mathrm{H}_2 \mathrm{O}\right]}\)
Kc to Kp conversion
b) C3H8(g) + 5O2(g) ⇌ 3CO2 (g) + 4H2O (g)
Kp = \(\frac{\mathrm{P}_{\mathrm{CO}_2}^3 \times \mathrm{P}_{\mathrm{H}_2 \mathrm{O}^4}}{\mathrm{P}_{\mathrm{C}_3 \mathrm{H}_8} \times \mathrm{P}_{\mathrm{O}_2}^5}\)
Kc = \(\frac{\left[\mathrm{CO}_2\right]^3\left[\mathrm{H}_2 \mathrm{O}\right]^4}{\left[\mathrm{C}_3 \mathrm{H}_8\right]\left[\mathrm{O}_2\right]^5}\)
Kc to Kp conversion
![]()
Question 15.
What are the factors which influence the chemical equilibrium?
Answer:
The factors influencing chemical equilibrium are
- Concentration of reactants and the products
- Temperature of reaction
- Pressure of reaction
- Inert gas addition etc.
Question 16.
What is the effect of pressure on a gaseous chemical equilibrium?
Answer:
Increase of external pressure of the reaction at equlibrium favours the reaction in the direction in which the volume (or) the No. of molecules decreases.
Decrease of external pressure of reaction at equilibrium favour the reaction in the direction in which the volume (or) no. of molecules increase.
Question 17.
What is the effect of increase in concentration of reactants of a chemical reaction at equilibrium?
Answer:
Increase of concentration of the reactants in the reaction mixture at equilibrium favours the forward reaction (Reactants → products)
Question 18.
Can catalyst disturb the state of equilibrium?
Answer:
Addition of catalyst to the reaction does not effect the equilibrium position. It only speedy up the attainment of the equilibrium.
Question 19.
On which factor, the equilibrium constant value changes?
Answer:
The numerical value of equilibrium constant depends on the standard state of products and reactants chosen.
Question 20.
The equilibrium constants of a reaction at 27° C and at 127°C are 1.6 × 10-3 and 7.6 × 10-2 respectively. Is the reaction exothermic or endothermic.
Answer:
Given equilibrium constants
At 27°C – 1.6 × 10-3
At 127°C -7.6 × 10-2
From the above values as the temperature raised euilibrium constant value increased. Here ∆H = +ve
∴ The reaction is endothermic.
![]()
Question 21.
What is the effect of temperature on a system at equilibrium?
Answer:
- Increase in temperature of the reaction mixture at equilibrium favours the endothermic reaction.
- Decrease in temperature of the reaction mixture at equilibrium favours the exothermic reaction.
Question 22.
For an exothermic reaction, what happens to the equilibrium constant if temperature is raised?
Answer:
For an exothermic reaction when the temperature is raised equilibrium constant value decreased.
Question 23.
What kind of equilibrium constant can be calculated form ∆G° value for a reaction involving only gases?
Answer:
Mathematical expression in the thermodynamic view of equilibrium is
∆G = ∆G° + RTlnQ
At equilibrium ∆G = 0 and Q = K
∴ ∆G = ∆G° + RTlnK = 0
∆G° = -RTlnK
knK = \(\frac{-\Delta G^{\circ}}{R}\)
K = e-∆G°/RT
K = Equilibrium constant using the above equation the sponteinity of reaction can be predicted.
Question 24.
What is a Bronsted base ? Give one example.
Answer:
The substance which accepts a proton from the other substance is called Bronsted base
e.g.: NH3, H2O etc.
Qeustion 25.
What is Lewis acid ? Give one example.
Answer:
A substance which can accept an electron pair to from a co-ordinate covalent bond with donor is called Lewis acid.
e.g. : H+, BF3, SnCl2 etc.
Question 26.
What is meant by ionic product of water ?
Answer:
At a given temp, the product of the concentrations of H+ and OH– ions in water is called ionic product
Ionic product Kw = [H+] [OH–]
At 25°C Kw = 1.008 × 10-14 mole2/lit2
![]()
Question 27.
What is the value of Kw? What are its units ?
Answer:
At 25°C Ionic product of water Kw = 1.008 × 10-14 mole2/lit2
Units : mole2/lit2
Question 28.
What is the effect of temperature on ionic product of water ?
Answer:
As the temperature increases ionisation of water increases and hence Ionic product alue (Kw) also increases.
Question 29.
H2O + H2O ⇌ H2O+ + OH–
The ionic product of water is 1 × 10-14 at 25°C and 3.0 × 10-14 at 40°C.
Is the above process endothermic or exothermic ?
Answer:
Given reaction
H2O + H2O ⇌ H2O+ + OH–
Kwat25°C – 1 × 10-14 mole2/lit2
Kwat40°C – 3 × 10-14 mole2/lit2
The above reaction is endo thermic reaction because Kw value increases with increase of temperature.
Question 30.
All Bronsted bases are Lewis bases. Explain.
Answer:
Bronsted base means proton acceptor and lewis base means electron pair donor.
But according to two theories base provides a lone pair.
∴ All bronsted bases are lewisbases
Question 31.
All Lewis acids are not Bronsted acids. Why ?
Answer:
- Lewis acid means electron pair acceptor and bronsted acid means proton donar.
- According to Lewis concept many acids donot have proton.
So all Lewis acids are not Bronsted bases.
![]()
Question 32.
What is degree of ionization?
Answer:
- It is the expression used to find the extent of ionisation of electrolytes.
- It is devoted by ‘α’.
Question 33.
What is the measure of strength of an acid and base ?
Answer:
- Strength of an acid can be measured by the acid disociation constant (Ka)
- Strength of a base can be measured by the base disaciating constant (kb)
Question 34.
Give two examples of salts whose aqueous solutions are basic.
Answer:
Sodium acetate (CH3COONa), Sodium carbonate (Na2CO3) salts aqueous solutions are basic in nature due to anionic hydrolysis.
Question 35.
Give two examples of salts whose aqueous solutions are acidic.
Answer:
Ammonium chloride (NH4Cl), Ammonium sulphate [(NH4)2 SO4] salts aqueous solutions are acidic in nature.
Question 36.
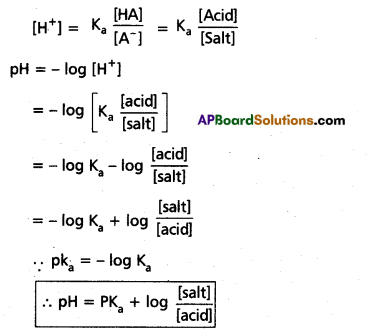
What equation is used for calculating the pH of an acid buffer ?
Answer:
Hendersen’s equation is used to calculate the PH of an acid buffer
PH = PKa + log \(\frac{\text { [Salt] }}{[\text { Acid] }}\)
![]()
Question 37.
Phosphoric acid (H3PO4) have three ionization constants Ka1, Ka2 and Ka3. Among these ionization constants which has a lower value ? Give reason for it ? Answer:
Phosphoric acid (H3PO4) has
Ka1 – 7.5 × 10-3
Ka2 – 6.2 × 10-8
Ka3 – 4.2 × 10-13
Ka3 has lower value.
Reason :
- It is more difficult to remove a proton from the negativeion due to electro static forces.
- It is difficult to remove a proton from \(\mathrm{HPO}_4^{-2}\) anion.
Question 38.
Ice melts slowly at high altitudes. Explain. Why ?
Answer:
Ice melts slowly at high altitudes
Reason :
- Ice and water are equilibrium only at a particular temperature and pressure conditions.
- At high attitude temp and pressure conditions are changed.
Short Answer Questions
Qeustion 1.
Write expression for the equilibrium constant, Kc for each of the following reactions.
(i) 2NOCl(g) ⇌ 2NO(g) + Cl2(g)
(ii) 2Cu(NO3)2(s) ⇌ 2CUO(s) + 4NO2(g) + O2(g)
(iii) CH3COOC2H5(aq) + H2O(l) ⇌ CH3COOH(aq) + C2H5OH(aq)
(iv) Fe+3(aq) + 3OH–(aq) ⇌ Fe(OH)3(s)
Answer:
i) Given equation
2NOCl(g) ⇌ 2NO(g) + Cl2(g)
Equilibrium constant Kc = \(\frac{\left[\mathrm{NO}^2\left[\mathrm{Cl}_2\right]\right.}{[\mathrm{NoCl}]}\)
ii) Given equation
2Cu(NO3)2(s) ⇌ 2CUO(s) + 4NO2(g) + O2
Kc = (NO2)4 (O2)
iii) CH3COOC2H5(aq) + H2O(l) ⇌ CH3COOH(aq) + C2H5OH(aq)
Kc = \(\frac{\left[\mathrm{CH}_3 \mathrm{COOH}\right]\left[\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}\right]}{\left[\mathrm{CH}_3 \mathrm{COO} \mathrm{C}_2 \mathrm{H}_5\right]}\)
iv) Fe+3(aq) + 3OH–(aq) ⇌ Fe(OH)3(s)
Kc = \(\frac{1}{\left[\mathrm{Fe}^{+3}\right]\left[\mathrm{OH}^{-}\right]^3}\)
![]()
Question 2.
Derive the relation between Kp and Kc for the equilibrium reaction
N2(g) + 3H2(g) ⇌ 2NH3(g) [Mar. 13]
Answer:
Given equation (Equilibrium reaction)
N2(g) + 3H2(g) ⇌ 2NH3(g)
We can make the following generalisation concerning the composition of equilibrium mixtures : If Kc > 103 products predominate over reactants, i.e., if Kc is very large, the reaction proceeds nearly to completion. Consider the following examples :
a) The reaction of H2 with O2 at 500 K has a very large equilibrium constant Kc = 2.4 × 1047
b) H2(g) + Cl2(g) ⇌ 2Hl(g) at 300 K has Kc = 4.0 × 1031
c) H2(g) + Br2(g) ⇌ 2HBr(g) at 300 K. Kc = 5.4 × 1018
If Kc < 10-3 reactants predominate over products i.e, if Kc is very small the reaction proceeds rarely.
Consider the following examples :
a) The decomposition of H2O into H2 and O2 at 500 K has a very small equilibrium constant.
Kc = 4.1 × 10-48
b) N2(g) + O2(g) ⇌ 2NO(g)
at 298 K has Kc = 4.8 × 10-31
If Kc is in the range of 10-3 to 103 appreciable concentrations of both reactants and products are present. Consider the following examples :
a) For reaction of H2 with I2 to give HI.
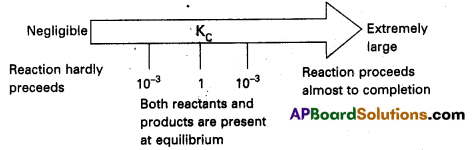
b) Also, gas phase decomposition of N2O4 to NO2 is another reaction with a value of Kc = 4.64 × 10-3 at 25°C which is neither too small nor too large. Hence equilibrium mixtures contain appreciable concentrations of both N2O4 and NO2.
These generarlisations are illustrated.
Question 3.
State law of chemical equilibrium ? What is Kc for the following equilibrium when the equilibrium concentration of each substance is [SO2] = 0.60 M,
[O2] = 0.82 M and [SO3] = 1.90 M
2SO2(g) + O2(g) ⇌ 2SO3(g)
Answer:
The ratio of product of molar concentrations of the products to the product of molar concentrations of the reactants has a constrant value. This is known as the equilibrium law (or) law of chemical equilibrium.
Given equation is
2SO2(g) + O2(g) ⇌ 2SO3(g)
Given [SO2] = 0.60M, [O2] = 0.82M, [SO3] – 1.90 M
Kc = \(\frac{\left[\mathrm{SO}_3\right]^2}{\left[\mathrm{SO}_2\right]^2\left[\mathrm{O}_2\right]}=\frac{(1.9)^2}{(0.6)^2(0.82)}\)
= \(\frac{3.61}{0.36 \times 0.86}=\frac{3.61}{0.2952}\)
= 12.22
![]()
Question 4.
Why sealed soda water bottle on opening shows the evolution of gas with effervescence ?
Answer:
- Sealed soda bottle on opening shows evolution of gas with effervescence
- This is due to difference in solubility of CO2 at different pressures there is equilibrium between molecules of gaseous state and molecules of dissolved in the liquid state.
CO2(g) ⇌ O2 (Jusolutcoiny)
Question 5.
Explain the significance of
a) a very large value of K,
b) a very small value of K and
c) a value of K of about 1.0
Answer:
a) A very large value of K indicates reaction proceeds almost to complete.
b) A very small value of K indicates reaction hardly proceeds.
c) A value of K about 1.0 indicates that reactants and products are at equilibrium.
Qeustion 6.
Why is it useful to compare Q with K ? What is the situation when
(a) Q = K
(b) Q < K (c) Q > K
Answer:
Q and K are compared to predict the direction of reaction
a) Q = K indicates that the reaction mixture is already at equilibrium
b) Q < K indicates that the reaction proceeds in the direction. c) Q > K indicates that the reaction proceeds in the direction of reactants (Reverse reaction)
Qeustion 7.
For the reaction Cl2(g) + F2(g) 2Cl F (g), Kc = 19.9
What will happen in a mixture originally containing [Cl2] = 0.4 mol L–; [F2] = 0.2 mol L-1 and [Cl F] = 7.3 mol L–?
Answer:
Given reaction
Cl2(g) + F2(g) ⇌ 2ClF(g), Kc = 19.9
Given [Cl2] = 0.4 mole/lit, [F2] = 0.2 mole/lit
[ClF] = 7.3 moles/lit
∴ \(\frac{[\mathrm{ClF}]^2}{\left[\mathrm{Cl}_2\right]\left[\mathrm{F}_2\right]}=\frac{[7.3]^2}{0.4 \times 0.2}=\frac{53.29}{0.8}\) = 66.6125
Qc > Kc
∴ The reaction proceeds in the backward direction (Reactants side, Reverse Reaction)
![]()
Question 8.
Predict which of the following reaction will have appreciable concentration of reactants and products :
a) Cl2(g) 2Cl (g), Kc = 5 × 10-39
b) Cl2(g) + 2NO(g) ⇌ 2NOG (g), Kc = 3.7 × 108
c) Cl2(g) + 2NO2 (g) ⇌ 2N02a(g) Kc = 1.8
Answer:
a) Cl2(g) ⇌ 2ClF(g) Kc = 5 × 10-39
b) Cl2(g) +2NO(g) ⇌ 2NOCl(g) Kc = 3.7 × 108
c) Cl2(g) + 2 NO2(g) ⇌ 2NO2Cl(g) Kc = 1.8
- This equation (c) have appreciable concentrations of reactants and products.
- ‘Kc‘ value is neither too small nor too large. Hence equilibrium mixtures contain appreciable concentrations of reactants and products.
Question 9.
How to recognise the conditions under which changes in pressure would effect system in equilibrium.
Answer:
Effect of pressure charge : A pressure change obtained by changing the volume can affect the yield of products in case of a gaseous reaction where the total number of moles of gaseous reactants and total number of moles of ga seous products are different. In applying Le Chatelier’s principle to a heterogeneous equilibrium the effect of pressure changes on solids and liquids can be ignored because the volume (and concentration) of a solution/liquid is nearly independent of pressure.
Consider the reaction.
CO(g) + 3H2(g) ⇌ CH4(g) + H2O(g)
Here, 4 mol of gaseous reactants (CO + 3H2) become 2 mol of gaseous products (CH4 + H2O). Suppose equilibrium mixture (for above reaction) kept in a cylinder fitted with a piston at constant temperature is compressed to one half of its original volume. Then, total pressure will be doubled (according to pV = constant). The partial pressure and therefore, concentration of reactants and products have changed and the mixture is no longer at equilibrium. The direction in which the reaction goes to re-establish equilibrium can be predicted by applying the Le Chatelier’s principle.
Since pressure is doubled, the equilibrium now shifts in the forward direction, a direction in which the number of moles of the gas or pressure decreases (we know pressure is proportional to moles of the gas). The can also be understood by using reaction quotient, Qc. Let [CO], [H2], [CH4] and [H2O] be the molar concentrations at equilibrium for methanation reaction. When volume of the reaction mixture is halved, the partial pressure and the concentration are doubled. We obtain the reaction quotient by replacing each equilibrium concentration by double its value.
QC = \(\frac{\left[\mathrm{CH}_{4(\mathrm{~g})}\right]\left[\mathrm{H}_2 \mathrm{O}_{(\mathrm{g})}\right]}{\left[\mathrm{CO}_{(\mathrm{g})}\right]\left[\mathrm{H}_{2_{(\mathrm{g})}}\right]^3}\)
As QC < KC, the reaction proceeds in the forward direction.
In reaction C(s) + CO2(g) ⇌ 2CO(g), when pressure is increased, the reaction goes in the reverse direction because the number of moles of gas increases in the forward direction.
![]()
Question 10.
What property of a reaction can be used to predict the effect of a change in temperature on the magnitude of an equilibrium constant ?
Answer:
- Change in temperature leads to the charge in the value of equilibrium constant (Kc)
- The temperature dependence of the equilibrium constant depends on the sign of ∆H for the reaction.
- The equilibrium constant for an exothermic reactions (∆H = -ve) decreases as the temperature increases.
- The equilibrium constant for an endothermic reaction (∆H = +ve) increases as the temperature increases.
- Temp changes affect the equilibrium constant and rates of reactions.
Question 11.
Does the number of moles of reaction products increase, decrease or remains same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume ?
i) PCl5(g) ⇌ PCl3 (g) + Cl2 (g)
ii) CaO(s) + CO3(g) ⇌ CaCO3 (s)
Answer:
i) PCl5(g) ⇌ PCl3(g) + Cl2(g)
Decrease in pressure by increasing volume leads to the reaction goes in forward direction be cause no. of moles of gas decrease in the forward direction.
∴ No. of moles of reaction products decreases.
ii) CaO(s) + CO2(g) ⇌ CaCO3(s)
Decrease in pressure by increasing volume the reaction does not move in any direction because only one gaseous product present i.e. CO2(g). So nochange in no. of moles of reaction products.
Question 12.
Which of the following reactions will get affected by increasing the pressure ? Also mention whether change will cause the reaction to go into forward or back ward direction.
i) COCl2(g) ⇌ CO(g) + Cl2 (g)
ii) CH4(g) + 2S2(g) ⇌ CS2 (g) + 2H2S(g)
iii) CO2(g) + C(s) ⇌ 2CO(g)
iv) 4NH3(g) + 5O2(g) ⇌ 4NO(g) + 6H2O(g)
Answer:
i) COCl2(g) ⇌ CO(g) + Cl2(g) (affected by pressaure)
Increase in pressure the reaction goes in reverse direction and No. of moles of gas increase in the forward direction. .
ii) CH4(g) + 2S2(g) ⇌ CS2(g) + 2H2(s)
No. of reactants and No. of products are same, pressure has no affect.
iii) CO2(g) + C(s) ⇌ 2 CO(g) (affected by pressure)
iv) 4NH3(g) + 5O2(g) ⇌ 4 NO(g) + 6H2O(g) (affected by pressure)
Increase in pressure, the reaction goes in reverse direction and No. of moles of gas increase in the forward direction.
![]()
Question 13.
How will an increase in pressure affect each of the following equilibria ? An increase in temperature ?
i) 2NH3(g) ⇌ N2(g) + 3H2(g) ∆ H = 92 kJ
ii) N2(g) + O2(g) ⇌ 2NO(g) ∆ H = 181 kJ
iii) 2O3(g) ⇌ 3O2(g) ∆ H = – 285 kJ
iv) CaO(S) + CO2(g) ⇌ CaCO2(s) ∆ H = – 176 kJ
Answer:
i) 2NH3(g) ⇌ N2 + 3H2(g) ∆H = +92KJ
- Increase in pressure favours backword reaction
- Increase in temperatures favours to shift the equilibrium right.
ii) N2(g) + O2(s) ⇌ 2NO(s) ∆H = 181 KJ
- Pressure has no effect. NP = NR
- Increase in temperature favour to shift the equilibrium right
jjj) 2O3(g) 3O2(g) ⇌ ∆H = -285 KJ .
- Increase in pressure favours backward reaction
- Increase in temperative favours to shift the equilibrium left
iv) CaO(s) + CO2(g) ⇌ CaCO3(s) ∆H = -176 KJ
- Pressure has no effect.
- Increase in temperature favour to shieft the equilibrium left.
Question 14.
The dissociation of HI is independent of pressure, while the dissociation of PCl5 depends upon the pressure applied explain.
Answer:
Dissociation of HI
2HI(g) ⇌ H2(g) + I2(g)
Here np = nR
∴ Pressure has no effect on the above reaction.
Dissociation of PCl5
PCl5(g) ⇌ PCl3(g) + Cl2(g)
Here np ≠ nR
∴ This reaction has affected by pressure
Question 15.
Explain the terms :
- electrolyte
- Non-electrolyte
- strong and weak electrolytes
- ionic equilibrium
Answer:
- Electrolyte: The substances either in molten state (or) in solution conducts electricity and at the same time undergoes chemical decomposition, e.g.: HCl, HNO3 etc.
- Non-electrolytes: The substances which donot ionise (or) chemical decomposed when dis-solved in a solvent.
e.g.: Sugar, urea etc. - Strong Electrolytes: The electrolytes which readily under go chemical decomposition are called strong electrolytes.
eg.: NaOH, HG, H2SO4 etc.,
Weak electrolystes : The electrolytes which donot readtions undergo chemical decomposition are called weak electrolytes.
eg. : CH3COOH, NH4OH etc., - Ionic equilibrium is a state of equilibrium set up between ionised and unionised molecule. In weak electrolytes, equilibrium is established between ions and the unionized molecules. This type of equilibrium involving ions in aq. solution is called ionic equilibrium.
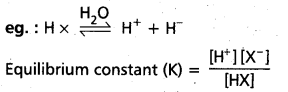
![]()
Question 16.
Explain the terms :
i) extent of ionization and on what factors it depends
ii) dissociation
iii) ionization
Answer:
Acids are generally represented as ‘HX’ and bases are represented as ‘BOH’.
Ionization of acids and bases : HX ![]() H+ + X–
H+ + X–
BOH ![]() B+ + OH–
B+ + OH–
This process of splitting of acids and bases when dissolved in water is called ‘ionization’ or ‘dissociation1. The extent of ionization of acids and bases depends on the polarity of the molecule. For strong acids and strong bases extent of ionization is large. The extent of ionization is less for weak acids or bases.
This extent of ionization depends on the concentration of the solution of the substance. Process of ionization is an equilibrium process.
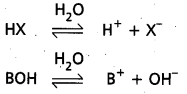
Hence, the equilibrium constants are expressed as Ka = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{X}^{-}\right]}{[\mathrm{HX}]}\)
Ka = acid ionization constant (or) acid dissociation constant.
Kb = \(\frac{\left[\mathrm{B}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{BOH}]}\)
Kb = base ionization constant (or) base dissociation constant.
Question 17.
Explain the Arrhenins concept of acids and bases.
Answer:
According to Arrhenius
Acid : Acids are the substances that dissociates in water to gave H+ ions.
e.g. : HCl, H2SO4 etc..
H x(aq) → H+(aq) + x–(aq)
Base : Bases are the substances that produce hydrorylions (OH–) ion dissociation in water
e.g. : NaOH, KOH MOH,
MOH(aq) → M+(aq) + OH–(aq)
![]()
Question 18.
What is a, conjugate acid – base pair ? Illustrate with examples. [A.P. Mar. 16]
Answer:
Conjugate acid – base pair:
A pair of a Bronsted acid and a base that differs by one proton (H+) is known as conjugate acid – base pair.
Consider the following reaction :
CH3COOH + H2O ⇌ H3O⊕ + CH3COO⊖
It involves two conjugate pairs. The acid – base pairs are :

Question 19.
Acetic acid is a weak acid. List, in order of descending concentration, all of the ionic and molecular species present in 1 M aqueous solution of acetic acid.
Answer:
[H2O] > [CH3COOH] > [H3O+] [CH3COO–] > [OH–]
Question 20.
Show by suitable equations that each of the following species can act as a Brostead acid.
a) H3O+
b) HCl
c) NH3
d) HSO4–
Answer:
a) H3O+ → H2O + H+
Proton donar Hence a Bronsted acid
b) HCl → H+ + Cl–
Proton donar Hence a Bronsted acid
c) NH3 is bronsted base it’s not an acid
(Sometimes NH3 → NH–2 + H+ as acid]
d) HSO4– → H+ + SO4-2
proton donar Hence Bronsted acid.
Question 21.
Show by suitable equations that each of the following spices can act as a Bronsted base.
a) H3O
b) OH–
c) C2H5OH
d) HPO4-2
Answer:
a) H2O + H+ → H3O+
Proton acceptor Hence a Bronsted base
b) OH– + H+ → H2O
Proton acceptor Hence a Bronsted base
c) C2H5OH is a proton donar
So it is not a bronsted base it is acid
d) HPO4-2 + H+ → H2PO4–
proton acceptor Hence it is Bronsted base.
![]()
Question 22.
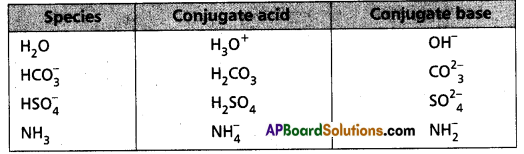
The species H2O, HCO4–, HSO4– and NH3 can act both as Bronsted acids and bases. Give the corresponding conjugate acid and base for each of them.
Answer:
The answer is given in the following Table :
Question 23.
Write equation that shows H2PO4– acting both as an acid and as a base.
Answer:
As an acid :
H2Po4– → H+ + HP2PO4-2
Proton donar
As a base:
H2Po4– + H+ → H3PO4
Proton acceptor
Question 24.
Write the conjugate acid and conjugate base of each of the following :
a) OH–
b) H2O
c) HCO3–
d) H2O2
Answer:

![]()
Question 25.
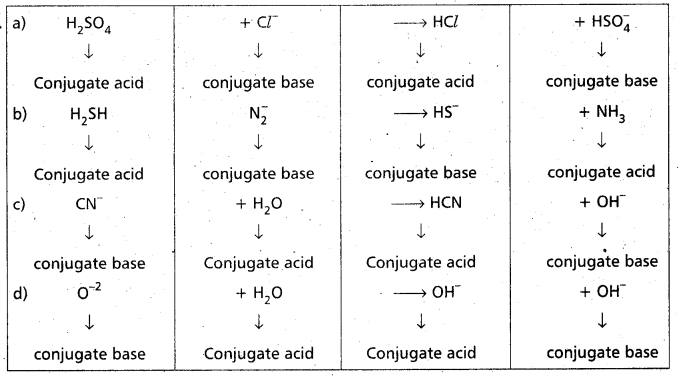
Identity and label the Bronstead acid and its conjugate base, the Bronsted base and its conjugate acid in each of the following equations.
a) H2SO4 + Cl– → HCl + HSO4–
b) H2S + NH2 → HS– + NH3
c) CN– + H2O → HCN + OH–
d) O-2 + H2O → 2OH–
Answer:
Question 26.
Classify the species AlCl3, NH3, Mg+2 and H2O into Lewis acids and Lewis bases and justify your answer ?
Answer:
- AlCl3, Mg+2 are lewis acids because These are electron pair acceptory
- NH3, H2O are lewis bases becuse. These are electron pair donors.
Question 27.
What are the strengths of conjugate bases of a strong acid and a weak acid ?
Answer:
A strong acid has a weak conjugate base
Eg : HCl, Cl–
A weak acid has a strong conjugate base
Eg : CH3COOH, CH3COO–
Question 28.
What are the strength of conjugates acids of a strong base and weak base ?
Answer:
Strong base has a weak conjugate acid
Eg : HS–, H2S
A weak base has a stong conjugatge acid
Eg : ClO–4, HClO4
Question 29.
Define ionic product of water. What is its value at room temperature ?
Answer:
At a given temp, the product of the concentrations of H+ and OH– ions in water is called ionic product
Ionic product Kw = [H–] [OH–]
At 25°C Kw = 1.008 × 10-14 mole2/lit2
At 25°C Ionic product of water Kw = 1.008 × 10-14 mole2/lit2
Units: mole2/lit2
![]()
Question 30.
Define pH. pH cannot be calculated directly from the molar concentration of a weak acid or weak base. Why ? Derive an equation for the pH of a weak acid.
Answer:
The negative logarithm on value to the 10 of the hydrogen ion concentration expressed in moles/lit, in a solution is know as pH. of the solution.
pH : – log (H+) = – log10 \(\frac{1}{\left(\mathrm{H}^{+}\right)}\)
In case of a weak acid (or) weak base extent of ionisation is low so pH cannot be calculated directly from their molar concentrations.
Derivation of pH of a weak acid :
A general step wise approch can be adopted to evaluate the pH of the weak acid as follows.
Step 1. The species present before dissociation are identified as Bronsted – Lowry acids/ bases.
Step 2. Balanced equations for all possibel reactions i.e., with a species acting both as acid as well as base are written.
Step 3. The reaction with the higher Ka is identified as the primary reaction whilst the other is a subsidiary reaction.
Step 4. Enlist in a tabular form the following values for each of the species in the primary reaction.
a) Initial concentration. C.
b) Change in concentration on proceeding to equilibrium in terms of a, degree of ionization.
Step 5. Substitute equilibrium concentrations into equilibrium constrant equation for principal reaction and solve for α.
Step 6. Calculate the concentration of species in principal raction.
Step 7. Calculate pH = – log [H3O+]
The above mentioned methodology has been elucidated in the following examples.
Question 31.
Write equations to show the step wise ionization of the polyprotic acids H2SO4 and H2PO4.
Answer:
Step wise Ionisation H2SO4

Question 32.
Explain how acid strength changes among
- the hydrides of the group elements and
- the hydrides in the same row of the periodic table.
Answer:
- The hydrides of the group elements acid strength decreases from top to bottom.
- The hydrides in the same row of Periodic table i.e., in a period the acid strength increases from left to right.
![]()
Question 33.
Justify the statement that water behaves like an acid and also like base on the basis of protonic concept.
Answer:
- Water has the ability to acts as an acid and as well as a base i.e., it behaves as an amphoteric substance.
- The following are the supporting reactions for the fact that water behaves as an amphoteric substance.
- As an acid :
H2O(l) + NH3(aq) ⇌ OH–(aq) + NH4+(aq)
H2O is proton do nor i.e., an acid according to Bronsted sense - As a base:
H2O(l) + H2S(aq) ⇌ H3O+(aq) + HS–(aq)
H2O is proton acceptor i.e., a base according to Bronsted Sense
Question 34.
What is common ion effect ? Illustrate.
Answer:
Common ion effect : The decrease in the ionisation (dissociation) of a weak electrolyte, by the addition of a strong electrolyte having an ion common with the weak electrolyte, is known as common ion effect.
Example : The dissociation of NH4OH is diminished by the addition of NH4Cl due to the common ion, NH4+ ion
NH4OH ⇌ NH4⊕ + OH⊖
NH4OH ![]() NH4+ + OH⊖ (addition of NH4Cl)
NH4+ + OH⊖ (addition of NH4Cl)
Importance of this effect In qualitative analysis :
- This principle is used in the systematic qualitative analysis of cations.
- The concentration of S2- in II group or OH– ion in III group of chemical analysis is controlled by HCl and NH4OH on the basis of common ion effect.
H+ ion is common to H2S (II group)
NH4+ ion is common to NH4OH (IV group) . - The common ion effect principle is also used in controlling the H+ ion concentration in buffer solutions.
- It is also used in the purification of common salts by passing dry HCl gas into impure salt solution.
![]()
Question 35.
Define solubility product ? Write solubility product expressions for the following :
(i) Ag2Cr2O7
ii) Zr3(PO4)4
Answer:
Solubility product (KSP) : The product of the concentrations of the cation and the anion in a saturated solution of a salt at room temperature is called solubility product (Ksp).
Ksp = [Mn+][An-]
Significance of solubility product in chemical analysis : In any solution of a salt, if the product of [Mn+] and [An-] is greater than the solubility product (KSP) of the salt, then only the salt gets precipitated. For example,
i) If the product of [Cu 2+] & [S-2] in the II group (in presence of acid) of chemical analysis exceeds the value of KSP of CuS, then only CuS will be precipitated in the group. Similar argument applies to other metal ions in the group namely (Cd2+, Bi3+, Hg2+, Sb2+, etc).
ii) If the product of [Zn2+] and [S2-] in ammonical medium in IV group of chemical analysis exceeds the value of KSP of ZnS, it will be precipitated. Similar arguments apply to Mn2+, Ni2+ etc.
a) Solubility product expression for Ag2Cr2O7

Question 36.
Give the classification of salts. What type of salts undergo hydrolysis ?
Answer:
The following are the types of salts : –
- Salts of a strong acid and a strong base. Ex : NaCl
- Salts of a strong acid and a weak base. Ex : NH4Cl
- Salts of a weak acid and a strong base. Ex : CH3COONa
- Salts of a weak acid and a weak base. Ex : CH3COONH4
Types 2, 3, 4 under go hydrolysis reactions.
Question 37.
What must be true of the value of ∆G° for a reaction if
a) K > 1
b) K = 1
c) K < 1
Answer:
a) If K > 1 then ∆ G° < 0
b) If K = 1 then ∆ G° = 0
c) If K < 1 then ∆ G° > 0
![]()
Question 38.
Aqueous solution of NH4Cl is acidic. Explain.
Answer:
Given salt NH4Cl is obtained by the reaction of strong acid (HCl) and weak base (NH4OH).
The ionisation of NH4Cl as follows
\(\mathrm{NH}_4^{+}\) + Cl– ⇌ NH4Cl
The above salt under goes cationic hydrolysis
\(\mathrm{NH}_4^{+}\) + H2O ⇌ NH4OH + H+
∴ The equation solution of salt is acidic due to greater H+ ion concentration than OH– ion concentration.
∴ PH < 7
Question 39.
Aqueous solution of CH3COONa is basic explain.
Answer:
Given salt CH3COONa is obtained by the reaction of weak acid (CH3COOH) and strong base (NaOH).
The ionisation CH3COONa as follows
CH3COONa ⇌ CH3COO– + Na+
The above salt under go anionic hydrolysis
CH3COO– + H2O ⇌ CH3COOH + OH–
∴ The equation solution of salt is basic due to greater OH– ion concentration than H+ ion concentration.
∴ PH > 7
Question 40.
Give reason that acetic acid is less acidic in sodium acetate solution than in sodium chloride solution.
Answer:
Acetic acid in sodium acetate solution is less acidic.
Reasons:
- Because of common ion effect ionisation process is decreased.
- Sodium acetate is obtained by the reaction of weak acid and strong base:
Acetic acid in NaG solution is more acidic.
Here no common ion effect observed.
NaCl is the salt obtained by strong acid and strong base.
Question 41.
AgCl is less soluble in AgNO3 solution than in pure water explain.
Answer:
- AgCl is less soluble in AgNO3 because of common ion effect solubility is decreased.
- AgCl is more soluble in pure water because common ion effect not observed here.
![]()
Question 42.
Predict whether the following reaction will proceed from left to right to any measurable extent:
CH3COOH (aq) + Cl–(aq) →
Answer:
Given CH3COOH(aq) + \(\mathrm{Cl}_{(\mathrm{aq})}^{-}\) →
The reaction does not proceed from left to right because Cl– ion is obtained from strong acid do not under go hydrolysis and CH3COOH has low extent of ionisation.
Question 43.
Aqueous solution of H2S contains H2S, HS–, S-2, H3O+, OH– and H2O in varying concentrations. Which of these species can act only as a base ? Which can act only as an acid ? Which can act both an acid and as a base ?
Answer:
- H23S, H3O+ acts as only acids
- HS–, OH–, H2O acts as acids as well as bases
- S-2 acts as only base
Long Answer Questions
Question 1.
What are equilibrium processes ? Explain equilibrium in Physical and Chemical pro-cesses with examples.
Answer:
Equilibrium State (or) Equilibrium Process : The state at which the velocity of forward reaction becomes equal to the velocity of backward reaction or reverse reaction is called ‘equilibrium state’. Consider a reversible reaction.
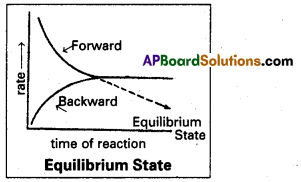
A + B ⇌ C + D taking place in a closed vessel. At the beginning we have only the reactants A and B. Their concentrations are maximum. As the reaction proceeds the reactants A and B change into the products C and D. The concentrations of the products increase gradually.
The rate of forward reaction diminishes while the reverse reaction sets in and proceeds with increasing speed. A state is soon reached where the speeds of forward and backward reactions become equal. If the rate of forward reaction Vf = The rate of reverse reaction (Vb).
The system is said to have attained a state of equilibrium. Once equilibrium is reached there is no further change in the composition of the system. The system appears to be stand still although it is dynamic. The products are formed by forward reaction just as fast as they change back into reactants by the reverse reaction.
The state at which the rate of forward reaction is equal to the rate of the reverse reaction in a reversible reaction is known as the equilibrium state or chemical equilibrium.
Examples :
i) Equilibrium physical processes :
a) Equilibrium between two phases (i.e.,) physical transformation processes.
Solid ⇌ Liquid (melting or fusion)
Solid ⇌ Vapour (sublimation)
b) Equilibrium between two different allotropic forms of same substance
α – Sulphur ⇌ β – Sulphur
ii) Equilibrium chemical processes :
a) N2 (g) + 3H2 (g) ⇌ 2NH3 (g)
b) 2SO2 (g) + O2 (g) ⇌ 2SO3 (g)
c) H2(g) + I2(g) ⇌ 2HI(g)
![]()
Question 2.
What is meant by dynamic equilibrium ? Explain with suitable examples.
Answer:
Dynamic equilibrium : The forward and reverse reactions of a reversible reaction continue to take place with equal rates simultaneously at the equilibrium stage also. Hence the equilibrium is called Dynamic equilibrium.
Explanation : In order to understand the dynamic nature of the reaction, synthesis of ammonia is carried with exactly the same starting conditions but using D2 (deuterium) in place of H2. The reaction mixtures starting either with H2 or D2 reach equilibrium with the same composition, except that D2 and ND3 are present instead of H2 and NH3. After equilibrium is attained, these two mixtures (H2, N2, NH3 and D2, N2, ND3) are mixed together and left for a while. Later when this mixture analysed, it is found that the concentration of ammonia is just the same as before.
However, when this mixture is analysed by a moss spectrometer, it is found that ammonia and all deuterium containing forms of ammonia (NH3, NH2D, NHD2 and ND3) and dihydrogen and its deutrated forms (H2, HD and D2) are present. Thus one can conclude that scrambling of H and D atoms in the molecules must result from a continuation of the forward and reverse reactions in the mixture. If the reaction had simply stopped when they reached equilibrium, then there would have been no mixing of isotopes in this way.
Use of isotope (deuterium) in the formation of ammonia clearly indicates that chemical reaction react a state of dynamic equilibrium in which the rates of forward and reverse reactions are equal and there is no net change in composition.
Question 3.
Give the General characteristics of equilibria involving physical processes ?
Answer:
Characteristics of general equilibria :
- The rate of the forward reaction is equal to the rate of the reverse reaction (uf = ub).
- The concentrations of the reactants and the products remain unchanged with time.
- The observable properties such as pressure, concentration, density, colour also remain unchanged with time.
- The equilibrium is dynamic in nature. Both the forward reaction and the reverse reaction continue to take place simultaneously with equal rates.
- A catalyst does not alter the state of equilibrium or the composition of the chemical substances of the reaction at the equilibrium. It only speeds up the attainment of the equilibrium.
- Chemical equilibrium can be established from either side of the reversible reaction.
![]()
Question 4.
What are the important features of equilibrium constant ? Discuss any two applications of equilibrium constant.
Answer:
The ratio of product of molar concentrations of products to the product of molar concentrations of reactants is called equilibrium constant (Kc)
Ex : aA + bB ⇌ cC + dD
KC = \(\frac{[C]^c[D]^d}{[A]^a[B]^b}\)
KC for reverse reaction is the inverse of the KC for the reaction in the forward direction.
Concentration equilibrium constant (KC) and pressure equilibrium constant (Kp) are related as follows
Kp = KC(RT)∆n
∆n = np – nR
While writing KC expression pure liquids, pure solids concentration are ignored Applications :
a) In predicting the extent of reaction :
The numerical value of the equilibrium constant for a reaction indicates the extent of the reac-tion. But it is important to note that an equilibrium constant does not give any information about the rate at which the equilibrium is reached the Magnitude of ke or Kp is directly proportional to the concentrations of products (as these appear in the numerator of equilibrium constant expression) and inversely proportional to the concentrations of the reactants (these appear in the denominator). This implies that a high value of K is suggestive of a high concentration of products and vice- versa.
We can make the following generalisation concerning the composition of equilibrium mixtures : If Kc > 103 products predominate over reactants, i.e., if Kc is very large, the reaction proceeds nearly to completion. Consider the following examples :
a) The reaction of H2 with O2 at 500 K has a very large equilibrium constant Kc = 2.4 × 1047
b) H2(g) + Cl2(g) ⇌ 2HCl(g) at 300 K has Kc = 4.0 × 1031
c) H2(g) + Br2(g) ⇌ 2HBr(g) at 300 K. Kc = 5.4 × 1018
If Kc = < 10-3 reactants predominate over products i.e, if Kc is very small the reaction proceeds rarely. Consider the following examples : –
a) The decomposition of H2O into H2 and O2 at 500 K has a very small equilibrium constant.
Kc = 4.1 × 10-48
b) N2(g) + O2(g) ⇌ 2NO(g)
at 298 K has Kc = 4.8 × 10-31
If Kc is in the range of 10-3 to 103 appreciable concentrations of both reactants and products are present. Consider the following examples :
a) For reaction of H2 with I2 to give HI.

b) Also, gas phase decomposition of N2O4 to NO2 is another reaction with a value of Kc = 4.64 × 10-3 at 25°C which is neither too small nor too large. Hence equilibrium mixtures contain appreciable concentrations of both N2O4 and NO2.
These generarlisations are illustrated.
b) In predicting the direction of reaction : A and K are compared to predict the direction of reaction
a) Q = K indicates that the reaction mixture is already at equilibrium
b) Q < K indicates that the reaction proceeds in the direction. c) Q > K indicates that the reaction proceeds in the direction of reactants (Reverse reaction)
![]()
Question 5.
What is Lechatlier’s principle ? Discuss briefly the factors which can influence the equilibrium.
Answer:
Le Chatelier’s Principle – Statement: “If a system at equilibrium is subjected to the change of pressure, temperature (or) concentration, the system is shifted in such a way as to nullify the effect of change”.
Explanation:
1) Concentration: Increase of reactant concentrations pushes the equilibrium state to the products side and increase of the reactions concentrations pushes to the equilibrium to the reactants side. For example in the chemical equilibrium
H2(g) + I2(g) ⇌ 2HI(g)
Increase of H2 or I2 concentrations pushes the equilibrium in favours of HI and similarly the increase of HI concentrations pushes the equilibrium in favour of H2 and I2.
2) Pressure : Pressure will have no effect on the equilibrium reactions in which there is no change in the number of moles of the reactants and the products.
For example pressure will have no effect on
H2(g) + I2(g) ⇌ 2HI(g) equilibrium
(or) N2 (g) + O2 (g) ⇌ 2NO (g) equilibrium
But in the case of reactions in which there is a change in the number of moles of the reactants and the products increase of pressure pushes the reaction equilibrium in the direction in which there is a decrease in the number of moles.
For example in the reaction PCl5 (g) ⇌ PCl3 (g) + Cl2 (g)
Increase of pressure favours the backward reaction PCl3 (g) + Cl2(g) → PCl5 (g) and the decrease of pressure favour the forward reaction PCl5 (g) → PCl3 (g) + Cl2 (g)
3) Temperature : Increase of temperature favour the endothermic reaction and decrease of temperature favours exothermic reactions.
For example .
N2 (g) + O2 (g) ⇌ 2N0(g) – 180.8 kJ
Increase of temperature favours The forward reaction
N2 (g) + O2 (g) → 2NO (g) (since endothermic)
decrease of temperature favour the dissociation of NO into N2 and O2 since it is exothermic.
The backward reaction
2NO (g) → N2 (g) + O2 (g) (since exothermic)
Question 6.
Discuss the application of Lechaterlier’s principle for the industrial synthesis of Ammonia and sulphur trioxide.
Answer:
Applications of Le Chatelier’s principle to synthesis of Ammonia by Haber’s process :
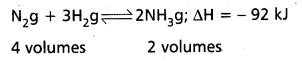
Nitrogen and Hydrogen combine to form ammonia. The formation of ammonia is reversible and exothermic reaction. It is accompanied by decrease in volume.
Effect of Pressure: 1 volume of N2 combines with 3 volumes of H2 to form 2 volumes of NH3. There is decrease in volume in the forward reaction (4 volumes to 2 volumes). According to Le Chatelier’s principle increase of pressure favours the reaction where there is decrease in volume. So higher the pressure, greater the yield of ammonia. In practice 200 atmospheres are used in the manufacture of ammonia by Haber’s process.
Low pressures favour the reverse reaction i.e., decomposition of NH3 already formed.
Effect of Temperature : The formation of ammonia (forward reaction) is exothermic reaction
N2 + 3H2 → 2 NH3; ∆H = – 92 kJ.
Low temperatures favour the forward reaction. But at low temperatures the reaction is too slow. Therefore an optimum temperature (725 K- 775 K) is chosen in Haber’s process. To speed up the reaction, a catalyst, finely divided iron is used. To increase the activity of the catalyst molybdenum or a mixture of oxides of K after Al is used as promoter.
The reverse reaction (i.e.,) decomposition of NH3 is an endothermic reaction. High temperatures favour the decomposition of NH3. Therefore high temperatures are avoided in Haber’s process. Thus the optimum conditions are
Pressure : 200 atm
Temperature : 725-775 K
Catalyst : Fe (Powered)
Promoter : Mo (or) (K2O + Al2O3)
Application of Le Chatelier’s principle to the synthesis of SO3 :
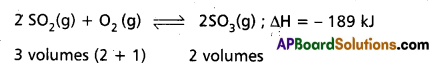
The formation of SO3 is reversible and exothermic reaction. It is accompanied by decrease in volume.
1. Effect of Pressure : 2 volumes of SO2 and one volume of O2 combine to give 2 volumes of SO3. According to Le Chatelier’s Principle increase of pressure favours the reaction where there is decrease in volume. The formation of SO3 is accompanied by decrease in volume (3 volumes to 2 volumes). Higher the pressure greater is the yield of S03. But in contact process high pressures are not used because towers used in the manufacture are corroded by the acid at these high pressures.
Low pressures favour the decomposition of SO3 as there is increase in the volume of (2 volumes to 3 volumes). Therefore optimum pressures are used (1.5 to 1.7 atmosphere).
2. Effect of Temperature : The formation of SO3 is exothermic. 189 Id of heat is evolved. High temperatures favour the reverse reaction which is endothermic and do not favour the forward reaction which is exothermic. Low temperatures are favourable for the formation of SO3. At low temperature the reaction is too slow. Therefore an optimum temperature 673 K is used. To speed up the reaction V205 is used as catalyst.
Thus the optimum conditions are
Pressure : 1.5 to 1.7 atm
Temperature : 673 K
Catalyst : V2O5 (or) Platinised asbestos
![]()
Question 7.
Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per the following endothermic reaction. .
CH4(g) + H2O(g) ⇌ CO(g) + 3H2 (g)
a) Write an expression for Kp for the above reaction.
b) How will the values of Kp and composition of equilibrium mixture be affected by
- increasing the pressure
- increasing the temperature
- using a catalyst ?
Solution:
a) Given equation
CH4(g) + H2O(g) ⇌ CO(g) + 3H2(g)
Kp = \(\frac{\mathrm{P}_{\mathrm{CO}} \times \mathrm{P}_{\mathrm{H}_2}^3}{\mathrm{P}_{\mathrm{CH}_4} \times \mathrm{P}_{\mathrm{H}_2 \mathrm{O}}}\)
b)
- Increase of pressure the reaction proceeds in reverse direction because the no. of moles of gas increases in the forward direction.
Increase pressure Kp value increases. - Increase of temperature of the reaction mixture at equilibrium favours the reaction in the direction in which heat is absorbed.
Increase of temperature Kp value increases. - A catalyst does not disturbs (or) change the chemical reaction it just speed up the attaining of equilibrium.
Question 8.
Describe the effect of :
a) addition of H2
b) addition of CH3OH
c) removal of CO
d) removal of CH3OH on the equilibrium of the reaction
2H2(g) + CO(g) ⇌ CH3OH(g)
Solution:
a) Addition of H2 (Reactant):
Increasing the concentration of reactants in the reaction mixture at equilibrium favours the forward reaction.
b) Addition of CH3OH (Product):
Increasing the concentration of products in the reaction mixture at equilibrium favours the reverse reaction.
c) Removal of CO (Reactant):
Decreasing the concentration of reactants in the reaction mixture at equilibrium favours the reverse reaction.
d) Removal of CH3OH (Product):
Decreasing the concentration of products in the reaction mixture at equilibrium favours the forward reaction.
![]()
Question 9.
At 473K, equilibrium constant Kc for the decomposition of phosphorous pentachloride, PCl5, is 8.3 × 10-3. If the decomposition is depicted as :
pCl5 (g) pCl3 (g) + Cl2 (g) ∆H = 124.0 kJ mol-1.
a) Write an expression of Kc for the reaction
b) What is the value of Kc for the reverse reaction at the same temperature ?
c) What would be effect on Kc if
(i) more PCl5 is added
(ii) pressure is increased
(iii) the temperature is increased.
Solution:
Given
PCl5(g) ⇌ PCl3(g) + Cl2(g) ∆H = 124.0 kJ/mole
KC = 8.3 × 10-3
a) KC = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
b) Given KC = 8.3 × 10-3
We have to calculate KC for reverse reaction
i.e., PCl3(g) + Cl2(g) ⇌ PCl5(g)
∴ Kc for the reverse reaction = \(\frac{1}{8.3 \times 10^{-3}}\)
= 0.12048 × 103
= 120.48
c) i) More PCl5 is added KC value is decreased.
ii) By the increase of pressure KC value is increased.
iii) Given reaction is Endothermic so increase of temperature increases KC value.
Question 10.
Explain the concept of Bronsted acids and Bronsted bases. Illustrate the answer with suitable examples.
Answer:
According to Bronsted theory o substance which can donate a proton to the other substance is known as acid. A substance which accept a proton from other substance is a base.
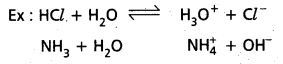
Here HCl donates a proton to water and behaves as Bronsted Lowry acid. Similarly NH3 accepts a proton from H2O and acts as Bronsted Lowry base.
Above reaction is a reversible reaction so that H3O+ can donate proton to act as acid. Cl– can accept a proton to act as base. Thus each acid base reaction equilibrium involves two acids and two bases. Each pair differs by a proton, such acid base pair is called Conjugate acid base pain.
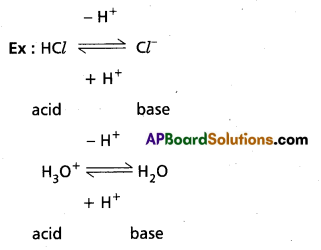
According to this theory strengths of acids and bases can be explained.
An acid which show great tendency to donate protons is a strong acid and an acid which shows less tendency to donate proton is a weak acid.
A base which shows great tendency to accept a proton is a strong base and a base which shows less tendency to accept a proton is a weak base.
![]()
Question 11.
Explain Lewis acid-base theory with suitable example. Classify the following species into Lewis acids and Lewis bases and show these act as Lewis acid / base.
a) OH–
b) F–
c) H+
d) BCl3
Answer:
Lewis theory of acids and bases : G.N. Lewis proposed a more generalised theory of acids and bases. According to this theory.
Acid : A substance that can accept an electron pair to form a co-ordinate covalent bond is called an acid.
Types of Lewis acids :
Lewis acids are of 5 types.
1) All Cations : Simple cations Ag⊕, CO+3, Cu+2, Fe+3, Al+3 can act as Lewis acids.
2) Compounds in which the central atom has an incomplete octet and possessing an empty orbital can act as Lewis acids.
Ex : BF3, BCl3, AlCl3, FeCl3.
3) Compounds in which the central atom has vacant d-orbitals and may expand its octet can act as lewis acids.
Ex : SiF4, SF4, TeF4, SnCl4, FeCl3.
4) Molecules having multiple bonds between atoms of dissimilar electronegativities can behave like Lewis acids.
Ex : CO2, SO2, SO3, NO2, Cl2O7, P4O10
5) Elements with six electrons in the valence shell or electron sextet can act as Lewis acids.
Ex : O, S
Base : According to Lewis theory a base is a substance which can donate an electron pair to form a co-ordinate covalent bond.
Types of Lewis bases : Lewis bases are divided into three types.
1) All anions
Ex: Cl⊖, OH⊖, CN⊖, \(\mathrm{NH}_2^{\ominus}\), F⊖, SCN⊖ All simple anions can act as Lewis bases.
2) Molecules with one or two lone pairs on the central atom can act as Lewis bases.
Ex : ![]()
a) Hydrenyl ion is a lewis base as it can donate an electron lone pair (:OH–).
b) Flouride ion acts as a Lewis base as it can donate any one of its four electron lone pairs.
c) A Proton is a lewis acid as it can accept alone pair of electrons from bases like hydrenyl ion and flowride ion.
d) BCl3 acts as a lewis acid as it can accept a lane pair electrons from species like ammenia or amine molecules.
![]()
Question 12.
What is degree of ionization in respect of weak acids and weak bases ? Derive the relationship between degree of ionization (α) and ionization constant (Ka) for the weak acid HX.
Answer:
Degree of ionization (α):
The extent of ionization (or) dissociation of a weak acid or weak base is termed as its Degree of ionization (α). Let the concentration of weak acid (HX) be ‘C moles/lit and the degree of ionization be ‘α’. Hence at equilibrium,
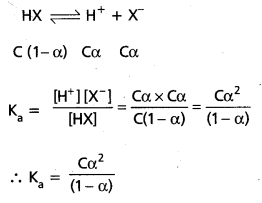
If ‘α’ is neglected compared to ‘one’ in the denominator.
We have Ka = Cα2 ⇒ α2 = \(\frac{K_a}{C} \Rightarrow \alpha=\sqrt{\frac{K_a}{C}}\)
Similar equation can be written for the ionization of weak base (BOH) in aq. solution.

Therefore strengths of two acids or two bases are compared generally by their Ka or Kb values. Higher Ka or Kb value, stronger is the acid or base.
Question 13.
Define pH. What is buffer solution ? Derive Henderson – Hasselbalch equation for calculating the pH of an acid buffer solution.
Answer:
pH : “The negative value of the logarithm to the base 10, of the hydrogen ion concentration, expressed in moles / lit, in a solution is known as the pH of the solution”.
Mathematically, pH = – log10 [H+]
Buffer Solution:
“A buffer solution is that solution which resists any change in its pH value on dilution (or) on addition of a small amount of a strong acid or a strong base
Ex : Acidic buffer: (CH3COOH + CH3COONa)
Basic buffer: (NH4OH + NH4Cl)
Preparation of buffer solutions :
1) Acid buffer solutions : An acid buffer consists of weak acid and its salt with strong base.
Ex : (CH3COOH + CH3COONa)
Acid buffer solutions are normally prepared by mixing either equal or different volumes of equimolar solutions of a weak acid and its salt.
2) Base buffer solutions : A basic buffer solution consists of a mixture of a weak base and its salt with a strong acid.
Ex : (NH4OH + NH4Cl)
Base buffer solutions are prepared generally, by mixing either equal or different volumes of equimolar solutions of a weak base and its salt.
Derivation of Hendersen’s equation for an acid buffer :
i) Consider the acid buffer HA + NaA
HA ⇌ H+ + A-
NaA ⇌ Na+ + A–
Acid dissociation constant Ka = \(\frac{\left[\mathrm{A}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)
Here due to common ion effect
Question 14.
Explain the term “Hydrolysis of salts” with examples. Discuss the pH of the following types of salt solutions.
(i) Salts of weak acid and strong base.
(ii) Salts of strong acid and weak base. [T.S. Mar. 16]
Solution:
It may be defined as a phenomenon in which the anion or cation or both of a salt react with water producing excess of OH⊖ ions or H⊕ ions or both in aq. solution”.
i) -4 Given salt CH3COONa is obtained by the reaction of weak acid (CH3COOH) and strong base (NaOH).
-4 The ionisation CH3COONa as follows
CH3COONa ⇌ CH3COO– + Na+
The above salt undergo anionic hydrolysis
CH3COO– + H2O ⇌ CH3COOH + OH–
The aq solution of salt is basic due to greater OH– ion concentration than H+ ion concentration.
∴ PH > 7
ii) -4 Given salt NH4;C3 is obtained by the reaction of strong acid (HCl) and weak base (NH4OH).
-4 The ionisation of NH4Cl as follows
\(\mathrm{NH}_4^{+}\) + Cl– ⇌ NH4Cl
-4 The above salt under goes catioric hydrolysis
\(\mathrm{NH}_4^{+}\) + H2O ⇌ NH4OH + H+
∴ The equation solution of salt is acidic due to greater H+ ion concentration than OH– ion concentration.
∴ PH < 7
![]()
Question 15.
What is solubility product ? Explain the common ion effect on solubility of ionic salts.
Solution:
Solubility product (KSP) : The product of the concentrations of the cation and the anion in a saturated solution of a salt at room temperature is called solubility product (KSP).
KSP = [Mn+][An-]
Significance of solubility product in chemical analysis :
In any solution of a salt, if the product of [Mn+] and [An-] is greater than the solubility product (KSP) of the salt, then only the salt gets precipitated. For example,
i) If the product of [Cu2+] & [S-2] in the II group (in presence of acid) of chemical analysis exceeds the value of KSP of CuS, then only CuS will be precipitated in the group. Similar argument applies to other metal ions in the group namely (Cd2+, Bi3+, Hg2+, Sb2+, etc).
ii) If the product of [Zn2+] and [S2-] in ammonical medium in IV group of chemical analysis exceeds the value of Ksp of ZnS, it will be precipitated. Similar arguments apply to Mn2+, Ni2+ etc.

- Given salt CH3COONa is obtained by the reaction of weak acid (CH3COOH) and strong base (NaOH).
- The ionisation CH3COONa as follows
CH3COONa ⇌ CH3COO– + Na+ - The above salt undergo anionic hydrolysis
CH3COO– + H2O ⇌ CH3COOH + OH–
∴ The aq solution of salt is basic due to greater OH– ion concentration than H+ ion concentration.
∴ PH > 7
Given salt NH4Cl is obtained by the reaction of strong acid (HCl) and weak base (NH4OH).
The ionisation of NH4Cl as follows
\(\mathrm{NH}_4^{+}\) + Cl– ⇌ NH4Cl
The above salt under goes catioric hydrolysis
\(\mathrm{NH}_4^{+}\) + H2O ⇌ NH4OH + H+
∴ The equation solution of salt is acidic due to greater H+ ion concentration than OH– ion concentration.
∴ PH < 7
Common ion effect on solubility of ionic salts
The common ion effect is used for almost complete precipitation of a particular ion as its sparingly soluble salt, with every low value of solubility product for gravimetric estimation. Thus we can precipitate silver ion as silver chloride, ferric ion as its hydroxide (or hydrated ferric oxide) and barium ion as its sulphate for quantitative estimations.
![]()
Question 16.
Write notes on
(i) Common ion effect.
(ii) The relation between Ksp and solubility (S) of a spaningly soluble salt BaSO4.
Solution:
i) Common ion effect : The decrease in the ionisation (dissociation) of a weak electrolyte, by the addition of a strong electrolyte having an ion common with the weak electrolyte, is known as common ion effect.
Example : The dissociation of NH4OH is diminished by the addition of NH4Cl due to the common ion, NH4+ ion
NH4OH ⇌ NH4⊕ + OH⊖
NH4OH ![]() NH4+ + OH⊖ (addition of NH4Cl)
NH4+ + OH⊖ (addition of NH4Cl)
Importance of this effect In qualitative analysis :
- This principle is used in the systematic qualitative analysis of cations.
- The concentration of S2- in II group or OH– ion in III group of chemical analysis is controlled by HCl and NH4OH on the basis of common ion effect.
H+ ion is common to H2S (II group)
NH4+ ion is common to NH4OH (IV group) . - The common ion effect principle is also used in controlling the H+ ion concentration in buffer solutions.
- It is also used in the purification of common salts by passing dry HCl gas into impure salt solution.
ii) Relation between KSP and ‘S’ of salt at BaSO4
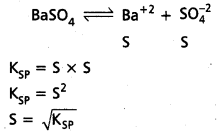
Problems
Question 1.
1 Mole of PCl5 is heated in a closed vessel of 1 litre capacity. At equilibrium 0.4 moles of chlorine is found. Calculate the equilibrium Constant.
Solutioni:
PCl5(g) ⇌ PCl3(g) + Cl2(g)
Initial [PCl5] = 1 mole/lit
At equilibrium [Cl2] = 0.4 moles/lit
[PCl3] at equilibrium = 0.4 moles/lit
[PCl5] at equilibrium = 0.6 moles/lit
KC = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
= \(\frac{0.4 \times 0.4}{0.6}=\frac{0.16}{0.6}\)
= 0.2606
Question 2.
Nitrogen dioxide forms dinitrogen tetroxide according to the equation 2 NO2 (g) ⇌ N2O4 (g) when 0.1 mole of NO2 as added to a 1 litre flask at 25°C, the concentration changes so that at equilibrium [NO2] = 0.016M and [N2O4] = 0.042 M
a. What is the value of the reaction Quotient before any reaction occurs.
b. What is the value of the equilibrium constant for the reaction.
Solution:
Given equation
2NO2(g) ⇌ N2O4(g)
a) The value of reaction quotient before any reaction occurs = 0
b) KC = \(\frac{\left[\mathrm{N}_2 \mathrm{O}_4\right]}{\left[\mathrm{NO}_2\right]^2}\)
= \(\frac{0.042}{(0.016)^2}=\frac{0.042}{0.000256}\)
= 164.06
= 1.64 × 102
![]()
Question 3.
The equilibrium constant for the reaction:
N2(g) + 3H2(g) ⇌ 2 NH3(g) at 725K is 6.0 × 10-2. At equilibrium, [H2] = 0.25 mol L-1 and [NO3] = 0.06 mol L-1. Calculate the equilibrium concentration of N2.
Solution:
Given
N2(g) + 3H2(g) ⇌ 2NH3(g)
KC = 6 × 10-2
[H2] = 0.25 moles/lit
[NH3] = 0.06 moles/lit
KC = \(\frac{\left[\mathrm{NH}_3\right]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{H}_2\right]^3}\)
6 × 10-2 = \(\frac{(0.06)^2}{\left(N_2\right)(0.25)^3}\)
[N2] = \(\frac{(0.06)^2}{6 \times 10^{-2} \times(0.25)^3}\)
= \(\frac{0.0036}{0.015625 \times 6 \times 10^{-2}}\)
= \(\frac{0.0036}{0.09375 \times 10^{-2}}\)
= 3.84 moles/lit
Question 4.
At certain temperature, Kc for the re action.
SO2 (g) + NO2 (g) ⇌ SO3 (g) + NO (g)
is 16. If intially one mole each of all the four gases are taken in one litre vessel. What are the equilibrium con centrations of NO and NO2.
Solution:
Given equations is

x = 8 – 4x
5x = 8
x = 1.6 moles/lit ∴ (NO] = 1.6 moles/lit
2 – x = 2 – 1.6 = 0.4 moles/lit
[NO2] = 0.4 moles/lit
Question 5.
Under certain conditions, the equilibrium constant for the decomposition of PCl5 (g) into PCl3 (g) and Cl2 (g) is 00211 mol L-1. What are the equilibrium concentrations of PCl5, PCl3 and Cl2, if the intial concentration of PCl5 was 1.00 M?
Solution:
PCl5(g) ⇌ PCl3 + Cl2(g)
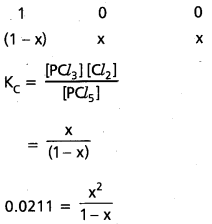
0.0211 (1 – x) = x2
0.0211 – 0.0211 x = x2
x = 0.14 M
∴ 1 – x = 1 – 0.14
= 0.86 M
∴ 1 [PCl5] = 0.86 M
∴ [PCl3] = 0.86 M
[PCl3] = [Cl2] = 0.14 M
![]()
Question 6.
For the reaction A + B ⇌ 3C at 25°C, a 3 litre vessel contains 1, 2, 4 mole of A, B and C respectively predict the direction of reaction if
a. Kc for the reaction is 10
b. Kc for the reaction is 15
c. Kc for the reaction is 10.66
Answer:
A + B ⇌ 3C at 25°C

a) Given Kc = 10
Kc< Qc
∴ Backward reaction takes place
b) Given Kc = 15
Kc > Qc
∴ Forward reaction takes place
c) Given Kc = 10.66 Q = Kc
∴ Represents equilibrium state
Question 7.
A mixture of H2, N2 and NH3 with molar concentrations 5.0 × 10-3 mol L-1, 4.0 × 10-3 mol L-1 and 2.0 × 10-3 mol L-1 respectively was prepared and heated to 500K. The value of Kc for the reaction : 3H2 (g) + N2 (g) ⇌ 2NH3 (g) at this temperature is 60. Predicts whether ammonia tends to form or decompose at this stage of concentration.
Answer:

Given Kc = 60
Kc < Qc
∴ Backward reaction i.e decomposition of NH3 takes place
Question 8.
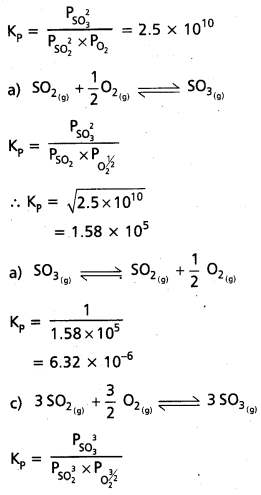
At 500 K, Kp value for the reaction
2 SO2 (g) + O2 (g) ⇌ 2SO3 (g) is 2.5 × 1010.
Find the value of Kp for each of following reactions at the same temperature.
a. SO2(g) + 1/2O2(g) ⇌ SO3 (g)
b. SO3(g) ⇌ SO2(g) + 1/2O2(g)
c. 3SO2(g) + 3/2 O2(g) ⇌ 3SO3(g)
Solution:
2SO2(g) + O2(g) ⇌ 2SO3(g)
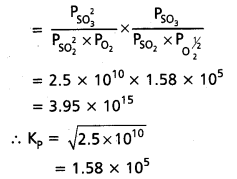
![]()
Question 9.
Kc for the reaction N2O4 (g) ⇌ 2NO2 (g) is 4.63 × 10-3 at 25°C.
a. What is the value of K at this termperature
b. At 25°C, if the partial pressure of N2O4 (g) at equilibrium is 0.2 atm1 calculate equilibrium pressure of NO2(g).
Solution:
a) Given
Na2O4(g) ⇌ 2NO2(g)
kc = 4.63 × 10-3
kp = kc (RT)∆n
= 4.63 × 10-3 × 0.0821 × 298 [∆n = 1]
= 113.27 × 10-3
= 0.1132
b) kp = \(\frac{\mathrm{P}_{\mathrm{NO}_2{ }^2}}{\mathrm{P}_{\mathrm{N}_2 \mathrm{O}_4}}\)
0.1132 = \(\frac{\mathrm{P}_{\mathrm{NO}_2{ }^2}}{0.2}\)
PNO22 = 0.2264
PNO2 = 0.15 atm
Question 10.
At 27°C, Kp value for the reversible reaction PCl5(g) PCl5(g) + Cl2(g) is 0.65, calculate Kc
Solution:
PCl5(g) ⇌ PCl3(g) +Cl2(g)
Given kp = 0.65 .
kp = k<subC (RT)∆n
0.65 = k<subC 0.082 1 × 300 [T =27°C = 300K; ∆n = 1]
k<subC = \(\frac{0.65}{24.63}\) = 0.02639
Question 11.
Kc for the reaction, N2 (g) + 3H2 (g) 2NH3(g) is 0.5 at 400K, find Kp.
Solution:
N2(g) + 3 H2(g) ⇌ 2 NH3(g)
Given kC = 0.5
T = 400 K
kp = kc (RT)∆n
kp = 0.5 × (0.0821 × 400)-2 ∆n = -2
kp = 0.5 × (8.21 × 4)-2 = 0.5 × (32.84)-2
\(\frac{0.5}{1078.46}\) = 4.63 × 10-4
Question 12.
1 mole of A and 1 mole of B are taken in a 5 litre flask, 0.5 mole of C is formed in the equilibrium of
A + B ⇌ C + D.
What is molar concentration of each species if the reaction is carried with 2 mole of A 1 mole of B in a 5 litre flask at the same temperature.
Solution:

= 0.2 – 0.133 = 0.067 M
[C] = [D] = 0.133 M
![]()
Question 13.
For the following reaction
PCl5(g) ⇌ PCl3(g) + Cl2(g) 0.4 mole of PCl5 0.2 mole of PCl3 and 0.6 mole of Cl2 are taken in a 1 litre flask. If Kc = 0.2, Predict the direction in which reaction proceeds.
Solution:
Given
PCl(g) ⇌ PCl3(g) + Cl2 (g)
QC = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
= \(\frac{0.2 \times 0.6}{0.4}\)
= 0.03
Given KC = 0.2
QC < KC
∴ Reaction proceds in forward direction.
Question 14.
In an equilibrium A + B C + D; A and B are mixed in a vessel at temperature T. The initial concentration of A was twice the initial concentration of B. After the attainment of equilibrium, concentration of C was thrice concentration of B, calculate Kc.
Solution:
Given
A + B ⇌ C + D
The initial concentrations of A was twice the initial concentration of B and after the attaining of equilibrium concentration of ‘C’ was thrice the concentration of ‘B’.
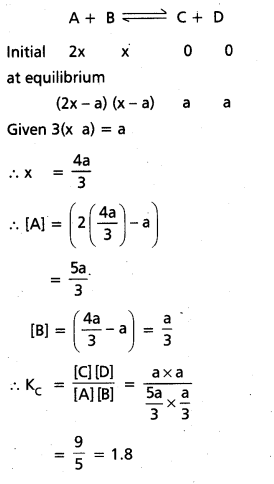
Question 15.
A mixture of SO2, SO3 and O2 gases are maintained at equilibrium in 10 litre flast at a temperature at which Kc for the reactin 2SO2(g) + O2(g) ⇌ 2SO3(g) is 100. At equilibrium.
a. If no. of moles of SO3 and SO2 inflask are same, how many moles of O2 are present.
b. If no. of moles of SO3 in flask is twice the no. of moles SO2, how many moles of O2 are present.
Solution:
a) Given
2 SO2(g) + O2(g) ⇌ 2 SO3(g)
Given KC = 100
a) Given no.of moles of SO3 = No. of moles of SO2
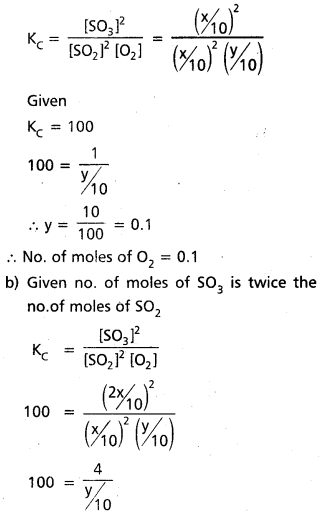
y = \(\frac{4}{10}\) = 0.4
∴ 0.4 moles of O2 present.
![]()
Question 16.
For A + B ⇌ C, the equilibrium concentrations of A and B at a temperature are 15 mol L-1. When volume is doubled the reaction has euilibrium concentration of A as 10 mol L-1. Calculate.
a) Kc
b) Concentration of C in original equilibrium
Solution:
a) Given
A + B ⇌ C + D
a) KC
b) Concentration of C in original equilibrium
a) KC = \(\frac{[\mathrm{C}]}{[\mathrm{A}][\mathrm{B}]}\)
[A] = 10 moles/lit
[B] = 10 moles/lit
[CI = 20 moles/lit
= \(\frac{20}{10 \times 10}\)
= \(\frac{20}{100}\) = 0.2
b) KC = \(\frac{[\mathrm{C}]}{[\mathrm{A}][\mathrm{B}]}\)
[AI = [B] = 15 moles/lit
0.2 = \(\frac{[C]}{15 \times 15}\)
[C] = 225 × 0.2
= 45 M
Question 17.
A vessel at 100 K contains CO2 with a pressure of 0.5 atm. Some of the CO2 is converted into CO on addition of graphite. Calculate the value of K, if total pressure at equilibnum is 0.8 atm.
Solution:

0.5 – x + 2x = 0.8
x = 0.3
∴ PCO = 0.2 atm
PCO2 = 0.6 atm
K = \(\frac{\mathrm{P}_{\mathrm{CO}_2^2}}{\mathrm{P}_{\mathrm{CO}}}\)
= \(\frac{0.36}{0.2}\) = 1.8
Question 18.
The K1, va)ue for the reaction H2(g)+ I2(g) ⇌ 2 HI(g) at 460°C is 49. If the initial pressure of H2 and I2 are 0.5 atm respectively, determine the partial pressure of each gases a equilibrium.
Solution:

x = \(\frac{3.5}{9}\)
= 0.3888
∴ PHI = 2 × 0.3888
= 0.7788 atm
PH2 = 0.5 – 0.388
= 0.111 atm
PI2 = 0.5 – 0.3888
= 0.111 atm
![]()
Question 19.
0.5 mol of H2 and 0.5 mole of I2 react in 10 litre flask at 448°C. The equilibrium constant Kc is 50 for
H2(g) + I2(g) ⇌ 2HI(g).
a) What is the value of Kp
b) Calculate mole of I2 at equilibrium.
Solution:

∴ No of moles of I2 = 0.5 – 0.3888
= 0.111 moles
Question 20.
How much PCl5 must be added to a one little vesel at 250°C in order to obtain a concentration of 0.1 mole of Cl2 at equilibrium. Kc for
PCl5(g) ⇌ PCl3(g) + Cl2(g) is 0.0414 M.
Solution:

∴ KC = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
0.0414 = \(\frac{0.1 \times 0.1}{x-0.0414}\)
0.0414 x – 0.00414 = 0.01
0.0414 x = 0.01 + 0.00414
x = 0.34154 moles
Question 21.
K for the reaction
N2(g) + 3H2(g) ⇌ 2NH3(g) at 400°C is 1.64 × 10-4.
a) Calculate Kc
b) Calculate ∆G° value using Kc value.
Solution:
Given equation N2(g) + 3H2(g) ⇌ 2NH3(g)
a) Kp = Kc (RT)∆n
∆n = 2 – (4)
= -2
1.64 × 10-4 = Kc (0.0821 × 673)-2
Kc = 1.64 × (55.2533)2 × 10-4
Kc = 0.5006
b) ∆G° = -2.303 RT log K
= -2.303 × 0.0821 × 673 × log 0.5005
= 3874 J
![]()
Question 22.
Calculate the pH of
a) 10-3 M HCl
b) 10-3 M H2SO4
c) 10-6 M HNO3
d) 0.02 M H2SO4
Solution:
a) 10-3 M HCl
pH = -log (H+)
= – log 10-3
= 3
b) 10-3 M H2SO4
pH = – log10 [H+]
= 0.001 × 2
= 0.002
pH = – log 0.002
= – log2 × 10-3
= – log2 – log 10-3
= 3 – log2
= 3 – 0.3010
= 2.699
c) 10-6 M HNO3
0.0008 M Ba(OH)2)
pOH = – log [OH–]
[OH–] = 0.0008 × 2
= 0.0016 N
∴ pOH = – log 0.0016
= – log 16 × 10-4
= – log 16 + 4 log 10
= – log24 + 4
= – 4 log 2 + 4 = 2.796
pH + pOH = 14
pH = 14 – 2.796
pH = 11.204
d) 0.02 M H2SO4
pH = -log10(H+)
[H+] = 0.02 × 2
= 0.04N
pH = – log 0.04
= -log 4 × 102
= -log4 – log 10-2
= 2 – log4
= 1.3010
![]()
Question 23.
Calculate of pH for
a) 0.001 M NaOH
b) 0.01 M Ca (OH)2
c) 0.0008 M Ba(OH)2
d) 0.004M NaOH
Solution:
a) 0.001 M NaOH
pOH = -log[OH–]
pOH = – log (0.001)
= – log 10-3
= 3
pH = 14 – pOH = 14 – 3 = 11
b) 0.01 M Ca (OH)2
pOH = -log [OH–]
[OH–] = 0.01 × 2
= 0.02 N
pOH = – log 0.02
pOH = -log 2 × 10-2
pOH = – log2 + 2 log 10
= 2 – 0.3010
= 1.699
∴ pH = 14 – pOH
= 14 – 1.699 = 12.301
c) 00008M Ba(OH)2
pOH = -log [OW]
[OH–] = 0.0008 × 2
= 0.0016N
∴ pOH = – log 0.0016
= -log 16 × 10
= -log 16 + 4log 10
= – log 24 + 4
= -4 log 2 + 4 = 2.796
pH + pOH = 14
pH = 14 – 2.796
pH = 11.204
10-6M HNO3
PH = -log [H+]
= -log 10-6
= 6 log 10
= 6
d) 0.004M NaOH
pOH = – log[OH–]
= – log 0.004
= – log 4 × 10-3
= 3 – log22
= 3 – 0.6020
= 2.398
pH = 14 – POH
= 14 – 2.398
= 11.602
Question 24.
The pH of a solution is 3.6 Calculate H3O+ ion concentration.
Solution:
pH = – log [H+]
log [H+] = – 3.6 (or) \(\overline{4} .4000\)
[H+] = anti log of \(\overline{4} .4\)
= 2.512 × 10-4.
Question 25.
The pH of a solution is 8.6 calculate the OH ion concentration.
Solution:
pH = 8.6
∴ pOH = 14 – pH
= 14 – 8.6
= 5.4
∴ pOH = – log [OH–]
log [OH–] = -5.4 (or) \(\overline{6} .6000\)
[OH–] = anti log of \(\overline{6} .6000\)
= 3.981 × 10-6
![]()
Question 26.
What is [H+] for a solution in which
a) pH = 3
b) pH = 4.75
c) pH = 4.4
Solution:
a) Given
pH = 3
∴ pH = – log [H+]
log [H+] = -3
∴ [H+] = 10-3 M
b) Given
pH = 4.75
PH = – log [H+]
log [H++] = – 4.75 (or) \(\overline{5} .2500\)
[H+] = anti log of 5.2500
= 1.77 × 10-5 M
c) Given
pH = 4.4
PH = – log [H+]
log [H+] = – 4.4 (or) \(\overline{5} .6\)
[H+] = anti log of \(\overline{5} .6\)
= 2.512 × 10-6 M
Question 27.
A solution of 0.005 M H2SO4 is diluted 100 times. Calculate the pH of diluted solution.
Solution:
0.005 M H2SO4
[H+] = 0.005 × 2 = 0.01
It is diluted to 100 times
[H+] = \(\frac{0.01}{100}\) = 0.0001
pH = – log [H+]
= – log 0.0001
= – log 10-4 = 4
![]()
Question 28.
A solution of HCl has a pH = 3. If one ml of it is diluted to 1 litre, what will be the pH of the resulting solution ?
Solution:
Given
pH = 3 for HCZ solution
∴ [H+] = 10-3 M
It is diluted to litre
∴ [H+] = \(\frac{10^{-3}}{10^3}\) = 10-6
∴ pH = – log [H+]
= – log 10-6 = 6
Question 29.
What is the pH of 10-8 M HCl ?
Solution:
The given acid solution is very dilute. Hence the H+ obtained from the acid and water must be taken into consideration.
H+ ion concentration of acid is 10-8 M
H+ ion concentration of water is 10-7 M
Total [H+] = 10-8 + 10-7
= 1.1 × 10-7 or 1.1 × 10-7 M
∴ pH = – log 1.1 × 10-7
= 7 – log 1.1 = 7 – 0.0414 = 6.995
Question 30.
Calculate the pH of the following basic solutions.
a. [OH–] = 0.05 M
b. [OH–] = 2 × 10-4 M
Solution:
a) [OH–] = 0.05 M
pOH = – log (0.05)
= – log 5 × 10-2
= – log 5 + 2 log 10
= 2 – log 5
= 1.3010
pH = 14 – pOH
pH = 14 – 1.3010
= 12.699
b) [OH–] = 2 × 10-4 M
pOH = – log 2 × 10-4
= – log 2 + log 10
= 4 – log 2
= 4 – 0.3010
= 3.699
pH = 14 – 3.699 = 10.301
Question 31.
2g of NaOH is dissolved in water to give 1 litre solution. What is the pH of the solution ?
Solution:
N = \(\frac{w t}{G \in w} \times \frac{1}{1}\)
= \(\frac{2}{40}\) = \(\frac{1}{20}\) = 0.05 N = [OH–]
∴ pOH = – log 0.05
= – log 5 × 10-2
= 2 – log 5
= 1.3010
pH = 14 – pOH
= 13 – 1.3010
= 12.699
![]()
Question 32.
Calculate the pH of the following solutions.
a. 0.37 g of Ca(OH)2 dissolved in water to give 500 ml solution
b. 0.3 g of NaOH dissolved in water to give 200 ml solution
c. 0.1825% HCl aqueous solution
d. 1ml of 13.6 M HCl is diluted with water to give 1 litre solution.
Solution:
a) 0.37 gms of Ca(OH)2 in 500 ml
N = \(\frac{w t}{G \times w} \times \frac{1}{1}\)
N = \(\frac{0.37}{37} \times \frac{1000}{500}\)
= 0.01 × 2
= 0.02 = pOH
pOH = – log 0.02
= 1.699
pH = 14 – pOH = 12.301
b) 0.3 gms of NaOH in 200 mZ solution
N = \(\frac{0.3}{40} \times \frac{1000}{200}\)
= \(\frac{0.3 \times 5}{40}=\frac{1.5}{40}\)
= 0.375 = [OH–]
pOH = – log [OH–]
= – log 0.375
= 1.426
pH = 14 – pOH
= 14 – 1.426
= 12.574
c) 0.1825% HCl solution means 100 ml
solution contain 0.1825 g. of HCl
Normality (N) = \(\frac{W}{E W} \times \frac{1000}{V}\)
= \(\frac{0.1825}{36.5} \times \frac{1000}{100}\) = 0.05 N
∴ [H+] = 0.05 N
∴ pH = – log[H+]
= – log [0.051
= – log [5 × 10-2]
= 2 – log 5
= 2 – 0.692
∴ pH = 1.308
d) ∴ [H+] = 13.6
Diluted with water to 1 litre solution
∴ [H+] = \(\frac{13.6}{1000}\) = 0.016
pH = – log [H+]
= – log 0.0136 = 1.87
Question 33.
How many grams of NaOH are present in 100 ml solution if pH of the solution is 10?
Solution:
Given
pH = 10
pOH = 14 – 10 = 4
∴ Normality = 10-4 N
N = \(\frac{w t}{G M w} \times \frac{1000}{V(m l)}\)
10-4 = \(\frac{w t}{40} \times \frac{1000}{100}\)
∴ wt = 4 × 10-4 gms
Question 34.
The value of Kw is 9.55 × 10-14 at certain temperature. Calculate the pH of water at this temperature.
Solution:
Since Kw = [H+] [OH–]
Kw = 9.55 × 10-14 mol2/lit2
[H+] [OH–] = 9.55 × 10-14 mol2/lit2
∴ [H+] = \(\sqrt{9.55 \times 10^{-14}}\)
= 3.09 × 10-7 mol/lit
pH = – log[H+]
= – log [3.09 × 10-7]
= – [log 3.09 + log 10-7]
= – [0.49 – 7]
pH = 7 – 0.49 = 6.51
![]()
Question 35.
Calculate the pH of 10-8 M NaOH.
Solution:
The given box solution is very dilute. Hence OH– obtained from the box and water must be taken into consideration.
∴ [OH–] = 10-8 + 10-7 = 1.1 × 10-7
pOH = -log 1.1 × 10-7
pOH = 6.995
∴ pOH = 14 – 6.995 = 7.005
Question 36.
150 ml of 0.5 M HCl and 100 ml of 0.2 M HCl are mixed. Find the pH of the resulting solution.
Solution:
N = \(\frac{N_1 V_1+N_2 V_2}{V_1+V_2}\)
= \(\frac{150 \times 0.5+100 \times 0.2}{250}\)
= \(\frac{75+20}{250}=\frac{95}{250}\) = 0.38
pH = – log [H+] = – log 1 (0.38) = 0.42
Question 37.
Calculate the pH of solution obtained by mixing 10ml of 0.1 M HCl and 40ml of 0.2M H2SO4.
Solution:
M = \(\frac{10 \times 0.1+40 \times 0.4}{50}\)
= \(\frac{1+16}{50}=\frac{17}{50}\) = 0.34
pH = – log [H+]
= – log (0.34) = 0.4685
Question 38.
100 ml of pH = 4 solution is mixed with 100 ml of pH = 6 solution. What is the pH of resulting solution.
Solution:

Question 39.
Equal volumes of 0.5 M NaOH and 0.3 M KOH are mixed in an experiment. Find the pOH and pH of the resulting solution.
Solution:
N = \(\frac{N_1 V_1+N_2 V_2}{V_1+V_2}\)
N = \(\frac{x(0.5)+x(0.3)}{x+x}\) Given value equal
= \(\frac{0.8}{2}\) = 0.4 = [OH–]
pOH = – log [OH–]
= – log (0.4)
= 0.3979
pH = 14 – 0.3979
= 13.6021
![]()
Question 40.
60 m2 of 1 M HCl is mixed with 40 ml of 1 M NaOH. What is the pH of resulutant solution ?
Solution:
VANA > VBNB ⇒ N = \(\frac{V_A N_A-V_B N_B}{V_A+V_B}\)
∴ N = \(\frac{60-40}{60+40}\)
= \(\frac{20}{100}\) = \(\frac{1}{5}\) = 0.2
pH = – log [H+] = – log 0.2
= 0.699
Question 41.
Calculate the pH of a solution which contains 100 m2 of 0.1 M HCl and 9.9 m2 of 1.0M NaOH.
Solution:
Here VANA > VBNB
N = \(\frac{V_A N_A-V_B N_B}{V_A+V_B}\)
= \(\frac{10-9.9}{109.9}\)
= \(\frac{0.1}{109.9}\)
= 0.000909.
pH = – log [H+]
= – log (0.000909)
= 3.0416
Question 42.
What will be the resultant pH when 200 ml of an aqueons solution of HCl having pH = 2 is mixed with 300 m2 of an aqueous of NaOH having pH = 12?
Solution:
VA = 200 ml
NA = 10-2
[∵ pH = 2]
VB = 300 ml
NB = 10-2
[∵ pOH = 2]
∴ VBNB > VANA
∴ N = \(\frac{300 \times 10^{-2}-200 \times 10^{-2}}{300+200}\)
= \(\frac{1}{500}\) = 0.002 = [OH–]
pOH = – log [OH–]
= – log [0.002]
= -log 2 × 10-3
= – log 2 + 3 log 10
= 3 – log 2
= 2.699
∴ pH = 14 – pOH
= 14 – 2.699
= 11.3010
Question 43.
50 ml of 0.2 M HCl is added to 30 ml of 0.1 M KOH solution. Find pH of the solution.
Solution:
VA = 50 ml ; VB = 30 ml
NA = 0.2 N; NB = 0.1 ml
VANA > VBNB
∴ N = \(\frac{V_A N_A-V_B N_B}{V_A+V_B}\)
= \(\frac{50 \times 0.2-30 \times 0.1}{50+30}\)
= \(\frac{1-0.3}{80}=\frac{0.7}{80}\)
= 0.00875
∴ pH = – log [H+]
= – log (0.00875)
= 1.058.
![]()
Question 44.
40 ml of 0.2 M HNO3 when reacted with 60 ml of 0.3 M NaOH, gave a mixed solution. What is the pH ofo the resulting solution.
Solution:
VBNB > VANA
Question 45.
50 ml of 0.1 M H2SO4 were added to 100 ml of 0.2 M HNO3. Then the solution is diluted to 300 ml. What is the pH of the solution.
Solution:
V1 = 50 ml ; V2 = 100 ml
N1 = 0.1 × 2 = 0.2N ; N2 = 02N

Question 46.
What is the Kw value in an aqueons solution of pKw = 13.725
Solution:
Given pKw = 13.725
pKw = – log Kw
Kw = antilog of 13.725
= 1.884 × 10-14
Question 47.
The ionic product of water at 80°C is 2.44 × 10-13. What are the concentrations of hydroniumion and the hydroxide in pure water at 80°C?
Solution:
Kw = [H+] [OH–]
Kw = 2.44 × 10-13
For pure water [H+] = [OH–]
∴ [H+] = Kw
[H+] = \(\sqrt{2.44 \times 10^{-13}}\)
= 4.94 × 10-7 moles / lit
∴ [OH–] = 4.94 × 10-7 mole/lit
![]()
Question 48.
The ionization constant for water is 2.9 × 10-14 at 40°C. Calculate [H3O+], [OH]. pH and pOH for pure water at 40C.
Solution:
Kw = [H-1] [OH–]
2.9 × 10-14 = [H+] [OH–]
For pure water [H+] = [OH–]
∴ [H+]2 = 2.9 × 10-14
[H+] = 1.7 × 10-7 = [H3O+]
∴ [OH–] = 1.7 × 10-7
pH = – log [H+]
= -log [1.7 × 10-7]
= 7 – log 1.7 = 6.7689
pOH = – log [OH–]
= – log [1.7 × 10-7]
= 7 – log 1.7 = 6.7689
Question 49.
Calculate the pH of
a. 0.002 M acetic acid having 2.3% dissociation.
b. 0.002 M NH4OH having 2.3% dissociation.
Solution:
a) [H+] = Cα
= 0.002 × 2.3 = 0.0046
pH = – log [H+]
= – log 0.0046
= 4.3372
b) [OH–] = Cα
= 0.002 × 2.3
= 0.0046
pOH = – log [OH–]
= – log 0.0046
= 4.3372
pH = 14 – pOH
= 14 – 4.3372
= 9.6628
Question 50.
Calculate Ka of acetic acid from equilibrium concentration given below
[H3O+] = [CH3COO–] = 1.34 × 10-3M, [CH3COOH] = 9.866 × 10-2 M
Solution:
Given
[H3O+] = [CH3COO–] = = 1.34 × 10-3 M
[CH3COOH] = 9.866 × 10-2 M
Ka = \(\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}\right]}\)
= \(\frac{1.34 \times 10^{-3} \times 1.34 \times 10^{-3}}{9.866 \times 10^{-2}}\)
= 1.819 × 10-5
![]()
Question 51.
Calculate pH of 0.1 M acetic acid having Ka =1.8 × 10-5.
Solution:

Question 52.
The pH of 0.1 M solution of weak mono protic acid is 4.0 calculate its [H+] and Ka.
Solution:
Given pH = 4.0
∴ [H+] = ?
pH = – log[H+]
[H+] = 10-pH
= 10-4
∴ [H+] = C × α
α = \(\frac{10^{-4}}{0.1}\)
= 10-3
Ka = C × α2
= 0.1 × (10-3)2
= 0.1 × 10-6
= 10-7.
Question 53.
Ka of 0.02 M CH3 COOH is 1.8 × 10-5. Calculate
a. [H3O+]
b. % ionization
c. pH
Solution:
(a), (b)
d2 = \(\frac{K_a}{C}\)
= \(\frac{1.8 \times 10^{-5}}{0.02}\)
α2 = 9 × 10-4
α = 3 × 10-2
% of ionisation
[H3O+] = C × α
= 0.02 × 3 × 10-2 = 6 × 10-4
c) pH = -log[H3O+]
= -log(6 × 10-4) = 3.24.
![]()
Question 54.
Calculate the pH of 0.01 M solution of CH3 COOH. Ka for CHa OOH at 298K is 1.8 × 10-5.
Solution:
α2 = \(\frac{K_a}{C}\)
= \(\frac{1.8 \times 10^{-5}}{0.01}\)
= 180 × 10-5
= 18 × 10-4
α = 4.1 × 10-2
∴ [H3O+] = 0.01 × 4.1 × 10-2
= 4.1 × 10-4
pH = – log [H3O+]
= -log (4.1 × 10-4) = 3.38.
Question 55.
The pH of 0.1 M solution of an organic acid is 4.0 calculate the dissociation constant of the acid.
Solution:
Given pH = 4.0
∴ [H+] = ?
pH = – log[H+]
∴ [H+] = 10-pH = 10-4
∴ [H+] = C × α
α = \(\frac{10^{-4}}{0.1}\) = 10-3
Ka = C × α2
= 0.1 × (10-3)2 = 0.1 × 10-6 = 10-7
Question 56.
Three ionization constants for HF, HCOOH and HCN at 298 K are 6.8 × 10-4, 1.8 × 10-4 and 4.8 × 10-9 respectively. Calculate the ionization constants of the corresponding conjugate base.
Solution:
i) Consider the case of HF
Ka = 6.8 × 10-4
Kb = \(\frac{\mathrm{K}_{\mathrm{W}}}{\mathrm{K}_{\mathrm{a}}}=\frac{1 \times 10^{-14}}{6.8 \times 10^{-4}}\) = 0.147 × 10-10
ii) Consider the case of HCOOH
Ka = 1.8 × 10-4
Kb = \(\frac{K_w}{K_a}=\frac{1 \times 10^{-14}}{1.8 \times 10^{-4}}\) = 0.56 × 10-10
iii) Consider the case of HCN
Ka = 4.8 × 10-9
Kb = \(\frac{\mathrm{K}_{\mathrm{w}}}{\mathrm{K}_{\mathrm{a}}}=\frac{1 \times 10^{-14}}{4.8 \times 10^{-9}}\) = 0.208 × 10-5
Question 57.
Find the concentration of hydroxide ion in a 0.25 M solution of trimethylamine, a weak base.
(CH3)3N + H2O ⇌ (CH3)3N+H+OH–; Kb = 7.4 × 10-5.
Solution:
σα = \(\sqrt{\frac{K_b}{c}}=\sqrt{\frac{7.4 \times 10^{-5}}{0.25}}\)
= 1.74 × 10-3
[OH–] = c × α
= 0.25 × 1.74 × 10-3
= 4.32 × 10-3 M
![]()
Question 58.
The 0.005 M monobasic acid has a pH of 5. What is the extent of ionization ?
Solution:
pH = 5
∴ [H+] = 10-5
Concentration (C) = 0.005 M = 5 × 10-3 M
[H+] = Cα
α = degree of dissociation per mole = ?
∴ α = \(\frac{\left[\mathrm{H}^{+}\right]}{\mathrm{C}}=\frac{\left[\mathrm{H}^{+}\right]}{5 \times 10^{-3}}=\frac{10^{-5}}{5 \times 10^{-3}}\)
= \(\frac{1}{5}\) × 10-2 = 0.2 × 10-2
Percentage of degree of dissociates
= 0.02 × 10-2 × 100 = 0.2 %
Question 59.
50 ml of 0.1 M NH4OH, 25m1 of 2 M NH4Cl were used to make a buffer. What is the pH if PKa is 4.8.
Solution:
The given buffer is a base buffer.
For a base buffer pOH = pKb + log \(\frac{[\text { Salt }]}{[\text { Base }]}\)
∴ pOH = 4.8 + \(\log \left\{\frac{\frac{(25 \times 2)}{75}}{\frac{(50 \times 0.1)}{75}}\right\}\)
= 4.8 + log(10) = 4.8 + 1 = 5.8
∴ pH = (14.0 – pOH) = (14.0 – 5.8) = 8.2
∵ pH + pOH = 14.0 at room temperature.
Question 60.
The pH of a buffer prepared by mixing 50 ml of 0.2 M CH3 COOH and 25 ml of CH3 COONa is 4.8. If the PKa is 4.8. What is the strength of CH3 COONa.
Solution:
The given solution is an acid buffer.
∴ The pHof the buffer is given by,
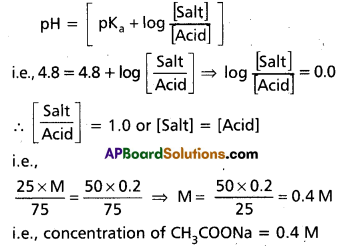
Question 61.
50 ml of 0.1 M sodium acetate, 25ml of 0.2 M acetic acid were added together to form the buffer solution. PKa of CH3 COOH is 4.8 Find the pH of the solution.
Solution:
The buffer solution is an acid buffer.
Hendersen’s equation for an acid buffer is
pH = pKa + log
\(\frac{[\text { Salt }]}{[\text { Base }]}=4.8+\left\{\log \frac{\frac{(0.1 \times 50)}{75}}{\frac{(0.2 \times 25)}{75}}\right\}\)
= 4.8 + log (1)
∴ pH = 4.8.
![]()
Question 62.
When 20 ml of 0.1 M NH4OH are added to 20ml of 1M NH4Cl solution, the pH of the buffer formed is 8.2. What is the pKa of NH4OH?
Solution:
For base buffer, pH is given by
pH = 14.0 – pOH and pOH
= pKb + \(\log \frac{[\text { Salt }]}{[\text { Base }]}\)
The pH of the buffer = 8.2;
∴ pOH =(14 – pH) = 5.8 then
5.8 = pKb + \(\log \frac{[\text { Salt }]}{[\text { Base }]}\)
= pKb + \(\log \left[\frac{\frac{20 \times 1}{40}}{\frac{20 \times 0.1}{40}}\right]\)
= pKb + log (10) = (pKb + 1.0)
∴ pKb = (5.8 – 1) = 4.8
Question 63.
One litre of buffer solution contains 0.1 mole of aceticacid add 1 mole of sodium acetate. Find its pH if PKa of CH3COOH is 4.8.
Solution:
For an acid buffer pH = PKa + \(\log \frac{[\text { Salt }]}{[\text { Base }]}\)
pH = 4.8 + log \(\frac{1}{0.1}\) = 4.8 + log 10
pH = 4.8 + 1 ⇒ pH = 5.8
Question 64.
50 ml of 1 M CH3 COOH solution, when added to 50 ml of 0.5 M NaOH gives a solution with a pH ‘X’. Find the value of ‘X’. PKa of acetic acid is 4.8.
Solution:
Acetic acid reacts with sodium hydroxide to form sodium acetate.
CH3COOH + NaOH → CH3COONa + H2O
No.of millimoles of CH3COOH = 50 × 1 = 50
No.of millimoles of NaOH = 50 × 0.5 = 25
No.of millimoles of CH3. COOH remained unreacted = 50 – 25 = 25
Total Vol. of solution = 50 + 50 = 100 ml
No. of millimoles of CH3COONa formed = 25
∴ Molarity of CH3COONa = \(\frac{25}{100}\) = .25 M
Molarity of CH3COOH = \(\frac{25}{100}\) = .25 M
pH = pKa + \(\log \frac{[\text { Salt }]}{[\text { Base }]}\)
pH = 4.8 + log \(\frac{1}{0.1}\) = 4.8 + log 10
= 4.8 + log \(\frac{.25}{.24}\) = 4.8 + log(1)
∴ pH of the solution = 4.8 + 0 = 4.8
Question 65.
The solubility product of AgCl is 1.6 × 10-10 mol2/L2. What is solubility?
Solution:
KSP = S2
1.6 × 10-10 = S2
∴ S = \(\sqrt{10^{-10} \times 1.6}\) = 1.3 × 10-5 moles /litre.
![]()
Question 66.
The solutbility product of Zr (OH)2 is 4.5 × 10-17 mol3L-3 what is solubility?
Solution:
Zn(OH)2 ⇌ Zn++ + 2OH–
∴ KSP = S × 4S2 = 4S3
∴ 4S3 = 4.5 × 10-17
S3 = 4.5 × 10-18/4 = 11.7 × 10-18
S = \(\sqrt[3]{11.7} \times \sqrt[3]{10^{-18}}\)
S = 2.6 × 10-6
Question 67.
The solubility of Ag2 CrO4 is 1.3 × 10-4 mol L-1. What is the solubility product ?
Solution:
![]()
KSP = 4S2 × S = 4S3
∴ KSP = 4 × S3
= 4 × (1.3 × 10-4)3
KSP = 9 × 10-12
Question 68.
The solubility of A2B = 2 × 10-3 mol L-1. What is solubility product?
Solution:
KSP = [2s]2[S]
S = 3\(\sqrt{\frac{K_{S P}}{4}}\)
= 3\(\sqrt{\frac{2 \times 10^{-3}}{4}}\) = 3.2 × 10-10
Question 69.
The sotubility product of a salt AB = 10-10 mol2 L-2. What is solubility?
Solution:
KSP = s2
S = \(\sqrt{K_{s p}}=\sqrt{10^{-10}}\) = 10-5 moles/lit
Question 70.
PQ and RS2 are two sparingly soluble salts. Their solubility products are equal and each equal to 4.0 × 10-18. Which salt is more soluble ?
Solution:
Given KSP of PQ and RS2 salts = 4 × 10-18
S = \(\sqrt{\frac{K_{\mathrm{SP}}}{4}}\) for RS2
S = \(\sqrt{K_{s p}}\) for PQ
∴ Solubility of RS2 is more.
![]()
Question 71.
In a 0.1 M solution, acetic acid is 1.34% ionized. Calculate [H+], [CH3COO–] and [CH3COOH] in the solution and Calculate Ka of acetic acid.
Solution:
Given 1.34 % ionised
[H+] = C × α
= 0.1 × 1.34 × 10-2 = 1.34 × 10-3 M
∴ [CH3COOH] =1.34 × 10-3 M
[H+] = Cα = 1.34 × 10-3]
α = \(\frac{1.34 \times 10^{-3}}{0.1}\) = 1.34 × 10-2]
[CH3COO–] (1 – α) = 0.1 (1 – 0.0134)
= 0.09866 M
Ka = α2 × C
= (1.34 × 10-2) × 0.1 = 1.79 × 10-5
Solved Problems
Question 1.
The following concentrations were obtained for the formation of NH3 from N2 and H2 at equilibrium at 500 K. [N2] = 1.5 × 10-2 M. [H2] = 3.0 × 10-2 M and [NH3] = 1.2 × 10-2 M. Calculate equilibrium constant.
Solution:
The equilibrium constant for the reaction. N2(g) + 3 H2 (g) ⇌ NH3(g) can be written as,

Question 2.
At equilibrium, the concentrations of N2 = 3.0 × 10-3 M, O2 = 4.2 × 10-3 M and NO = 2.8 × 10-3 M in sealed vessel at 800K. What will be Kc for the reaction
N2(g) + O2 (g) ⇌ 2 NO(g)
Solution:
For the reaction equilibrium constant, KC can be written as,
KC = \(\frac{[\mathrm{NO}]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{O}_2\right]}\)
= \(\frac{\left(2.8 \times 10^{-3} \mathrm{M}\right)^2}{\left(3.0 \times 10^{-3} \mathrm{M}\right)\left(4.2 \times 10^{-3} \mathrm{M}\right)}\)
= 0.622
Question 3.
PCl5, PCl3 and Care at equilibrium at 500 K and having concentration 1.59 M PCl3, 159M Cl2 and 1.41 M PCl5, Calculate K for the reaction
PCl5 ⇌ PCl3 + Cl2
Solution:
The equilibrium constant K. for the above reaction can be written as,
KC = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}=\frac{(1.59)^2}{(1.41)}\) = 1.79
![]()
Question 4.
The value of KC = 4.24 of 800 K for the reaction
CO (g) + H2O (g) ⇌ CO2 (g) + H2 (g)
Calculate equilibrium concentrations of CO2, H2, CO and H2O at 800 K, if only CO and H2O are present initially at concentrations of 0.10 M each.
Solution:
For the reaction,

where x is the amount of CO2 and H2 at equilibrium.
Hence, equilibrium constant can be written as,
KC = x2/(0.1 – x)2 = 4.24
x2 = 4.24(0.01 + x2 – 0.2 x)
x2 = 0.0424 + 4.24 x2 – 0.848 x
3.24 x2 – 0.848 x + 0.0424 = 0
a = 3.24, b = – 0.848, c = 0.0424
(for quadratic equation ax2 + bx + c = 0
x = \(\frac{\left(-b \pm \sqrt{b^2-4 a c}\right)}{2 a}\)
x = 0.848 ± \(\sqrt{(0.848)^2}\) – 4(3.24) (0.04224) / (3.24 × 2)
x = (0.848 ± 0.4118)/6.48
x1 = (0.848 – 0.4118)] 6.48 = 0.067
x2 = (0.848 + 0.4118)/6.48 = 0.194
the value 0.194 should be neglected because it will give concentration of the reactant which is more than initial concentration. Hence the equilibrium concentrations are,
[CO2] [H2] = x = 0.067 M
[CO] = [H2O] = 0.1 – 0.067 = 0.033 M
Question 5.
For the equilibrium, 3 NOCl (g) ⇌ 2 NO(g) + C2 (g) the value of the equilibrium constant, KC is 3.75 × 10-6 at 1069 K. Calculate the Kp for the reaction at this temperature ?
Solution:
We know that,
KP = KC(RT)∆n
For the above reaction,
∆n = (2 + 1) – 2 = 1
KP = 3.75 × 10-6 (0.0831 × 1069)
KP = 0.033
Question 6.
The value of KP for the reaction.
CO2 (g) + C(s) ⇌ 2CO (g) is 3.0 at 1000 K. If initially PCO2 = 0.48 bar and PCO = 0 bar and pure graphite is present, calculate the equilibrium partial pressures of CO and CO2.
Solution:
For the reaction,
let ‘x’ be the decrease in pressure of CO2, then

= (-3 ± 5.66)/8
= (-3 + 5.66)/8 (as value of x cannot be negative hence we neglect that value)
x = 2.66/8 = 0.33
The equilibrium partial pressures are,
PCO = 2x = 2 × 0.33 = 0.66 bar
PCO2 = 0.48 – x = 0.48 – 0.33 = 0.15 bar
![]()
Question 7.
The value of Kc for the reaction
2A ⇌ B + C is 2 × 10-3. At a given time, the composition of reaction mixture is [A] = [B] = [C] = 3 × 10-4 M. In which direction the reaction will proceed ?
Solution:
For the reaction the reaction quotient QC is given by.
QC = [B] [C] / [A]2
as [A] = [B] = [C] = 3 × 10-4 M
QC = (3 × 10-4) (3 × 10-4)/ (3 × 10-4)2 = 1
as QC > KC so the reaction will proceed in the reverse direction.
Question 8.
13.8 g of N2O4 was placed in a 1L reaction vessel at 400 K and allowed to attain equilibrium
N2O4(g) ⇌ 2 NO2(g)
The total pressure at equilbrium was found to be 9.15 bar. Calculate KC, KP and partial pressure at equilibrium.
Solution:
We know pV = nRT
Total volume (V) = 1 L
Molecular mass of N2O4 = 92 g
Number of moles = 13.8 g / 92 g = 0.15 of the gas (n)
Gas constant (R) = 0.083 bar L mol-1K-1
Temperature (T) = 400 K
pV = nRT
p × 1L = 0.15 mol × 0.083 bar L mol-1K-1 × 400 K
p = 4.98 bar
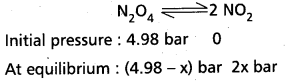
Hence,
ptotal at equilibrium = pN2O4 + pNO2
9.15 = (4.98 – x) + 2x
9.15 = 4.98+ x
x = 9.15 – 4.98 = 4.17 bar
Partial pressures at equilibrium are,
pN2O4 = 4.98 – 4.17 = 0.81 bar
pNO2 = 2x = 2 × 4.17 = 8.34 bar
Kp = (pNO2)2 / pN2O4
= (8.34)2 / 0.81 = 85.87
Kp = KC (RT)∆n
85.87 = KC(0.083 × 400)1
KC = 2.586 = 2.6
![]()
Question 9.
300 mol of PCl5 kept in 1L closed reaction vessel was allowed to attain, equilibrium at 380K. Calculate composition of the mixture at equilibrium. Kc = 1.80
Solution:

Question 10.
The value of ∆G° for the phosphorylation of glucose in glycolysis is 13.8 kJ/mol. Find the value of Kc at 298 K.
Solution:
∆G° = 13.8 ki/ mol = 13.8 × 103J/mol
Also, ∆G° = – RT Inkc
Hence, In Kc = – 13.8 × 103 J/mol
(8.314 Jmol-1K-1 × 298 K)
In Kc = 5.569
Kc = e-5 569
Kc = 3.81 × 10-3
Question 11.
Hydrolysis of sucrose gives.
Sucrose + H2O ⇌ Glucose + Fructose Equilibrium constatnt Kc for the reaction is 2 × 1013 at 300K. Calculate ∆GΘ at 300K.
Solution:
∆G° = -RT InKc
∆G° = -8.314J mol-1K-1 × 300K × In (2 × 1013)
∆G° = – 7.64 × 104J mo-1
Question 12.
What will be the conjugate bases for the following Bronsted acides: HF, H2SO4 and \(\mathrm{HCO}_3^{-}\) ?
Solution:
The conjugate bases should have one proton less in each case and therefore the corresponding conjugate bases are: F–, \(\mathrm{HSO}_3^{-}\) and CO2-3 respectively.
![]()
Question 13.
Write the conjugate acids for the following Bronsted bases: NH–2, NH3 and HCOO–.
Solution:
The conjugate acid should have one extra proton in each case and therefore the corresponding conjugate acids are : NH3, NHO+4 and HCOOH respectively.
Question 14.
The species; H2O, \(\mathrm{HCO}_{3^{\prime}}^{-}\), \(\mathrm{HCO}_{4^{\prime}}^{-}\) and NH3 can act both as Bronsted acids andbases. For each case give the corresponding conjugate acid and conjugate base.
Solution:
The answer is given in the following Table:
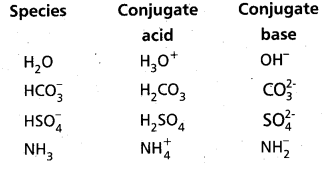
Question 15.
Classify the following species into Lewis acids and Lewis bases and show how these act as such :
(a) HO–
(b) F–
(c) H+
(d) BCl3
Solution:
(a) Hydroxyl ion is a Lewis base as it can donate an electron lone pair (: OH–).
(b) Flouride ion acts as a Lewis base as it can donate any one of its four electron lone pairs.
(c) A proton is a Lewis acid as it can accept a lone pair of electrons from bases like hydroxyl ion and fluoride ion.
(d) BCl2 acts a Lewis acid as it can accept a lone pair of electrons from species like ammonia or amine molecules.
Question 16.
The concentration of hydrogen ion in a sample of soft drink is 3.8 × 10-3M. What is its pH ?
Solution:
pH = – Log[3.8 × 10-3]
= -{log[3.8] + log[10-3}]
= – {(0.58) + (-3.0)} = -2.42} = 2.42
Therefore, the pH of the soft drink is 2.42 and it can be inferred that it is acidic.
![]()
Question 17.
Calculate pH of a 1.0 -8 M solution of HCl.
Solution:
2H2O(1) H3O+ (aq) + OH–(aq)
Kw = [OH–][H3O+]
= 10-14
Let, x = [OH–] = [H3O+] from H2O. The H3O+ concentration is generated (i) from the ionization of HCl dissolved i.e., HCl (aq) + H2O (1) ⇌ H3O+ (aq) + Cl–(aq), and (ii) from ionization of H2O. Inthese very dilute solutions. both sources of H3O+ must be considered:
[H3O+] = 10-8 + X
Kw = (10-8 + x)(x) = 10-14
or x2 + 10-8 x – 10-14 = 0
[OH–] = x = 9.5 × 10-8
So, pOH = 7.02 and pH = 6.98
Question 18.
The ionization costant of HF is 3.2 × 10-4. Calculate the degree of dissociation of HF in its 0.02 M solution. Calculate the concentration of all species present (H3O+.F– and HF) in the solution and its pH.
Solution:
The following proton transfer reactions are possible :
1) HF + H2O ⇌ H3O+F–Ka = 3.2 × 10-4
2) H2O + H2O H3O+ + OH– Kw = 1.0 × 10-14
As ka >> Kw, [1] is the principle reaction.
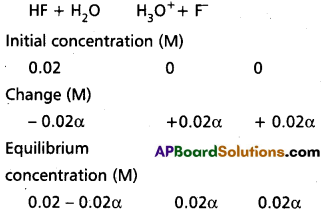
Substituting equilibrium concentrations in the equailibrium reaction for principal reaction gives.
Ka (0.02α)2/ (0.02 – 0.02α)
= 0.02α2/(1 – α) = 3.2 × 10-4
We obtain the following quadratic equation:
α2 + 1.6 × 10-2α – 1.6 × 10-2 = 0
The quadratic equation in α can be solved and the two values of the roots are :
α = + 0.12 and – 0.12
The negative root is not acceptable and hence.
a = 0.12
This means that the degree of ionization α = 0.12, then equilibrium concentrations of other species viz., HF, F– and H3O+ are given by:
[H3O+] = [F] = cα = 0.02 × 0.12
= 2.4 × 10-3M
[HF] = c(1 – α) = 0.02(1 – 0.12)
= 17.6 × 10-3M
pH = -log[H+] = -log (2.4 × 10-3) = 2.62
![]()
Question 19.
The pH of 0.1 M monobasic acid is 4.50. Calculate the concentration of species H+, A– and HA at equilibrium. Also, determine the value of Ka and pKa of the monobasic acid.
Solution:
pH = – log [H+]
Therefore [H+] = 10-pH = 10-4.50
= 3.16 × 10-5
[H+] = [A–] = 3.16 × 10-5
Thus, Ka = [H+] [A–] / [HA]
[HA]eqlbm = 0.1 – (3.16 × 10-5) ≅ 0.1
Ka = (3.16 × 10-5)2/0.1 = 1.0 × 10-8
pKa = – log (10-8) = 8
Alternatively, “Percent dissociation” is another useful method for measure of strength of a weak acid and is given as : Percent dissociation
= [HA]dissociated × 100/[HA]initial (7.32)
Question 20.
Calculate the pH of 0.08M solution of hypochlorous acid. HOCI. The ionization Constant of the acid is 2.5 × 10-5, Determine the percent dissociation of HOCl
Solution:

[H+] = 1.41 × 10-3 M Therefore,
Percent dissociation
= {[HOCI]dissociated × 100/[HOCI]initial}
= 1.41 × 10-3 /0.08 = 1.76%,
pH = -log (1.41 × 10-3) = 2.85
Question 21.
The pH of 0.004 M hydrazine solution is 9.7. Calculate is ionization constant Kb and pKb.
Solution:
NH2NH2 + H2O ⇌ \(\mathrm{NH}_2 \mathrm{NH}_3^{+}\) +OH–
From the pH we can calculate the hydrogen ion concentration. Knowing hydrogen ion concentration and the ionic product of water we can calculate the concentration of hydroxyl ions. Thus we have :
[H+] = antilog (-pH)
= antilog (-9.7) = 1.67 × 10-10
[OH–] = Kw/[H+] = 1 × 10-14/ 1.67 × 10-10
= 5.98 × 10-5
The concentration fo the corresponding hydrazinium ion is also the same as that of hydroxyl ion. The concentrations of both these ions are very small so the concentration of the undissociated base can be taken equal to 0.004 M.
Thus,
Kb = [NH2NH3+] [OH–] / [NH2NH2]
= (5.98 × 10-5)2/0.004 = 8.96 × 10-7
pKb = -logKb = -log(8.96 × 10-7 ) = 6.04
![]()
Question 22.
Calculate the pH of the solution in which 0.2M NH4Cl and 0.1 M NH3 are present. The pKb of ammonia solution is 4.75.
Solution:
NH3 + H2O ⇌ \(\mathrm{NH}_4^{+}\) + OH–
The ionization constant of NH3,
Kb= antilog (-pKb) i.e.
Kb = 10-4.75 = 1.77 × 10-5 M
3 + H2O ⇌ \(\mathrm{NH}_4^{+}\) + OH– Initial concentration (M)

Change in concentration to reach equilibrium (M)

Kb = [latex]\mathrm{NH}_4^{+}[/latex][OH-1] / [NH3]
= (0.20 × x) (x) / (0.1 – x) = 1.77 × 10-5
As Kb is small, we can neglect x in comparison to 0.1 M and 0.2 M. Thus
[OH–] = x = 0.88 × 10-5
Therefore, [H+] = 1.12 × 10-9
pH = -log [H+] = 8.95 .
Question 23.
Determine the degree of ionization and pH of a 0.05M of ammonia solution. The ionization constant of ammonia can be taken from Table 7.7. Also, calculate the ionization constant of the conjugate acid of ammonia.
Solution:
The ionization of NH3 in water is represented by equation :
NH3 + H2O ⇌ \(\mathrm{NH}_4^{+}\) + OH–
We use equation (7.33) to calculate hydroxyl ion concentration,
[OH–] c α = 0.05 α
Kb = 0.05 α2/(1 – α)
The value of α is small, therefore the quadratic equation can be simplified by neglecting a in comparison to 1 in the denominator on right hand side of the equation,
Thus,
Kb = C α2 or α = \(\sqrt{\left(1.77 \times 10^{-5} / 0.05\right)}\)
= 0.018.
[OH–] = C α = 0.05 × 0.018 = 9.4 × 10-4 M.
[H+] = Kw/[OH–] = 10-14 / (9.4 × 10-4)
= 1.06 × 10-11
pH = -log (1.06 × 10-11) = 10.97
Now, using the relation for conjugate acid-base pair,
Ka × Kb = Kw
using the value of Kb of NH3 from Tabel 7.7.
We can determine the concentration of con-jugate acid \(\mathrm{NH}_4^{+}\)
Ka × Kw/ Kb = 10-14/ 1.77 × 10-5
= 5.64 × 10-10.
![]()
Question 24.
Calculate the pH of a 0.10M ammonia solution. Calculate the pH after 50.0 mL of this solution is treated with 25.0 mL of 0.10M HCl. The dissociation constant of ammonia, Kb = 1.77 × 10-5.
Solution:
NH3 + H2O ⇌ \(\mathrm{NH}_4^{+}\) + OH–
Kb = [latex]\mathrm{NH}_4^{+}[/latex] [OH–] / [NH3] = 1.77 × 10-5
Before neutralization,
[latex]\mathrm{NH}_4^{+}[/latex] [OH–] = x
[NH3] = 0.10 – x – 0.10, x2 / 0.10 = 1.77 × 10-5
Thus, x= 1.33 × 10-3 = [OH–]
Therefore, [H+] = Kw / [OH–] = 10-14 / (1.33 × 10-3)= 7.51 × 10-12
pH = -log (7.5 × 10-12 ) = 11.12
On addition of 25 mL of 0.1 M HCl solution (i.e., 2.5 mmol of HCl) to 50 mL of 0.1 M ammonia solution (i.e., 5 mmol of NH3), 2.5 mmol of ammonia molecules are neutralized. The resulting 75 mL solution contains the remaining unneutralized 2.5 mmol of NH3 molecules and 2.5 mmol of \(\mathrm{NH}_4^{+}\)

The resulting 75 mL of solution contains 2.5 mmol of \(\mathrm{NH}_4^{+}\) ions (i.e., 0.033M) and 2.5 mmol (i.e., 0.033M) of uneutralised NH3 molecules. This NH3 exists as NH4OH in the following equilibrium :
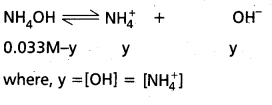
The final 75 mL solution after neutralisation already contains 2.5 m mol [latex]\mathrm{NH}_4^{+}[/latex] ions (i.e. 0.033M), thus total concentration of [latex]\mathrm{NH}_4^{+}[/latex] ions is given as : [NHJ] = 0.033 + y
As y is small, [NH4OH] ≃ 0.033 M and [latex]\mathrm{NH}_4^{+}[/latex] ≃ 0.033M.
We know,
Kb = [latex]\mathrm{NH}_4^{+}[/latex] [OH–] / [NH4OH]
= y(0.033)/(0.033) 1.77 × 10-5 M
Thus, y = 1.77 × 10-5 = [OH–]
[H+] = 10-14/ 1.77 × 10-5 = 0.56 × 10-9
Hence, pH = 9.24
Question 25.
The pKa of acetic acid and pKa of ammonium hydroxide are 4.76 and 4.75 respectively. Calculate the pH of am-monium acetate solution.
Solution:
pH = 7 + 1/2 [pKa – pKb]
= 7 + 1/2 [4.76 – 4.75]
= 7 + 1/2 [0.01] = 7 + 0.005 = 7.005
Question 26.
Calculate the solubility of A2X3 in pure water, assuming that neither kind of ion reacts with water. The solubility product of A2X3, Ksp = 1.1 × 10-23.
Solution:
A2X3 ⇌ 2A3+ + 3X2-
Ksp = [A3+]2 [X2-]3 = 1.1 × 10-23
If S = solubility of A2X3, then
[A3+] = 2S; [X2-] = 3S
therefore, Ksp = (2S)2 (3S)3 = 108S5
= 1.1 × 10-23
thus, S5 = 1 × 10-23
S = 1.0 × 10-5 mol/L.
![]()
Question 27.
The values of Ksp of two sparingly soluble salts Ni(OH)2 and AgCN are 2.0 × 10-15 and 6 × 10-17 respectively. Which salt is more soluble ? Explain.
Solution:
AgCN ⇌ Ag+ + CN–
Ksp = [Ag+] [CN–] = 6 × 10-17
Ni(OH)2 ⇌ Ni2 + 2OH–
Ksp = [Ni2+] [OH–]2 = 2 × 10-15
Let [Ag+] = S1 then [CN–] = S1
Let [Ni2+] = S2 then [OH–] = 2S2
S12 = 6 × 10-17 = S1 = 7.8 × 10-9
(S2) (2S2)2 = 2 × 10-15, S2 = 0.58 × 10-4
Ni(OH)2 is more soluble than AgCN.
Question 28.
Calculate the molar solubility of Ni(OH)2 in 0.10 M NaOH. The ionic product of Ni(OH)2 is 2.0 × 10-15.
Solution:
Let the solubility of Ni(OH)2 be equal to S. Dissolution of S mol/L of Ni(OH)2 provides S mol/L of Ni2+ and 2S mol/L of OH–, but the total concentration of OH– = (0.10 + 2S) mol/L because the solution already contains 0.10 mol/L of OH– from NaOH.
Ksp = 2.0 × 10-15 = [Ni2+] [OH–]2
(S) (0.10 + 2S)2 As Ksp is small, 2S < < 0.10,
thus, (0.10 + 2S) ≈ 0.10
Hence,
2.0 × 10-15 S(0.10)2
S = 2.0 × 10-13 M = [Ni2+]