Andhra Pradesh BIEAP AP Inter 1st Year Chemistry Study Material 6th Lesson Thermodynamics Textbook Questions and Answers.
AP Inter 1st Year Chemistry Study Material 6th Lesson Thermodynamics
Very Short Answer Questions
Question 1.
What is the information given by the term thermodynamics?
Answer:
- Thermodynamics gives information on energy changes involved in a chemical reaction (or) process.
- The laws of thermodynamics deal with energy changes in macroscopic systems involving a large no.of molecules.
Question 2.
What is the relationship between the laws of thermodynamics and the equilibrium state?
Answer:
- Laws of thermodynamics apply only when a system is in equilibrium (or) moves from one equilibrium state to another equilibrium state.
- Macroscopic properties like pressure and temperature do not change with time for a system in an equilibrium state.
![]()
Question 3.
Define a system. Give an example.
Answer:
System : A small part of the universe chosen for thermodynamic study is called system.
Question 4.
The wall is adiabatic and AU = Wad. What do you understand about the heat and work with respect to the system ?
Answer:
- In adiabatic process there is no transfer of heat between system and surroundings.
- Work done adiabatic process is the change in internal energy of the system.
Work done in adabatic process Wad = U2 – U1 = ∆U - Here work done on the system is positive and work done by the system is negative.
Question 5.
The system loses ‘q’ amount of heat though no work is done on the system. What type of wall does the system have ?
Answer:
- Here heat is transferred through a thermally conducting walls.
- In this case charge in internal energy ∆U = q can be measured interms of temperature difference.
q = TB – TA - Here no work is done at constant volume,
q = +ve → heat transferred from surrounding to system.
q = -ve → heat transferred from system to surrounding.
![]()
Question 6.
Work is done by the system and ‘q’ amount at heat is supplied to the system. What type of system would it be ?
OR
Work is done by the system and heat (q) is supplied to the system. What type of system would it be ?
Answer:
The system is closed system .
Mathematical form
∆U = q – W
∆U = Change in internal energy
q = heat supplied
W = Workdone by the system.
Question 7.
What is the workdone in the free expansion of an ideal gas in reversible and irreversible processes ?
Answer:
In case of free expansion of an ideal gas pressure becomes zero, (into vaccum) .
∴ No workdone during free expansion of an ideal gas in case to reversible as well as irreversible process.
Question 8.
From the equation ∆U = q-pex∆V, if the volume is constant what is the value of ∆U.
Answer:
Suppose volume is constant change in volume ∆V = 0
∆U = q = pex∆V
∆U = q – 0
∆U = q
∴ Internal energy change = heat supplied.
Question 9.
In isothermal free expansion of an ideal gas find the value of q and ∆U.
Answer:
∆U = q + W
In case of free expansion of a gas in isothermal process.
W = 0, q = 0, ∆U = 0
Work done W = 0 (∵ Pexp = 0)
∴ q = 0, U = 0
![]()
Question 10.
In isothermal irreversible change of ideal gas what is value of q ?
Answer:
In case of an isothermal irreversible change,
q = W = 0
q = -W
= pexp(Vf – Vi)
Question 11.
In isothermal reversible change of an ideal gas, what is the value of q ?
Answer:
In case of isothermal irreversible change
q = W
q = nRTln \(\frac{V_f}{V_i}\)
q = 2.303 nRT log \(\frac{V_f}{V_i}\)
Question 12.
For an adiabatic change is an ideal gas what is the relationship between its ∆U and W (adiabatic) ?
Answer:
For an adiabatic change q = 0
∆U = q + W
∆U = 0 + W
∆U = W
Change in internal energy = Work done in adiabatic process.
Question 13.
State the first law of the thermodynamics.
Answer:
First law of thermodynamics :
The law of conservation of energy is taken as the first law of thermodynamics.
Statements :
- “Energy can neither be created nor destoyed, although it can be transformed from one form to another”.
- “It is impossible to construct perpetual motion machine of first kind”.
- “The total energy of the system, and surroundings in constant”.
![]()
Question 14.
What are the sign conventions of the work done on the system and work done by the system ?
Answer:
- Work done on the system uses positive sign.
- Work done by the system uses negative sign.
Question 15.
Volume (V), pressure (P) and Temperature (T) are state functions. Is the statement true ?
Answer:
Volume (V), Pressure (P) and Temperature (T) are state functions. These do not depends upon path or reaction but only depends upon state of reaction.
Question 16.
What are the heat (q) sign conventions when heat is transferred from the surroundings to the system and that transferred from system to the surrounding ?
Answer:
q = positive → Heat transferred from surrounding to the system.
q = negative → Heat transferred from system to the surroundings.
Question 17.
No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have ?
Answer:
No heat is absorbed by the system from the surroundings but work (w) is done on the system. It is adiabatic change. Hence the wall is called adiabatic wall.
![]()
Question 18.
No work is done on the system, but heat (q) is taken out from the system by the surroundings. What type of wall does the system have ?
Answer:
No work is done on the system, but heat (q) is taken out from the system by the surroundings. Then the containing wall is thermally conducting wall.
Question 19.
q = w = -Pext (vf – vi) is for irreversible ………… change.
Answer:
q = w = -Pext (vf – Vi) is for irreversible isothermal change.
Question 20.
q = -w = nRT in (vf/vi) is for isothermal change.
Answer:
q = -w = nRT/n \(\frac{v_f}{v_i}\) is for isothermal reversible change.
Question 21.
What are the ‘∆H’ sign conventions for exothermic and endothermic reactions ? [T.S. Mar. ’16]
Answer:
Compounds which liberate heat in their formation reaction from the constituent elements are called exothermic compounds.
For this reactions, ∆Hf = negative
Compounds which absorb heat in the formation reaction from the constituent elements are called endothermic compounds.
For this reactions, ∆Hf = positive.
Question 22.
What are intensive and extensive properties ?
Answer:
Measurable (or) macroscopic properties such as mass, pressure, volume, temperature, surface tension, viscosity etc., can be subdivided into two categories as below :
i) Extensive properties : The properties whose magnitude depends upon the quantity of matter present in the system are called extensive properties. Examples of such properties are mass, volume, heat capacity, internal energy, entropy, heat content, Gibbs free energy etc. These properties change with quantity of matter present in the system. These properties are additive in nature.
ii) Intensive properties : The properties which do not depend upon the quantity of matter present in the system are called intensive properties. Examples of such properties are density, molar volume, molar entropy, molar heat capacity, surface tension, viscosity, specific heat, refractive index, pressure, temperature, boiling point, freezing point, vapour pressure etc. These properties depends only on the nature of the substance.
![]()
Question 23.
In the equation q = c. m. ∆T. If ∆T is change in temperature’m1 mass of the substance and ‘q1 is heat required, what is ‘c’ ?
Answer:
Given q = c × m × ∆T.
In the above equation c = Specific heat.
Specific heat: The amount of heat required to raise the temperature of 1gm of substance by 1°C is called specific heat.
Question 24.
Give the equation that gives the relationship between ∆U and ∆H.
Answer:
The equation that gives the relationship between ∆U and ∆H.
∆H = ∆U + ∆nRT
∆H = Change in Enthalpy
∆U = Change in Internal energy
∆n = nP – nR, R = Universal gas constant :
T = Temperature
Question 25.
What is the relationship between Cp and Cv ?
Answer:
Cp – Cv = R
Cp = Heat capacity at constant pressure
Cv = Heat capacity at constant volume
R = Universal gas constant.
Question 26.
1g of graphite is burnt in a bomb calorimeter in excess of O2 at 298K and 1 atm. pressure according to the equation.
C(graphite) + O2(g) → CO2(g)
During the reaction the temperature rises from 298K to 299K. Hat capacity of the bomb calorimeter is 20.7kJK-1. What is the enthalpy change for the above reaction at 298 K and 1 atm ?
Answer:
Given equation C(graphite) + O2(g) → CO2(g)
∆T = 299 – 298 = 1K
q = Cv × ∆T = -20.7 × 1 = -20.7 KJ
Given 1 gm of graphite ∴ ∆H = ∆U (∵ ∆h = 0)
∴ ∆U = – 20.7 KJ/k
For 1 mole
∆U = 12 × -20.7 = -248 KJ/mole
![]()
Question 27.
For the above reaction what is the internal energy change, ∆U ?
Answer:
For the above reactions
Internal Energy change ∆U = – 20.7 KJ/k
Question 28.
What is ∆rH for CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) interms of molar enthalpies of the respective reactants and products ?
Answer:
∆rH = Sum of enthalpies of products – sum of enthalpies of reactants
= ∆Hp – ∆Hr
∆rH = (H(CO2) + 2 × H(H2O)) – (H(CH4) + 2 × H(O2))
Question 29.
Enthalpy decrease is not the criterion for spontaneity. Why ?
Answer:
Change in enthalpy “(∆H) = negative” may be a condition but not a necessary and sufficient condition for the spontaneous nature of a reaction.
Question 30.
Is increase of entropy the criterion for spontaneity ? Why ?
Answer:
Change in entropy “(∆S) = positive” is a condition but is not necessary and sufficient condition for the spontaneous nature of a reaction.
Question 31.
Explain the relationship between Gibbs energy change and equilibrium constant.
Answer:
∆G° =2.303 RT logk
∆G = Change in Gibbs free energy
K = Equilibrium constant
![]()
Question 32.
If we measure ∆Hθ and ∆Sθ it is possible to estimate ∆Gθ. Is it true ? why ?
Answer:
∆G° = ∆H° – T ∆S°
If we can measure ∆H° and ∆°S° then we can estimate ∆G° by the above equation, the given statement is true.
Question 33.
Equilibrium constant ‘K’ is measured accurately in the laboratory at given temperature. Is it possible to calculate ∆G° at any other temperature ? How ?
Answer:
It is possible to calculate ∆G° from the measurement of ∆H° and ∆S° and we can calculate K at any temperature.
∆G° = ∆H° – T ∆S°
Question 34.
Comment on the thermodynamic stability of NO(g) given that
\(\frac{1}{2}\) N2(g) + \(\frac{1}{2}\) O2(g) → NO(g); ∆rH° = 90kJ mol-1
NO(g) + \(\frac{1}{2}\) O2(g) → NO2(g); ∆rH° = -74kJ mol-1
Answer:
\(\frac{1}{2}\) N2(g) + \(\frac{1}{2}\) O2(g) → NO(g); ∆rH° = 90kJ mol-1
NO(g) + \(\frac{1}{2}\) O2(g) → NO2(g); ∆rH° = -74kJ mol-1
NO(g) formation is endothermic (∆H = + ve)
NO2(g) formation is exothermic (∆H = -ve)
∴ NO(g) is thermodynamically unstable.
Question 35.
Calculate the entropy change in surroundings when 1.00 mole of H2O(1) is formed under standard conditions ∆fH° = – 286k J mol-1.
Answer:
Formula ∆S = \(\frac{\Delta_{\mathrm{f}} \mathrm{H}^{\circ}}{\mathrm{T}}=\frac{-286}{273}\) = -1.0476 KJ/mole.K
∆Ssurrounding = 1.0476 KJ/mole.k
![]()
Question 36.
The equilibrium constant for a reaction is 10. What will be value of ∆G°? R = 8.314JK-1 mol-1,T = 300K.
Answer:
Formulae ∆G° = —RTlnk
K = 10
R = 8.314 J/K.mole
T = 300 K
= – 2.303 RT logK
= – 2.303 × 8.314 × 300 × log 10 = – 5774.14 J/mole
Question 37.
State the third law of thermodynamics. [T.S. Mar. 16]
Answer:
Third law of thermodynamics: “The entropy of a pure and perfectly crystalline substance is zero at the absolute zero of a temperature (- 273° C)”.
Slim T → 0 = 0
This law imposes a limitation on the value of entropy.
ST = \(\int_0^T \frac{C_p}{T} \cdot d T\)
Short Answer Questions
Question 1.
What are open, closed and isolated systems ? Give one example for each.
Answer:
Types of systems : The systems are classified into three types. These are :
a) Open system : A system which can exchange matter as well as energy with the surroundings is called an open system.
Ex :Evaporation of water from a beaker presents as open system.
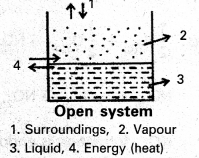
Here vapours of water (matter) go into the atmosphere and heat (energy) required is absorbed by water from the surroundings.
b) Closed system : A system which may exchange energy but not matter with surroundings is called a closed system.
Ex : Consider boiling of water in a closed metallic vessel. Here, heat is transferred from the burner (surroundings) to the system. Steam remains inside the vessel. Thus, matter is not exchanged.
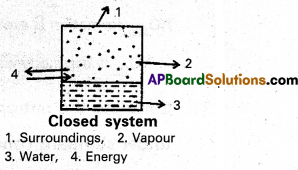
c) Isolated system : A system which can neither exchange matter nor energy with the surroundings is called an isolated system.
Ex : Take some water in an insulated vessel and put a small piece of sodium metal in it. An exothermic reaction takes place.
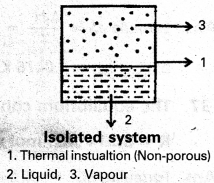
Neither hydrogen gas (matter) nor heat (energy) is transferred to the surroundings.
![]()
Question 2.
Define the state function and state variables, Give examples.
Answer:
State function : Properties of the systems which depends on the initial and the final states of the system but are independent of the path are called state functions.
Eg. : Energy, Volume, Enthalpy, Gibbs Energy.
State variables : Variables like P, V, T are called state variables. These are used to describe a system completely.
Question 3.
“Internal energy is a state function”. Explain.
Answer:
Internal energy (E) : ‘The total energy stored in the substance at constant temperature and pres-sure is called its internal energy (E)”.
It is a state function and is an extensive property.
Internal energy change (∆E) is considered as the difference between the internal energies of products and reactants.
∆E = (Ep – Er)
In any path taken (Q – W) is equal to ∆E.
Where Q = heat and W = Work.
Internal energy is a state function it depends on initial state and find state of the system.
Question 4.
“Work is not a state function”. Explain.
Answer:
Work is not a state function.
- One state of a system can be changed to another in a several ways. Work involved in different paths differ in their quantity.
- Work depends on the path of the reaction but not on the state of the system.
- Work is dependent on the capacity factor and intensity factor.
![]()
Question 5.
What is heat ? Explain.
Answer:
The internal energy of a system can be change by transfer of heat from the surroundings to system (or) vice versa with out consumption of work.
This exchange of energy which results of temperature difference is called heat (q).
Question 6.
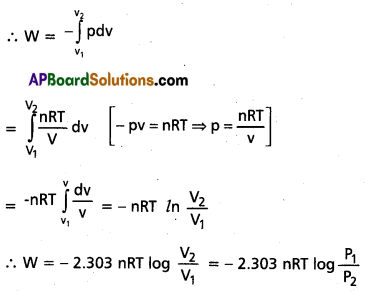
Derive the equation for ‘Wrev‘ in isothermal reversible process.
Answer:
Derivation of equation for Wrev in isothermal reversible process :
Let the work done against the pressure Sw = -P.dv
Assume that expansion isothermally from volume V1 to volume V2
[P = pressure (External)
dv = change in volume]
Question 7.
Two litres of an ideal gas at a pressure of 10 atm expands isothermally into a vacuum until its total volume is 20 litres. How much heat is absorbed and how much work is done in the expansion ?
Answer:
Heat absorbed = 0
‘P‘ of gas = 10 at m
PExp = 0
V1 = 2 lit
V2 = 20 lit
Because the given process is isothermal
∴ ∆U = 0
q + w = 0
q = -w
= pex (V2 – V2)
= Pex(20 – 2) = 0
= 0 (18) = 0
q = 0 and work done also zero
∴ w = 0
![]()
Question 8.
If the ideal gas given in the problem 45 expands against constant external pressure of 1 atm what is the q value ?
Answer:
Formula
q = – W
pex = 1 atm
pgas = 10 atm
V1 = 2 lit
V2 = 20 lit
= pex(VV2 – V2)
= 1 (20 – 2)
= 18 lit. atm
Question 9.
If the ideal gas given in the problem 45 expands to a final volume of 10L conducted reversibly what is q value ?
Answer:
V1 = 2 lit, V2 = 10 lit.
The expression for reversible isothermal expansion; q = 2.303 log \(\frac{\mathrm{v_2}}{\mathrm{v_1}}\)
q = -w = 2.303 × log \(\frac{20}{2}\) = 2.303 × 20 log 10
= 46.06 lit. atm.
Question 10.
Explain the state function enthalpy, H’. What is the relationship between ∆U and ∆H ?
Answer:
Enthalpy (H) : “Enthalpy is the amount of heat exchanged by a system with its surroundings at constant pressure and temperature”.
The energy change taking place at constant pressure and at a constant temperature is called enthalpy change (∆H).
Mathematically, ∆H = ∆U + P. ∆N. When ∆U = Internal energy change.
Enthalpy is state function. Thus, the magnitude of enthalpy change depends only upon the enthalpies in the initial and the final states.
∆H = [HProducts – HReactants]
For gaseous reactions, ∆H = ∆U + ∆nRT
![]()
Question 11.
Show that ∆H = ∆U + ∆n(g), RT
Answer:
The energy change taking place at constant pressure and at a constant temperature is called enthalpy change (∆H).
Mathematically, ∆H = ∆U + P. ∆V. When ∆U = Internal energy change.
Enthalpy is state function. Thus, the magnitude of enthalpy change depends only upon the enthalpies in the initial and the final states.
∆H = [HProducts – Hreactants]
For gaseous reaction, ∆H = ∆U + ∆nRT
Consider PV1 = n1 RT
PV2 = n2 RT
PV2 – PV1 = n2 RT – n1 RT
P(V2 – V1) = (n2 – n11)RT
P × ∆V = ∆ ng RT
[We know that ∆H = ∆U + P∆V]
∆H = ∆U + ∆ng RT
Question 12.
If Water vapour is assumed to be a perfect gas, molar enthalpy change for vapourisation of 1 mole of water at 1 bar and 100° C is 41 kJ mol-1. Calculate the internal energy change when
a) 1 mol of water is vapourised at 1 bar and 100° C
b) 1 mol of water liquid is converted into ice.
Answer:
∆H = 41kJ
∆ng = 1
a) H2O ⇌ H2O(g)
∆H = ∆U + ∆n(g) RT
41 = ∆U + 8.314 × 10-3 × 373
∆U = 41 – 3.101 = 37.899 KJ / mole
b) H2O ⇌ H2O(ice)
∆H = ∆U + ∆n(g) RT
∆H = ∆U [∵ ∆n = 0]
∆H = ∆U = 41 kJ /mole
![]()
Question 13.
Explain extensive and intensive properties.
Answer:
Measurable (or) macroscopic properties such as mass, pressure, volume, temperature, surface tension, viscosity etc., can be subdivided into two categories as below :
i) Extensive properties: The properties whose magnitude depends upon the quantity of matter present in the system are called extensive properties. Examples of such properties are mass, volume, heat capacity, internal energy, entropy, heat content, Gibbs free energy etc. These properties change with quantity of matter present in the system. These properties are additive in nature.
ii) Intensive properties: The properties which do not depend upon the quantity of matter present in the system are called intensive properties. Examples of such properties are density, molar volume, molar entropy, molar heat capacity, surface tension, viscosity, specific heat, refractive index, pressure, temperature, boiling point, freezing point, vapour pressure etc. These properties depends only on the nature of the substance.
Question 14.
Define heat capacity. What are Cp and Cv ? Show that Cp – Cv = R.
Answer:
Heat capacity (C) : “Heat capacity (G) of a substance is defined as the amount of heat required to raise its temperature through one degree”.
(or)
It is the ratio of heat absorbed (q) to the resulting increase in temperature (dT)
∴ C = \(\frac{\mathrm{q}}{\mathrm{dT}}\)
Heat capacity (C) is a state function. Hence to evaluate ‘C’, the conditions such as volume or constant pressure have to be specified in order to define the path. Thus there are two different types of heat capacities. These are :
i) Heat capacity at constant volume (Cv)
ii) Heat capacity at constant pressure (Cp).
From first law of thermodynamicsl,
q = dE + W = dE + P.dV (∵ W = PV)
∴ C = \(\frac{\mathrm{q}}{\mathrm{dT}}\) = \(\frac{\mathrm{dE}+\mathrm{P} \cdot \mathrm{dV}}{\mathrm{dT}}\)
If the absorption of heat takes place at constant volume, Cv (i.e.,) dV = 0
∴ Cv = \(\frac{\mathrm{q}_{\mathrm{V}}}{\mathrm{dT}}=\frac{\partial \mathrm{E}+\mathrm{O}}{\partial \mathrm{T}}=\left(\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right)_V\)
∴ Cv = \(\left(\frac{\partial E}{\partial T}\right)_V\)
Definition for “Cv“: Heat capacity of a system at constant volume (Cv) may be defined as rate of change of internal energy with temperature at constant volume.
If heat is absorbed by the system at constant pressure, heat capacity is denoted by ‘Cp‘ and is called heat capacity at constant pressure.
Cp = \(\frac{\mathrm{q}_{\mathrm{p}}}{\mathrm{dT}}=\left(\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right)_{\mathrm{p}}+\mathrm{P}\left(\frac{\partial \mathrm{V}}{\partial \mathrm{T}}\right)_{\mathrm{p}}\) ………… (1)
But H = E + PV
Differentiating this equation w.r.to T at constant pressure, we get
\(\left(\frac{\partial \mathrm{H}}{\partial \mathrm{T}}\right)_p=\left(\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right)_p+\left(\frac{\partial \mathrm{V}}{\partial \mathrm{T}}\right)_p\) ………………. (2)
From equation (1) and (2), we get
Cp = \(\left(\frac{\partial \mathrm{H}}{\partial \mathrm{T}}\right)_p\)
Definition for Cp: Heat capacity of a system at constant pressure (Cp) may be defined as rate of change of enthalpy with temperature at constant pressure.
Derivation of Cp – Cv = R
H = E + PV (For an ideal gas)
differentiating w.r.t. T.
\(\frac{\mathrm{dH}}{\mathrm{dT}}=\frac{\mathrm{dE}}{\mathrm{dT}}+\frac{\mathrm{d}(\mathrm{PV})}{\mathrm{dT}}\)
⇒ \(\frac{\mathrm{dH}}{\mathrm{dT}}=\frac{\mathrm{dE}}{\mathrm{dT}}+\frac{\mathrm{d}(\mathrm{RT})}{\mathrm{dT}}\) [∵ PV = RT]
\(\frac{\mathrm{dH}}{\mathrm{dT}}=\frac{\mathrm{dE}}{\mathrm{dT}}+\mathrm{R}\)
Cp – Cv = R
![]()
Question 15.
Explain the determination of ‘∆U’ of a reaction calorimetric
Answer:
- The technique of measuring heats of reactions is called calorimetres. The apparatus used is calorimeter.
- Calorimeter is a vessel properly insulated and contains water as the calorimetric liquids.
- A combustioble substance is burnt in oxygen.
- Heat evolved during the reaction is measured from the rise in temperature.
- Here there is no worke done as ∆V = 0
- By the raise of temperature of water bath and calorimeter the amount of heat evolved can be determined.
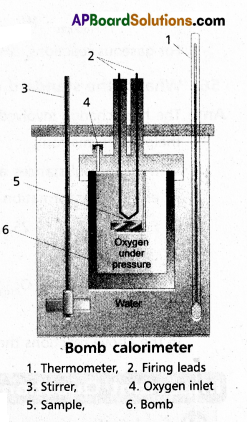
Internal Enegy ∆U = Q. ∆t × \(\frac{M}{m}\)
Q = heat capacity
∆t = t2 – t1
M = molar mass of substance
m = mass of the substance
Question 16.
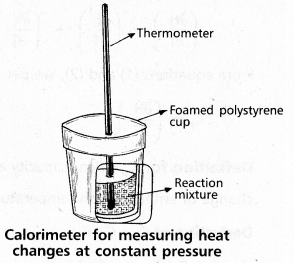
Explain the determination of ∆H of a reaction calorimetrically.
Answer:
Heat change at constant pressure can be measured in a calorimeter at constant pressure ∆H = qp
∴ For Exothermic reaction ∆H = -ve
For Endothermic reaction ∆H = +ve
Question 17.
What is enthalpy of a reaction ? Explain the standard enthalpy of a reaction.
Answer:
Enthalpy (H) : “Enthalpy is the amount of heat exchanged by a system with its surroundings at constant pressure and temperature”.
The energy change taking place at constant pressure and at a constant temperature is called enthalpy change (∆H).
Mathematically, ∆H = ∆U + P. ∆V. When ∆U = Internal energy change.
Enthalpy is state function. Thus, the magnitude of enthalpy change depends only upon the enthalpies in the initial and the final states.
∆H = [HProducts – HReactants]
For gaseous reactions, ∆H = ∆U + ∆nRT
![]()
Question 18.
What is the standard enthalpy of formation ? Explain it with example.
Answer:
The heat change involved in the reaction of formation of one mole of a compound is called enthalpy of formation.
If all the substances are in the standard states the enthalpy of formation is called standard enthalpy of formation.
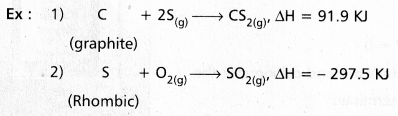
In the above reactions the substances are in standand states
Question 19.
Define and explain enthalpy of phase transformation.
Answer:
Enthalpy of phase transformation : The heat change involved in the change of phase (or) physical state of one mole of compound at atmospheric pressure.
a) Standard molar enthalpy of fusion (∆fusH0) : The enthalpy change that accompanies melting of one mole of a soild substance in standard state is called Standard molar enthalpy of fusion.
Eg : H2O(s) → H2O(l) ∆fusH0 = 6.00 KJ mol-1
b) Standard molar enthalpy of vapourisation (∆vapH0): Amount of heat required to vapourise 1 mole of a liquid at constant temperature and under standard pressure (1 bar) is called its standard molar enthalpy of vapourisation (∆vapH0).
Eg : H2O(l) → H2O(g) ∆vapH0 = + 40.79 KJ mol-1
c) Standard enthalpy of sublimation (∆subH0): It is the change in the enthalpy when are mole of a solid substance sublimes at a constant temperature under standard pressure.
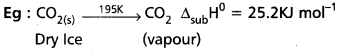
Question 20.
Define and explain the standard enthalpy of vapourisation (Molar enthalpy of vapourisation)
Answer:
Standard molar enthalpy of fusion (∆fusH0) : The enthalpy change that accompanies melting of one mole of a soild substance in standard state is called Standard molar enthalpy of fusion.
Eg : H2O(s) → H2O(l) ∆fusH0 = 6.00 KJ mol-1
Question 21.
Define and explain the standard enthalpy of vapourisation (Molar entghalpy of vapourisation)
Answer:
Standard molar enthalpy of vapourisation (∆vapH0) : Amount of heat required to vapourise 1 mole of a liquid at constant temperature and under standard pressure (1 bar) is called its standard molar enthalpy of vapourisation (∆vapH0).
Eg : H2O(l) → H2O(g) ∆vapH0 = + 40.79 KJ mol-1
![]()
Question 22.
Define and explain the standard enthalpy sumlimation.
Answer:
Standard enthalpy of sublimation ∆subH0 : It is the change in the enthalpy when are mole of a solid substance sublimes at a constant temperature under standard pressure.
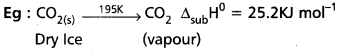
Question 23.
Define and explain the standard enthalpy of formation (∆f Hθ).
Answer:
The heat change involved in the reaction of formation of one mole of a compound is called Enthalpy of formation
If all the substances are in the standard states the enthalpy of formation is called standard enthalpy of formation.
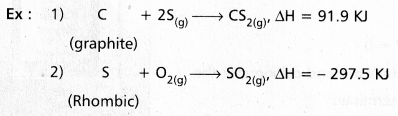
Question 24.
State and explain the Hess’s law of constant Heat summation. [Mar. ’13]
Answer:
Hess’s law states that the total amount of heat evolved or absorbed in a chemical reaction is always same whether the reaction is carried out in one step (or) in several steps.
Illustration : This means that the heat of reaction depends only on the initial and final stages and not on the intermediate stages through which the reaction is carried out. Let us consider a reaction in which A gives D. The reaction is brought out in one step and let the heat of reaction be ∆H.
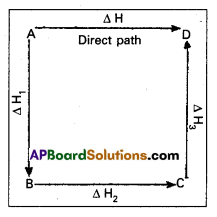
A → D; ∆H
Suppose the same reaction is brought out in three stages as follows :
A → B : ∆H1
B → C : ∆H2
C → D : ∆H3
The net heat of reaction is ∆H1 + ∆H2+ ∆H3.
According to Hess law ∆H = ∆H1 + ∆H2 + ∆H3.
Ex : Consider the formation of CO2. It can be prepared in two ways.
1) Direct method : By heating carbon in excess of 02.
C(s) + O2(g) → CO2(g); ∆H = – 393.5 kJ
2) Indirect method : Carbon can be converted into CO2 in the following two steps.
C(s) + \(\frac{1}{2}\)O2(g) → CO2(g); ∆H1 = – 110.5 kJ
CO (g) + \(\frac{1}{2}\) O2(g) → CO2(g); ∆H2 = – 283.02 kJ
Total ∆H = -393.52 kJ (∆H1 + ∆H2)
The two ∆H values are same.
![]()
Question 25.
Define and exlain the enthalpy of combustion (∆cHθ).
Answer:
Standard enthalpy of combustion is defined as the enthalpy change per mole (or per unit amount) of a substance, when it undergoes combustion and all the reactants and products being in their standard states at the specified temperature.
Cooking gas in cylinders contains mostly butane (C4 H10). During complete combustion of one mole of butane, 2658 kJ of heat is released. We can write the thermochemical reactions ofr this as :
C4 H10 (g) + \(\frac{13}{2}\) O2 (g) → 4CO2 (g) + 5H2O(1);
∆cHθ = -2658.0 kJ mol-1
Question 26.
Define and explain enthalpy of atomisation (∆aHθ).
Answer:
- The heat required to dissociate 1 mole of a simple molecule in the gaseous state into its constituent atoms.
- This is an endothermic process.
Ex: O2(g) → 2O(g) ∆H = 489.5 KJ
N2(g) → 2N(g) ∆H = 937.4 KJ
Question 27.
Define and explain the Bond enthalpy (∆bondHθ)
Answer:
Bond Enthalpy : The change in enthalpy when one mole of covalent bonds of a gaseous covalent compond is broken to from gaseous products is called Bond dissociation Enthalpy.
Ex : H2(g) → 2H(g) ∆H = 435.9 KJ / mole
Question 28.
What is the bond enthalpy of C-H bond of CH4 ?
Answer:
The bond dissociation enthalpy for step wise dissociation of CH4 molecule are CH.
CH4(g) → CH3(g) + H(g) ; ∆ H0 = 427.0 kJ
CH3(g) → CH2(g) + H(g) ; ∆ H0 = 418.4kJ
CH2(g) → CH(g) + H(g) ; ∆ H0 = 460.2 kJ
CH(g) → C(g) + H(g) ; ∆ H0 343.1 kJ
The enthalpy for each step is different due to the reason that in each step of dissociation different fragments of CH4 are involved.
But the average bond dissociation enthalpy is 1/4 of the total energy required to break one mole of CH4 into C(g) + 4H (g).
C-H bond dissociation Enthalpy = \(\frac{427.0+418.4+460.2+343.1}{4}\)
= \(\frac{1648.7}{4}\) = 412.2 kJ
![]()
Question 29.
Define heat of solution (∆solHθ) and heat of dilution.
Answer:
i) Enthalpy of solution : Definition : The amount of heat evolved or absorbed when 1 mole of a solute is dissolved completely in large excess of solvent is called Enthalpy of solution.
(Or)
The change of enthalpy when a solution containing 1 mole of a solute is diluted from one concentration to another.
Ex : KCl (s) + aq → KCl (aq), DH = + 19.75 kJ
This is measured per mole of solute. If solvent is water then it is called enthalpy of dilution.
ii) Enthalpy of dilution : The change of enthalpy when a solution containing 1 mole of a solute is diluted from one concentration to another.
Ex : HCl (g) + aq → HCl (aq), ∆H = – 75.4 kJ
Question 30.
Define ionisation enthalpy and electron affinity.
Answer:
Ionisation Enthalpy : The enthalpy change observed by the removal of an electron from the neutral isolated gaseous atom is called ionisation enthalpy.
![]()
Electron affinity : The enthalpy evolved by the addition of electron to neutral gaseous atom is called electron affinity.
X(g) + e– → X–(g) + EA
Observe the following spontaneous reactions
1) H2(g) + 1/2 O2(g) H2O = -285.8 kJ / mole
2) c(graphite) + 2S(g) → CS2(g) ∆ H0 = 91.91 kJ / mole
In reaction (1) ∆H = -ve, in reaction (2) ∆H = +ve
∴ The decrease in Enthalpy may be a condition but not a necessary and sufficient condition for spontaneity of a reaction.
Ionization Energy and Electron Affinity : Ionization energy and electron affinity are defined at absolute zero. At any other temperature, heat capacities for the reactants and the products have to be taken into account. Enthalpies of reactions for
M(g) → M+(g) + e– (for ionization)
M(g) + e– → M–(g) (for electron gain) at temperature, T is
∆rHΘ(T) = ∆rHΘ(0) + \(\int_0^T \Delta_r C_p^{\Theta} d t\)
The value of Cp for each species in the above reaction is 5/2 R (Cv = 3/2R)
So, ∆rCpΘ = 5/2 R (for ionization)
∆rCpΘ = -5/2 R (for electron gain)
Therefore,
∆rHΘ = (Ionization enthalpy)
= E0 (ionization energy) + 5/2 RT
∆rHΘ = (electron gain enthalpy)
= -A (electron affinity) = 5/2 RT
![]()
Question 31.
Explain the spontaneity of a process.
Answer:
Spontaneous reaction :
A process is said to be spontaneous if it occurs on its own without intervention of any external agency of any kind.
All natural processes are spontaneous.
Entropy increases in all spontaneous processes.
Change in entropy “(∆S) = positive” is a condition but is not necessary and sufficient condition for the spontaneous nature of a reaction.
Change in enthalpy “(∆H) = negative” may be a condition but not a necessary and sufficient condition for the spontaneous nature of a reaction.
At this juncture, “Gibbs” introduced another thermodynamic function which involves both enthalpy (H) and entropy (S) functions. This is known as free energy function (G). This is given by the equation.
G = H – TS. .’G1 is now referred as ‘Gibbs energy (or) Gibbs function.
“∆Gsys is negative” for spontaneous reactions (or) processes. Thus the spontaneity of a reaction and the algebraic signs of ∆H, ∆S, ∆G and the magnitude of T can be related as follows :

Question 32.
Is decrease in enthaply a crieterion for spontaneity ? Explain. [A.P. Mar. 16]
Answer:
Change in enthalpy “(∆H) = negative” may be a condition but not a necessary and sufficient condition for the spontaneous nature of a reaction. ;
Observe the following spontaneous reactions
- H2(g) + 1/2 O2(g) ⇌ H2O ∆ H0 = -285.8 kJ/mole
- C(graphite) + 2S(g) → CS2(g) ∆ H0 = 91.91 kJ/mole
In reaction (1) ∆H = -ve, in reaction (2) ∆H = +ve
∴ The decrease in enthalpy may be a condition but not a necessary and sufficient condition for spontaneity of reaction.
Question 33.
What is entropy ? Explain with examples.
OR
Explain “Entropy” concept.
Answer:
Entropy (S): Entropy is taken as a measure of disorder of molecules (or) randomness of the system. Greater the disorder of molecules in a system, the higher is the entropy. Entropy is a state function. It depends on the temperature, pressure of the state.
Entropy change, ∆S = \(\frac{\mathrm{q}_{\mathrm{rev}}}{\mathrm{T}}\) [qrev = heat absorbed by the system isothermally and reversibly at T]
For a spontaneous process in an isolated system the entropy change is positive.
(∆S = positive)
∆Stotal = ∆Ssystem + ∆Ssurroundings

![]()
Question 34.
Is increase in entropy a criterion for spontaneity ? Explain.
Answer:
Change in entropy “(∆S) = positive” is a condition but is not necessary and sufficient condition for the spontaneous nature of a reaction.
For a spontaneous process change in entropy is positive
∆S = +ve (spontaneous)
∆S = -ve (backward reaction is spontaneous)
∆S = 0 (Equilibrium reaction)
∴ ∆H = -ve, ∆S = +ve, ∆G = -ve then the reaction
Spontaneous at all T values (Reaction is irreversible)
Question 35.
Can All and ∆S discriminate between irreversible and reversible processes ? Explain.
Answer:
- Change in internal energy (∆U)
- In exothermic process and internal energy lowered (Reaction is Spontaneous)
- In case of reversible reaction the reaction favoured in the direction where there is decrease in the internal energy.
Change in entropy “(∆S) = positive” is a condition but is not necessary and sufficient condition for the spontaneous nature of a reaction.
For a spontaneous process change in entropy is positive
∆S = +ve (spontaneous)
∆S = -ve (backward reaction is spontaneous)
∆S = 0 (Equilibrium reaction)
∴ ∆H = -ve, AS = +ve, ∆G = -ve then the reaction
Spontaneous at all T values (Reaction is irreversible)
Question 36.
In which of the following processes entropy increases ?
a) A liquid evaporates to vapour.
b) Temperature of a crystalline solid lowered from 115K to OK
c) CaCO3(s) → CaO(s) + CO2(g)
d) Cl2(g) → 2Cl(g)
Answer:
a) When a liquid evaporates to vapour randomness increases in the vapour state ∆S is +ve. Hence the process is spontaneous.
b) If the temperature of the crystalline solid is lowered to OK it becomes perfectly ordered. No disorder is noticed. Hence such a process is not spontaneous.
c) CaCO3(s) → CaO(s) + CO2(g)
∆S is very slightly positive. If temp is increased ΔS becomes more positive.
d) Cl2(g) → 2Cl(g)
It is an endothermic process there is no considerable increase in entropy. The process is not spontaneous.
![]()
Question 37.
For the oxidation of iron
4Fe(s) + 3O2(g) → 2Fe(2)O3(s), the entropy change is -549.45JK-1 mol-1 at 298K. Though it has negative entropy change the reaction is spontaneous. Why ?
(∆rHΘ = -1648 × 103 J mol-1)
Answer:
One decides the spontaneity of a reaction by considering
∆Stotal i.e< (∆Ssys + ∆Ssurr). For calculating ∆Ssurr, we have to consider the heat absorbed by the surroundings which is equal to -∆rHΘ. At temperature T, entropy change of the surroundings is
∆Ssurr = \(\frac{\Delta_{\mathrm{r}} \mathrm{H}^\theta}{\mathrm{T}}\) (at constant pressure)
= \(-\frac{\left(-1648 \times 10^3 \mathrm{Jmol}^{-1}\right.}{298 \mathrm{~K}}\) = 5530 JK-1 mol-1
Thus, total entropy change for this reaction
∆rStotal = 5530 JK-1 mol-1 + (-549.4 JK-1 mol-1) = 4980.6 JK-1 mol-1
This shows that the above reaction is spontaneous.
Question 38.
Which formalae in the following are correct ?
a) G = H – TS
b) ∆Gsys = ∆Hsys = ∆Hsys – ∆Ssys
c) ∆Ssurr = \(\frac{\Delta H_{\text {sur }}}{T}=\frac{-\Delta H_{\text {sys }}}{T}\)
d) ∆Ssurr = ∆Hsys + \(\frac{-\Delta \mathrm{H}_{\text {sys }}}{T}\)
e) TASTotal = T∆Hsys – ∆Hsys
Answer:
a) Correct
b) Correct at constant temperature
c) Correct
d) Correct
e) Not correct
Question 39.
Calculate ∆rGθ for conversion of oxygen to ozone ∆rGθ=163 kJ mol-1 O2(g) → O3(g) at 298K. Kp for the \(\frac{3}{2}\) the reaction is 2.43 × 10-29
Answer:
∆G0 = -2.303 RT log Kp
= -2.303 × 8.314 × 298 × log 2.43 × 10-29
= -16300 J/mole
= 163 kJ/mole
![]()
Question 40.
State the second law of thermodynamics and explain it.
Answer:
II law of thermodynamics :
Statements :
- “It is impossible for a self acting machine unaided by any external agency to convert heat from a body at low temperature to a body at higher temperature”.
- “All spontaneous processes are thermodynamically irreversible and entropy of the system increases in all spontaneous processes.”
- “For any spontaneous process taking place in an isolated system, the change in entropy (∆S) is positive.”
Question 41.
State the third law of thermodynamics. What do you understand by it ?
Answer:
Third law of thermodynamics: “The entropy of a pure and perfectly crystalline substance is zero ; at .the absolute zero of a temperature (-273° C)”.
Slim T → 0 = 0
This law imposes a limitation on the value of entropy.
ST = \(\int_0^T \frac{C_p}{T} \cdot d T\)
Thus entropy (S) of a substance at any temperature is calculated if the temperature dependence of ‘Cp‘ is known in evaluating absolute entropy of any substance.
Importance of this law : One of the most important applications of third law is the calculation of entropy changes in chemical reactions.
Question 42.
Explain spontaneity of a process in terms of Gibbs energy.
Answer:
∆G = ∆H – T∆S
∆Gsys = negative for spontaneous reactions (∆G < 0)
∆Gsys = positive for non – spontaneous reactions (∆G > 0)
∆Gsys = zero for equilibrium reactions (∆G = 0)
∆G =-ve, ∆S =+ve, ∆H =-ve are the conditions for the sponaneity of reaction.
Question 43.
The sign and magnitude of Gibbs energy change of a chemical process tells about its spontaneity and useful work that could be extracted from it. Explain.
Answer:
To predict about the spontaneity of the reaction and
To redict the useful work that could be extract is the sign and magnitude of the quantities in Gibb’s equation is useful.
When a reaction is reversible it cannot proceed in both the direction with same case. In general the system would spontaneously change to configuration of lower free energy.
At equilibrium ∆G = 0
0 = ∆G° + RTLnK
∆rG° = -RTLnK = -2.303 RT log k
We know ∆rG° = ∆rH° – T∆rS° = -RT log k
For endothermic reaction ∆rH° may be large and positive
In such a case K is much less (K < 1)
In exothermic reactions ∆rH° is large and negative (K >1)
∴ For exothermic reaction
a) K must be large
b) ∆rG° is highly negative
c) ∆S° is highly positive
Hence with the sign and magnitude of the factors the yield of the product may be estimated.
![]()
Question 44.
In a process 701 J of heat is absorbed by a system and 394J of work is done by the system. What is the change in internal energy for the process ?
Answer:
q = 701 J
w = -394 J
∆U = q + w
∆U = 701 – 394
= 307 J
Question 45.
The reaction of cyanamide (s). with dioxygen was carried out in a bomb calorimeter and ∆U was found to be – 742, 7kJ mol-1 at 298K. Calculate the enthalpy change for the reaction at 298k.
NH2CN(g) + \(\frac{3}{2}\) O2(g) → N2(g) + H2O(1)
Answer:
NH2CN(g) + \(\frac{3}{2}\) O2(g) → N2(g) + H2O(1)
∆n = 2 – \(\frac{5}{2}\)
= 0.5
∆U = – 742 kJ/mol
∆H = ∆U + ∆n RT
∆H = – 742 + (-0.5) × 8.314 × 10-3 × 298
= -742.7 – 1.238
= – 743.94 kJ/mol4.
Question 46.
Calculate the number of kJ of heat necessary to rise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of aluminimum is 24 J mol-1 K-1.
Answer:
Given molar heat capacity of Al = 24 J/mole.k
= \(\frac{24}{27}\) J/gm. k
The heat necessary to raise the temp, of 60 g. of Al from 35°C to 55°C
= 60 × \(\frac{24}{27}\) × 55 – 35
= 60 × \(\frac{24}{27}\) × 20 = 1.067 kJ
Question 47.
Calculate the enthalpy change on freezing of 1.0 mol of water at 10.0°C to ice at 10.0°C. ∆fus H = 6.03 kJ mol-1 at 0°C.
Cp [H2 O(1)] = 75.3J mol-1 K-1
Cp [H2O(s)] = 36.8 J mol-1 K-1
Answer:

∆Hfus = 6.03 kJ
1 mole of water taken to -10°C from 0°C
∆H = Cp ∆T = 36.8 × -10 = – 3685
= 0.368 kJ.
Total enthalpy = 6.03 + 0.753 – 0.368
= 6.415 kJ/mole.
![]()
Question 48.
Enthalpy of combustion of carbon to CO2 is – 393.5 kJ mol-1. Calculate the heat released upon formation of 35.2 g of CO2 from carbon and dioxygen gas.
Answer:
C(s) + O2(g) → CO2(g) ∆H = -393.5 kJ/mole
44gms of CO2 → -393.5 kJ
35.2 gms of CO2 → ?
\(\frac{35.2 \times 393.5}{44}\) = -314.8 kJ
Question 49.
Enthalpies of formation of CO(g), CO2(g) and N2O4(g) are – 110, -393, 81 and 9.7 kJ mol-1 respectively. Find the value of ∆rH for the reaction :
N2O4(g) + 3CO(g) → N2O(g) + 3CO2(g)
Answer:
N2O4(g) + 3CO(g) → N2O(g) + 3CO2(g)
∆HCO = -110 KJ
∆HCO2 = -393 KJ
∆HN2O = -81 KJ
∆HN2O4 = -9.7 KJ
∆H = sum of enthalpies of products – sum of enthalpies of reactants
= -1017 – (-320.3)
∆H = -696.7kJ
Question 50.
Given N2(g) + 3H2(g) → 2NH3(g); ∆rH° = – 92.4 kJ mol-1 What is the standard enthalpy of formation of NH3 gas ?
Answer:
N2(g) + 3H2(g) → 2NH3(g)
2 moles of NH3 → -92.4kJ
For 1 mole of NH3 → \(\frac{-92.4}{2}\) = -46.2
∆H°(NH3) = -46.2 KJ l mole
![]()
Question 51.
Calculate the standard enthalpy of formation of CH3OH(l) from the following data :
CH3OH(l) + \(\frac{3}{2}\)O2(g) → CO3(g) + 2H3OΘ; ∆rH° = -726 kJ mol-1
C(graphite) + O2(g) → CO2(g); ∆cH° = – 393 kJ mol-1
H2(g) + O2(g) → H2O(l); ∆fH° = -286 kJ -mol-1.
Answer:
Given ∆fH° (CO2) = -393 KJ mol-1
∆fH° (H2O(1)) = -286 KJ mol-1
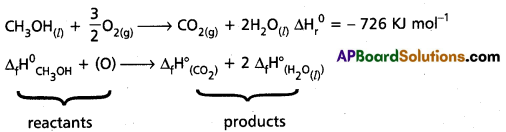
∆rH° = -726 KJ mol-1
∆rH°= ∆H°total total of the products – ∆H°total total of the reactants
-726 = [-393 + 2 (-286)] – [∆fH° CH3OH].
∆rH° (CH3OH) = 726 + [-393 + 2(-286)] KJ mol-1
= – 239 KJ mol-1
Question 52.
Calculate the enthalpy change for the process
CCl4(g) → C(g) + 4 Cl(g)
and calculate bond enthalpy of C – Cl in CCl4(g).
∆vap H°(CCl4) = 30.5 kJ mol-1.
∆fH°(CCl4) = – 135.5 kJ mol-1.
∆aH° (C) = 715.0 kJ mol-1, where ∆aH° is enthalpy of atomisation
∆aH° (Cl2) = 242 kJ mol-1
Answer:
CCl4(1) → CCl4(g) → C(g) + 4Cl(g)
∆vap H°(CCl4) = 30.5 kJ mol-1.
∆fH°(CCl4) = – 135.5 kJ mol-1.
∆H°(C) = 715.0 kJ mol-1
∆rH° (Cl2) = 242 kJ mol-1
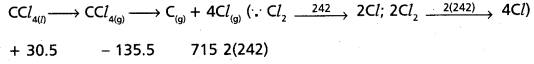
∆rH° = 715 + 484 + 135.5 – 30.5
∆rH° = 1334.5 – 30.5 KJ mol-1 = 1304 KJ
C – Cl bond enthalpy = \(\frac{1304}{4}\) = 326 KJ mol-1
Question 53.
For an isolated system, ∆U = 0, what will be ∆S ?
Answer:
Given an Isolated system
For isolated system ∆U = 0
∴ ∆H = ∆U + ∆nRT
∆H = ∆nRT
∆H = \(\frac{\Delta \mathrm{H}}{\mathrm{T}}=\frac{\Delta \mathrm{nRT}}{\mathrm{T}}\)
∴ ∆S > 0 ∆S = + ve
![]()
Question 54.
For the reaction at 298 K.
2A + B → C
∆H = 400 kJ mol-1 and ∆S = 0.2 kJ K-1 mol-1
At what temperature will be reaction become spontaneous considering ∆H and ∆S to be constant over the temperature range.
Answer:
Formula ∆S = \(\frac{\Delta \mathrm{H}}{\mathrm{T}}\)
T = \(\frac{\Delta \mathrm{H}}{\Delta \mathrm{S}}=\frac{400}{0.2}\) = 2000K
Question 55.
For the reaction, 2 Cl(g) → Cl2(g), what are the signs of ∆H and ∆S ?
Answer:
2 Cl(g) → Cl2(g)
Here in the above reaction chlorine atoms (reactive)
Converted into stable Cl2 molecule It is an exothermic reaction
∆H = – ve, ∆S = + ve
Question 56.
For the reaction 2 A(g) + B(g) → 2D(g)
∆U° = – 10.5 kJ and ∆S° = – 44.1 JK-1.
Calculate ∆G° for the reaction and predict whether the reaction can occur spontaneously or not.
Answer:
2A(g) + B(g) → 2D(g)
ng = 2 – 3 = -1
∆H = ∆v + ng RT
∆H = – 10.5 + (-1) × \(\frac{8.314}{10^3}\) × 298
– 10.5 – 2.477 = – 12.977 KJ mol-1
∆S = -44.1 JK-1
∆G° = ∆H – T∆S
∆G° = – 12.977 – 298 (-44.1)
= – 12977 + 13141.8 = 1648 J or + 0.1648 J
∴ ∆G° is +ve the reaction is non spontaneous.
Question 57.
The equilibrium constant for a reaction is 10. What will be the value of ∆G° ? R = 8.314 JK-1 mol-1, T = 300 K.
Answer:
Formula ∆G° = – RT lnk
∆G° = – 2.303 RT log k
∆G° = – 2.303 × 8.314 × 300 × log 10
= – 5744 J/mole
∆G° = -5.744 KJ/mole
![]()
Question 58.
State the first law of thermodynamics. Explain its mathematical notation.
Answer:
First law of thermodynamics :
The law of conservation of energy is taken as the first law of thermodynamics.
Statements :
- “Energy can neither be created nor destroyed, although it can be transformed from one form to another”.
- “It is impossible to construct a perpetual motion machine of first kind (which produce work without consuming energy)”.
- “The total energy of the system and surroundings is constant”.
Mathematical form :
Let a system in state “A”, of internal energy EA absorb from the surroundings acertain amount of heat (Q) and undergo a change in its state to B. Let the internal energy in the state B is EB. If W is the work done by the system in the process, the increase in internal energy ∆E of the system is given by the equation, ∆E = EB – EA
![]()
From first law, net gain of energy (Q – W) must be equal to ∆E
∆E = (EB – EA) = (Q – W)
(or) Q = ∆E + W For infinitesimally small changes
∴ q = increase in internal energy + energy used in doing work.
Above equation is mathematical form of I law of thermodynamics.
Question 59.
State the 2nd law of thermodynamics in any two ways.
Answer:
II law of thermodynamics :
Statements :
- “It is impossible for a self acting machine unaided by any external agency to convert heat from a body at low temperature to a body at higher temperature”.
- “All spontaneous processes are thermodynamically irreversible and entropy of the system increases in all spontaneous processes.”
- “For any spontaneous pirocess taking place in an isolated system, the change in entropy (∆S) is positive.”
Question 60.
Explain Gibbs energy.
Answer:
Gibbs energy (∆G) : The amount of energy available from a system which can be put to useful work at constant temperature and pressure is called Gibb’s energy. For explaining the criteria for spontaneity of a reaction, Gibb’s introduced thermodynamic function which involved both enthalpy (H) and entropy (S) functions. This is known as free energy function (G). This is given by the equation,
G = H – TS
Where ‘G’ is known as Gibbs energy (or) Gibbs function.
∆G = ∆H – T ∆S
∆Gsys = negative for spontaneous reactions (∆G < 0)
∆Gsys = positive for non – spontaneous reactions (∆G >0)
∆Gsys = zero equilibrium reactions (∆G = 0)
![]()
Question 61.
Explain the sponteneity of a reaction interms of Gibbs energy.
Answer:
To predict about the spontaneity of the reaction and
To redict the useful work that could be extract is the sign and magnitude of the quantities in Gibb’s equation is useful.
When a reaction is reversible it cannot proceed in both the direction with same case. In general the system would spontaneously change to configuration of lower free energy.
At equilibrium ∆G = 0
0 = ∆G° + RTLnK
∆rG° = -RTLnK = -2.303 RT log k
We know ∆rG° = ∆rH° – T∆rS° = -RT log k
For endothermic reaction ∆rH° may be large and positive
In such a case K is much less (K < 1)
In exothermic reactions ∆rH° is large and negative (K >1)
∴ For exothermic reaction
a) K must be large
b) ∆rG° is highly negative
c) ∆S° is highly positive
Hence with the sign and magnitude of the factors the yield of the product my be estimated.
∆Gsys = negative for spontaneous reactions (∆G < 0)
∆Gsys = positive for non – spontaneous reactions (∆G > 0)
∆Gsys = zero equilibrium reactions (∆G = 0)
Long Answer Questions
Question 1.
State and explain Hess’s Law of constant heat summation. Give example.
Answer:
Hess’s Law : Hess’s law states that the total amount of heat evolved or absorbed in a chemical reaction is always same whether the reaction is carried out in one step (or) in several steps. Illustration : This means that the heat of reaction depends only on the initial and final stages and not on the intermediate stages through which the reaction is carried out. Let us consider a reaction in which A gives D. The reaction is brought out in one step and let the heat of reaction be ∆H.
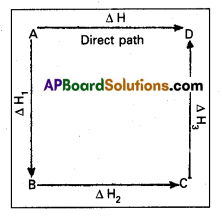
A → D; ∆H
Suppose the same reaction is brought out in three stages as follows –
A → B : ∆H1
B → C : ∆H2
C → D : ∆H3
The net heat of reaction is ∆H1 +∆H2+∆H3.
According to Hess law ∆H = ∆H1 + ∆H2 + ∆H3.
Ex : Consider the formation of CO2. It can be prepared in two ways.
1) Direct method : By heating carbon in excess of O2.
C(s) + O2(g) → CO2(g); ∆H = – 393.5 kJ
2) Indirect method : Carbon can be converted into C02 in the following two steps.
C(s) + \(\frac{1}{2}\)O2(g) → CO2(g); ∆H1 = – 110.5 kJ
CO (g) + \(\frac{1}{2}\) O2(g) → CO2(g); ∆H2 = – 283.02 kJ
Total ∆H = -393.52 kJ
The two ∆H values are same.
![]()
Question 2.
Explain the experiment to determine the internal energy change of a chemical reaction.
Answer:
Internal energy (U): “The total energy stored in the substance at constant temperature and pressure is called its internal energy (U)”.
It is state function and is an extensive property.
Internal energy change (∆U) is considered as the difference the internal energies of products and reactants.
∆U = (Up – Uf)
In any path taken (Q – W) is equal to ∆U.
Where Q = heat and W = work.
- The technique of measuring heats of reactions is called calorimetres. The apparatus used is calorimeter.
- Calorimeter is a vessel properly insulated and contains water as the calorimetric liquids
- A combustioble substance is burnt in oxygen.
- Heat evolved during the reaction is measured from the rise in 5 temperature.
- Here there is no worke done as ∆V = 0
- By the raise of temperature of water bath and calorimeter the amount of heat evolved can be determined.
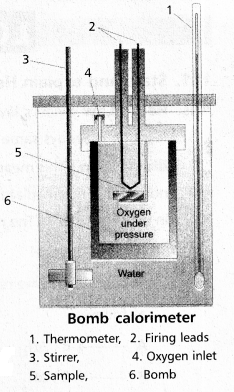
Internal Enegy All = Q. ∆t × \(\frac{\mathrm{M}}{\mathrm{m}}\)
Q = heat capacity
∆t = t2 – t1
M = molar mass of substance
m = mass of the substance
Question 3.
Explain the experiment to determine the enthalpy change of chemical reaction.
Answer:
Enthalpy (H) : “Enthalpy is the amount of heat exchanged by a system with its surroundings at constant pressure and temperature”.
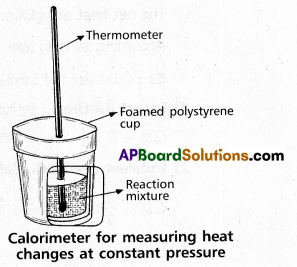
Mathematically, change in enthalpy ∆H = ∆E. P∆V
Enthalpy is state function. Thus, the magnitude of enthalpy change depends only upon the enthalpies in the initial and final states.
∆H = [Hproducts – Hreactants]
Heat change at constant pressure can be measured in a calorimeter at constant pressure ∆H = qp
∴ For Exothermic reaction ∆H = -ve
For Endothermic reaction ∆H = +ve
![]()
Question 4.
Explain the spontaneity of a reaction interms of enthalpy change, entropy change and Gibb’s energy change.
Answer:
Spontaneous reaction :
A process is said to be spontaneous if it occurs on its own without intervention of any external agency of any kind.
All natural processes are spontaneous.
Entropy increases in all spontaneous processes.
Change in entropy “(∆S) = positive” is a condition but is not necessary and sufficient condition for the spontaneous nature of a reaction.
Change in enthalpy “(∆H) = negative” may be a condition but not a necessary and sufficient condition for the spontaneous nature of a reaction.
At this juncture, “Gibbs” introduced another thermodynamic function which involves both enthalpy (H) and entropy (S) functions. This is known as free energy function (G). This is given by the equation, G = H – TS. ‘G’ is now referred as ‘Gibbs energy (or) Gibbs function.
“∆Gsys is negative” for spontaneous reactions (or) processes. Thus the spontaneity of a reaction and the algebraic signs of ∆H, ∆S, ∆G and the magnitude of ‘T’ can be related as follows :
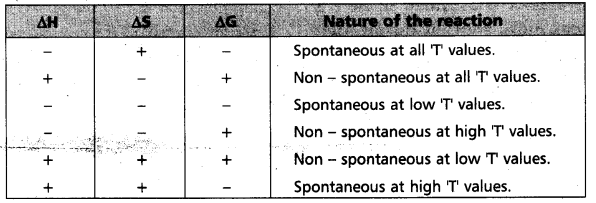
Change in entropy “(∆S) = positive” is a condition but is not necessary and sufficient condition for the spontaneous nature of a reaction.
For a spontaneous process change in entropy is- positive
∆S = +ve (spontaneous)
∆S = -ve (backward reaction is spontaneous)
∆S = 0 (Equilibrium reaction)
∴ ∆H = -ve, ∆S = +ve, ∆G = -ve then the reaction
Spontaneous at all T values (Reaction is irreversible)
Solved Problems
Question 1.
Express the change in internal energy of a system when
- No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have?
- No work is done on the system, but q amount of heat is taken out from the system and given to the surroundings. What type of wall does the system have?
- w amount of work is done by the system and q amount of heat is supplied to the system. What type of system would it be?
Solution:
- ∆U = wad wall is adiabatic
- ∆U = -q, thermally conducting walls
- ∆U = -q – w, closed system.
Question 2.
Two litres of an ideal gas at a pressure of 10 atm expand isothermally into a vacuum until its total volume is 10 litres. How much heat is absorbed and how much work is done in the expansion ?
Solution:
We have q = – w = pex (10 – 2) = 0(8) = 0
No work is done; no heat is absorbed.
Question 3.
Consider the same expansion, but this time against a constant external pressure of 1 atm.
Solution:
We have q = – w = pex (8) = (8) = 8 litre-atm
![]()
Question 4.
Consider the same expansion, to a final volume of 10 litres conducted reversibly.
Solution:
We have q = – w = 2.303 × 20 log \(\frac{10}{2}\)
= 32.2 litre-atm
Question 5.
If water vapour is assumed to be a perfect gas, molar enthalpy change for vapourisation of 1 mol of water at 1 bar and 100°C is 41 kJ mol-1. Calculate the internal energy change, when
i) 1 mol of water is vaporised at 1 bar pressure and 100°C.
ii) 1 mol of water is converted into ice.
Solution:
i) The change H2O (l) → H2O (g)
∆H = ∆U + ∆ngRT
or ∆U = ∆H – ∆ngRT, substituting the values, we get
∆U = 41.00 kJ mol-1 -1 × 8.3 J mol-1 K-1× 8.3 J mol-1 K-1 × 3731 |K|
= 41.00 kJ mol-1– 3.096 kJ mol-1
= 37.904 kJ mol-1
ii) The change H2O (l) → H2O (s)
There is negligible change in volume,
So, we can put p∆V = ∆ngRT ≈ 0 in this case,
∆H ≅ ∆U
so, ∆U = 41.00 kJ mol-1
Question 6.
1g of graphite is burnt in a bomb calorimeter in excess of oxygen at 298 K and 1 atmospheric pressure according to the equation
C (graphite) + O2 (g) → CO2 (g)
During the reaction, temperature rises from 298 K to 299 K. If the heat capacity of the bomb calorimeter is 20.7 kJ / K, what is the enthalpy change for the above reaction at 298 K and 1 atm ?
Solution:
Suppose q is the quantity of heat from the reaction mixture and Cv is the heat capacity of the calorimeter, then the quantity of heat absorbed by the calorimeter.
q = Cv × ∆T
Quantity of heat from the reaction will have the same magnitude but opposite sign because the heat lost by the system (reaction mixture) is equal to the heat gained by the calorimeter.
q = -Cv × ∆T = -20.7 kJ/K × (299 – 298)K
= -20.7 kJ
(Here, negative sign indicates the exothermic nature of the reaction)
Thus, ∆U for the combustion of the 1g of graphite = -20.7 kJ
For combustion of 1 mol of graphite,
= \(\frac{12.0 \mathrm{~g} \mathrm{~mol}^{-1} \times(-20.7 \mathrm{~kJ})}{1 \mathrm{~g}}\)
= -2.48 × 102 kJmol-1, Since ∆ng = 0,
∆ H = ∆ U = -2.48 × 102kJ mol-1
![]()
Question 7.
A swimmer coming out from a pool is covered with a film of water weighing about 18g. How much heat must be supplied to evaporate this water at 298 K ? Calculate the internal energy of vaporisation at 100°C.
∆vapH° for water at 373k = 40.66 kJ mol-1
Solution:
We can represent the process of evaporation as

Question 8.
The combustion of one mole of benzene takes place at 298 K and 1 atm. After combustion, CO2(g) and H2O (l) are produced and 3267.0 kJ of heat is liberated. Calculate the standard enthalpy of formation. ∆f H° of benzene. Standard enthalpies of formation of CO2(g) and H2O(l) are -393.5 kJ mol-1 and -285.83 kJ mol-1respectively.
Solution:
The formation reaction of benezene is given by:
6C (graphite) + 3H2 (g) → C6H6 (l);
∆fH° = ? ………………… (i)
The enthalpy of combustion of I mol of benzene is :
C6H6 (l) + \(\frac{15}{2}\) O2 (g) → 6CO2 (g) + 3H2O(l);
∆cH° =-3267 kJ mol-1 …………… (ii)
The enthalpy of formation of 1 mol of CO2 (g):
C(graphite) + O2 (g) → CO2 (g);
∆f H° = -393.5 kJ mol-1 ………………. (iii)
The enthalpy of formation of 1 mol of H2O(l) is:
H2 (g) + \(\frac{1}{2}\) O2 (g) → H2O(l) .
∆fH° = -285.83 kJ mol-1 ………………….. (iv)
Multiplying eqn. (iii) by 6 and eqn. (iv) by 3 we get:
6C (graphite) + 6O2 (g) → 6CO2 (g);
∆fH° = – 2361 kJ mol-1
3H2 (g) + \(\frac{3}{2}\) O2 (g) → 3H2O(l) .
∆fH° = – 857.49 kJ mol-1
Summing up the above two equations :
6C(graphite) + 3H2 (g) + \(\frac{15}{2}\) O2 (g) → 6CO2 (g) + 3H2O(l)
∆fH° = -3218.49 kJ mol-1 ………………. (v)
Reversing equation (ii);
6CO2 (g) + 3H2O(l) → C6H6 (l) + \(\frac{15}{2}\) O2
∆fH° = – 3267.0 kJ mol-1 ………………….. (vi)
adding equations (v) and (vi), we get
6C(graphite) + 3H2 (g) → C6H6 (l);
∆fH° = 48.51 kJ mol-1
![]()
Question 9.
Predict in which of the following, entropy increases/decreases :
i) A liquid crystallizes into a solid.
ii) Temperature of a crystalline solid is raised from 0 K to 115 K.
iii) 2NaHCO3 (s) → Na2 CO3 (s) + CO2 (g) + H2 O (g)
iv) H2 (g) → 2H(g)
Solution:
i) After freezing, the molecules attain an ordered state and therefore, entropy decreases.
ii) At 0 K, the contituent particles are static and entropy is minimum. If temperature is raised to 115 K, these begin to move and oscillate about their equilibrium positions in the lattice and system becomes more disordered, therefore entropy increases.
iii) Reactant, NaHCO3 is a solid and it has low entropy. Among products there are one solid and two gases. Therefore, the products represent a condition of higher entropy.
iv) Here one molecule gives two atoms i.e., number of particles increases leading to more disordered state. Two moles of H atoms have higher entropy than one mole of dihydrogen molecule.
Question 10.
For oxidation of iron,
4Fe(s) + 3O2 (g) → 2Fe2 O3 (s) entropy change is – 549.4 JK-1 mol-1 at 298 K. Inspite of negative entropy change of this reaction, why is the reaction spontaneous ?
(∆fH° for this reaction is -1648 × 103 J mol-1)
Solution:
One decides the spontaneity of a reaction by considering.
∆Stotal i.e., (∆Ssys + ∆Ssurr)- For calculating ∆Ssurr. we have to consider the heat absorbed by the surroundings which is equal to – ∆r ,H°. At temperature T, entropy change of the surroundings is ∆Ssurr = – \(\frac{\Delta_{\mathrm{r}} \mathrm{H}^{\circ}}{\mathrm{T}}\) (at constant pressure)
= –\(\frac{\left(-1648 \times 10^3 \mathrm{~J} \mathrm{~mol}^{-1}\right)}{298 \mathrm{~K}}\)
= 5530 JK-1 mol-1
Thus, total entropy change for this reaction.
∆rStotal = 5530 JK-1 mol-1 + (-549.4JK-1 mol-1)
= 4980.6 JK-1 mol-1
This shows that the above reaction is spontaneous.
Question 11.
Calculate ∆rG° for conversion of oxygen to ozone, 3/2 O2(g) → O3(g) at 298 K. if Kp for this conversion is 2.47 × 10-29.
Solution:
We know ∆rG° = – 2.303 RT log Kp and
R = 8.314 JK-1 mol-1
Therefore, ∆rG° = – 2.303 (8.314 J K-1 mol-1) × (298 K) (log 2.47 × 10-29)
= 163000 J mol-1
= 163 kJ mol-1
![]()
Question 12.
Find out the value of equilibrium constant for the following reaction at 298 K.
2NH3 (g) + CO2 (g) ⇌ NH2 CONH2 (aq) + H2O(l)
Standard Gibbs energy change, ∆rG° at the given temperature is – 13.6 kJ mol-1.
Solution:

Question 13.
At 60°C, dinitrogen tetroxide is fifty percent dissociated. Calculate the standard free energy change at this temperature and at one atmosphere.
Solution:
N2O4(g) ⇌ 2NO2(g)
If N2O4 is 50% dissociated, the mole fraction of both the substances is given by
xN2O4 = \(\frac{1-0.5}{1+0.5}\) ; xNO2 = \(\frac{2 \times 0.5}{1+0.5}\)
PN2O4 = \(\frac{0.5}{1.5}\) × 1 atm, PNO2 = \(\frac{1}{1.5}\) × 1 atm.
The equilibrium constant Kp is given by
Kp = \(\frac{\left(\mathrm{p}_{\mathrm{NO}_2}\right)^2}{\mathrm{p}_{\mathrm{N}_2 \mathrm{O}_4}}=\frac{1.5}{(1.5)^2(0.5)}\)
= 1.33 atm.
Since
∆rG° = – RT l n Kp
∆rG° = (-8.314 JK-1 mol-1) × (333 K) × (2.303) × (0.1239)
= – 763.8 kJ mol-1