AP Inter 1st Year Maths 1A Important Questions Chapter 1 ప్రమేయాలు

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 1 ప్రమేయాలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 1 ప్రమేయాలు

సాధించిన సమస్యలు

ప్రశ్న 1
f: R- {0} → R ను f(x) = x + \(\frac{1}{x}\) గా నిర్వచిస్తే (f(x))² = f(x²) + f(1) అని చూపండి.
సాధన:
f : R – {0} → R,
f(x) = x + \(\frac{1}{x}\)
ఇప్పుడు f(x²) + f(1) = (x² + \(\frac{1}{x^2}\)) + (1 + \(\frac{1}{1}\))
= x² + 2 + \(\frac{1}{x^2}\)
= \(\left(x+\frac{1}{x}\right)^2\) = (f(x))²
∴(f(x))² = f(x²) + f(1)

ప్రశ్న 2.
f ప్రమేయాన్ని [Mar. ’14]

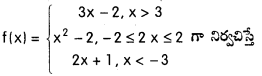
f(4), f(2.5), f(-2), f(-4), f(0), f(-7) కనుక్కోండి.
సాధన:
f ప్రదేశం (−∞, – 3) ∪ (-2, 2] ∪ (3, ∞)
i) f(x)=3x – 2, x > 3
f(4) = 3(4) – 2 = 10

ii) 2.5, f ప్రదేశంలో లేదు. కనుక f(2.5) నిర్వచితం కాదు.

iii) ∵ f(x) = x² – 2, -2 ≤ x ≤ 2 కాబట్టి
f(-2) = (-2)² – 2 = 4 – 2 = 2

iv) ∵ f(x) = 2x + 1, x < -3 కాబట్టి
f(-4) = 2(-4) + 1 – 8 + 1 = -7

v) ∵ f(x) = x² – 2, -2 ≤ x ≤ 25
f(0) = (0)² – 2 = 0 – 2 = -2

vi) ∵ f(x) = 2x + 1, x < -3 కాబట్టి
f(-7) = 2(-7) +1 = -14 + 1 = -13

ప్రశ్న 3.
A = {0, \(\frac{\pi}{6}\), \(\frac{\pi}{4}\), \(\frac{\pi}{3}\), \(\frac{\pi}{2}\)}, f : A → B సంగ్రస్తం అయి, f(x) = cos X గా నిర్వచిస్తే, B కనుక్కోండి. [May ’11; Mar. ’11]
సాధన:
f : A → B సంగ్రస్తం
f(x) = cos x
B = f వ్యాప్తి = f(A)
= \(\left\{f(0), f\left(\frac{\pi}{6}\right), f\left(\frac{\pi}{4}\right), f\left(\frac{\pi}{3}\right), f\left(\frac{\pi}{2}\right)\right\}\)
= \(\left\{1, \frac{\sqrt{3}}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}, 0\right\}\)
= \(\left\{-1, \frac{\sqrt{3}}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}, 0\right\}\)

ప్రశ్న 4.
f : R → R ను f(x) = \(\frac{e^{|x|}-e^{-x}}{e^x+e^{-x}}\) గా నిర్వచిస్తే, f అన్వేకం, సంగ్రస్తం, ద్విగుణం అవుతాయేమో నిర్ణయించండి.
సాధన:
f : R→ R ను

y = 1 కి f(x) = 1 అయ్యేటట్లు R లో x ఉండదు.
⇒ కాబట్టి f సంగ్రస్తం కాదు.
ఒకవేళ x ∈R కు f(x) = 1 అయితే
\(\frac{e^{|x|}-e^{-x}}{e^x+e^{-x}}\) = 1
⇒ e^|x| – e^x = e^x + e^-x, కాబట్టి x ≠ 0 స్పష్టం.
x > 0, అయితే
e^x – e^-x = e^x + e^-x ⇒ e^-x = e^-x అసాధ్యం.
x < 0, అయితే
e^-x – e^-x = e^x + e^-x
⇒ -e^-x = e^x అసాధ్యం.

ప్రశ్న 5.
f : R → R ను
నిర్వచిస్తే, f అన్వేకం, సంగ్రస్తం, ద్విగుణం అవుతాయేమో పరిశీలించండి.
సాధన:
3 > 2 కాబట్టి f(3) = 3
1 < 2 కాబట్టి f(1) = 5(1) – 2 ∴ 1, 3 లకు ఒకే f- ప్రతిబింబం ఉంది. కాబట్టి f అన్వేకం కాదు. సహప్రదేశం లోని y కి, y > 2 లేదా y ≤ 2 కావాలి.
y > 2 అయితే x = y ∈ R, f(x) = x = y
y ≤ 2 అయితే x = \(\frac{y+2}{5}\)∈ R
x = \(\frac{y+2}{5}\) < 1
∴ f(x) = 5x – 2 = 5\(\left[\frac{y+2}{5}\right]\) – 2 = y
∴f ఎ. సంగ్రస్తం
f అన్వేకం కాదు కాబట్టి f ద్విగుణ ప్రమేయం కాదు.

ప్రశ్న 6.
2^x + 2^y = 2 సమీకరణం ద్వారా నిర్వచింపబడ్డ ప్రమేయం y(x) ప్రదేశం కనుక్కోండి.
సాధన:
2^x = 2 – 2^y < 2 (∵ 2^y > 0)
⇒ log₂2^x < log₂2
⇒ x < 1
∴ ప్రదేశం = (-∞, 1).

ప్రశ్న 7.
f : R → R f (x + y) = f(x) + f(y) ∀ x, y ∈ R, f(1) = 7, గా నిర్వచిస్తే \(\sum_{r=1}^n f(r)\) కనుక్కోండి.
సాధన:
f(2) = f (1 + 1) = f (1) + f (1) = 2f (1).
f(3) = f(2+1) = f (2) + f (1) = 3f (1).
ఇలాగే f(r) = rf (1).
∴ \(\sum_{r=1}^n f(r)\) = f (1) + f(2) + ………. + f(n)
= f (1) + 2f (1) + …… +n f (1)
= f(1) (1 + 2+ …………….. +n)
= \(\frac{7 n(n+1)}{2}\)

ప్రశ్న 8.
f(x) = \(\frac{\cos ^2 x+\sin ^4 x}{\sin ^2 x+\cos ^4 x}\) ∀ x ∈ R అయితే f (2012) = 1 అని చూపండి.
సాధన:

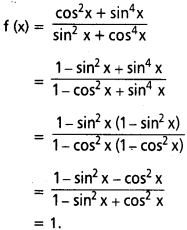
∴ f (2012) = 1.

ప్రశ్న 9.
f : R → R, g : R → R f(x) = 4x – 1, g(x) = x² + 2 గా నిర్వచిస్తే
i) (gof) (x)
ii) (gof) \(\left(\frac{a+1}{4}\right)\)
iii) (fof) (x)
iv) go(fof) (0) కనుక్కోండి. [Mar. ’05]
సాధన:
f : R → R, g : R → R
f(x) =4x – 1, g(x) = x² + 2
i) (gof) (x) = g(f(x))
= g(4x – 1). ∵ f(x) = 4x – 1
= (4x – 1)² + 2 ∵ g(x) = x² + 2
= 16x² – 8x + 1 + 2
= 16x² – 8x + 3

ii) (gof) \(\left(\frac{a+1}{4}\right)\) = \(g\left(f\left(\frac{a+1}{4}\right)\right)\)
= \(g\left(4\left(\frac{a+1}{4}\right)-1\right)\)
= g(a)
= a² + 2

iii) (fof) (x) = f(f(x))
= f(4x – 1) ∵ f(x) = 4x – 1
= 4(4x – 1) – 1
= 16x – 4 – 1
= 16x – 5

iv) (fof) (0) = f(f(0))
= f(4 × 0 – 1)
= f(-1)
= 4(-1) – 1 = -5
ఇప్పుడు (fof) (0) = g(-5) = (-5)² + 2 = 27

ప్రశ్న 10.
f : [0, 3] → [0,3],
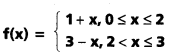గానిర్వచిస్తే
f[0, 3] ⊆ [0, 3] అని చూపి fof కనుక్కోండి.
సాధన:
0 ≤ x ≤ 2 ⇒ 1 ≤ 1 + x ≤ 3 …………….. (1)
2 < x <3 ⇒ -3 ≤ x ≤ -2
⇒ 3 – 3 ≤ 3 – x ≤ 3 – 2
⇒ 0 ≤ 3 – x < 1 ……………… (2)
(1), (2) ల నుండి
f[0, 3] ⊆ [0, 3]
0 ≤ x ≤ 1, అయితే
(fof) (x) = f(f(x))
f(1 + x)=1+ (1 + x) = 2 + x [∵ 1 ≤ 1 + x ≤ 2]
1 < x ≤ 2, అయితే
(fof) (x) = = f(f(x))
= f(1 + x)
= 3 – (1 + x)
= 2x, [∵ 2 < 1 + x ≤ 3]
2 < x ≤ 3, అయితే
(fof) (x) = f(f(x))
= f(3 – x)
= 1 + (3 – x)
= 4 – x, [∵ 0 ≤ 3 – x < 1]

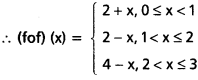
ప్రశ్న 11.
f, g : R→ R ప్రమేయాలను , అని నిర్వచిస్తే
(fog) (π) + (gof) (e).
సాధన:
(fog) (π) = f (g (π)) = f (0) = 0
(gof) (e) = (f (e)) = g (1) = -1.
∴ (fog) (π) + (gof) (e) = -1.

ప్రశ్న 12.
A = {1, 2, 3}, B = {a, b, c}, C = (p, q, r} అనుకొందాం f : A → B, g : B → C లను f = {(1, a), (2, c), (3, b)}, g = {(a, q), (b, r), (c, p)} π గా నిర్వచిస్తే f^-1og^-1= (g o f)^-1 అని చూపండి.
సాధన:
f = {(1, a), (2, c), (3, b)}
g = {(a, q), (b, r), (c, p)}లు కనుక
అప్పుడు go f = {(1, q), (2, p), (3, r)}
⇒ (gof)^-1 = {(q, 1), (p, 2), (r, 3)}
g^-1 = {(q, a), (r, b), (p, c)},
f^-1 = {(a, 1), (c, 2), (b, 3)} కనుక
f^-1og^-1 = {(q, 1), (r, 3), (p, 2)}
∴ (gof)^-1 = f^-1 o g^-1

ప్రశ్న 13.
f : Q→ Q, f(x) = 5x + 4 m గా ప్రతీ x ∈ Q నిర్వచిస్తే, f ద్విగుణ ప్రమేయం అని చూపి కనుక్కోండి. [May ’05]
సాధన:
x₁, x₂, ∈ Q,
f(x₁) = f(x₂)
⇒ 5x₁ + 4 = 5x₂ + 4
⇒ 5x₁ = 5x₂
⇒ x₁ = x₂
∴ f అన్వేకం
y ∈ Q అయితే x = \(\frac{y-4}{5}\) ∈ Q వ్యవస్థితం
f(x) = \(f\left(\frac{y-4}{5}\right)=5\left(\frac{y-4}{5}\right)\) + 4 = y
∴ f సంగ్రస్తం
కనుక ద్విగుణ ప్రమేయం
∴ f^-1 : Q → Q వ్యవస్థితం. కాని Q లో ప్రతీ x కు
(fof^-1) (x) = I(x)
⇒ f(f^-1(x)) = x, ‘.’ f(x) = 5x + 4
⇒ 5 f^-1(x) + 4 = x
⇒ f^-1(x) = \(\frac{x-4}{5}\) ∀ x ∈ Q

ప్రశ్న 14.
ఈ కింది వాస్తవ మూల్య ప్రమేయాలకు ప్రదేశాలు తీసుకోండి.
i) f(x) = \(\frac{1}{6 x-x^2-5}\)
సాధన:
f(x) = \(\frac{1}{6 x-x^2-5}=\frac{1}{(x-1)(5-x)}\) ∈ R
⇔ (x – 1) (5 – x) ≠ 0
⇔ x ≠ 1, 5
∴f ప్రదేశం R – {1, 5}.

ii) f(x) = \(\frac{1}{\sqrt{x^2-a^2}}\) (a > 0) [(A.P) Mar ’15]
సాధన:
f(x) = \(\frac{1}{\sqrt{x^2-a^2}}\) ∈ R
⇔ x² – a² > 0·
⇔ (x + a) (x – a) > 0
⇔ x ∈ (-∞, -a) ∪ (a,∞)
∴f ప్రదేశం
(-∞, -a) ∪ (a, ∞) = R-[-a, a]

iii) f(x) = \(\sqrt{(x+2)(x-3)}\)
సాధన:
f(x) = \(\sqrt{(x+2)(x-3)}\) ∈ R
⇔ (x + 2) (x – 3) > 0
⇔ x ∈ (-∞, -2) ∪ [3, ∞)
∴f ప్రదేశం
(-∞, -2] ∪ [3, ∞) = R(-2, 3)

iv) f(x) = \(\sqrt{(x-\alpha)(\beta-x)}\) (0 < α < β) సాధన: f(x) = \(\sqrt{(x-\alpha)(\beta-x)}\) ∈ R ⇔ (x – α) (β – x) > 0
⇔ α ≤ x ≤ β; (α <β)
⇔x ∈ [α, β]
∴ f ప్రదేశం [α, β]

v) f(x) = \(\sqrt{2-x}\) + \(\sqrt{1+x}\)
సాధన:
f(x) = \(\sqrt{2-x}\) + \(\sqrt{1+x}\) ∈ R
⇔ 2 – x ≥ 0, 1 + x ≥ 0
⇔ 2 ≥ x, x ≥ -1
⇔ -1 ≤ x ≤ 2
⇔ x ∈ [-1, ]
∴ f ప్రదేశం [-1, 2].

vi) f(x) = \(\sqrt{x^2-1}+\frac{1}{\sqrt{x^2-3 x+2}}\)
సాధన:
f(x) = \(\sqrt{x^2-1}+\frac{1}{\sqrt{x^2-3 x+2}}\) ∈ R
⇔ x² – 1 ≥ 0, x² – 3x + 2 > 0
⇔ (x + 1) (x = 1) ≥ 0, (x – 1) (x – 2) > 0
⇔ x ∈ (∞, -1] ∪ [1, ∞), x ∈ (-∞, 1) ∪(2, ∞)
⇔ x ∈ (R – (-1, 1)) ∩ (R-[1, 2])
⇔ x ∈ R – {(1, 1) ∪ [1, 2]}
⇔ x ∈ R – (-1, 2]
⇔ x ∈ (-∞, -1] ∪ (2, ∞)
∴ f ప్రదేశం
(-∞, -1] ∪(2, ∞) = R – (-1, 2]

vii) f(x) = \(\frac{1}{\sqrt{|x|-x}}\) ∈ R
సాధన:
f(x) = \(\frac{1}{\sqrt{|x|-x}}\) ∈ R
⇔ |x| – x > 0
⇔ |x| > x
⇔ x ∈ (-∞, 0)
∴ f ప్రదేశం (-∞, 0)

viii) f(x) = \(\sqrt{|\mathrm{x}|-\mathrm{x}}\)
సాధన:
f(x) = \(\sqrt{|\mathrm{x}|-\mathrm{x}}\) ∈ R
⇔ |x| – x ≥ 0
⇔ |x| ≥ x
⇔ x ∈ R
∴ f ప్రదేశం R.

ప్రశ్న 15.
f = {(4, 5), (5, 6), (6, -4)}, g = {(4, 4), (6, 5), (8, 5)} అయితే
i) f + g
ii) f – g
iii) 2f + 4g
iv) f + 4
v) fg
vi) \(\frac{\mathrm{f}}{\mathrm{g}}\)
vii) |f|
viii) \(\sqrt{\mathrm{f}}\)
ix) f²
(x) f³ లు కనుక్కోండి.
సాధన:
f = {(4, 5), (5, 6), (6, -4)}
g= {(4, 4), (6, 5), (8, 5)}
f ప్రదేశం = {4, 5, 6} = A
g ప్రదేశం = {4, 6, 8) = B
f ± g ప్రదేశం = A ∩ B = {4, 6}
i) f + g = {4, 5 + (-4), (6, – 4 + 5)}
= {(4, 1), (6, 1)}

ii) f – g = {(4, 5 – (-4)), (6, -4, -5)}
= {(4, 9), (6, -9)}

iii) 2f ప్రదేశం = A = {4, 5, 6}
4g ప్రదేశం = B = {4, 6, 8}
2f + 4g ప్రదేశం = A ∩ B = (4, 6)
∴ 2f = {(4, 10), (5, 12), (6, -8)}
4g = {(4, -16), (6, 20), (8, 20)}
∴ 2f + 4g = {(4, 10 + (-16), 6, -8 + 20)}
= {(4, −6), (6, 12)}

iv) f + 4 ప్రదేశం = A = {4, 5, 6}
f + 4 = {4, 5 + 4), (5, 6 + 4), (6, – 4 + 4)}
= {(4, 9), (5, 10), (6, 0)}

v) fg ప్రదేశం = A ∩ B = {4, 6}
fg = {(4, (5) (-4), (6, (-4) (5))}
= {(4, -20), (6, – 20)}

vi) \(\frac{\mathrm{f}}{\mathrm{g}}\) ప్రదేశం = {4, 6}
∴\(\frac{f}{g}=\left\{\left(4, \frac{-5}{4}\right),\left(6, \frac{-4}{5}\right)\right\}\)

vii) |f| ప్రదేశం = {4, 5, 6}
∴ |f| = {(4, |5|), (5, |6|), (6, |-4|)}
= {(4, 5), (5, 6), (6, 4)}

viii) \(\sqrt{\mathrm{f}}\) ప్రదేశం = {4, 5}
∴ \(\sqrt{\mathrm{f}}\) = {(4, \(\sqrt{5}\)), (5, \(\sqrt{6}\))}

ix) f² ప్రదేశం = {4, 5, 6} = A
∴ f² = {(4, (5)²), (5, (6)², (6, (-4)²)}
f² = {(4, 25), (5, 36), (6, 16)}

x) f³ ప్రదేశం = A = {4, 5, 6}
∴ f³ = {(4, (5³), (5, 6³), (6, (-4)³}
= {(4, 125), (5, 216), (6, -64)}

ప్రశ్న 16.
కింది వాస్తవ మూల్య ప్రమేయాల ప్రదేశాలు, వ్యాప్తులు కనుక్కోండి.
i) f(x) = \(\frac{2+x}{2-x}\)
ii) f(x) = \(\frac{x}{1+x^2}\)
iii) f(x) = \(\sqrt{9-x^2}\)
సాధన:
i) f(x) = \(\frac{2+x}{2-x}\) ∈ R
⇔ 2 – x ≠ 0 ⇔ x ≠ 2 ⇔ x ∈ R – {2}
∴ f ప్రదేశం R – {2}
f(x) = \(\frac{y}{1}=\frac{2+x}{2-x}\) అనుకోండి.
⇒ \(\frac{y+1}{y-1}=\frac{(2+x)+(2-x)}{(2+x)-(2-x)}\)
⇒ \(\frac{y+1}{y-1}=\frac{4}{2 x}\)
⇒ x = \(\frac{2(y-1)}{y+1}\)
y + 1 = 0
(i.e.,) y = -1 కి x నిర్వచితం కాదు
∴ f వ్యాప్తి = R – {1}.

ii) f(x) = \(\frac{x}{1+x^2}\)
సాధన:
f(x) = \(\frac{x}{1+x^2}\) ∈ R
∴ ∀ x ∈ R, x² + 1 ≠ 0
f ప్రదేశం R
f(x) = y = \(\frac{x}{1+x^2}\) అనుకుందాం.
⇒ x²y – x + y = 0
⇒ x = \(\frac{-(-1) \pm \sqrt{1-4 y^2}}{y}\), వాస్తవ సంఖ్య
⇔ 1 – 4y² ≥ 0, y ≠ 0
⇔ (1 – 2y) (1 + 2y) ≥ 0, y ⇔ 0
⇔ y ∈ \(\left[-\frac{1}{2}, \frac{1}{2}\right]\) – {0}
కాని x = 0 ⇒ y = 0
∴ f వ్యాప్తి = \(\left[-\frac{1}{2}, \frac{1}{2}\right]\)

iii) f(x) = \(\sqrt{9-x^2}\) [(T.S) Mar ’15]
సాధన:
f(x) = \(\sqrt{9-x^2}\) ∈ R
⇔ 9 – x² ≥ 0
⇔ (3 + x) (3 – x) ≥ 0
⇔ x ∈ [-3, 3]
∴ f ప్రదేశం [-3, 3]
f(x) = y = \(\sqrt{9-x^2}\) అనుకుందాం
⇒ x = \(\sqrt{9-y^2}\) ∈ R.
⇔ 9 – y² ⇔ (3 + y) (3 – y) ≥ 0
∴ -3 ≤ y ≤ 3
కానీ f(x) రుణేతర వాస్తవ సంఖ్యలు మాత్రమే తీసుకుందాం.
∴ f వ్యాప్తి = [0, 3].

ప్రశ్న 17.
f(x) = x², g(x) = |x| గా నిర్వచిస్తే, క్రింది ప్రమేయాలను కనుక్కోండి.
i) f + g,
ii) f – g,
iii) fg,
iv) 2f,
v) f²,
vi) f + 3
సాధన:
f(x) = x²

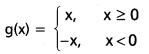
f ప్రదేశం = g ప్రదేశం = R
కాబట్టి (i) నుంచి (vi) వరకు ప్రమేయాల ప్రదేశం R

i) (f + g) (x) = f(x) + g(x)

iv) 2f (x) = 2 f(x) = 2x²
v) f(x) = (f(x))² = (x²)² = x⁴
vi) f + 3 (x) = f(x) + 3 = x² + 3.

ప్రశ్న 18.
ఈ కింది ప్రమేయాలలో ఏవి సరి లేదా బేసి ప్రమేయాలో నిర్ధారించండి.
i) f(x) = a^x – a^-x + sin x
సాధన:
f(x) = a^x – a^-x + sin x
∴ f(x) = a^x – a^-x + sin (-x)
= a^-x – a^x – sin x
= – (a^x – a^-x + sin x) = – f(x)
∴ f(x) బేసి ప్రమేయం.

ii) f(x) = x\(\left(\frac{e^x-1}{e^x+1}\right)\)
సాధన:

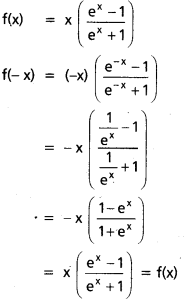
∴ f సరి ప్రమేయం.

iii) f(x) = log(x + \(\sqrt{x^2+1}\))
సాధన:

∴ f బేసి ప్రమేయం.

ప్రశ్న 19.
కింది వాస్తవ మూల్య ప్రమేయాల ప్రదేశాలు కనుక్కోండి.
i) f(x) = \(\frac{1}{\sqrt{[x]^2-[x]-2}}\)
సాధన:
f(x) = \(\frac{1}{\sqrt{[x]^2-[x]-2}}\) ∈ R
⇔ [x]² – [x] – 2 > 0
⇔ ([x] + 1) ([x] – 2] > 0
⇔ [x] < – 1, (or) [x] > 2
కాని [x] < -1 [x] ⇒ -2, -3, -4, ……….
⇒ x < -1 [x] > 2 ⇒ [x] = 3, 4, 5, …….. ⇒ x ≥ 3
∴ f ప్రదేశం = (-∞, -1) ∪ [3, ∞]
= R- [-1, 3)

ii) f(x) = log (x – [x])
సాధన:
f(x) = log (x – [x]) ∈ R
⇔ x – [x] > 0
⇔ x > [x]
⇔ x పూర్ణ సంఖ్య కాదు.
∴ f ప్రదేశం R – Z

iii) f(x) = \(\sqrt{\log _{10}\left(\frac{3-x}{x}\right)}\)
సాధన:

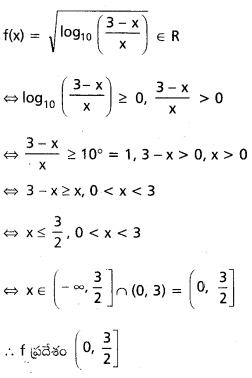
iv) f(x) = \(\sqrt{x+2}+\frac{1}{\log _{10}(1-x)}\)
సాధన:
f(x) = \(\sqrt{x+2}+\frac{1}{\log _{10}(1-x)}\) R
⇔ x + 2 ≥ 0, 1 – x > 0, 1 – x ≠ 1
⇔x ≥ – 2, 1 > x, x ≠ 0
⇔ x ∈ [-2, ∞) ∩ (-∞, 1) – {0}
⇔x ∈ [-2, 1) – {0}
∴ f ప్రదేశం [- 2, 1) – {0}

v) f(x) = \(\frac{\sqrt{3+x}+\sqrt{3-x}}{x}\)
సాధన:
f(x) = \(\frac{\sqrt{3+x}+\sqrt{3-x}}{x}\) ∈ R
⇔ 3 + x ≥ 0, 3 – x ≥ 0, x ≠ 0
⇔ x – 3, x ≤ 3, x ≠ 0
⇔ -3 ≤ x ≤ 3, x ≠ 0
⇔ x ∈ [- 3,3 ] x ≠ 0
⇔ x ∈ [- 3, 3] – {0}
∴ f ప్రదేశం [- 3, 3] – {0}

ప్రశ్న 20.
f : A → B, g : B → C లు అన్వేక ప్రమేయాలు అనుకుందాం. అప్పుడు gof : A → C కూడా అన్వేకం అవుతుంది అని నిరూపింపుము.
సాధన:
f : A → B, g : B → C లు అన్వేకాలు
∴ gof : A → C
gof అన్వేకం అని చూపటానికి
a₁, a₂ ∈A అనుకొనుము.
∴ f(a₁), f(a₂) ∈ B మరియు g (f(a₁)),
g(f(a₂)) ∈ C అనగా (gof) (a₁), gof (a₂) ∈ C
ఇప్పుడు (gof) (a₁) = gof (a₂).
⇒ g(f(a₁)) = g(f(a₂))
⇒ f(a₁) = f(a₂) (∵ g అన్వేకం)
⇒ a₁ = a₁ (∵ f అన్వేకము)
అందువలన gof : A → C అన్వేక ప్రమేయము. అయితే f : A → B, g : B → C మరియు gof అన్వేకము.
అప్పుడు f మరియు g అన్వేకము కావలసిన అవసరం లేదు.
A = {1, 2}, B = {p, q, r), C = {s, t} అనుకొనుము.
f = {(1, p), (2, q)} మరియు
g = {(p, s), (q, t), (r, t)}
ఇప్పుడు gof = {(1, s), (2, t)}
gof : A → C అన్వేకం
కాని g : B → C అన్వేకము కాదు.

ప్రశ్న 21.
f : A → B, g : B → C లు సంగ్రస్త ప్రమేయాలు అనుకుందాం. అప్పుడు gof A → C సంగ్రస్త ప్రమేయం అగును అని నిరూపించుము. [May ’08]
సాధన:
c ∈ C అనుకుందాం. g : B → C సంగ్రస్త ప్రమేయం
కాబట్టి g(b) = c అయ్యేటట్లు b ∈ B వ్యవస్థితం.
f : A → B సంగ్రస్తం కనుక, f(a) = b అయ్యేటట్లు a ∈ A ఉంటుంది.
∴ c = g(b) = g(f(a)) = (gof) (a)
∴ C ∈ C = (gof) (a) (gof) (a) = c అయ్యేలా a ∈ A వ్యవస్థితం.
కనుక gof : A → C సంగ్రస్తం.

ప్రశ్న 22.
f : A → B, g: B → C, gof సంగ్రస్త అనుకుందాం. అప్పుడు g సంగ్రస్తం అగును అని నిరూపించుము.
సాధన:
c ∈ C అనుకుందాం. gof : A → C సంగ్రస్త ప్రమేయం కనుక (gof) (a) = C అయ్యేటట్లు a ∈ A ఉంటుంది..
అంటే g(f(a)) = c, b = c, b = f(a) అనుకుందాం.
అప్పుడు b ∈ B, g(b) = c
∴ g సంగ్రస్తం

ప్రశ్న 23.
f : A → B, g : B→ C, h : C → D అనుకుందాం. ho(gof) = (hog) అని నిరూపించుము.
సాధన:
f : A → B మరియు g : B → C ⇒ gof : A → C
ఇప్పుడు gof : A → C మరియు h : C → D
⇒ ho(gof) : A → D
అదే విధంగా (hog)of : A → D
అందువలన ho(gof) మరియు (hog) of ప్రమేయాలు ఒకే ప్రదేశాన్ని, ఒకే సహప్రదేశాన్ని కలిగి ఉన్నాయి.
a ∈ A. అనుకుందాం
[ho(gof)] (a) = h[(gof)(a)] = h[g(f(a))]
= (ho g) [f(a)] = [(hog)of] (a)
∴ ho(gof) = (hog)of.
సూచన : ప్రమేయాల సంయుక్తత సాహచర్య న్యాయాన్ని పాటిస్తుంది.

ప్రశ్న 24.
f : A → B, I_A, I_B లు తత్సమ ప్రమేయాలు అయిన fo I_A = f = I_B అని చూపండి. [Mar. ’08]
సాధన:
f : A → B అనుకుందాం. I_A, I_B లు A, B లలో తత్సమ ప్రమేయాలైతే foI_A = I_Bof = f
I_A : A → A, f : A → B కనుక A నుంచి B కి foI_A ప్రమేయం.
f : A → B, I_B : B → B కనుక A నుంచి B కి I_Bof ప్రమేయం.
foI_A, f, I_Bof ప్రమేయాలకు ప్రదేశం A
అప్పుడు (foI_A) (a) = f (I_A(a)) = f(a)[∵ I_A(a) = a] ∀a ∈ A కి
∴ foI_A = f …………….. (1)
(I_Bof) (a) = I_B(f (a)) = f(a) ∀a ∈ A
∴ I_Bof = f ………….. (2)
(1), (2) లు నుంచి foI_A = f = I_Bof

ప్రశ్న 25.
A, B లు శూన్యేతర సమితులు. f : A → B ద్విగుణమైతే, f^-1 : B → A ద్విగుణం అని నిరూపించుము.
సాధన:
f : A → B అన్వేకం అనుశీరిందాం.
స్పష్టంగా f(A) నుంచి A కి f^-1 ఒక సంబంధం.
b ∈ f(A) అనుశీరిందాం. f అన్వేకం కనుక f(a) = b అయ్యేటట్లు A లో ఒకే ఒక మూలకం a ఉంటుంది.
అందువల్ల ఇచ్చిన b ∈ f(A) కు (a, b) ∈ f అయ్యేటట్లు A లో ఒకే ఒక మూలకం a ఉంటుంది. అందువల్ల ఇచ్చిన b ∈ f(A) కు (b, a) ∈ f^-1 అయ్యేటట్లు ఒకే ఒక a ∈ A ఉంటుంది. అందువల్ల f(A) నుంచి A కు f^-1 ఒక ప్రమేయం. ఇంకా f^-1(b) = a ⇒ f(a) = a ⇒ f(a) = b స్పష్టంగా f^-1 సంగ్రస్త
ప్రమేయం.
b₁, b₂ ∈ f(A) అయి f^-1(b₁) = f^-1(b₂) = a
అనుకుందాం. అప్పుడు b₁ = f(a) = b₂
అందువల్ల f^-1 అన్వేకం. అందువల్ల f^-1 : B → A ద్విగుణం.

ప్రశ్న 26.
f : A → B ద్విగుణ ప్రమేయం అనుకుందాం. అప్పుడు fof^-1 = I_B, f^-1of = I_A అని నిరూపించుము. [(A.P) Mar. ’15, ’07; May ’07, ’06]
సాధన :
A నుండి Bకి f ద్విగుణ ప్రమేయం కనుక B నుంచి A కి f^-1 ద్విగుణ ప్రమేయం. అందువల్ల B నుంచి B కి fof^-1 ద్విగుణం. ఇలాగే A నుంచి A కి f^-1of ద్విగుణం. B నుంచి B కి I_B ద్విగుణ ప్రమేయం. A నుంచి A కి I_A ద్విగుణం అని తెలుసు. fof^-1, I_B ప్రమేయాల ప్రదేశం ఒక్కటే. అది B . b ∈ B అనుకుందాం. f^-1(b) = a అనుకుందాం. అప్పుడు a ∈ A, f(a) = b.
ఇంకా (fof^-1) (b) = f(f^-1(b))
= f(a) = b = I_B(b)
అంటే (fof^-1) (b) = I_B(b)
కనుక fof^-1 = I_B
f^-1of, I_A ప్రమేయాలకు ప్రదేశం A.
x ∈ A అనుకుందాం.
f(x) = y అనుకుందాం.
అప్పుడు ye B, f^-1(y) = x
ఇంకా (f^-1of) (x) = f^-1(f(x))
= f^-1(y) = x = I_A(x)
అంటే (f^-1of) (x) = I_A(x)
అందువల్ల f^-1of = I_A.

ప్రశ్న 27.
f : A → B, g : B → A, gof = I_A, fog = I_B అనుకుందాం. అప్పుడు f ద్విగుణ ప్రమేయం మరియు g = f^-1 అని నిరూపించుము.
సాధన:
i) f అన్వేక ప్రమేయమని చూపిద్దాం.
a₁, a₂ ∈ A అనుకుందాం.
f(a₁) = f(a₂) ⇒ g[f(a₁)] = g[f(a₂)]
⇒ (gof) (a₁) = (gof) (a₂)
⇒ a₁ = a₂ [∵ gof అన్వేకం]
f అన్వేక ప్రమేయం.

ii) f సంగ్రస్త ప్రమేయమని చూపిద్దాం.
b ∈B అనుకొందాం..
∴ b = I_B (b) = fog (b)
⇒ b = f{g(b)}} =→ f{g(b)} = b
f ప్రమేయం ద్వారా b కొరకు g(b) ∈ A అయ్యే విధంగా ఒక పూర్వ ప్రతిబింబము వ్యవస్థితము.
∴ f అన్వేకము మరియు సంగ్రస్తము
∴ f ద్విగుణ ప్రమేయం

iii) ఇప్పుడు g = f^-1 అని చూపిద్దాం.
g, f^-1 ప్రమేయాలు ఒకే ప్రదేశం B ని కలిసి ఉన్నాయి.
b ∈ B, g(b) = a అనుకుందాం. అప్పుడు a ∈ A,
f(a) = f(g(a)) = I_B (b) = b కనుక f^-1 (b) = a
ఇందువల్ల అన్నీ b ∈ B కు
g(b) = f^-1(b) కాబట్టి g = f^-1

ప్రశ్న 28.
f : A → B, g : B → C లు ద్విగుణ ప్రమేయాలు అనుకుందాం. అప్పుడు (gof)^-1 = f^-1og^-1 అని నిరూపించుము. [Mar. ’14, ’11; May ’11]
సాధన:
f : A → B, g : B → C’ లు ద్విగుణ ప్రమేయాలు. కనుక A నుంచి B కి gof ద్విగుణ ప్రమేయం. అందువల్ల (gof)^-1, C నుంచి A కి ద్విగుణ ప్రమేయం, ఇంకా
f^-1 : B → A, g^-1 : C → B లు కూడా ద్విగుణ ప్రమేయాలు. అందువల్ల C నుంచి A కు f^-1og^-1 ద్విగుణ ప్రమేయం. (gof)^-1, f^-1og^-1 ప్రమేయాల ప్రదేశం C అవుతుంది.
C ∈ C అనుకుందాం. g^-1 (c) = b అనుకుందాం. అప్పుడు
b ∈ B, g(b) = c. f^-1 (b) = a అనుకుందాం. అప్పుడు
a ∈ A, f(a) = b.
(f^-1og^-1) (c) = f^-1(g^-1(c)) = f^-1(b) = a ………….. (1)
ఇంకా (gof) (a) = g(f(a)) = g(b) = c అందువల్ల
(gof)^-1 (c) = a …………… (2)
(1), (2) ల నుండి
(gof)^-1 (c) = (f^-1og^-1(c)
కనుక (gof)^-1 = f^-1og^-1