AP Inter 1st Year Maths 1B Important Questions Chapter 5 త్రిపరిమాణ నిరూపకాలు

Students get through AP Inter 1st Year Maths 1B Important Questions Chapter 5 త్రిపరిమాణ నిరూపకాలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1B Important Questions Chapter 5 త్రిపరిమాణ నిరూపకాలు

సాధించిన సమస్యలు

ప్రశ్న 1.
A(-4, 9, 6), B(-1, 6, 6), C(0, 7, 10) బిందువులు ఒక లంబకోణ సమద్విబాహు త్రిభుజాన్ని ఏర్పరుస్తాయని చూపండి.
సాధన:
A(-4, 9, 6), B(-1, 6, 6), C(0, 7, 10) లు ABC త్రిభుజ శీర్షాలు
AB = \(\sqrt{(-4+1)^2+(9-6)^2+(6-6)^2}\)
= \(\sqrt{9+9}\)
= \(\sqrt{18}\)
BC = \(\sqrt{(-1-0)^2+(6-7)^2+(6-10)^2}\)
= \(\sqrt{1+1+16}\)
= \(\sqrt{18}\)
CA = \(\sqrt{(0+4)^2+(7-9)^2+(10-6)^2}\)
= \(\sqrt{16+4+16}\)
= \(\sqrt{36}\)
AB = BC మరియు AB² + BC² = CA²
ABC లంబకోణ సమద్విబాహు త్రిభుజం

ప్రశ్న 2.
Y – అక్షం నుంచి ఒక బిందువు దూరం, (1, 2, -1) నుంచి దాని దూరానికి మూడు రెట్లయితే ఆ బిందువు బిందుపధం 8x² + 9y² + 8z² – 18x – 36y+ 18z + 54 = 0 అని చూపండి.
సాధన:
P (x, y, z) బిందుపధము మీది బిందువు
PM = Y – అక్షం నుండి దూరము = \(\sqrt{\mathrm{x}^2+\mathrm{z}^2}\)
A(1, 2, -1) దత్త బిందువు
దత్త నియమము PM = 3. PA
PM² = 9PA²
x² + z² = 9[(x – 1)² + (y – 2)² + (z + 1)²]
= 9x² – 18x + 9 + 9y² – 36y + 36 + 9z² + 18z + 9
P బిందువులు 8x² + 9y² + 8z² – 18x – 36y +18z + 54 = 0
P తృప్తి పరిచే సమీకరణము
8x² + 9y² + 8z² – 18x – 36y + 18z + 54 = 0

ప్రశ్న 3.
\(\overrightarrow{\mathrm{ox}}, \overrightarrow{\mathrm{oy}}, \overrightarrow{\mathrm{oz}}\) లపై మూల బిందువు నుంచి a, b, c (a ≠ 0, b ≠ 0, c ≠ 0) వరుసగా A, B, C లు. O, A, B, C ల నుంచి సమాన దూరాలలో ఉండే బిందువు పథాన్ని కనుక్కోండి.
సాధన:
A బిందువు ox మీద ఉంది
A నిరూపకాలు (a, 0, 0)
ఇదే విధంగా B నిరూపకాలు (0, b, c), C నిరూపకాలు (0, 0, c)
P(x, y, z) కావలసిన బిందువులు
PO = PA = PB = PC
PO² = PA² = PB² = PC²
PO² = PA²
x² + y² + z² = (x – a)² + y² + z²
x² – x² + a² – 2ax = 0
2ax = a² ⇒ a x = \(\frac{a^2}{2 a}=\frac{a}{2}\)
PO² = PB² ⇒ y = b/2
PO² = PC² ⇒ z = c/2
P నిరూపకాలు \(\left(\frac{a}{2}, \frac{b}{2}, \frac{c}{2}\right)\)

ప్రశ్న 4.
A (3,-2, 4), B(1, 1, 1), C(-1, 4, -2) బిందువులు సరేఖీయాలు అని చూపండి.
సాధన:
A (3, – 2, 4), B (1, 1, 1), C(-1, 4, -2) లు దత్త బిందువు
AB = \(\sqrt{(3-1)^2+(-2-1)^2+(4-1)^2}\)
= \(\sqrt{4+9+9}\)
= \(\sqrt{22}\)
BC = \(\sqrt{(1+1)^2+(1-4)^2+(1+2)^2}\)
= \(\sqrt{4+9+9}\)
= \(\sqrt{22}\)
AC = \(\sqrt{(3+1)^2+(-2-4)^2+(4+2)^2}\)
= \(\sqrt{16+36+36}\)
= \(\sqrt{88}\)
= 2\(\sqrt{22}\)
AB + BC = \(\sqrt{22}\) + \(\sqrt{22}\) = 2\(\sqrt{22}\) = AC
A, B, C లు సరేఖీయాలు

ప్రశ్న 5.
A(2, 4, 5), B(3, 5, 4) లను కలిపే సరళరేఖా ఖండాన్ని YZ – తలం విభజించే నిష్పత్తిని మరియు ఖండన బిందువును కనుక్కోండి.
సాధన:
AB రేఖ YZ తలాన్ని P వద్ద ఖండిస్తుంది.
P బిందువు AB ని k : 1 నిష్పత్తిలో విభజిస్తుంది.
P నిరూపకాలు
\(\left(\frac{3 k+2}{k+1}, \frac{5 k+4}{k+1}, \frac{-4 k+5}{k+1}\right)\)
P బిందువు YZ తలంపై ఉంది
⇒ p యొక్క X నిరూపకాలు
\(\frac{3 k+2}{k+1}\) = 0 ⇒ 3k + 2 = 0
k = – \(\frac{2}{3}\)
YZ తలం AB ని -2 : 3 నిష్పత్తిలో విభజిస్తుంది.
k విలువ p నిరూపకాలతో ప్రతిక్షేపించగా
p నిరూపకాలు
\(\left[0, \frac{5\left(-\frac{2}{3}\right)+4}{-\frac{2}{3}+1}, \frac{(-4)\left(-\frac{2}{3}\right)+5}{-\frac{2}{3}+1}\right]\)
(0, 2, 23)

ప్రశ్న 6.
A(3, -2, 4), B(1, 1, 1), C (-1, 4, -2) బిందువులు సరేఖీయాలని చూపండి.
సాధన:
P బిందువు AD ని k : 1 నిష్పత్తిలో విభజిస్తుందనుకుందాం.
P నిరూపకాలు \(\left(\frac{k+3}{k+1}, \frac{k-2}{k+1}, \frac{k+4}{k+1}\right)\)
అయితే A, B, C లు సరేఖీయాలు ( బిందువు AB మీద ఉంది. k ఏదైని విలువకు P నిరూపకాలు C లో ఏకీభవించవలెను.
\(\frac{k+3}{k+1}\) = -1 ⇒ k + 3 = -k – 1
2h = 4 ⇒ k = -2
k = -2 ప్రతిక్షేపిస్తే P నిరూపకాలు
\(\left(\frac{-2+3}{-2+1}, \frac{-2-2}{-2+1}, \frac{-2+4}{-2+1}\right)\)
= (-1, 4, -2) = c

ప్రశ్న 7.
A, B, C లు సరేఖీయాలు (2, 4, -1), (3, 6, −1), (4, 5, 1) వరుస శీర్షాలుగా గల సమాంతర చతుర్భుజం యొక్క నాలుగో శీర్షాన్ని కనుక్కోండి. [Mar. ’11]
సాధన:

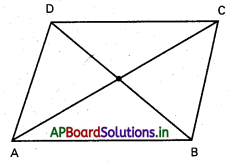
ABCD సమాంతర చతుర్భుజం.
A = (2, 4, -1), B – (3, 6, −1).
C = (4, 5, 1)
D(x, y, z) నాల్గవ శీర్షం
A B C D సమాంతర చతుర్భుజం
AC మధ్య బిందువు = BD మధ్య బిందువు
\(\left(\frac{2+4}{2}, \frac{4+5}{7}, \frac{-1+1}{2}\right)\) = \(\left(\frac{3+x}{2}, \frac{6+y}{2}, \frac{-1+z}{2}\right)\)
\(\frac{3+x}{2}\) = \(\frac{6}{2}\)
3 + x = 6
x = 3

\(\frac{6+y}{2}\) = \(\frac{9}{2}\)
6 + y = 9
y = 3

\(\frac{0}{2}\) = \(\frac{z-1}{2}\)
z – 1 = 0
z = 1
∴ నాల్గవ శీర్షం నిరూకాలు = D (3, 3, 1)

ప్రశ్న 8.
A(5,4, 6), B(1, -1, 3), C(4, 3, 2) అంతరాళంలో మూడు బిందువులు. ∠BAC యొక్క సమద్విఖండన రేఖ \(\overline{\mathrm{BC}}\) రేఖాఖండాన్ని ఖండించే బిందువు నిరూపకాలు కనుక్కోండి.
సాధన:
AB రేఖ ∠BAC కోణ సమద్విఖండనరేఖ అయితే D బిందువు BC ని AB : AC నిష్పత్తిలో విభజిస్తుంది.

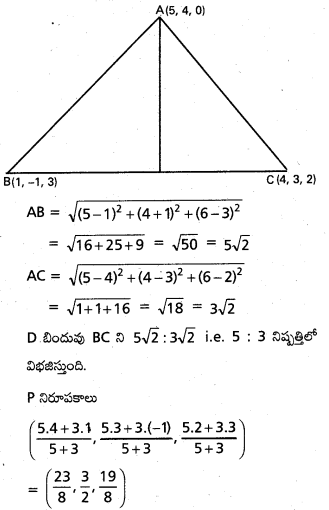
ప్రశ్న 9.
ఒక త్రిభుజం రెండు శీర్షాలు (x₁, y₁, z₁), (x₂, y₂, z₂) లు మరియు కేంద్రభాసం (α, β, γ) అయితే త్రిభుజం మూడో శీర్షాన్ని కనుక్కోండి.
సాధన:
A = (x₁, y₁, z₁), B = (x₂, y₂, z₂) లు త్రిభుజం ABC రెండు శీర్షాలనుకొందాం.

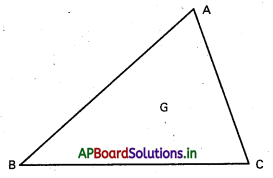
G = (α, β, γ) కేంద్రభాసం అనుకొందాం.
C = (x₃, y₃, z₃) మూడో శీర్షమైతే,.
\(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\) = (α, β, γ)
⇒x₁ + x₂ + x₃ = 3α; y₁ + y₂ + y₃ = 3β; z₁ + z₃ + z₃ = 3γ.
⇒ x₃ = 3α – x₁ – x₂; y₃ = 3β – y₁ – y₂; z₃ = 3γ – z₁ – z₂
∴ మూడో శీర్షం
C = (3α – x₁ – x₂, 3β – y₁ – y₂, 3γ – z₁ – z₂).

ప్రశ్న 10.
త్రిభుజం A, B, C భుజాలు BC, CA, AB ల మధ్య బిందువులు వరసగా D(x₁, y₁, z₁), E(x₂, y₂, z₂), F(x₃, y₃, z₃) లు అయితే శీర్షాలు A, B, C లను కనుక్కోండి.
సాధన:
BC భుజం మధ్య బిందువు D, CA భుజం మధ్య బిందువు E, AB భుజం మధ్య బిందువు F అని దత్తాంశం.

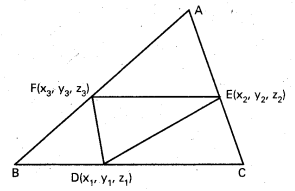
∴ DEF అనేది మధ్య బిందువులతో ఏర్పడిన త్రిభుజం.
AEDF సమాంతర చతుర్భుజాన్ని పరిగణిద్దాం.
A = (h, k, s) కనుక్కోవాల్సిన శీర్షం అనుకొందాం.
AD మధ్య బిందువు = EF మధ్యబిందువు
⇒ \(\left(\frac{h+x_1}{2}, \frac{k+y_1}{2}, \frac{s+z_1}{2}\right)\) = \(\left(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}, \frac{z_2+z_3}{2}\right)\)
⇒ h = x₂ + x₃ – x₁; k = y₂ + y₃ – y₂; s = z₂ + z₃ – z₁
∴ శీర్షం A = (x₂ + x₃ – x₁, y₂ + y₃ – y₁, z₂ + z₃ – z₁).
ఈ విధంగానే
శీర్షం B = (x₃ + x₁ – x₂, y₃ + y₁ – y₂, z₃ + z₁ – z₂)
శీర్షం C = (x₁ + x₂ − x₃, y₁ + y₂ – y₃, z₁ + z₂ – z₃).
లను రాబట్టవచ్చు.

ప్రశ్న 11.
A(x₁, y₁, z₁), B బిందువులను కలిపే రేఖాఖండం మధ్య బిందువు M(α, β, γ) అయితే B ని కనుక్కోండి.
సాధన:

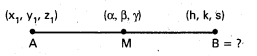
B(h, k, s) కనుక్కోవలసిన బిందువు అనుకొందాం.
AB మధ్య బిందువు M అనేది దత్తాంశం. కనుక
(α, β, γ) = \(\left(\frac{\mathrm{x}_1+\mathrm{h}}{2}, \frac{\mathrm{y}_1+\mathrm{k}}{2}, \frac{\mathrm{z}_1+\mathrm{s}}{2}\right)\)
⇒ 2α = x₁ + h; 2β = y₁ + k; 2γ = z₁ + s
⇒ h = 2α – x₁; k = 2β – y₁; s = 2γ – z₁
బిందువు B = (2α – x₁, 2β – y₁, 2γ – z₁).

ప్రశ్న 12.
(1, 2, 3), (2, 3, 1), (3, 1, 2) బిందువులతో ఏర్పడిన త్రిభుజం లంబకేంద్రం, కేంద్రభాసం, పరికేంద్రం, అంతరకేంద్రాలు వరసగా H, G, S, I లు అయితే వాటి విలువలను కనుక్కోండి.
సాధన:
AB = \(\sqrt{(2-1)^2+(3-2)^2+(1-3)^2}\)
= \(\sqrt{1+1+4}\)
= \(\sqrt{6}\)
BC = \(\sqrt{(3-2)^2+(1-3)^2+(2-1)^2}\)
= \(\sqrt{1+4+1}\)
= \(\sqrt{6}\)
CA = \(\sqrt{(1-3)^2+(2-1)^2+(3-2)^2}\)
= \(\sqrt{4+1+1}\)
= \(\sqrt{6}\)

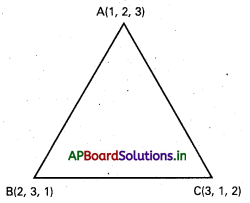
AB = BC = CA కాబట్టి, ABC సమబాహు త్రిభుజం.
కేంద్రభాసం G = \(\left(\frac{1+2+3}{3}, \frac{2+3+1}{3}, \frac{3+1+2}{3}\right)\) = (2, 2, 2)
సమబాహు త్రిభుజంలో లంబకేంద్రం, కేంద్రభాసం, పరికేంద్రం, అంతరకేంద్రాలు సమానం (నాలుగు బిందువులు ఏకీభవిస్తాయి).
కాబట్టి H = ( 2, 2, 2), S = (2, 2, 2), I = (2, 2, 2)

ప్రశ్న 13.
(0, 0, 0), (3, 0, 0), (0, 4, 0)లతో ఏర్పడిన త్రిభుజం అంతర కేంద్రం కనుక్కోండి.
సాధన:
A = (x₁, y₁, z₁), B = (x₂, y₂, z₂), C = (x₃, y₃, z₃) లు శీర్షాలుగా గల ABC త్రిభుజం భుజాలు a, b, c అయితే త్రిభుజం అంతరకేంద్రం

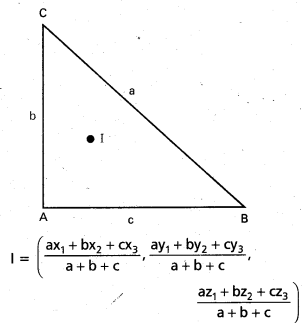
A = (0, 0, 0), B = (3, 0, 0), C (0, 4, 0).
a = BC = \(\sqrt{9+16+0}\) = 5;
b = CA = \(\sqrt{0+16+0}\) = 4;
c = AB = \(\sqrt{9+0+0}\) = 3;
కాబట్టి I = \(\frac{5(0)+4(3)+3(0)}{5+4+3}, \frac{5(0)+4(0)+3(4)}{5+4+3}, \left.\frac{5(0)+4(0)+3(0)}{5+4+3}\right)\)
= (1, 1, 0)

ప్రశ్న 14.
సమాంతర అక్షపరివర్తనం ద్వారా (1, 2, 3) బిందువును (2, 3, 1) బిందువు వద్దకు మారిస్తే, నూతన మూల బిందువును కనుక్కోండి.
సాధన:
Oxyz నిరూపక వ్యవస్థ దృష్ట్యా P బిందువు నిరూపకాలు (x, y, z) అనుకొందాం. O’XYZ నిరూపక వ్యవస్థ దృష్ట్యా P
బిందువు నిరూపకాలు (X,Y,Z) అనుకొందాం.

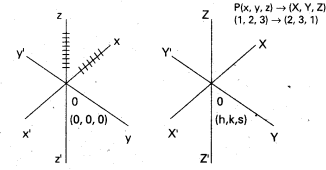
O’ (h, k, s) నూతన మూలబిందువు అయితే
X = X + h‚ y = Y + k, z = Z + s అవుతాయి.
⇒ (h, k, s) (x – X, y – Y, z – Z)
⇒ (h, k, s) = (1 – 2, 2 – 3, 3 – 1)
= (-1, -1, 2).
∴ O’ = (-1, -1, 2) నూతన మూలబిందువు.

ప్రశ్న 15.
A(3, 2, -4), B(9, 8, -10) బిందువులను కలిపే రేఖాఖండాన్ని P(5, 4, -6) బిందువు విభజించే నిష్పత్తి కనుక్కోండి. ఇంకా P హరాత్మక సంయుగ్మ బిందువును కూడా’ కనుక్కోండి.
సాధన:

AB రేఖా ఖండాన్ని P బిందువు విభజించే నిష్పత్తి l : m అనుకొందాం.
∴ (5, 4, -6)
= \(\left(\frac{9 l+3 \mathrm{~m}}{l+\mathrm{m}}, \frac{8 l+2 \mathrm{~m}}{l+\mathrm{m}}, \frac{-10 l-4 \mathrm{~m}}{l+\mathrm{m}}\right)\)
⇒ l : m = 1 : 2 లేదా 2l = m.
AB ని Q బిందువు l : – m నిష్పత్తిలో విభజిస్తుందనుకొందాం. అప్పుడు
Q = \(\left(\frac{9 l-3 \mathrm{~m}}{l-\mathrm{m}}, \frac{8 l-2 \mathrm{~m}}{l-\mathrm{m}}, \frac{-10 l+4 \mathrm{~m}}{l-\mathrm{m}}\right)\)
= \(\left(\frac{9 l-6 l}{l-2 l}, \frac{8 l-4 l}{l-2 l}, \frac{-10 l+8 l}{l-2 l}\right)\)
= (-3, -4, 2)
∴ P(5, 4, -6) హరాత్మక సంయుగ్మ బిందువు Q(-3, -4, 2).