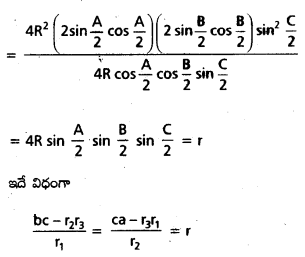AP Inter 1st Year Maths 1A Important Questions Chapter 10 త్రిభుజ ధర్మాలు

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 10 త్రిభుజ ధర్మాలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 10 త్రిభుజ ధర్మాలు

సాధించిన సమస్యలు
(Solved Problems)

ప్రశ్న 1.
ΔABC లో a = 3, b = 4, sin A = \(\frac{3}{4}\) అయితే, B కోణాన్ని ‘కనుక్కోండి.
సాధన:
సైను సూత్రం నుంచి \(\frac{a}{\sin A}\) = \(\frac{b}{\sin B}\)
⇒ sin B = \(\frac{\text { b. } \sin A}{a}\) = \(\frac{4}{3} \cdot\left(\frac{3}{4}\right)\) = 1
⇒ sin B = 1 ⇒ B = 90°

ప్రశ్న 2.
ఒక త్రిభుజం భుజాల పొడవులు 3, 4, 5 అయితే, ఆ త్రిభుజ పరివృత్త వ్యాసార్థాన్ని కనుక్కోండి.
సాధన:
∵ 3² + 4² = 5²
∴ కనుక త్రిభుజం లంబకోణ త్రిభుజం.
దాని కర్ణం = 5 = పరివృత్త వ్యాసం
∴ పరివృత్త వ్యాసార్థం = \(\frac{1}{2}\)(కర్ణం) = \(\frac{5}{2}\) సెం.మీ.

ప్రశ్న 3.
a = 6, b = 5, c = 9 అయితే A, కోణాన్ని కనుక్కోండి.
సాధన:
∵ cos A = \(\frac{b^2+c^2-a^2}{2 b c}\)(కోసైను సూత్రం)
= \(\frac{5^2+9^2-6^2}{2(5)(9)}\) = \(\frac{25+81-36}{2(5)(9)}\)
= \(\frac{70}{90}\) = \(\frac{7}{9}\)

ప్రశ్న 4.
ΔABC లో Σ(b + c) cos A = 2s అని చూపండి.
సాధన:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + c cos A) + (c cos B + a cos B) + (a cos C + b cos C)
= (b cos C + c cos B) + (a cos C + ccos A) + (a cos B + b cos A)
= a + b + c = R.H.S.

ప్రశ్న 5.
త్రిభుజ భుజాలు 13, 14, 15 అయినప్పుడు, పరివృత్త వ్యాసాన్ని కనుక్కోండి.
సాధన:
a = 13, b = 14, c = 15
2s = a + b + c = \(\frac{13+14+15}{2}\) = \(\frac{42}{2}\)
∴ s = 21
s – a = 21 – 13 = 8
s – b = 21 – 14 = 7
s – c = 21 – 15 = 6
Δ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{21 \times 8 \times 7 \times 6}\)
= \(\sqrt{21 \times 21 \times 16}\) = 21 × 4 = 84
∴ Δ = \(\frac{a b c}{4 R}\)
⇒ 4R = \(\frac{a b c}{\Delta}\) = \(\frac{13 \times 14 \times 15}{84}\) = \(\frac{65}{2}\)
∴ R = \(\frac{65}{8}\)
∴ పరివృత్త వ్యాసం (2R) = 2′ × \(\frac{65}{8}\) = \(\frac{65}{4}\) సెం. మీ

ప్రశ్న 6.
ΔABC s, (a + b + c) (b + c − a) = 3abc, అయితే A ని కనుక్కోండి.
సాధన:
(a + b + c) (b + c − a) = 3bc
⇒ [(b + c) + a] [(b + c) – a] = 3bc
⇒ (b + c)² – a² = 3bc
⇒ b² + c² + 2bc – a² = 3bc
⇒ b² + c² – a² = bc
⇒ \(\frac{b^2+c^2-a^2}{2 b c}\) = \(\frac{1}{2}\)
⇒ cos A = \(\frac{1}{2}\) = 60°
A = 60°

ప్రశ్న 7.
a = 4, b = 5, c = 7 అయితే cos \(\frac{B}{2}\) కనుక్కోండి.
సాధన:
2s = a + b + c = 4 + 5 + 7 = 16
⇒ s = 8, s – b = 8 – 5 = 3
cos \(\frac{\mathrm{B}}{2}\) = \(\sqrt{\frac{s(s-b)}{a c}}\) = \(\sqrt{\frac{8 \times 3}{4 \times 7}}\) = \(\sqrt{\frac{6}{7}}\)

ప్రశ్న 8.
ΔABC లో, b cos² \(\frac{C}{2}\) + c cos² \(\frac{B}{2}\) ను కనుక్కోండి.
సాధన:
b cos² \(\frac{C}{2}\) + c cos² \(\frac{B}{2}\)= b.
= \(\text { b. } \frac{s(s-c)}{a b}\) + \(\text { c. } \frac{s(s-b)}{c a}\)
= \(\frac{s(s-c)}{a}\) + \(\frac{s(s-b)}{a}\) = \(\frac{s}{a}\)(s – c + s – b)
= \(\frac{s}{a}\)(a + b + c − c − b) = \(\frac{s}{a} a\) = s

ప్రశ్న 9.
tan \(\frac{A}{2}\) = \(\frac{5}{6}\), tan \(\frac{C}{2}\) = \(\frac{2}{5}\) అయితే a, b, c ల మధ్య సంబంధాన్ని నిర్ధారించండి. (May 05)
సాధన:
tan \(\frac{A}{2}\). tan \(\frac{C}{2}\) = \(\frac{5}{6}\). \(\frac{2}{5}\)
\(\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \sqrt{\frac{(s-a)(s-b)}{s(s-c)}}\) = \(\frac{2}{6}\)
⇒ \(\frac{s-b}{s}\) = \(\frac{1}{3}\) ⇒ 3s – 3b = s ⇒ 2s = 3b
⇒ a + b + c = 3b ⇒ a + c = 2b
a, b, c లు A.P.లో ఉన్నవి

ప్రశ్న 10.
cot \(\frac{A}{2}\) = \(\frac{\mathbf{b}+\mathbf{c}}{\mathbf{a}}\), అయితే, B కోణాన్ని కనుక్కోండి.
సాధన:

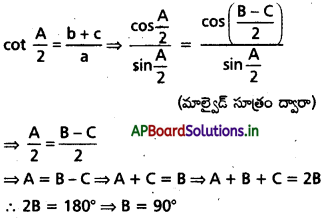
ప్రశ్న 11.
tan \(\left(\frac{\mathbf{C}-\mathbf{A}}{2}\right)\) = k cot \(\frac{\mathrm{B}}{2}\) అయితే, k ని కనుక్కోండి.
సాధన:
టాంజంట్ సూత్రం నుంచి
tan \(\left(\frac{\mathrm{C}-\mathrm{A}}{2}\right)\) = \(\left(\frac{c-a}{c+a}\right)\) cot \(\frac{B}{2}\)
కనుక k = \(\frac{c-a}{c+a}\)

ప్రశ్న 12.
ΔABC లో \(\frac{\mathbf{b}^2-\mathbf{c}^2}{\mathbf{a}^2}\) = \(\frac{\sin (B-C)}{\sin (B+C)}\) అని చూపండి.
సాధన:

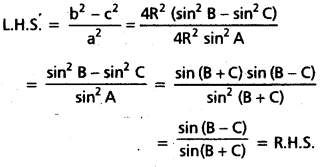
ప్రశ్న 13.
a² cot A + b² cot B + c² cot C = \(\frac{a b c}{\mathbf{R}}\) అని చూపండి. (Mar. 14)
సాధన:
L.H.S. = a² cot A + b² cot B + c² cot C
= 4R² sin² A. \(\frac{\cos A}{\sin A}\) + 4R² sin²B. \(\frac{\cos B}{\sin B}\) + 4R² sin² C. \(\frac{\cos C}{\sin C}\) (సైను సూత్రం ద్వారా)
= 2R² (2 sin A cos A + 2 sin B cos B + 2 sin C cos C)
= 2R² (sin 2A + sin 2B + sin 2C)
= 2R² (4 sin A sin B sin C) (సర్వ సమానతల నుంచి)
= \(\frac{1}{R}\)(2R sin A) (2R sin B) (2R sin C)
= \(\frac{a b c}{R}\) = R.H.S.

ప్రశ్న 14.
(b – c)² cos² \(\frac{A}{2}\) + (b + c)² sin² \(\frac{A}{2}\) = a² అని చూపండి.
సాధన:
L.H.S. = (b² + c² – 2bc) cos² \(\frac{A}{2}\) + (b² + c² + 2bc) sin² \(\frac{A}{2}\)
= (b² + c²) [cos² \(\frac{A}{2}\) + sin² \(\frac{A}{2}\)] – 2bc (cos² \(\frac{A}{2}\) – sin² \(\frac{A}{2}\)) = b² + c² – 2bc cos A
= a²

ప్రశ్న 15.
a (b cos c – c cos B) = b² – c² అని చూపండి. (Mar. 07)
సాధన:
L.H.S. = ab cos C – ca cos B
= \(\left(\frac{a^2+b^2-c^2}{2}\right)\) – \(\left(\frac{c^2+a^2-b^2}{2}\right)\)
కోనైన్ సూత్రం నుంచి
= \(\frac{1}{2}\)[a² + b² – c² – c² – a² + b²]
= b² – c² = R.H.S.

ప్రశ్న 16.
\(\frac{c-b \cos A}{b-c \cos A}\) = \(\frac{\cos B}{\cos C}\) -అని చూపండి.
సాధన:
లంబవిక్షేప సూత్రం నుంచి
c = a cos B + b cos A
b = c cos A + a cos C

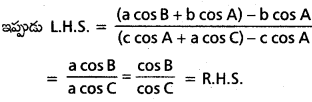
ప్రశ్న 17.
ΔABC లో, \(\frac{1}{a+c}\) + \(\frac{1}{b+c}\) = \(\frac{3}{a+b+c}\) అయితే, C = 60° అని చూపండి.
సాధన:
\(\frac{1}{a+c}\) + \(\frac{1}{b+c}\) = \(\frac{3}{a+b+c}\)
⇒ \(\frac{b+c+a+c}{(a+c)(b+c)}\) = \(\frac{3}{a+b+c}\)
⇒ 3(a + c) (b + c) = (a + b + 2c) (a + b + c)
⇒ 3(ab + ac + bc + c²) = (a² + b² + 2ab) + 3c(a + b) + 2c²
⇒ ab = a² + b² – c²
⇒ ab = a² + b² – c²
= 2ab cos C (కోసైను సూత్రం నుంచి)
⇒ cos C = \(\frac{1}{2}\) ⇒ C = 60°

ప్రశ్న 18.
a = (b – c) sec θ అయితే, tan θ = \(\frac{2 \sqrt{b c}}{b-c}\) sin \(\frac{\mathbf{A}}{2}\) అని రుజువు చేయండి.
సాధన:
a = (b – c) sec θ ⇒ sec θ = \(\frac{a}{b-c}\)

ప్రశ్న 19.
ΔABC లో (a + b + c) (tan \(\frac{A}{2}\) + tan \(\frac{B}{2}\)) = 2c cot \(\frac{C}{2}\) అని చూపండి.
సాధన:

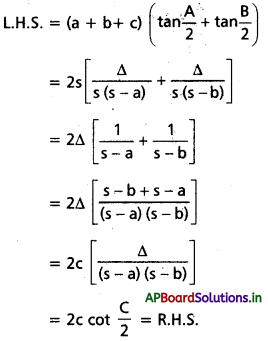
ప్రశ్న 20.
b² sin 2C + c² sin 2B = 2bc sin A అని చూపండి.
సాధన:
L.H.S. = b² sin 2C + c² sin 2B
= 4R² sin2 B (2 sin C cos C) + 4R² sin² C (2 sin B cos B)
= 8R² sin B sin C (sin B cos C + cos B sin C)
= 8R² sin B sin C sin (B + C)
= 2(2R sin B) (2R sin C) sin A
= 2bc sin A
= R.H.S.

ప్రశ్న 21.
cot A + cot B + cot C = \(\frac{a^2+b^2+c^2}{4 \Delta}\) అని రుజువు చేయండి. ((T.S) Mar. 15)
సాధన:

ప్రశ్న 22.
a cos² \(\frac{A}{2}\) + b cos² \(\frac{B}{2}\) + c cos² \(\frac{C}{2}\) = s + \(\frac{\Delta}{\mathbf{R}}\)
సాధన:

ప్రశ్న 23.
ΔABC లో a cos A = b cos B అయితే, త్రిభుజం సమద్విబాహు లేదా లంబకోణ త్రిభుజమని రుజువు చేయండి.
సాధన:
a cos A = b cos B
⇒ 2R sin A cos A = 2R sin B cos B
⇒ sin 2A = sin 2B (or) = sin (180° – 2B)
కనుక 2A = 2B లేదా 2A = 180° – 2B
⇒ A = B లేదా A = 90° – B
⇒ A = B లేదా A + B = 90°
⇒ C = 90°
∴ త్రిభుజం సమద్విబాహు లేదా లంబకోణ త్రిభుజం.

ప్రశ్న 24.
cot \(\frac{\mathbf{A}}{2}\) : cot \(\frac{\mathbf{B}}{2}\) : cot \(\frac{\mathbf{C}}{2}\) = 3 : 5 : 7 అని చూపండి
సాధన:

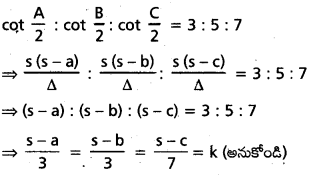
అప్పుడు s – a = 3k, s – b = 5k, s – c = 7k
కలుపగా 3s – (a + b + c) = 3k + 5k + 7k
⇒ 3s – 2s = 15k ⇒ s = 15k
ఇప్పుడు a = 12k, b = 10k, c = 8k
∴ a : b : c = 12k : 10k : 8k = 6 : 5 : 4

ప్రశ్న 25.
a³ cos (B – C) + b³ cos (C – A) + C³ cos (A – B) = 3abc అని రుజువు చేయండి.
సాధన:
L.H.S. = Σa³ cos (B – C)
= Σa² (2R sin A)cos(B – C)
= R Σa² [2 sin (B + C) cos (B – C)]
= R Σa² (sin 2B + sin 2C)
= R Σa² (2 sin B cos B + 2 sin C cos C)
= Σ[a²(2R sin B) cos B + a²(2R sin C) cos C]
= Σ(a² b cos B + a²c cos C)
= (a²b cos B + a² c cos C) + (b²c cos C + b² a cos A) + (c² a cos A + c²b cos B)
= ab (a cos B + b cos A) + bc (b cos C + c cos B) + ca (c cos A + a cos C)
= ab(c) + bc(a) + ca(b) = 3 abc = R.H.S.

ప్రశ్న 26.
p₁, p₂, p₃ లు వరుసగా త్రిభుజ శీర్షాలు A,B, C ల ఉన్నతులయితే \(\frac{1}{p_1^2}\) + \(\frac{1}{p_2^2}\) + \(\frac{1}{p_3^2}\) = \(\frac{\cot A+\cot B+\cot C}{\Delta}\) అని చూపండి
సాధన:

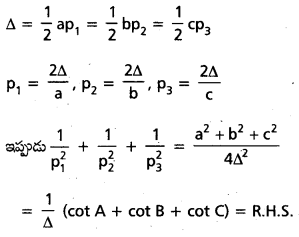
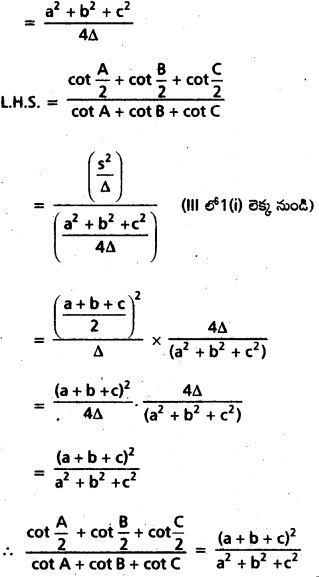
ప్రశ్న 27.
h ఎత్తు గల ఊర్ధ్వంగా ఉండే ఒక స్తంభం PQ పాదం Q గుండా పోయే క్షితిజ రేఖపై A అనే బిందువు నుంచి శిఖర బిందువు P కి ఊర్ధ్వ కోణం 45°. AQ తో 30° కోణం చేసే రేఖపై A నుండి 30 మీటర్ల దూరంలో B అనే బిందువు నుండి P ఊర్థ్వ కోణం 60° అయితే స్తంభం ఎత్తు కనుక్కోండి.
సాధన:

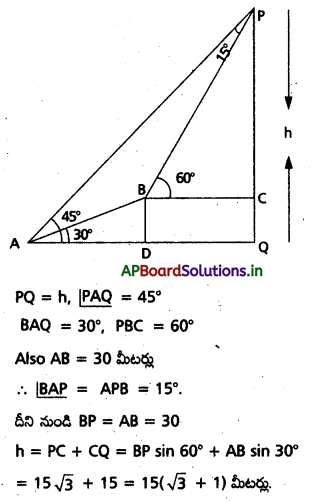
ప్రశ్న 28.
ఒక నదికి ఒకేవైపున A, B అనే రెండు చెట్లు ఉన్నాయి. నదిలో C అనే బిందువు నుండి A, B లు వరసగా 250 మీ. 300 మీ. దూరంలో ఉన్నాయి. C వద్ద కోణం 45° అయితే ఆ చెట్ల మధ్య దూరాన్ని కనుక్కోండి. (\(\sqrt{2}\) = 1.414).
సాధన:
త్రిభుజం ABC నుండి కొసైన్ రూలు ఉపయోగించగా

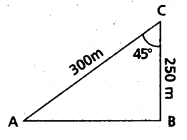
AB² = 250² + 300² – 2(250) (300) cos 45°
= 100 (625 + 900 – 750\(\sqrt{2}\)) = 46450.
∴ AB = 215.5 మీ. (ఉజ్జాయింపు)

ప్రశ్న 29.
ΔABC, లో \(\frac{1}{r_1}\) + \(\frac{1}{r_2}\) + \(\frac{1}{r_3}\) = \(\frac{1}{r}\) అని రుజువు చేయండి.
సాధన:

ప్రశ్న 30.
rr₁ r₂ r₃ = Δ² అని చూపండి.
సాధన:

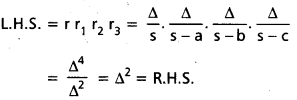
ప్రశ్న 31.
సమబాహు త్రిభుజంలో \(\frac{r}{R}\) విలువను కనుక్కోండి.
సాధన:

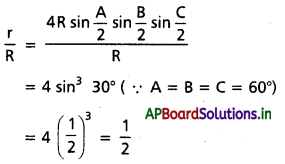
ప్రశ్న 32.
ΔABC చుట్టుకొలత 12 సెం.మీ. దీని అంతర వ్యాసార్థం 1 సెం.మీ. అప్పుడు త్రిభుజ వైశాల్యాన్ని కనుక్కోండి.
సాధన:
2s = 12 ⇒ s = 6 సెం.మీ.
r = 1 సెం.మీ.
ΔABC వైశాల్యము = Δ = rs = (1) (6) = 6 చ. సెం.మీ.

ప్రశ్న 33.
rr₁ = (s – b) (s – c)
సాధన:
L.H.S. = rr₁
= [(s – b) tan \(\frac{\mathrm{B}}{2}\)] [(s – c) cot \(\frac{\mathrm{B}}{2}\)]
= (s – b) (s – c) = R.H.S.

ప్రశ్న 34.
\(\frac{a \cos \mathbf{A}+\mathbf{b} \cos \mathbf{B}+\cos \mathbf{C}}{\mathbf{a}+\mathbf{b}+\mathbf{c}}\) ని R, r పదాలలో వ్యక్తపరచండి.
సాధన:

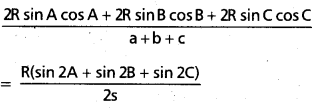
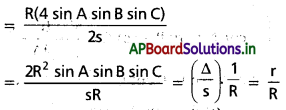
ప్రశ్న 35.
ΔABC లో Δ = 6 చ. సెం. మీ, s = 1.5 సెం. మీ అయితే F ను కనుక్కోండి.
సాధన:
r = \(\frac{\Delta}{\mathrm{s}}\) = \(\frac{6}{1.5}\) = 4 సెం.మీ.

ప్రశ్న 36.
rr₁ cot \(\frac{A}{2}\) = Δ అని చూపండి.
సాధన:
rr₁ cot \(\frac{A}{2}\) = \(\frac{\Delta}{s}\left(s \tan \frac{A}{2}\right)\) cot \(\frac{A}{2}\) = Δ

ప్రశ్న 37.
a = 13, b = 14, c = 15 అయితే r₂ ను కనుక్కోండి.
సాధన:
2s = a + b + c = 42
⇒ s = 21
s – a = 8, s – b = 7, s – c = 6
Δ² = 21 × 8 × 7 × 6
⇒ A = 7 × 12 = 84 చ. యూనిట్లు

ప్రశ్న 38.
rr₂ = r₁r₃ అయితే, B కనుక్కోండి.
సాధన:

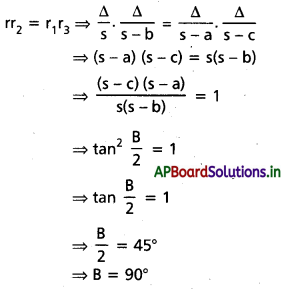
ప్రశ్న 39.
ΔABC లో భుజాలు a, b, c లు A.P.లో ఉండటానికి r₁, r₂, r₃ లు H.P. లో ఉండాలనేది ఆవశ్యక, పర్యాప్త
నియమమని చూపండి.
సాధన:
r₁,r₂, r₃ లు H.P. లో ఉన్నాయి.
⇔ \(\frac{1}{r_1}\), \(\frac{1}{r_2}\), \(\frac{1}{r_3}\) లు A.P. లో ఉంటాయి.
⇔ \(\frac{s-a}{\Delta}\), \(\frac{s-b}{\Delta}\), \(\frac{s-c}{\Delta}\) లు A.P. లో ఉంటాయి.
⇔ s – a, s – b, s – c లు A.P. లో ఉంటాయి.
⇔ -a, -b, -c లు A.P. లో ఉంటాయి.
⇔ a, b, c లు A.P. లో ఉంటాయి.

ప్రశ్న 40.
A = 90° అయితే 2(r + R) = b + c అని చూపండి.
సాధన:
L.H.S= 2r+ 2R
= 2(s – a) tan \(\frac{A}{2}\) + 2R. 1
= 2(s – a) tan 45° + 2R sin A (∵ A = 90°)
= (2s – 2a). 1 + a
= b + c = R.H.S.

ప్రశ్న 41.
(r₂ – r₁) (r₃ – r₁) = 2r₂r₃ అయితే A = 90°
అని చూపండి.
సాధన:

ప్రశ్న 42.
\(\frac{r_1\left(r_2+r_3\right)}{\sqrt{r_1 r_2+r_2 r_3+r_3 r_1}}\) = a అని రుజువు చేయండి.
సాధన:

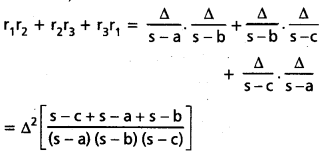
ప్రశ్న 43.
\(\frac{1}{r^2}\) + \(\frac{1}{r_1^2}\) + \(\frac{1}{r_2^2}\) + \(\frac{1}{r_3^2}\) = \(\frac{a^2+b^2+c^2}{\Delta^2}\)
సాధన:

ప్రశ్న 44.
Σ(r + r₁) tan \(\left(\frac{\mathbf{B}-\mathbf{C}}{2}\right)\) = 0 అని రుజువు చెయ్య౦డి
సాధన:

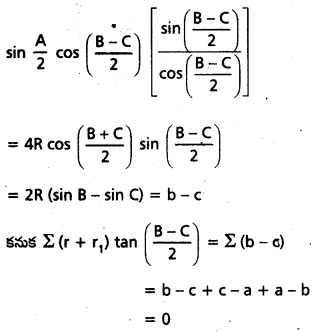
ప్రశ్న 45.
\(\frac{r_1}{b c}\) + \(\frac{r_2}{c a}\) + \(\frac{r_3}{a b}\) = \(\frac{1}{r}\)
– \(\frac{1}{2 R}\) అని చూపండి.
సాధన:

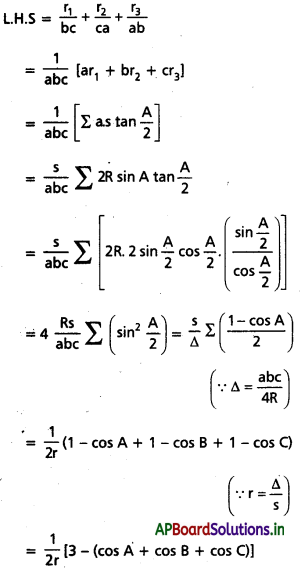
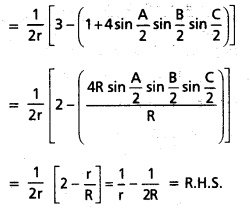
ప్రశ్న 46.
r : R : r₁ = 2 : 5 : 12 అయితే, ఆ త్రిభుజంలో A లంబకోణమని రుజువు చేయండి.
సాధన:
r: R: r₁ = 2 : 5 : 12
అప్పుడు r = 2k, R = 5k, r₁ = 12K
r₁ – r = 12k – 2k = 10k = 2(5k) = 2R
⇒ 4R sin \(\frac{A}{2}\)[cos \(\frac{B}{2}\)cos \(\frac{C}{2}\) – sin \(\frac{B}{2}\)sin \(\frac{C}{2}\)] = 2R

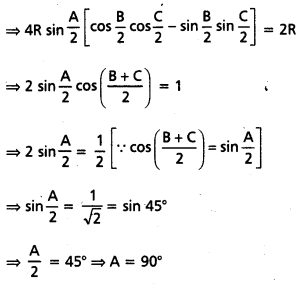
కనుక త్రిభుజములో A లంబకోణం.

ప్రశ్న 47.
r + r₃ + r₁ – r₂ = 4R cos B అని చూపండి. (Mar. ’13)
సాధన:

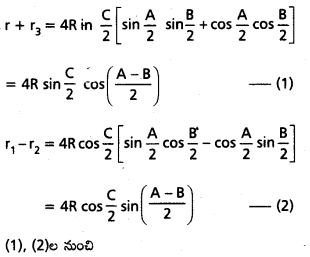
ప్రశ్న 48.
A, A₁, A₂, A₃ లు వరుసగా త్రిభుజ అంతరవృత్త, బాహ్య వృత్త వైశాల్యాలయితే \(\frac{1}{\sqrt{A_1}}\) + \(\frac{1}{\sqrt{A_2}}\) + \(\frac{1}{\sqrt{A_3}}\) = \(\frac{1}{\sqrt{A}}\) అని రుజువు చేయండి.
సాధన:
r, r₁, r₂, r₃ లు వరుసగా అంతర, బాహ్య వృత్త వ్యాసార్థాలు, వాటి వైశాల్యాలు A, A₁, A₂, A₃ లు అయితే

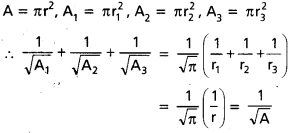
ప్రశ్న 49.
(r₁ + r₂) sec² \(\frac{C}{2}\) = (r₂ + r₃) sec² \(\frac{A}{2}\) = (r₃ + r₁) sec²\(\frac{B}{2}\) అని చూపండి.
సాధన:

ప్రశ్న 50.
ΔABC లో AD, BE, CF లు A, B, C శీర్షాల నుంచి ఎదుటి భుజాలకు గీచిన లంబాలయితే
i) \(\frac{1}{A D}\) + \(\frac{1}{B E}\) + \(\frac{1}{C F}\) = \(\frac{1}{r}\)
ii) AD. BE. CF = \(\frac{(a b c)^2}{8 R^3}\) అని చూపండి.
సాధన:

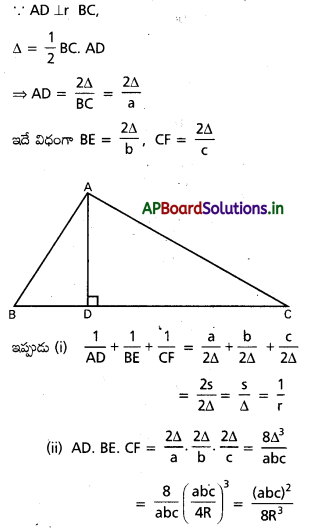
ప్రశ్న 51.
ΔABC లో r₁ = 8, r₂ = 12, r₃ = 24 అయితే a, b, c లను కనుక్కోండి. (May ’13)
సాధన:
∵ \(\frac{1}{r}\) = \(\frac{1}{r_1}\) + \(\frac{1}{r_2}\) + \(\frac{1}{r_3}\)
⇒ \(\frac{1}{r}\) = \(\frac{1}{8}\) + \(\frac{1}{12}\) + \(\frac{1}{24}\)
⇒ \(\frac{1}{r}\) = \(\frac{3+2+1}{24}\)
⇒ r = 4
కానీ Δ² = = rr₁r₂r₃ = 4 × 8 × 12 × 24
= (8 × 12)²

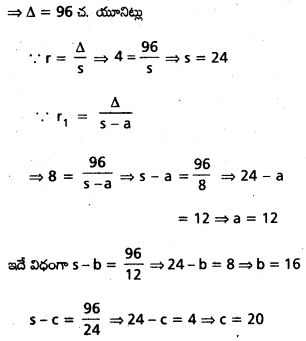
ప్రశ్న 52.
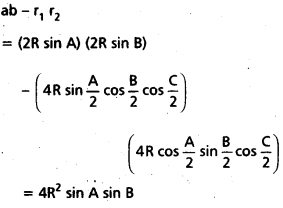
\(\frac{a b-r_1 r_2}{r_3}\) = \(\frac{b c-r_2 r_3}{r_1}\) = \(\frac{c a-r_3 r_1}{r_2}\) అని చూపండి. (Mar. ’08; May ’06)
సాధన: