AP Inter 1st Year Maths 1A Solutions Chapter 5 సదిశల గుణనం Ex 5(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 5 సదిశల గుణనం Exercise 5(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 5 సదిశల గుణనం Exercise 5(a)

I.

Question 1.
\(\overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}}, \mathbf{3} \overline{\mathbf{i}}-\overline{\mathbf{j}}+\mathbf{2} \overline{\mathbf{k}}\) సదిశల మధ్య కోణాన్ని కనుక్కోండి. [Mar. ’14]
Solution:

Question 2.
\(\mathbf{2} \overline{\mathbf{i}}+\lambda \overline{\mathbf{j}}-\overline{\mathbf{k}}, \mathbf{4} \overline{\mathbf{i}}-\mathbf{2} \overline{\mathbf{j}}+\mathbf{2} \overline{\mathbf{k}}\) సదిశలు పరస్పరం లంబంగా ఉంటే, λ విలువను కనుక్కోండి. [Mar. ’05; May ’05]
Solution:
\(\overline{\mathrm{a}}=2 \overline{\mathrm{i}}+\lambda \overline{\mathrm{j}}-\overline{\mathrm{k}}, \overline{\mathrm{b}}=4 \overline{\mathrm{i}}-2 \overline{\mathrm{j}}+2 \overline{\mathrm{k}}\) అనుకుందాం.
∵ \(\bar{a}, \bar{b}\) లు పరస్పరం లంబంగా ఉన్నవి.
⇒ \(\bar{a} \cdot \bar{b}\) = 0
⇒ \((2 \bar{i}+\lambda \bar{j}-\bar{k}) \cdot(4 \bar{i}-2 \bar{j}+2 \bar{k})\) = 0
⇒ (2) (4) + λ(-2) + (-1) (2) = 0
⇒ 8 – 2λ – 2 = 0
⇒ 2λ = 6
⇒ λ = 3

Question 3.
λ యొక్క ఏ విలువలకు \(\overline{\mathbf{i}}-\lambda \overline{\mathbf{j}}+2 \overline{\mathbf{k}}, 8 \overline{\mathbf{i}}+6 \overline{\mathbf{j}}-\overline{\mathbf{k}}\) సదిశలు లంబంగా ఉంటాయి?
Solution:
\(\bar{a}=\overline{\mathrm{i}}-\lambda \overline{\mathrm{j}}+2 \overline{\mathrm{k}}, \overline{\mathrm{b}}=8 \overline{\mathrm{i}}+6 \overline{\mathrm{j}}-\overline{\mathrm{k}}\)
∵ \((\bar{a}, \bar{b})=90^{\circ}\)
⇒ \(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}\) = 0
⇒ \((\bar{i}-\lambda \bar{j}+2 \bar{k}) \cdot(8 \bar{i}+6 \bar{j}-\bar{k})=0\)
⇒ 8 – (λ) (6) + 2(-1) = 0
⇒ 6 – 6λ = 0
⇒ λ = 1

Question 4.
\(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}-\mathbf{3} \overline{\mathbf{j}}-\mathbf{5} \overline{\mathbf{k}} \cdot \overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు త్రిభుజ భుజాలుగా రూపొందేటట్లు \(\bar{c}\) ను కనుక్కోండి.
Solution:

Question 5.
\(\bar{r} \cdot(2 \bar{i} \cdot-\bar{i}+2 \bar{k})=3 ; \bar{r} \cdot(3 \bar{i}-6 \bar{i}+\bar{k})=4\) తలాల మధ్యకోణం కనుక్కోండి. [(T.S) Mar. ’15]
Solution:

Question 6.
యూనిట్ సదిశలు \(\overline{\mathrm{e}}_1, \overline{\mathrm{e}}_2\) ల మధ్య కోణం θ అయి, \(\frac{1}{2}\left|\overline{\mathrm{e}}_1, \overline{\mathrm{e}}_2\right|\) = sin λθ అయితే, λ విలువను కనుక్కోండి.
Solution:
\(\overline{\mathrm{e}}_1, \overline{\mathrm{e}}_2\) లు యూనిట్ సదిశలు

Question 7.
\(\bar{a}=\bar{i}+\bar{i}+\bar{k}, \bar{b}=2 \bar{i}+3 \bar{i}+\bar{k}\) అనుకొందాం. అప్పుడు
(i) \(\overline{\mathbf{a}}\) పై \(\overline{\mathbf{b}}\) యొక్క లంబ విక్షేప సదిశను, దాని పరిమాణాన్ని కనుక్కోండి. [May ’13]
(ii) \(\overline{\mathbf{a}}\) దిశలోనూ \(\overline{\mathbf{a}}\) కి లంబ దిశలోను \(\overline{\mathbf{b}}\) యొక్క సదిశ అంశాలను కనుక్కోండి. [May ’06]
Solution:

Question 8.
(3, -2, 1) బిందువు గుండాపోతూ (4, 7, -4) సదిశకు లంబంగా ఉండే తలం సమీకరణం కనుక్కోండి. [(T.S) Mar. ’15]
Solution:

Question 9.
\(\overline{\mathrm{a}}=2 \overline{\mathrm{i}}+2 \overline{\mathrm{i}}-3 \overline{\mathrm{k}}, \overline{\mathrm{b}}=3 \overline{\mathrm{i}}-\overline{\mathrm{i}}+2 \overline{\mathrm{k}}\) సదిశలైతే \(2 \bar{a}+\bar{b}, \bar{a}+2 \bar{b}\) సదిశల మధ్య కోణాన్ని కనుక్కోండి.
Solution:
ఇక్కడ \(\bar{a}=2 \bar{i}+2 \bar{j}-3 \bar{k}\), \(\overline{\mathrm{b}}=3 \overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}\)

II.

Question 1.
XOY-తలానికి సమాంతరంగా ఉంటూ, \(4 \bar{i}-3 \bar{j}+\bar{k}\) సదిశకు లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
Solution:
XOY-తలానికి సమాంతరంగా ఉండే సదిశ \(p \bar{i}+q \bar{j}\) రూపంలో ఉంటుంది.
∴ XOY-తలానికి సమాంతరంగా ఉంటూ \(4 \bar{i}-3 \bar{j}+\bar{k}\) సదిశకు లంబంగా ఉండే సదిశ \(3 \bar{i}+4 \bar{j}\).
\(|3 \bar{i}+4 \bar{j}|=\sqrt{9+16}=5\)
∴ XOY-తలానికి సమాంతరంగా ఉంటూ, \(4 \bar{i}-3 \bar{j}+\bar{k}\) సదిశకు లంబంగా ఉండే యూనిట్ సదిశ = \(\pm \frac{(3 \bar{i}+4 \bar{j})}{5}\)

Question 2.
\(\bar{a}+\bar{b}+\bar{c}=0,|\bar{a}|=3,|\bar{b}|=5,|\bar{c}|=7\) \(\bar{a}, \bar{b}\) ల మధ్య కోణాన్ని కనుక్కోండి.
Solution:

Question 3.
\(\bar{a}, \bar{b}, \bar{c}\) సదిశలు క్రమంగా \(\bar{b}+\bar{c},+\bar{c}+\bar{a}, \bar{a}+\bar{b}\) లకు లంబంగా ఉండి, \(|\bar{a}|=2,|\bar{b}|=3,|\bar{c}|=4\) అయితే, \(\overline{\mathrm{a}}+\overline{\mathrm{b}}+\overline{\mathrm{c}}\) పరిమాణం కనుక్కోండి.
Solution:

Question 4.
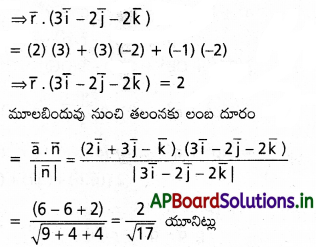
\(\overline{\mathrm{a}}=2 \overline{\mathrm{i}}+3 \overline{\mathrm{i}}-\overline{\mathrm{k}}\) బిందువు గుండా పోతూ \(3 \bar{i}-2 \bar{i}-2 \bar{k}\) సదిశకు లంబంగా ఉండే తలం సమీకరణాన్ని, మూలబిందువు నుంచి ఈ తలానికి గల దూరాన్ని కనుక్కోండి.
Solution:

Question 5.
నాలుగు సతలీయ బిందువుల స్థాన సదిశలు \(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}, \overline{\mathrm{d}}\) లు \((\bar{a}-\bar{b}) \cdot(\bar{b}-\bar{c})=(\bar{b}-\bar{d}) \cdot(\bar{c}-\bar{a})=0\) సమీకరణాలను ధ్రువపరిస్తే, \(\overline{\mathrm{d}}\) బిందువు \(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు శీర్షాలుగా గల త్రిభుజ లంబ కేంద్రం అవుతుందని చూపండి.
Solution:
A, B, C, D బిందువుల స్థాన సదిశలు \(\bar{a}, \bar{b}, \bar{c}, \bar{d}\) లు

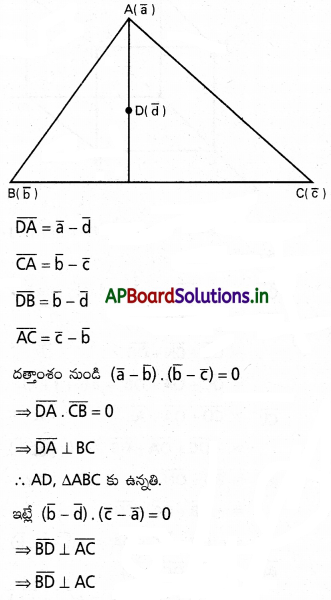
∴ BD, ∆ABC కు ఉన్నతి.
ఉన్నతులు AD, BD లు D వద్ద ఖండించుకుంటాయి.
∴ D, ∆ABC కు లంబ కేంద్రం.

III.

Question 1.
(5, -1, 1), (7, -4, 7), (1, -6, 10), (-1, -3, 4) బిందువులు, ఒక సమ చతురస్రం (rhombus) శీర్షాలవుతాయని చూపండి. [Mar. ’13]
Solution:
A(5, -1, 1), B(7, -4, 7), C(1, -6, 10), D(-1, -3, 4) దత్త బిందువులు.

∵ AB = BC = CD = DA = 7 యూనిట్లు
AC ≠ BD
∴ A, B, C, D బిందువులు సమచతురస్ర శీర్షాలు.

Question 2.
\(\overline{\mathbf{a}}=\mathbf{4} \overline{\mathbf{i}}+5 \overline{\mathbf{j}}-\overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}-4 \overline{\mathbf{j}}+5 \overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=\mathbf{3} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\) మూడు సదిశలు \(\overline{\mathbf{a}}, \overline{\mathbf{b}}\) లు రెండింటికీ లంబంగా ఉంటూ \(\overline{\mathbf{c}}\) పరిమాణానికి 21 రెట్లు పరిమాణం గల సదిశను కనుక్కోండి.
Solution:

Question 3.
ΔABC లో BC, CA, AB ల పొడవులు వరుసగా a, b, c అయి, ఆ త్రిభుజ కేంద్రభాసం G అయితే ‘O’ ఏదైనా బిందువు అయినప్పుడు) a² + b² + c² = 3(OA² + OB² + OC²) – 9(OG)² అని చూపండి.
Solution:

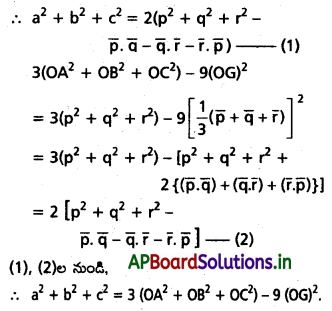
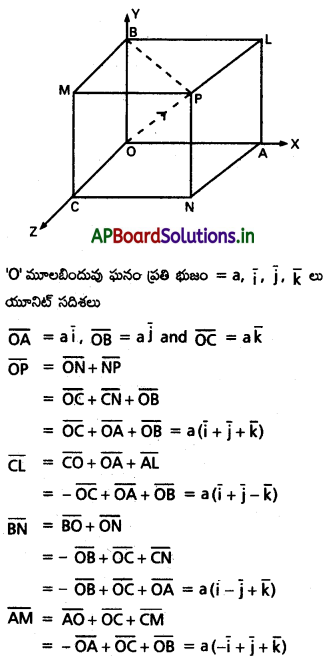
Question 4.
ఘనం కర్ణాలతో ఒక రేఖ చేసే కోణాలు θ₁, θ₂, θ₃, θ₄ అయితే \(\cos ^2 \theta_1+\cos ^2 \theta_2+\cos ^2 \theta_3+\cos ^2 \theta_4\) = \(\frac{4}{3}\) అవుతుందని చూపండి.
Solution: