AP Inter 1st Year Maths 1A Important Questions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు

సాధించిన సమస్యలు
(Solved Problems)

ప్రశ్న 1.
కింది విలువలు కనుక్కోండి.
(i) sin \(\frac{5 \pi}{3}\)
(ii) tan (855°)
(iii) sec \(\left(\frac{13 \pi}{3}\right)\)
సాధన:
(i) sin \(\frac{5 \pi}{3}\) = sin (2π – \(\frac{\pi}{3}\))
= -sin\(\frac{\pi}{3}\)
= –\(\frac{\sqrt{3}}{2}\)

(ii) tan (855°) = tan (2 × 360° + 135°)
= tan (135°)
= tan (180° – 45°)
= -tan 45° = -1

(iii) sec \(\left(\frac{13 \pi}{3}\right)\)
= sec (4л + \(\frac{\pi}{3}\))
= sec \(\frac{\pi}{3}\)
= 2

ప్రశ్న 2.
కింది వాటిని సూక్ష్మీకరించండి.
i) cot \(\left(\theta-\frac{13 \pi}{2}\right)\)
సాధన:

ii) tan \(\left(-23 \frac{\pi}{3}\right)\)
సాధన:

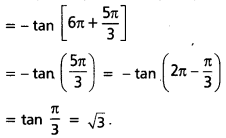
ప్రశ్న 3.
sin² \(\frac{\pi}{10}\) + sin² \(4\frac{\pi}{10}\) + sin² \(\frac{6\pi}{10}\) + sin² \(\frac{9\pi}{10}\) విలువను కనుక్కోండి.
సాధన:

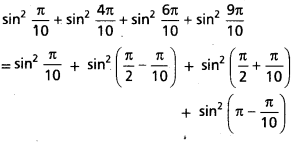
= sin² \(\frac{\pi}{10}\) + cos² \(\frac{\pi}{10}\) + cos² \(\frac{\pi}{10}\) + sin² \(\frac{\pi}{10}\)
= 2 (∵ sin² θ + cos² θ = 1 ∀ θ)

ప్రశ్న 4.
sin θ = \(\frac{4}{5}\), θ మొదటి పాదంలో లేకపోతే cos θ విలువను కనుక్కోండి.
సాధన:
∵ sin θ = \(\frac{4}{5}\), θ మొదటి పాదంలో లేదు.
⇒ θ, రెండవ పాదంలో ఉంటుంది. . sin θ +ve కనుక,
⇒ cos θ = – \(\sqrt{1-\sin ^2 \theta}\) = –\(\sqrt{1-\left(\frac{4}{5}\right)^2}=\frac{-3}{5}\)
cos θ = –\(\frac{3}{5}\)

ప్రశ్న 5.
sec θ + tan θ = \(\frac{2}{3}\) అయితే, sin θ విలువ కనుక్కొని, θ ఏ పాదంలో ఉంటుందో కనుక్కోండి.
సాధన:
∵ sec θ + tan θ = \(\frac{2}{3}\)
⇒ sec θ – tan θ = \(\frac{3}{2}\) ; (∵ sec² θ – tan² θ = 1)
⇒ 2 sec θ = \(\frac{2}{3}\) + \(\frac{3}{2}\) = \(\frac{4+9}{6}\) = \(\frac{13}{6}\)
∴ sec θ = \(\frac{13}{12}\)
ఇంకా 2 tan θ = \(\frac{2}{3}\) – \(\frac{3}{2}\) = \(\frac{4-9}{6}\) = \(\frac{-5}{6}\)
∴ tan θ = \(\frac{-5}{12}\)
ఇప్పుడు sin θ = \(\frac{\tan \theta}{\sec \theta}=\frac{\left(\frac{-5}{12}\right)}{\left(\frac{13}{12}\right)}=\frac{-5}{13}\)
∵ tan θ రుణాత్మకం, sec θ ధనాత్మకం.
⇒ θ నాలుగో పాదంలో ఉంటుంది.

ప్రశ్న 6.
cot \(\frac{\pi}{16}\) . cot \(\frac{2\pi}{16}\) . cot \(\frac{3\pi}{16}\) …………. cot \(\frac{7\pi}{16}\) = 1 అని నిరూపించండి.
సాధన:
L.H.S. = \(\frac{\pi}{16}\) . cot \(\frac{2\pi}{16}\) . cot \(\frac{3\pi}{16}\) …………. cot \(\frac{7\pi}{16}\)
= \(\left(\cot \frac{\pi}{16} \cdot \cot \frac{7 \pi}{16}\right)\left(\cot \frac{2 \pi}{16} \cdot \cot \frac{6 \pi}{16}\right)\) \(\left(\cot \frac{3 \pi}{16}, \cot \frac{5 \pi}{16}\right) \cot \left(\frac{4 \pi}{16}\right)\)

= (1) (1) (1) (1) = 1

ప్రశ్న 7.
3 sin θ + 4 cos θ = 5 అయితే 4 sin θ – 3 cos θ విలువ కనుక్కోండి.
సాధన:
3 sin θ + 4 cos θ = 5
4 sin θ – 3 cos θ = x అనుకుందాం
పై సమీకరణాలను వర్గం చేసి, కలిపితే
(3 sin θ + 4 cos θ)² + (4 sin θ – 3 cos θ)² = 5² + x²
⇒ 9 sin² + 16 cos² θ + 24 sin θ cos θ + 16 sin² θ + 9 cos² θ – 24 sin θ cos θ = 25 + x²
⇒ 9 + 16 = 25 + x²
⇒ x² = 0 ⇒ x = 0
∴ 4 sin θ – 3 cos θ = 0

ప్రశ్న 8.
cos θ + sin θ = \(\sqrt{2}\) cos θ అయితే cos θ – sin θ = \(\sqrt{2}\) sin θ అని చూపండి. [May ’11]
సాధన:
cos θ + sin θ = \(\sqrt{2}\) cos θ
sin θ = (\(\sqrt{2}\)-1) cos θ
ఇరువైపులా ( \(\sqrt{2}\) + 1) తో గుణిస్తే
⇒ (\(\sqrt{2}\) + 1) sin θ = (\(\sqrt{2}\) + 1) ( \(\sqrt{2}\) – 1) cos θ
⇒ (\(\sqrt{2}\) + 1) sin θ = (2 – 1) cos θ
⇒ \(\sqrt{2}\) sin θ + sin θ = cos θ
∴ cos θ – sin θ = \(\sqrt{2}\) sin θ

ప్రశ్న 9.
2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ) విలువను కనుక్కోండి,
సాధన:
2(sin⁶ θ + cos⁶ θ) – 3(sin⁴ θ + cos⁴ θ)
= 2[(sin² θ)³ + (cos² θ)³] – 3[(sin² θ)² + (cos² θ)²]
= 2[(sin² θ+ cos² θ)3 – 3 sin² θ cos² θ (sin² θ + cos² θ)] – 3[(sin²θ+ cos² θ)2 – 2 sin² θ cos² θ]
= 2[1 – 3 sin² θ cos² θ] – 3[1 – 2 sin² θ cos² θ]
= 2 – 6 sin² θ cos² θ – 3 + 6 sin² θ cos² θ
= -1

ప్రశ్న 10.
(tan θ + cot θ)² = sec² θ + cosec² θ = sec² θ. cosec² θ అని నిరూపించండి.
సాధన:
(tan θ + cot θ)²
= tan²θ+ cot² θ + 2 tan θ cot θ
= tan²θ + cot²θ + 2
= (1 + tan²θ) + (1 + cot² θ)
= sec² θ + cosec² θ
ఇంకా sec² θ. cosec² = \(\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin ^2 \theta \cdot \cos ^2 \theta}\)
= \(\frac{1}{\cos ^2 \theta} \cdot \frac{1}{\sin ^2 \theta}\)
sec² θ. cosec²

ప్రశ్న 11.
cos θ > 0, tan θ + sin θ = m, tan θ – sin θ = n అయితే m² – n² = 4\(\sqrt{mn}\) అని చూపండి.
సాధన:
m = tan θ + sin θ
n = tan θ – sin θ
⇒ m + n = 2 tan θ
m – n = 2 sin θ
(m + n) (m – n) = 4 tan θ sin θ
⇒ m² – n² = 4\(\sqrt{\tan ^2 \theta \cdot \sin ^2 \theta}\)
= 4\(\sqrt{\tan ^2 \theta\left(1-\cos ^2 \theta\right)}\)
= 4\(\sqrt{\tan ^2 \theta-\sin ^2 \theta}\)
= 4\(\sqrt{(\tan \theta+\sin \theta)(\tan \theta-\sin \theta)}\)
= 4\(\sqrt{m n}\)
∴ m² – n² = 4\(\sqrt{m n}\)

ప్రశ్న 12.
tan 20° = λ అయితే , \(\frac{\tan 160^{\circ}-\tan 110^{\circ}}{1+\tan 160^{\circ} \cdot \tan 110^{\circ}}\) = \(\frac{1-\lambda^2}{2 \lambda}\) అని నిరూపించండి.
సాధన:
tan 20° = λ

ప్రశ్న 13.
sin 75°, cos 75°, tan 75°, cot 75° యొక్క విలువలను కనుక్కోండి.
సాధన:
i) sin 75° = sin (45° + 30°)
sin 45°. cos 30° + cos 45°. sin 30°
= \(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)\)
= \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\)

ii) cos (75°) = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°
= \(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)\)
= \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

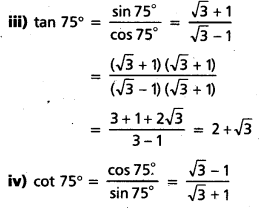
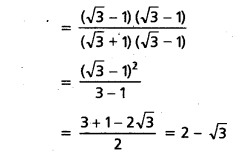
ప్రశ్న 14.
cos A = \(\frac{5}{13}\), sin B = \(\frac{4}{5}\) 0 < A, B < 90° అయితే sin (A + B) విలువ కనుక్కోండి.
సాధన:
0 < A < 90°, cos A = \(\frac{5}{13}\) ⇒ sin A = \(\frac{12}{13}\)
0 < B < 90°, sin B = \(\frac{4}{5}\) ⇒ cos B = \(\frac{3}{5}\)
∴ sin (A + B) = sin A cos B + cos A sin B
= \(\frac{12}{13}\) . \(\frac{3}{5}\) + \(\frac{5}{13}\) . \(\frac{4}{5}\)
= \(\frac{56}{65}\)

ప్రశ్న 15.
sin²\(\left(52 \frac{1}{2}\right)^{\circ}\) – sin²\(\left(22 \frac{1}{2}\right)^{\circ}\) = \(\frac{\sqrt{3}+1}{4 \sqrt{2}}\) అని నిరూపించండి.
సాధన:
సూచన : sin² A – sin² B = sin (A + B). sin (A – B)
∴ sin² 52\(\frac{1}{2}\) – sin² 22\(\frac{1}{2}\)
= sin (52\(\frac{1}{2}\)° +22\(\frac{1}{2}\)°) . sin (52\(\frac{1}{2}\)° – 22\(\frac{1}{2}\)°)
= sin (75°). sin 30°
= \(\frac{1}{2}\) sin (45° + 30°)
= \(\frac{1}{2}\) [sin 45° cos 30° + cos 45° sin 30°]
= \(\frac{1}{2}\left[\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)+\frac{1}{\sqrt{2}} \cdot \frac{1}{2}\right]\)
= \(\frac{\sqrt{3}+1}{4 \sqrt{2}}\)

ప్రశ్న 16.
tan 70° – tan 20° = 2 tan 50° అని నిరూపించండి.
సాధన:
tan 50° = tan (70° – 20°)
= \(\frac{\tan 70^{\circ}-\tan 20^{\circ}}{1+\tan 20^{\circ} \tan 70^{\circ}}\)
⇒ tan 70° – tan 20°
= tan 50° [1 + tan 20° tan (90° – 20°)]
⇒ tan 70° – tan 20° = tan 50° [1 + tan 20° cot 20°]
⇒ tan 70° – tan 20° = 2 tan 50°

ప్రశ్న 17.
A + B = π/4 అయితే ,
i) (1 + tan A) (1 + tan B) = 2, [Mar. 11, ’07]
ii) (cot A – 1) (cot B – 1) = 2 అని నిరూపించండి.
సాధన:
i) A + B = π/4
⇒ tan (A + B) = tan (π/4)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = 1
⇒ tan A + tan B = 1 – tan A tan B
⇒ tan A + tan B + tan A tan B = 1
ఇరువైపులా ‘1’ కలుపగా
⇒ 1 + tan A + tan B + tan A tan B = 1 + 1
⇒ (1 + tan A) (1 + tan B) = 2

ii) A + B = π/4
⇒ cot (A + B) = cot π/4
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}\) = 1
⇒ cot A cot B – 1 = cot B + cot A
⇒ cot A cot B – cot A – cot B = 1
ఇరువైపులా ‘1’ కలుపగా
cot A cot B – cot A – cot B + 1 = 1 + 1
∴ (cot A – 1) (cot B – 1) = 2.

ప్రశ్న 18.
sin α = \(\frac{1}{\sqrt{10}}\), sin β = \(\frac{1}{\sqrt{5}}\), α, β లము కోణాలయితే α + β = π/4 అని చూపండి.
సాధన:
α ఒక లఘు కోణం, sin α = \(\frac{1}{\sqrt{10}}\) ⇒ tan α = \(\frac{1}{2}\)
β ఒక లఘు కోణం, sin β = \(\frac{1}{\sqrt{5}}\) ⇒ tan β = \(\frac{1}{2}\)
కనుక tan (α + β) = \(\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\)
= \(\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{3} \cdot \frac{1}{2}}\) = 1 ⇒ α + β = π/4

ప్రశ్న 19.
sin A = \(\frac{12}{13}\), cos B = \(\frac{3}{5}\), A, B రెండూ మొదటి పాదంలో లేకపోతే, A + B ఏ పాదంలో ఉందో కనుక్కోండి.
సాధన:
sin A = \(\frac{12}{13}\), A మొదటి పాదంలో లేదు.
⇒ A రెండవ పాదంలో ఉంటుంది ∵ sin A +ve
cos B = \(\frac{3}{5}\), θ మొదటి పాదంలో లేదు.
⇒ B నాల్గవ పాదంలో ఉంటుంది ∵ cos B +ve
∵ sin A = \(\frac{12}{13}\) ⇒ cos A = \(\frac{-5}{13}\)
cos B = \(\frac{3}{5}\) ⇒ sin B = \(\frac{-4}{5}\)
sin (A+B) sin A cos B + cos A sin B
= \(\left(\frac{12}{13}\right)\left(\frac{3}{5}\right)+\left(\frac{-5}{13}\right)\left(\frac{-4}{5}\right)\)
= \(\frac{36+20}{65}\) = \(\frac{56}{65}\)
cos (A+B)= cos A cos B – sin A sin B.
= \(\left(\frac{-5}{13}\right)\left(\frac{3}{5}\right)-\left(\frac{12}{13}\right)\left(\frac{-4}{5}\right)\)
= \(\frac{-15+48}{65}\) = \(\frac{33}{65}\)
∵ sin (A + B), cos (A + B) లు రెండూ ధనాత్మకాలు
⇒ (A + B) మొదటి పాదంలో ఉంటుంది.

ప్రశ్న 20.
(i) tan A పదాలలో tan \(\left(\frac{\pi}{4}+\mathrm{A}\right)\) ని,
(ii) cot A పదాలలో cot \(\left(\frac{\pi}{4}+\mathrm{A}\right)\) ని కనుక్కోండి.
సాధన:

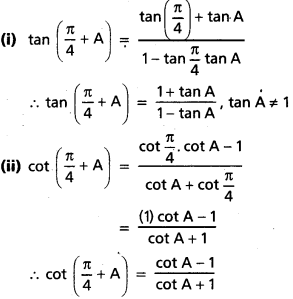
ప్రశ్న 21.
\(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}\) = cot 36° అని నిరూపించండి. [(A.P) Mar. 15, ’11
సాధన:
L.H.S. = \(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}\)
లవ, హారాలను cos 9° తో భాగిస్తే,
= \(\frac{1+\tan 9^{\circ}}{1-\tan 9^{\circ}}\) [∵ tan \(\left(\frac{\pi}{4}+\theta\right)=\frac{1+\tan \theta}{1-\tan \theta}\)]
= tan (45° + 9°)
= tan (54°)
= tan (90° – 36°) = cot 36°
∴ \(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}\) = cot 36°.

ప్రశ్న 22.
cos 42° + cos 78° + cos 162° 0 అని చూపండి. [May ’11]
సాధన:
L.H.S.= cos 42° + cos 78° + cos 162°
= 2 cos \(\left(\frac{42^{\circ}+78^{\circ}}{2}\right)\) . cos \(\left(\frac{42^{\circ}-78^{\circ}}{2}\right)\) + cos (180° – 18°)
= 2 cos 60°. cos (-18°) + cos (180° – 18°)
= 2\(\left(\frac{1}{2}\right)\) cos 18° – cos 18° = 0
∴ cos 42° + cos 78° + cos 162°
= 0

ప్రశ్న 23.
\(\sqrt{3}\) sin θ + cos θ ని ఒక కోణానికి sine. గా వ్యక్తపరచండి.
సాధన:
\(\sqrt{3}\) sin θ + cos θ = 2(\(\frac{\sqrt{3}}{2}\) sinθ + \(\frac{1}{2}\)cos θ)
= 2(cos \(\frac{\pi}{6}\) sin 0 + sin \(\frac{\pi}{6}\) cos θ)
= 2. sin (θ + \(\frac{\pi}{6}\)).

ప్రశ్న 24.
sin² θ + sin² [θ – \(\frac{\pi}{3}\)] + sin² [θ – \(\frac{\pi}{3}\)] = \(\frac{3}{2}\) అని చూపండి.
సాధన:
LHS = sin² θ + sin² [θ – \(\frac{\pi}{3}\)] + sin² [θ – \(\frac{\pi}{3}\)]
= sin² θ + (sin θ cos \(\frac{\pi}{3}\) + cos θ sin \(\frac{\pi}{3}\))² + (sin θ cos cos \(\frac{\pi}{3}\) – cos \(\frac{\pi}{3}\) sin θ)²
= sin² θ + 2 (sin² θ cos² \(\frac{\pi}{3}\) + cos² θ sin²\(\frac{\pi}{3}\))
= sin² θ + 2 (sin² θ . \(\frac{1}{4}\) + cos²θ . \(\frac{3}{4}\))
= sin² θ + \(\frac{1}{2}\) sin² θ + \(\frac{3}{2}\) cos² θ
= \(\frac{3}{2}\) sin² θ + \(\frac{3}{2}\) cos² θ = \(\frac{3}{2}\) (sin² θ + cos² θ)
= \(\frac{3}{2}\) = R.H.S.

ప్రశ్న 25.
A, B, C లు ఒక త్రిభుజంలోని కోణాలు అవుతూ, వీటిలో ఏ ఒక్కటీ \(\frac{\pi}{2}\) కానప్పుడు
i) tan A+ tan B + tan C = tan A tan B tan C
ii) cot A cot B+ cot B cot C + cot C cot A = 1 అని నిరూపించండి.
సాధన:
i) A, B, C లు త్రిభుజ కోణాలు.
⇒ A + B + C = 180°
⇒ A + B = 180° – C
⇒ tan (A + B) = tan (180° – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = -tan C
⇒ tan A + tan B = -tan C + tan A tan B tan C
⇒ tan A + tan B + tan C = tan A tan B tan C

ii) A + B + C = 180°
⇒ A+B 180° – C
⇒ cot (A + B) = cot (180° – C)
⇒ \(\frac{\cot A \cot B-1}{\cot B+\cot A}\) = -cot C
⇒ cot A cot B – 1 = -cot B cot C – cot C. cot A
⇒ cot A cot B + cot B cot C + cot C cot A = 1

ప్రశ్న 26.
ABC త్రిభుజంలో cot A + cot B + cot C = \(\sqrt{3}\) అయితే, ABC ఒక సమబాహు త్రిభుజమని చూపండి.
సాధన:
A + B + C = 180°
పై లెక్క నుండి
cot A cot B + cot B cot C+ cot C cot A = 1
i.e., Σ (cot A cot B) = 1 ………………. (1)
ఇప్పుడు (cot A – cot B)²
= Σ (cot² A + cot² B – 2 cot A cot B)
= 2 cot² A + 2 cot² B + 2 cot² C – 2 cot A cot B – 2 cot B cot C – 2 cot C cot A
= 2 [cot A+ cot B + cot C]² – 6 (cot A cot B + cot B cot C + cot C cot A)
= 2|(\(\sqrt{3}\))2 | – 6(1)
= 6 – 6 = 0
∴ Σ (cot A – cot B)² = 0
⇒ cot A = cot B = cot C
⇒ cot A = cot B = cot C = \(\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}\)
(∵ cot A + cot B + cot C = \(\sqrt{3}\))
⇒ A = B = C = 60°
∴ ∆ABC సమబాహు త్రిభుజం

ప్రశ్న 27.
x = tan A, y tan B, z = tan C, A, B, C, A – B, B – C, C – A లలో ఏ ఒక్కటి కూడ \(\frac{\pi}{2}\) బేసి గుణిజం కానట్లయితే \(\Sigma\left(\frac{x-y}{1+x y}\right)=\pi\left(\frac{x-y}{1+x y}\right)\) అని చూపండి.
సాధన:
∵ x = tan A, y = tan B, z = tan C
అప్పుడు. \(\frac{x-y}{1+x y}=\frac{\tan A-\tan B}{1+\tan A \tan B}\) = tan (A – B)
ఇదే విధంగా \(\frac{y-z}{1+y z}\) = tan (B – C) మరియు
\(\frac{z-x}{1+z x}\) = tan (C – A)
P = A – B, Q = B – C, R = C – A అని రాస్తే
P + Q + R = 0 కనుక
⇒ P + Q = R
⇒ tan (P + Q) = tan (-R)
⇒ \(\frac{\tan P+\tan Q}{1-\tan P \tan Q}\) = -tan R
⇒ tan P + tan Q = -tan R + tan P tan Q tan R
⇒ tan P + tan Q + tan R = tan P tan Q tan R
⇒ Σ (tan P) = π (tan P)
⇒Σ tan (A – B) = π tan (A – B)
∴ \(\Sigma\left(\frac{x-y}{1+x y}\right)=\pi\left(\frac{x-y}{1+x y}\right)\)

ప్రశ్న 28.
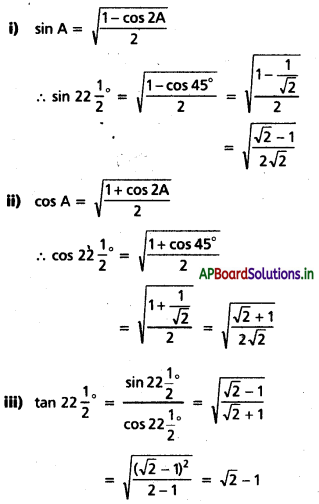
i) sin 22\(\frac{1}{2}\)°
ii) cos 22\(\frac{1}{2}\)°
iii) tan 22\(\frac{1}{2}\)°
iv) cot 22\(\frac{1}{2}\)° విలువలను కనుక్కోండి.
సాధన:
A = 2222\(\frac{1}{2}\)° అయిన 2A = 45° అవుతుంది.

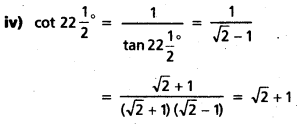
ప్రశ్న 29.
కింది విలువలను కనుక్కోండి.
i) sin 67\(\frac{1}{2}\)°
ii) cos 67\(\frac{1}{2}\)°
iii) tan 67\(\frac{1}{2}\)°
iv) cot 67\(\frac{1}{2}\)°
సాధన:
A = 67\(\frac{1}{2}\)° అయిన 2A = 135° అవుతుంది.

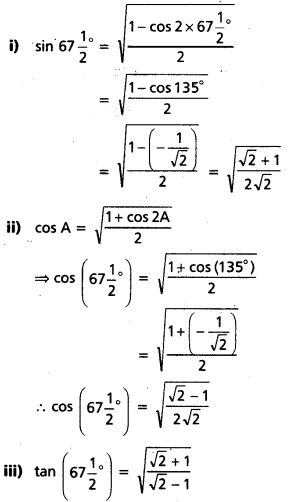
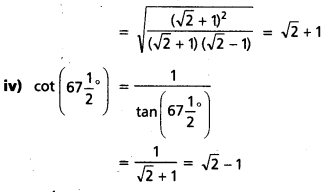
ప్రశ్న 30.
\(\frac{1-\cos 2 \theta}{\sin 2 \theta}\) సూక్ష్మీకరించండి.
సాధన:
\(\frac{1-\cos 2 \theta}{\sin 2 \theta}=\frac{2 \sin ^2 \theta}{2 \sin \theta \cos \theta}=\frac{\sin \theta}{\cos \theta}\) = tan θ.

ప్రశ్న 31.
cos A = \(\sqrt{\frac{\sqrt{2}+1}{2 \sqrt{2}}}\) అయితే cos 2A విలువను కనుక్కోండి.
సాధన:
cos 2A = 2cos² A – 1 = 2 \(\left(\frac{\sqrt{2}+1}{2 \sqrt{2}}\right)\) – 1
= \(\sqrt{\frac{\sqrt{2}+1}{2 \sqrt{2}}}\) – 1
= \(\frac{1}{\sqrt{2}}\)

ప్రశ్న 32.
\(\frac{\pi}{2}\) < 0 < π, cos θ = \(\frac{-5}{13}\) అయితే sin 2θ విలువను కనుక్కోండి.
సాధన:
\(\frac{\pi}{2}\) < θ < π ⇒ sin θ > 0, cos θ = –\(\frac{5}{13}\)
⇒ sin θ = \(\frac{12}{13}\)
∴ sin 2θ = 2 sin θ.cos θ
= 2 . \(\frac{12}{13}\left(\frac{-5}{13}\right)\) = \(\frac{-120}{169}\)

ప్రశ్న 33.
ప్రథమ పాదంలోని x యొక్క ఏ విలువలకు \(\frac{2 \tan x}{1-\tan ^2 x}\) ధనాత్మకం.
సాధన:
\(\frac{2 \tan x}{1-\tan ^2 x}\) > 0 ⇒ tan 2x > 0
⇒ 0 < 2x < \(\frac{\pi}{2}\) (x మొదటి పాదంలోని కోణం కనక)
⇒0 < x < \(\frac{\pi}{4}\)

ప్రశ్న 34.
π < θ < \(\frac{3\pi}{2}\), cos θ = \(\frac{-3}{5}\) అయితే tan θ/2 విలువను కనుక్కోండి.
సాధన:
tan \(\frac{\theta}{2}=\pm \sqrt{\frac{1-\cos \theta}{1+\cos \theta}}=\pm \sqrt{\frac{1+\frac{3}{5}}{1-\frac{3}{5}}}\) = ±2
దత్తాంశం నుంచి π < θ < \(\frac{3\pi}{2}\) ⇒ \(\frac{\pi}{2}\) < \(\frac{\theta}{2}\) < \(\frac{3\pi}{4}\)
⇒ tan θ/2 < 0
∴ tan θ/2 = -2

ప్రశ్న 35.
A అనేది \(\frac{\pi}{2}\) పూర్ణాంక గుణిజం కాకపోతే
i) tan A + cot A = 2 cosec 2A
ii) cot A tan A = 2 cot 2A
సాధన:
i) tan A + cot A = \(\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}\)

∴ tan A + cot A = 2 cosec 2A

ప్రశ్న 36.
θ అనేది \(\frac{\pi}{2}\) పూర్ణాంక గుణిజం కాకపోతే, tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = cot θ అని నిరూపించండి.
సాధన:
cot A – tan A = 2 cot 2A
tan A = cot A – 2 cot 2A అని వస్తుంది ……………… (1)
కనుక , tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ
= (cot θ – 2 cot 2θ) + 2 (cot 2θ – 2 cot 4θ) + 4 (cot 4θ – 2 cot 8θ) + 8 cot 8θ
(సమీకరణం (1) నుంచి)
cot θ

ప్రశ్న 37.
A ∈ R అయితే,
i) sin A sin (π/3 + A) sin (π/3 – A) = \(\frac{1}{4}\) sin 3A
ii) cos A. cos (π/3 + A) cos (π/3 – A) = \(\frac{1}{4}\) cos 3A అని నిరూపించి తద్వారా
iii) sin 20° sin 40° sin 60° sin 80° = \(\frac{3}{16}\)
iv) cos \(\frac{\pi}{9}\) cos \(\frac{2\pi}{9}\) cos \(\frac{3\pi}{9}\) cos \(\frac{4\pi}{9}\) = \(\frac{1}{16}\) అని రాబట్టండి.
సాధన:
i) sin A. sin (π/3 + A). sin (π/3 – A)
sin A [sin² π/3 sin² A]
= [sin (A + B). sin (A – B)
= sin² A – sin² B = cos² B – cos² A]
= sin A \(\left[\left(\frac{3}{2}\right)-\sin ^2 \mathrm{~A}\right]\)
= sin A \(\left(\frac{3-4 \sin ^2 A}{4}\right)\)
= \(\frac{1}{4}\) (3 sin A – 4 sin³ A)
= \(\frac{1}{4}\) |sin 3A|

ii) cos A cos (π/3 + A) cos (π/3 – A)
= cos A (cos² A – sin² \(\frac{\pi}{3}\)_
= cos A (cos² A – \(\frac{3}{4}\))
= \(\frac{\cos A\left(4 \cos ^2 A-3\right)}{4}\)
= \(\frac{1}{4}\) (4 cos³ A – 3 cos A)
= \(\frac{1}{4}\) . cos 3A
= \(\frac{1}{4}\) [4 cos³ A – 3 cos A]
= \(\frac{1}{4}\) cos 3A

iii) (1) A 20° ప్రతిక్షేపిస్తే,
⇒ sin 20°. sin (60° + 20°) sin (60° – 20°) = \(\frac{1}{4}\) sin 3(20°)
లేదా sin 20° sin 80° sin 40° = \(\frac{1}{4}\) sin 60°
పై సమీకరణాన్ని ఇరువైపులా sin 60° తో గుణిస్తే
sin 20° sin 40° sin 60° sin 80°
= \(\frac{1}{4}\) sin² 60° = \(\frac{1}{4}\) \(\frac{3}{4}\) = \(\frac{3}{16}\)
ఇదేవిధంగా, (ii) నుంచి

iv) cos 20° cos 40° cos 80° = \(\frac{1}{4}\) . cos 60° అని వస్తుంది.
ఇరువైపులా cos 60° తో గుణిస్తే
cos 20° cos 40° cos 60° cos 80°
= \(\frac{1}{4}\) cos² 60° = \(\frac{1}{16}\)
అంటే cos \(\frac{\pi}{9}\) cos \(\frac{2\pi}{9}\) cos \(\frac{3\pi}{9}\) cos \(\frac{4\pi}{9}\) = \(\frac{1}{16}\)

ప్రశ్న 38.
3A అనేది \(\frac{\pi}{2}\) కి బేసి గుణిజం కాకపోతే, tan A. tan(60° + A). tan (60° – A) = tan 3A అని నిరూపించి తర్వాత tan 6° tan 42° tan 66° tan 78° విలువను కనుక్కోండి.
సాధన:
sin A sin (π/3 + A) sin (π/3 – A) = 1/4 sin 3A
cos A cos (π/3 + A) cos (π/3 – A) = 1/4 cos 3A
sin A. sin (60° + A). sin (60° – A) = \(\frac{1}{4}\) sin 3A …………… (1)
cos A.cos (60° + A). cos (60° – A) = \(\frac{1}{4}\) cos 3A …………… (2)
(1) ని (2) తో భాగిస్తే
tan A. tan (60° + A). tan (60° – A) = tan 3A …………….. (3)
(3) లో A = 6° ప్రతిక్షేపిస్తే
tan 6°. tan 66°. tan 54° = tan 18° …………… (4)
మళ్ళీ (3) లో A = 18° ప్రతిక్షేపిస్తే
tan 18°. tan 78°. tan 42° = tan 54° …………… (5)
(4), (5) సమీకరణాలను గుణిస్తే
(tan 6°. tan 66°. tan 54°).
(tan 18°. tan 78°. tan 42°) = tan 18°. tan 54°
కనుక tan 6°. tan 42°. tan 66°. tan 78° = 1.

ప్రశ్న 39.
α, β ∈ R అయితే , (cos α + cos β)² + (sin α + sin β)² = 4 cos² \(\frac{(\alpha+\beta)}{2}\) అని నిరూపించండి.
సాధన:
L.H.S. = (cos α + cos β)² + (sin α + sin β)²
= (cos² α + cos² β + 2 cos α cos β) + (sin² α + sin² β + 2 sin α sin β)
= 1 + 1 + 2 (cos α cos β + sin α sin β)
= 2 + 2 cos (α – β)
= 2 [1 + cos (α – β)]
= 2[2 cos² \(\frac{(\alpha+\beta)}{2}\)]
= 4. cos² \(\frac{(\alpha+\beta)}{2}\) [∵ 1+ cos θ = 2 cos² = \(\frac{\theta}{2}\)]

ప్రశ్న 40.
a, b, c లు శూన్యేతర వాస్తవ సంఖ్యలు, a cos θ + b sin θ = c సమీకరణానికి సాధనలు α, β లు అయితే
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\) అని చూపిండి.
సాధన:
∵ a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ (a cos θ)² = (c – b sin θ)²
⇒ a² cos² θ = c² + b² sin² θ – 2bc sin θ
⇒ a² (1 – sin² θ) = c² + b² sin² θ – 2bc sin θ
⇒ (a² + b²) sin² θ – 2bc sin θ + (c² – a²) = 0
ఇది sin θ లో వర్గ సమీకరణం. sin α, sin β లు దీనికి మూలాలు
∴ మూలాలు మొత్తం = sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
మూలాల లబ్దం = sin α sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

ప్రశ్న 41.
θ అనేది \(\frac{\pi}{2}\) బేసి గుణిజం కాదు, cos θ ≠ \(\frac{-1}{2}\) అయినప్పుడు, \(\frac{\sin \theta+\sin 2 \theta}{1+\cos \theta+\cos 2 \theta}\) = tan θ అని నిరూపించండి.
సాధన:

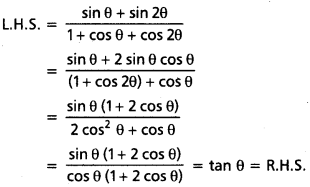
ప్రశ్న 42.
sin⁴ \(\frac{\pi}{8}\) + sin⁴ \(\frac{3\pi}{8}\) + sin⁴ \(\frac{5\pi}{8}\) + sin⁴ \(\frac{7\pi}{8}\) = \(\frac{3}{2}\) అని నిరూపించండి.
సాధన:
L.H.S. = sin⁴ \(\frac{\pi}{8}\) + sin⁴ \(\left(\frac{\pi}{2}-\frac{\pi}{8}\right)\) + sin⁴ \(\left(\frac{\pi}{2}+\frac{\pi}{8}\right)\) + sin⁴ \(\left(\pi-\frac{\pi}{8}\right)\)

ప్రశ్న 43.
2A, 3A లు \(\frac{\pi}{2}\) బేసి గుణిజాలు కానప్పుడు, tan 3A. tan 2A. tan A = tan 3A – tan 2A – tan A అని రుజువు చేయండి.
సాధన:
tan 3A = tan (2A + A)
= \(\frac{\tan 2 A+\tan A}{1-\tan 2 A \tan A}\)
⇒ tan 3A(1 – tan 2A tan A) = tan 2A + tan A
⇒ tan 3A – tan A tan 2A tan 3A = tan 2A + tan A
∴ tan 3A – tan 2A – tan A = tan A tan 2A tan 3A

ప్రశ్న 44.
sin 78° + cos 132° = \(\frac{\sqrt{5}-1}{4}\) అని చూపండి.
సాధన:
L.H.S. = sin 78° + cos 132°
= sin 78° + cos (90° + 42°)
= sin 78° – sin 42°
= 2 cos\(\left(\frac{78^{\circ}+42^{\circ}}{2}\right)\) . sin \(\left(\frac{78^{\circ}-42^{\circ}}{2}\right)\)
= 2 cos (60°), sin (18°)
= 2\(\left(\frac{1}{2}\right)\left(\frac{\sqrt{5}-1}{4}\right)\) = \(\frac{\sqrt{5}-1}{4}\) = R.H.S.

ప్రశ్న 45.
sin 21° cos 9° cos 84° cos 6° = \(\frac{1}{4}\) అని చూపండి.
సాధన:
L.H.S. = sin 21° cos 9° cos 84° cos 6°
= \(\frac{1}{4}\) [2 sin 21° cos 9° 2 cos 84° cos 6°]
= \(\frac{1}{2}\) [sin (21° + 9°) + sin (21° – 9°) – 2 cos (90° – 6°) cos 6°]
= \(\frac{1}{2}\) [sin 30°+ sin 12° – 2 sin 6° cos 6°]
= \(\frac{1}{2}\) [\(\frac{1}{4}\) + sin 12° – sin (2 × 16°)
= \(\frac{1}{4}\) = R.H.S.

ప్రశ్న 46.
sin 34° + cos 64° – cos 4° విలువను కనుక్కోండి .
సాధన:
sin 34° + (cos 64° – cos 4°)
= sin 34° – 2 sin \(\frac{64^{\circ}+4^{\circ}}{2}\) sin \(\frac{64^{\circ}-4^{\circ}}{2}\) [cos C – cosD = – 2 sin \(\left(\frac{C+D}{2}\right)\) sin \(\left(\frac{C-D}{2}\right)\)]
= sin 34° – 2. sin 34°.sin 30°
= 0 (sin 30° = \(\frac{1}{2}\) కనుక)

ప్రశ్న 47.
cos² 76° + cos² 16° – cos 76°. cos 16° = \(\frac{3}{4}\) అని చూపండి.
సాధన:
L.H.S.= cos² 76° + cos² 16° – cos 76° cos 16°
= cos² 76° + (1 – sin² 16°) – \(\frac{1}{2}\) (2 cos 76° cos 16°)
= 1 + (cos² 76° – sin² 16°) – \(\frac{1}{2}\) [cos (76° + 16°) + cos (76° – 16°)]
= 1 + cos (76° +16°). cos (76° -16°) – \(\frac{1}{2}\) [cos 92° + cos 60°]
= 1 + cos (92°). cos 60° – \(\frac{1}{2}\) cos 92° – \(\frac{1}{2}\) cos 60°
= 1 + \(\frac{1}{2}\) . cos 92° – \(\frac{1}{2}\) cos 92° – \(\frac{1}{2}\) × \(\frac{1}{2}\)
= 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
= R.H.S.

ప్రశ్న 48.
a ≠ 0b, sin x + sin y = a, cos x + cos y = b అయితే
i) tan \(\frac{x+y}{2}\)
ii) sin \(\frac{x-y}{2}\) విలువలు a, b లలో కనుక్కోండి.
సాధన:

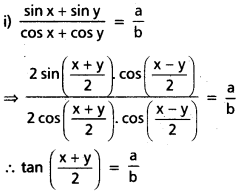
మొదటి పద్ధతి :
ii) a² + b² = (sin x + sin y)² + (cos x + cos y)²
= sin² x + sin² y + 2 sin x sin y + cos² x + cos² y + 2 cos x cos y
= 2 + 2(cos x cos y + sin x sin y)
= 2 + 2 cos(x – y)
= 2[1 + cos(xy)]
a² + b² – 2 = 2 cos(x – y)

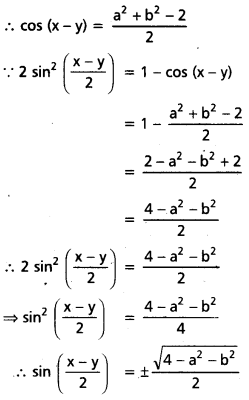
రెండవ పద్ధతి:
a² + b² = (sin x + sin y)² + (cos x + cos y)²

ప్రశ్న 49.
cos 12° + cos 84° + cos 132° + cos 156° = –\(\frac{1}{2}\) అని చూపండి.
సాధన:
L.H.S.= cos 12° + cos 84° + cos 132° + cos 156°
= (cos 132°+ cos 12°) + (cos 156° + cos 84°)
= 2 cos \(\left(\frac{132^{\circ}+12^{\circ}}{2}\right)\) . cos \(\left(\frac{132^{\circ}-12^{\circ}}{2}\right)\) + 2 cos \(\left(\frac{156^{\circ}+84^{\circ}}{2}\right)\) . cos \(\left(\frac{156^{\circ}-84^{\circ}}{2}\right)\)
= 2 cos 72°. cos 60° + 2 cos (120°). cos (36°)
= 2 cos (90° – 18°)\(\left(\frac{1}{2}\right)\) + 2\(\left(\frac{-1}{2}\right)\) cos 36°
= sin 18° – cos 36°
= \(\left(\frac{\sqrt{5}-1}{4}\right)-\left(\frac{\sqrt{5}+1}{4}\right)=\frac{-1}{2}\) = R.H.S

ప్రశ్న 50.
ప్రతీ θ ∈ R కి, 4 sin \(\frac{5 \theta}{2}\) cos \(\frac{2 \theta}{2}\) cos 3θ = sin θ – sin 2θ + sin 4θ + sin 7θ అని చూపండి.
సాధన:
L.H.S. = 4 sin \(\frac{5 \theta}{2}\) cos \(\frac{2 \theta}{2}\) cos 3θ
= 2 [2 sin \(\frac{5 \theta}{2}\) cos \(\frac{3 \theta}{2}\) . cos 3θ
= 2 [sin\(\left(\frac{5 \theta}{2}+\frac{3 \theta}{2}\right)\) + sin \(\left(\frac{5 \theta}{2}-\frac{3 \theta}{2}\right)\)] cos 3θ
= 2[(sin 4θ + sin θ) cos 3θ]
= 2 sin 4θ cos 3θ + 2 sin θ cos 3θ
= sin (4θ + 3θ) + sin (4θ – 3θ) + sin (θ + 3θ) + sin (θ – 3θ)
= sin 7θ + sin θ + sin 4θ – sin 2θ = R.H.S.

ప్రశ్న 51.
A, B, A + B లలో ఏదీ π కి పూర్ణాంక గుణిజం కాకపోతే, \(\frac{1-\cos A+\cos B-\cos (A+B)}{1+\cos A-\cos B-\cos (A+B)}\) = tan \(\frac{A}{2}\) cot \(\frac{A}{2}\) అని చూపండి.
సాధన:
లవం = 1 – cos A + cos B cos (A + B)
= [1 – cos (A + B)] – (cos A – cos B)

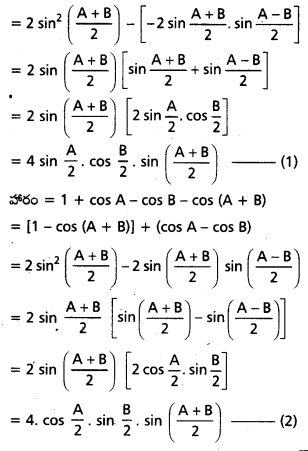
(1), (2) ల నుండి

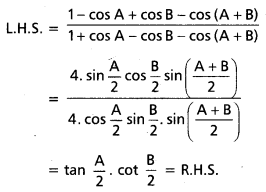
ప్రశ్న 52.
α ∈ R అయితే , cos² (α – π/4) + cos² (α + π/12) – cos² (α – π/12) = \(\frac{1}{2}\) అని చూపండి.
సాధన:
L.H.S. = cos² (α – π/4) + cos² (α + π/12) – cos²(α – π/2)
= \(\frac{1+\cos 2(\alpha-\pi / 2)}{2}\) + {sin (α + π/12 + α – π/12) sin (α – π/12 – α – π/12)}
= \(\frac{1}{2}\) (1 + sin 2α) + sin 2α. sin (π/6)
= \(\frac{1}{2}\)+ \(\frac{1}{2}\) sin 2α – \(\frac{1}{2}\) sin 2α = \(\frac{1}{2}\)
సూచన : cos² A – cos² B = sin (A + B) sin (B – A)

ప్రశ్న 53.
(α – β) అనేది \(\frac{\pi}{2}\) బేసి గుణిజం కాదు, m ≠ – 1, \(\frac{\sin (\alpha+\beta)}{\cos (\alpha-\dot{\beta})}=\frac{1-m}{1+m}\) అయితే tan \(\left(\frac{\pi}{4}-\alpha\right)\) = m. tan \(\left(\frac{\pi}{4}+\beta\right)\) అని చూపండి.
సాధన:


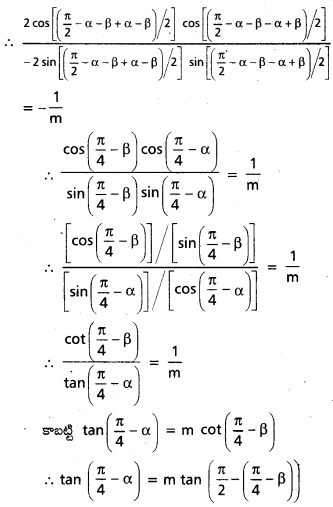
∴ tan \(\left(\frac{\pi}{4}-\alpha\right)\) = m. tan \(\left(\frac{\pi}{4}+\beta\right)\)

ప్రశ్న 54.
A, B, C లు త్రిభుజ కోణాలయితే, కింది వాటిని నిరూపించండి.
i) sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
ii) sin 2A + sin 2B – sin 2C = 4 cos A cos B sin C
సాధన:
i) ∵ A, B, C లు త్రిభుజ కోణాలు
⇒ A + B + C = 180° ……………… (1)
L.H.S. = sin 2A + sin 2B + sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) . cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + sin 2C
= 2 sin (A + B) cos (AB) + sin 2C
= 2 sin (180° C) cos (AB) + sin 2C
(1) నుండి
2 sin C. cos (A – B) + 2 sin C. cos C
= 2 sin C [cos (A – B) + cos C]
= 2 sin C [cos (A – B) + cos (180° – \(\overline{A+B}\))]
= 2 sin C [cos (AB) cos (A + B)] = 2 sin C (2 sin A sin B)
= 4 sin A sin B sin C = R.H.S.

ii) L.H.S. = sin 2A + sin 2B – sin 2C
= 2 sin \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) . cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) – sin 2C
= 2 sin (A + B) cos (A – B) sin 2C
= 2 sin (180° – C) cos (A – B) – sin 2C
= 2 sin C. cos (A – B) – 2 sin C cos C
= 2 sin C [cos (A – B) cos C]
= 2 sin C [cos (A – B) – cos (180° – \(\overline{A+B}\))]
(1) నుండి
= 2 sin C [cos (A – B) + cos (A + B)]
= 2 sin C [2 cos A cos B]
= 4 cos A cos B sin C = R.H.S.

ప్రశ్న 55.
A, B, C లు త్రిభుజ కోణాలైతే, కింది వాటిని నిరూపించండి.
i) cos 2A + cos 2B + cos 2C = -4 cos A cos B cos C – 1
ii) cos 2A + cos 2B – cos 2C = 1 – 4 sin A sin B cos C
సాధన:
i) ∵ A, B, C లు త్రిభుజ కోణాలు.
⇒ A + B + C = 180° ……………. (1)
L.H.S.= (cos 2A + cos 2B) + cos 2C
= 2 cos (A + B) cos (A – B) + 2 cos² C – 1
= -2 cos C cos (A – B) – 2 cos C cos (A + B) – 1
[∵ cos (A + B) = -cos C]
= -1 – 2 cos C [cos (AB) + cos (A – B)]
= -1 – 2 cos C [2 cos A cos B]
= -1 – 4 cos A cos B cos C = R.H.S.

ii) L.H.S.= cos 2A + cos 2B – cos 2C
= 2 cos \(\left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right)\) cos \(\left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) – cos 2C
= 2 cos (A + B). cos (A – B) – (2 cos² C – 1)
= 2 cos (180° – C) cos (A – B) – 2 cos² C + 1
= 1 – 2 cos C cos (A – B) – 2 cos² C
= 1 – 2 cos C [cos (AB) + cos C]
= 1 – 2 cos C [cos (A – B) + cos (180° \(\overline{A+B}\))]
= 1 – 2 cos C [cos (AB) cos (A + B)]
= 1 – 2 cos C [2 sin A sin B]
= 1 – 4 sin A sin B cos C = R.H.S.

ప్రశ్న 56.
A, B, C లు త్రిభుజ కోణాలయితే కింది వాటిని నిరూపించండి.
i) sin A + sin B + sin C = 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\)
ii) cos A + cos B + cos C = 1 + 4 sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) sin \(\frac{C}{2}\)
సాధన:
i) ∵ A, B, C లు త్రిభుజ కోణాలు.
⇒ A + B + C = 180°
L.H.S. = (sin A+ sin B) + sin C

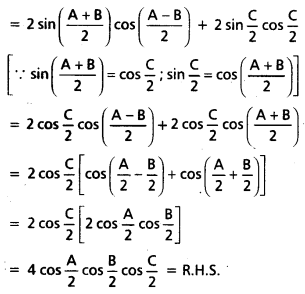
ii) cos A + cos B + cos C = 1 + 4 sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) sin \(\frac{C}{2}\)
L.H.S. = cos A + cos B + cos C

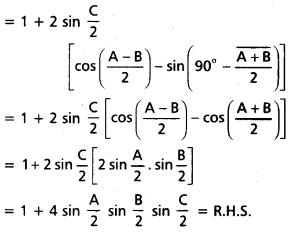
ప్రశ్న 57.
A + B + C = 9 π/2 0° అయితే ,
i) sin² A + sin² B + sin² C = 1 – 2 sin A sin B sin C
ii) sin 2A + sin 2B + sin 2C = 4 cos A cos B cos C అని చూపండి.
సాధన:
i) A + B + C = π/2 ………………. (1)
L.H.S. = sin² A + sin² B + sin² C
= \(\frac{1}{2}\) [1 – cos 2A + 1 – cos 2B + 1 – cos 2C]
= \(\frac{1}{2}\) [3 – (cos 2A + cos 2B + cos 2C)]
= \(\frac{1}{2}\) [3 – (1 + 4 sin A sin B sin C)]
(56(ii)వ లెక్క చూడండి.)
(∵ 2A + 2B + 2C = 180°)
= \(\frac{1}{2}\) [2 – 4 sin A sin B sin C]
= 1 – 2 sin A sin B sin C

ii) A + B + C = π/2
⇒ 2A + 2B + 2C = 180°
sin 2A + sin 2B + sin 2C = 4 cos A cos B cos C
(56(i)వ లెక్క చూడండి.)

ప్రశ్న 58.
A + B + C = 3π/2, cos 2A + cos 2B + cos 2C = 1 – 4 sin A sin B sin C అని చూపండి. [Mar. 13]
సాధన:
A + B + C = 3π/2 …………….. (1)
L.H.S.= cos 2A + cos 2B + cos 2C
= 2 cos (A + B). cos (A – B) + 1 – 2 sin²C
= 2 cos (270° – C). cos (A – B) + 1 – 2 sin²C
= 1 – 2 sin C cos (A – B) – 2 sin² C
= 1 – 2 sin C [cos (A – B) + sin C]
= 1 – 2 sin C [cos (A – B) + sin (270° – \(\overline{A+B}\))]
= 1 – 2 sin C [cos (A – B) – cos (A + B)]
= 1 – 2 sin C [2 sin A sin B]
= 1 – 4 sin A sin B sin C

ప్రశ్న 59.
A, B, C లు త్రిభుజ కోణాలయితే, sin² \(\frac{A}{2}\) + sin² \(\frac{B}{2}\) – sin² \(\frac{C}{2}\) = 1 – 2 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\) అని చూపండి. [May ’11]
సాధన:
A + B + C = 180° …………… (1)

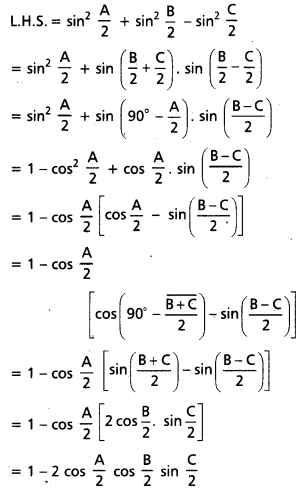
ప్రశ్న 60.
A, B, C లు త్రిభుజ కోణాలయితే sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) + sin\(\frac{C}{2}\) = 1 + 4 sin \(\frac{\pi-A}{4}\) . sin \(\frac{\pi-B}{4}\) sin \(\frac{\pi-C}{4}\) అని రుజువు చేయండి. [Mar. ’14]
సాధన:
A + B + C = 180° …………….. (1)


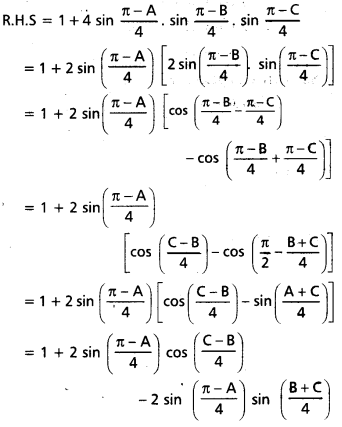
sin\(\frac{A}{2}\) + sin\(\frac{B}{2}\) + sin\(\frac{C}{2}\) = L.H.S

ప్రశ్న 61.
A + B + C = 0 అయితే, cos² A + cosఅయితే B + cosఅయితే C = 1 + 2 cos A cos B cos C అని రుజువు చేయండి.
సాధన:
A + B + C = 0 ………….. (1)
L.H.S. = cos² A + cos² B + cos² C
= cos² A + (1 – sin² B) + cos² C
= 1 + (cos² A – sin² B) + cos² C
= 1 + cos (A + B) cos (A – B) + cos² C
= 1 + cos (-C) cos (A – B) + cos² C
(1) నుండి
= 1 + cos C cos (A – B) + cos² C
= 1 + cos C [cos (A – B) + cos C]
= 1 + cos C [cos (A – B) + cos (- B – A)]
(1) నుండి
= 1 + cos C [cos (A – B) + cos (A + B)]
= 1 + cos C (2 cos A cos B)
= 1 + 2 cos A cos B cos C
= R.H.S.

ప్రశ్న 62.
A + B + C = 2S అయితే cos (S – A) + cos (S – A) + cos (S – B) + cos (S – C) + cos S = 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) cos \(\frac{C}{2}\) అని రుజువు చేయండి.
సాధన:
A + B + C = 2S ……………. (1)
L.H.S. = [cos (S – A) + cos (S – B) + cos (S – C) + cos S]