AP Inter 1st Year Maths 1A Important Questions Chapter 5 సదిశల గుణనం

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 5 సదిశల గుణనం which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 5 సదిశల గుణనం

సాధించిన సమస్యలు
(Solved Problems)

ప్రశ్న 1.
\(\overline{\mathrm{a}}=6 \overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}, \overline{\mathrm{b}}=2 \overline{\mathrm{i}}-9 \overline{\mathrm{j}}+6 \overline{\mathrm{k}}\) అయితే \(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}\) విలువను కనుక్కొని \(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) e కనుక్కోండి.
సాధన:

ప్రశ్న 2.
a = i + 2j – 3k, b = 3i – j + 2k అయితే a + b, a – b సదిశలు పరస్పరం లంబంగా ఉంటాయని చూపండి. [(A.P) Mar. 15; May ’11]
సాధన:

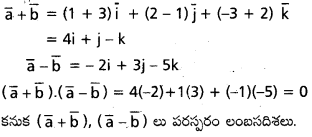
ప్రశ్న 3.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) లు శూన్యేతర, సరేఖీయాలు కాని సదిశలై \(|\overline{\mathrm{a}}+\overline{\mathrm{b}}|=|\overline{\mathrm{a}}-\overline{\mathrm{b}}|\) అయితే \(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) కోణాన్ని కనుక్కోండి.
సాధన:

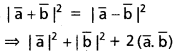
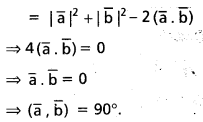
ప్రశ్న 4.
\(|\bar{a}|\) = 11, \(|\bar{b}|\) = 23, \(|\bar{a-b}|\) = 30,అయితే \(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) ల మధ్యకోణాన్ని \(|\overline{\mathrm{a}}+\overline{\mathrm{b}}|\) ను కనుక్కోండి.
సాధన:

ప్రశ్న 5.
\(\overline{\mathrm{a}}=\overline{\mathrm{i}}-\overline{\mathrm{j}}-\overline{\mathrm{k}}, \overline{\mathrm{b}}=2 \overline{\mathrm{i}}-3 \overline{\mathrm{i}}+\overline{\mathrm{k}}\), అయితే \(\overline{\mathrm{a}}\) పై \(\overline{\mathrm{b}}\) యొక్క లంబ విక్షేప సదిశనూ, దాని పరిమాణాన్ని కనుక్కోండి.
సాధన:

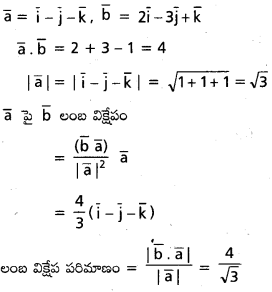
ప్రశ్న 6.
P, Q, R, S బిందువుల స్థాన సదిశలు వరుసగా \(\overline{\mathrm{i}}-\overline{\mathrm{k}},-\overline{\mathrm{i}}+2 \overline{\mathrm{j}}, \mathrm{2 i}-\mathrm{i} \overline{\mathrm{k}}, \mathrm{3} \overline{\mathrm{i}}-\mathrm{2 j}-\overline{\mathrm{k}}\) అయితే \(\overline{\mathrm{P Q}}\) మీద \(\overline{\mathrm{R S}}\) సదిశ యొక్క అంశను కనుక్కోండి.
సాధన:
‘O’ మూలబిందువు.

= \(\frac{(\bar{i}-2 \bar{j}+2 \bar{k}) \cdot(-2 \bar{i}+2 \bar{j}+\bar{k})}{(-2 \bar{i}+2 \bar{j}+\bar{k})}\)
= \(\frac{(-2-4+2)}{\sqrt{4+4+1}}=\frac{-4}{3}\)

ప్రశ్న 7.
\(\lambda \overline{\mathrm{i}}-3 \bar{j}+5 \overline{\mathrm{k}}, 2 \lambda \overline{\mathrm{i}}-\lambda \overline{\mathrm{j}}+\overline{\mathrm{k}}\) సదిశలు పరస్పరం లంబ సదిశలైతే λ ను కనుక్కోండి.
సాధన:
దత్తాంశం ప్రకారం,
⇒ (\(\lambda \overline{\mathrm{i}}-3 \bar{j}+5 \overline{\mathrm{k}}) . (2 \lambda \overline{\mathrm{i}}-\lambda \overline{\mathrm{j}}+\overline{\mathrm{k}}\)) = 0
⇒ λ(2λ) + (-3)(-λ) + 5(-1) = 0
⇒ 2λ² + 3λ – 5 = 0
⇒ (2λ + 5)(λ − 1) = 0
∴ λ = 1 (లేదా) \(\frac{-5}{2}\)

ప్రశ్న 8.
\(\overline{\mathrm{a}}=2 \overline{\mathrm{i}}+3 \overline{\mathrm{j}}+\overline{\mathrm{k}}, \overline{\mathrm{b}}=4 \overline{\mathrm{i}}+\overline{\mathrm{j}}, \quad \overline{\mathrm{c}}=\overline{\mathrm{i}}-\mathrm{3}-7 \overline{\mathrm{k}}\) అనుకొందాం. \(\overline{\mathrm{r}} \cdot \overline{\mathrm{a}}=9, \overline{\mathrm{r}} \cdot \overline{\mathrm{b}}=7, \overline{\mathrm{r}} \cdot \overline{\mathrm{c}}=6\) అయ్యే ఉండే \(\overline{\mathrm{r}}\) సదిశను కనుక్కోండి.
సాధన.
\(\bar{r}=x \bar{i}+y \bar{j}+z \bar{k}\) అనుకొందాం
∴ \(\bar{r} \cdot \bar{a}\) ⇒ 2x + 3y + z = 9
\(\bar{r} \cdot \bar{b}\) = 7 ⇒ 4x + y = = 7
\(\bar{r} \cdot \bar{c}\)= 6 ⇒ x – 3y – 7z = 6
సాధించగా
x = 1, y = 3, z = −2
∴ \(\bar{r}=\bar{i}+3 j-2 k\)

ప్రశ్న 9.
\(2 \overline{\mathrm{i}}-\overline{\mathrm{j}}+\overline{\mathrm{k}}, \overline{\mathrm{i}}-3 \overline{\mathrm{j}}-5 \overline{\mathrm{k}}, 3 \overline{\mathrm{i}}-4 \overline{\mathrm{j}}-4 \overline{\mathrm{k}}\) అనే బిందువులు లంబకోణ త్రిభుజం శీర్షాలవుతాయని చూపి ఆ త్రిభుజం మిగతా కోణాలను కనుక్కోండి.
సాధన:
‘O’ మూలబిందువు. A, B, C లు దత్త బిందువులు.

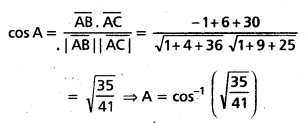
ప్రశ్న 10.
ఒక ఘనంలో రెండు కర్ణాల మధ్య చిన్న కోణం 9 అయితే cos θ = \(\frac{1}{3}\) అవుతుందని నిరూపించండి. [May 11]
సాధన:
ఘనం యూనిట్. ఘనం అనుకొందాం.

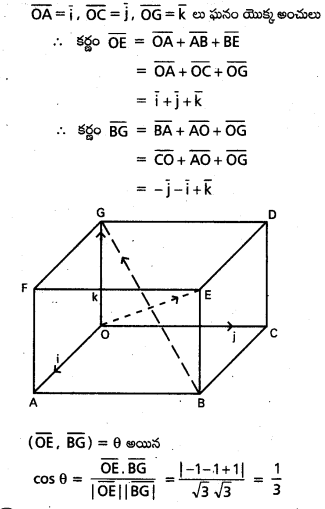
ప్రశ్న 11.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) కౌలు పరస్పరం లంబంగా ఉండే శూన్యేతర సదిశలు \(x \bar{a}+y \bar{b}+z \bar{c}=0\) అయితే x = y = z = 0 అని చూపండి.
సాధన:

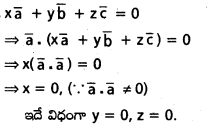
ప్రశ్న 12.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు సమాన పరిమాణం గల పరస్పర లంబ సదిశలైతే, \(\overline{\mathrm{a}}+\overline{\mathrm{b}}+\overline{\mathrm{c}}\) సదిశ, a, b, c లలోని ప్రతి సదిశతోను cos^-1 \(\left(\frac{1}{\sqrt{3}}\right)\) కోణం చేస్తుందని చూపండి.
సాధన:
\(|\bar{a}|=|\bar{b}|=|\bar{c}|\) = λ, అనుకొందాం.
\(|\bar{a}+\bar{b}+\bar{c}|^2\) = a² + b² + c² + 2 Σ \((\bar{a} \cdot \bar{b})\)

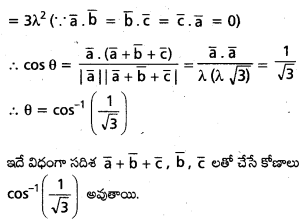
ప్రశ్న 13.
ABCD సమాంతర చతుర్భుజంలో \(\overline{\mathrm{A B}}=\mathrm{3} \overline{\mathrm{i}}-2 \overline{\mathrm{j}}+2 \overline{\mathrm{k}}\), \(\overline{A D}=\bar{i}-2 \bar{k}\) లు ఆసన్న భుజాలు అయితే, కర్ణాల మధ్య కోణాన్ని కనుక్కోండి.
సాధన:

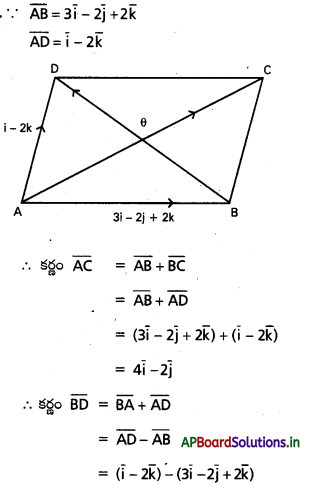
ప్రశ్న 14.
ఏవైనా రెండు సదిశలు a, లకు కింది వాటిని నిరూపించండి.
i) |a.b| ≤ |a||b|(కౌషి-స్క్వార్జ్ అసమానత)
ii) |a + b| ≤ |a| + |b| (త్రిభుజ అసమానత)
సాధన:
i) a = 0 లేదా b = 0 అయితే, రెండు అసమానతలు వర్తిస్తాయి. వివరణ అవసరం లేదు.
అందువల్ల |a| ≠ 0 ≠ |b|అనుకుందాం.
అప్పుడు \(\frac{|a \cdot b|}{|a||b|}\) = |cos θ| ≤ 1.
కాబట్టి |a . b|≤ |a| |b|

ii) |a + b|² = ( a + b) ²
(a + b). (a + b)
= a.a + a.b + b.a + b.b
= |a|² + 2|a. b| + |b|²
(అదిశా లబ్ధం వినిమయం)
≤ |a|² + 2|a. b| + |b|²
(∵ x< |x| ∀ x ∈ R)
≤ |a|² + 2|a| |b|+|b|² ((i) నుంచి)
= (|a| + |b|)²
కాబట్టి |a + b| ≤ |a| + |b|.

ప్రశ్న 15.
(−2, 1, 3) బిందువు గుండా పోతూ \(3 \overline{\mathrm{i}}+\overline{\mathrm{j}}+5 \overline{\mathrm{k}}\) సదిశకు లంబంగా ఉండే తలం సమీకరణం కార్టీసియన్ సమీకరణాన్ని కనుక్కోండి.
సాధన:

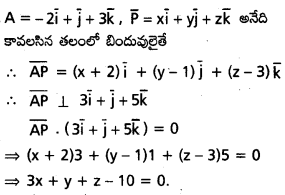
ప్రశ్న 16.
4x – 12y – 32 – 7 = 0 తలానికి సమాంతరంగా ఉంటూ, A (2, -1, -4) బిందువు గుండా పోయే తలానికి కార్టీసియన్ సమీకరణం కనుక్కోండి.
సాధన:
4x – 12y − 3z – 7 = 0 తలానికి సమాంతరంగా ఉండే తలం సమాకరణం
4x – 12y – 3z = p అనుకొందాము.
∴ A(2, – 1, -4) గుండా పోతుంది కనుక
⇒ 4(2) – 12(-1) – 3(-4) = p
⇒ p = 32
∴ కావలసిన తలం సమీకరణం
4x – 12y – 3z = 32

ప్రశ్న 17.
2x – 3y – 6z = 5, 6x + 2y – 9z = 4 సమీకరణాలు సూచించే తలాల మధ్యకోణం కనుక్కోండి.
సాధన:
తలం సమీకరణం 2x – 3y – 6z = 5

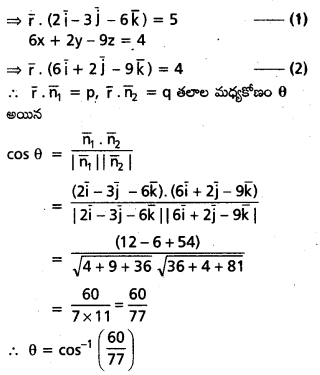
ప్రశ్న 18.
\(2 \bar{i}+\bar{j}+\bar{k}, \bar{i}-\bar{j}+\bar{k}\) సదిశలతో సతలీయం అవుతూ, \(3 \bar{i}+2 \bar{j}+6 \bar{k}\). సదిశలకు లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
సాధన:

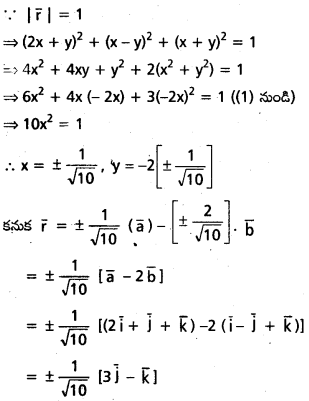
ప్రశ్న 19.
\(\bar{a}=2 \bar{j}-3 \bar{j}+5 \bar{k}, \bar{b}=-\bar{j}+4 \bar{j}+2 \bar{k}\) అయితే, \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}\) ను కనుక్కోండి. \(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) లు రెండింటికీ లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
సాధన:

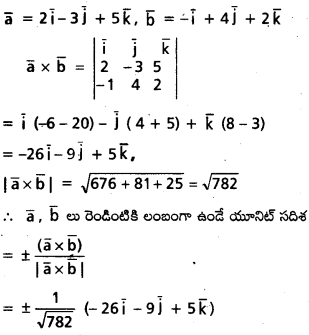
ప్రశ్న 20.
\(\overline{\mathrm{a}}=2 \bar{i}-3 \bar{j}+5 \bar{k}, \bar{b}=-\bar{i}+4 \bar{j}+2 \bar{k}\) అయితే \((\overline{\mathrm{a}}+\overline{\mathrm{b}}) \times(\overline{\mathrm{a}}-\overline{\mathrm{b}})\) ని \(\overline{\mathrm{a}}+\overline{\mathrm{b}} ; \overline{\mathrm{a}}-\overline{\mathrm{b}}\) సదిశలు రెండింటికీ లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
సాధన:
\(\bar{a}=2 \bar{i}-3 \bar{j}+5 \bar{k}\)
\(\overline{\mathrm{b}}=-\overline{\mathrm{i}}+4 \bar{j}+2 \bar{k}\)
\((\bar{a}+\bar{b}) \times(\bar{a}-\bar{b})\)

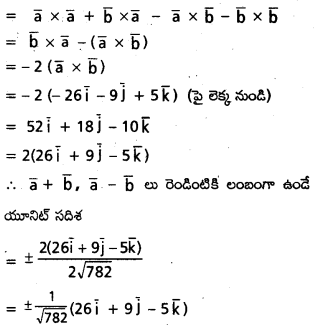
ప్రశ్న 21.
\(\overline{\mathrm{a}}=\mathrm{2} \overline{\mathrm{i}}-\mathrm{3} \overline{\mathrm{j}}, \overline{\mathrm{b}}=\mathrm{3} \overline{\mathrm{i}}-\overline{\mathrm{k}}\) సదిశలు ఆసన్న భుజాలుగా గల సమాంతర చతుర్భుజం వైశాల్యం కనుక్కోండి. [Mar. 08: May 08]
సాధన:
సమాంతర చతుర్భుజి సదిశా వైశాల్యం

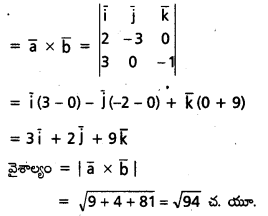
ప్రశ్న 22.
a × b = c × d, a × c = b × d అయ్యేటట్లు a, b, c, d ఉంటే, a – d, b – c సదిశలు సమాంతరమని చూపండి.
సాధన:

ప్రశ్న 23.
\(\overline{\mathrm{a}}=\overline{\mathrm{i}}+\mathrm{2} \overline{\mathrm{j}}+\mathrm{3} \overline{\mathrm{k}}, \overline{\mathrm{b}}=\mathrm{3} \overline{\mathrm{i}}+\mathrm{5} \overline{\mathrm{j}}-\overline{\mathrm{k}}\) సదిశలు త్రిభుజం రెండు భుజాలయితే, ఆ త్రిభుజ వైశాల్యాన్ని కనుక్కోండి.
సాధన:

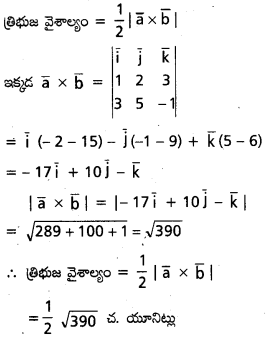
ప్రశ్న 24.
త్రిభుజం ABC లో \(\overline{\mathrm{B C}}=\overline{\mathrm{a}} ; \overline{\mathrm{C A}}=\overline{\mathrm{b}}, \overline{\mathrm{A B}}=\overline{\mathrm{c}}\) అయితే \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}=\overline{\mathrm{b}} \times \overline{\mathrm{c}}=\overline{\mathrm{c}} \times \overline{\mathrm{a}}\) అని చూపండి.
సాధన:

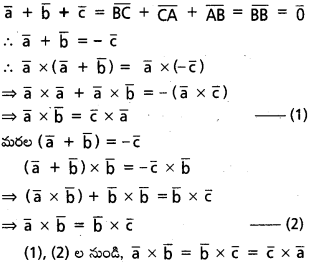
ప్రశ్న 25.
\(\overline{\mathrm{a}}=\mathrm{2} \overline{\mathrm{i}}-\overline{\mathrm{j}}+\overline{\mathrm{k}}, \overline{\mathrm{b}}=\mathrm{3} \overline{\mathrm{i}}+\mathrm{4} \overline{\mathrm{j}}-\overline{\mathrm{k}}\) సదిశల మధ్య కోణం 8 అయితే, sin θ విలువను కనుక్కోండి.
సాధన:

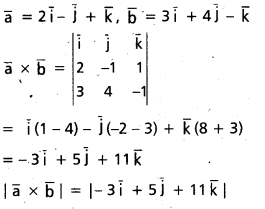
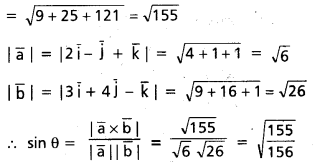
ప్రశ్న 26.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) సదిశలతో 3o \(\overline{\mathrm{c}}\) ≠ 0, \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}=\overline{\mathrm{c}}\), \(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) అయితే \(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు జతలుగా పరస్పర లంబ సదిశలని చూపి, \(|\bar{b}|=1,|\bar{c}|=|\bar{a}|\) అని రుజువు చేయండి.
సాధన:

ప్రశ్న 27.
\(\bar{a}=2 \bar{i}+\bar{j}-2 \bar{k}, \bar{b}=\bar{i}+\bar{j}\) అనుకొందాం. \(\bar{a} \cdot \bar{c}=|\bar{c}|,|\bar{c}-\bar{a}|=2 \sqrt{2}, \bar{a} \times \bar{b}\) మరియు \(\overline{\mathrm{c}}\) ల మధ్య కోణం 30° అయ్యేటట్లు సదిశ C ఉంటే, \(|(\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \times \bar{c}|\) విలువను కనుక్కోండి.
సాధన:

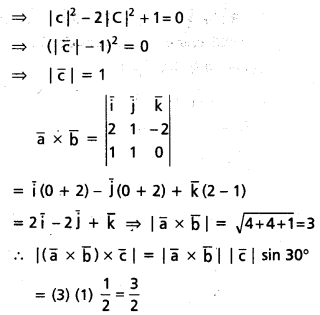
ప్రశ్న 28.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) లు సరేఖీయాలు కాని యూనిట్ సదిశలు. \(\bar{\alpha}=\overline{\mathrm{a}}-(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}) \overline{\mathrm{b}}, \bar{\beta}=\overline{\mathrm{a}} \times \overline{\mathrm{b}}\) అయితే \(|\bar{\beta}|=|\bar{\alpha}|\) అని చూపండి.
సాధన:

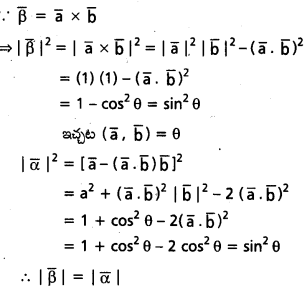
ప్రశ్న 29.
\(\overline{\mathrm{i}}, \overline{\mathrm{i}}+\overline{\mathrm{j}}\) లతో నిర్ధారితమైన తలం \(\overline{\mathrm{i}}-\overline{\mathrm{j}}, \overline{\mathrm{i}}+\overline{\mathrm{k}}\) సదిశలు నిర్ధేశించే తలాల ఖండన రేఖకు సమాంతరంగా ఉండే సదిశ ā అయితే, \(\overline{\mathrm{a}}, \overline{\mathrm{i}}-2 \overline{\mathrm{j}}+2 \overline{\mathrm{k}}\) సదిశల మధ్యకోణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 30.
\(\overline{\mathrm{a}}=4 \overline{\mathrm{j}}+5 \overline{\mathrm{j}}-\overline{\mathrm{k}}, \overline{\mathrm{b}}=\overline{\mathrm{i}}-4 \overline{\mathrm{j}}+5 \overline{\mathrm{k}}\), \(\overline{\mathrm{c}}=3 \overline{\mathrm{i}}+\overline{\mathrm{j}}-\overline{\mathrm{k}}\) అనుకొందాం. \(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) లు రెండిటికి లంబంగా ఉంటూ \(\bar{\alpha} \cdot \overline{\mathrm{c}}\) = 21 అయ్యేలా ఉండే λ ను కనుక్కోండి.
సాధన:

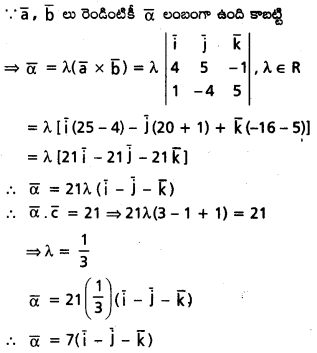
ప్రశ్న 31.
ఏదైనా ఒక సదిశ a కి |a × i|² + |a × j|² + |a × k|² = 2|a|² అని చూపండి.
సాధన:
a = x i + y j + z k అనుకుందాం.
∴ a × i = – yk + zj.
∴ |a × i|² = y² + z²
ఇదే విధంగా |a × j|² = z² + x², |a × k|²
= x² + y²
∴ |a × i|² + |a × j|² + |a × k|² = 2(x² + y² + z²) = 2|a|²

ప్రశ్న 32.
\(\overline{\mathrm{a}} \neq \mathrm{0}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) సదిశలు \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}=\overline{\mathrm{a}} \times \overline{\mathrm{c}}\), \(\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}=\overline{\mathrm{a}} \cdot \overline{\mathrm{c}}\) అవుతూ ఉంటే, \(\overline{\mathrm{b}}=\overline{\mathrm{c}}\) అవుతుందని చూపండి.
సాధన:

ప్రశ్న 33.
\(\overline{\mathrm{a}}=2 \overline{\mathrm{i}}-\overline{\mathrm{j}}+\bar{k}, \overline{\mathrm{b}}=\bar{i}-3 \bar{j}-5 \bar{k}, \bar{c}\) = \(3 \bar{i}-4 \bar{j}-4 \bar{k}\) సదిశలు సతలీయ సదిశలవుతాయని చూపండి.
సాధన:
(a × b). c = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & -3 & -5 \\
3 & -4 & -4
\end{array}\right|\)
(i, j, k) కుడిచేతి పద్ధతిలోని లంబ యూనిట్ సదిశాత్రయం
a = a₁i+ a₂j + a₃k
b = b₁i + b₂j + b₃k
c = c₁i + c₂j + c₃k
[a, b, c] = \(\left|\begin{array}{lll}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|\)
= 2(12 – 20) + (-4 + 15) + (-4 + 9)
= – 16 + 11 + 5 = 0.
∴ [a, b, c] లు సతలీయ సదిశలు
a = a₁i + a₂j + a₃k,
b = b₁i + b₂j + b₃k,
c = c₁i + c₂j + c₃k అయితే , a, b, c సతలీయ కావడానికి ఆవశ్యక, పర్యాప్త నియమం
\(\left|\begin{array}{lll}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|\) = 0

ప్రశ్న 34.
\(2 \overline{\mathrm{i}}-3 \overline{\mathrm{j}}+\overline{\mathrm{k}}, \overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}, 2 \overline{\mathrm{i}}+\overline{\mathrm{j}}-\overline{\mathrm{k}}\) లు సహావసానికి భుజాలుగా గల సమాంతర ఫలక ఘనపరిమాణాన్ని కనుక్కోండి.
సాధన:

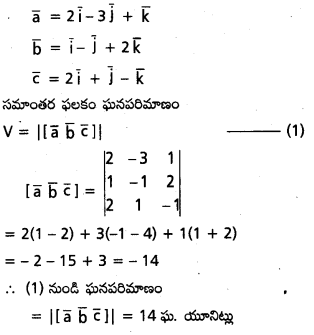
ప్రశ్న 35.
\(\bar{a}=2 \bar{i}-\bar{j}+\bar{k}, \bar{b}=\bar{i}+2 \bar{j}-3 \bar{k}\), \(\overline{\mathrm{c}}=3 \overline{\mathrm{i}}+p \overline{\mathrm{j}}+5 \overline{\mathrm{k}}\) సదిశలు సతలీయాలైతే విలువను కనుక్కోండి.
సాధన:
∴ \(\bar{a}, \bar{b}, \bar{c}\) లు సతలీయాలు.
⇒ \([\bar{a} \bar{b} \bar{c}]\) = 0
⇒ \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & -3 \\
3 & p & 5
\end{array}\right|\) = 0
⇒2(10 + 3p) + 1 (5 + 9) + 1(p 6) = 0
⇒ 20 + 6p + 14 + p – 6 = 0
⇒ 7p + 28 = 0
∴ p = – 4

ప్రశ్న 36.
\(\overline{\mathrm{i}} \times(\overline{\mathrm{a}} \times \overline{\mathrm{j}})+\overline{\mathrm{j}} \times(\overline{\mathrm{a}} \times \overline{\mathrm{j}})+\mathrm{k} \times(\overline{\mathrm{a}} \times \overline{\mathrm{k}})=\mathrm{2} \overline{\mathrm{a}}\) అని చూపండి
సాధన:

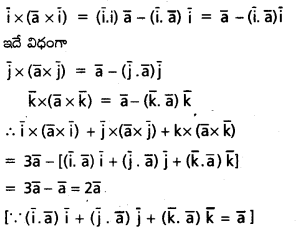
ప్రశ్న 37.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు మూడు సదిశలైతే, \(\left[\begin{array}{lll}
\bar{b}+\bar{c} & \bar{c}+\overline{\mathrm{a}} & \overline{\mathrm{a}}+\overline{\mathrm{b}}
\end{array}\right]=2\left[\begin{array}{lll}
\overline{\mathrm{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}}
\end{array}\right]\) అని చూపండి.
సాధన:

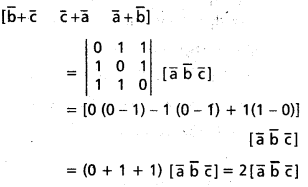
ప్రశ్న 38.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు మూడు సదిశలైతే. \(\left[\begin{array}{lll}
\overline{\mathrm{b}} \times \overline{\mathrm{c}} & \overline{\mathrm{c}} \times \overline{\mathrm{a}} & \overline{\mathrm{a}} \times \overline{\mathrm{b}}
\end{array}\right]=\left[\begin{array}{lll}
\overline{\mathrm{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}}
\end{array}\right]^2\) అని చూపండి.
సాధన:

ప్రశ్న 39.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు యూనిట్ సదిశలు \(\bar{b}, \bar{c}\) సమాంతరాలు కావు. \(\bar{a} \times(\bar{b} \times \bar{c})=\frac{1}{2} \bar{b}\) అయితే, \(\overline{\mathrm{a}}\) సదిశ \(\overline{\mathrm{b}}, \overline{\mathrm{c}}\) లతో చేసే కోణాలను కనుక్కోండి.
సాధన:

ప్రశ్న 40.
\(\overline{\mathrm{a}}=\overline{\mathrm{i}}+\overline{\mathrm{j}}+\overline{\mathrm{k}}, \overline{\mathrm{b}}=2 \overline{\mathrm{i}}, \overline{\mathrm{j}}+\mathrm{3} \overline{\mathrm{k}}, \overline{\mathrm{c}}=\overline{\mathrm{i}}-\overline{\mathrm{j}}\) , \(\overline{\mathrm{d}}=\mathrm{6} \overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}\) అయితే \(\overline{\mathrm{b}} \times \overline{\mathrm{c}}, \overline{\mathrm{c}} \times \overline{\mathrm{a}}\), \(\overline{\mathrm{a}} \times \overline{\mathrm{b}}\) లలో \(\overline{\mathrm{d}}\) రాయండి . [May ’12]
సాధన:

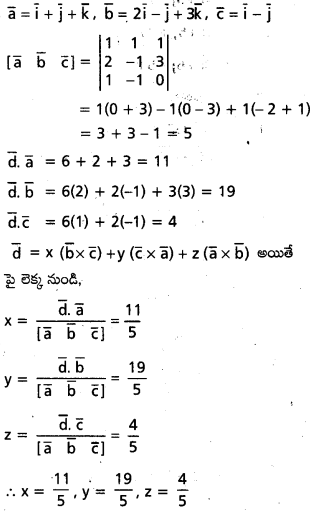
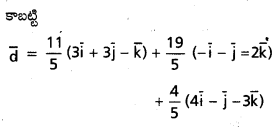
ప్రశ్న 41.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}, \overline{\mathrm{d}}\) లు నాలుగు సదిశలైతే, \((\overline{\mathrm{b}} \times \overline{\mathrm{c}}) \cdot(\overline{\mathrm{a}} \times \overline{\mathrm{d}})+(\overline{\mathrm{c}} \times \overline{\mathrm{a}}) \cdot(\overline{\mathrm{b}} \times \overline{\mathrm{d}})\) + \((\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \cdot(\overline{\mathrm{c}} \times \overline{\mathrm{d}})\) = 0 అని చూపండి.
సాధన:

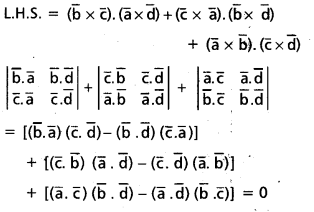
ప్రశ్న 42.
A = (2, 3, -1), B = (4, 5, 2), C = (3, 6, 5) బిందువుల గుండాపోయే తలం సమీకరణం కనుక్కోండి.
సాధన:
‘O’ మూలబిందువు.

ప్రశ్న 43.
A (3, -2, -1) గుండాపోయే \(\overline{\mathrm{b}}=\overline{\mathrm{i}}-2 \bar{j}+4 \bar{k}\), \(\overline{\mathrm{c}}=\mathrm{3 i}+2 \bar{j}-5 \bar{k}\) సదిశలకు సమాంతరంగా ఉండే తలం సమీకరణం కనుక్కోండి.
సాధన:

i.e., 2x + 17y + 8z + 36 = 0. ఇదియే కాలవసిన తలం సమీకరణం

ప్రశ్న 44.
r. (i + j + k) = 6, r. (2i + 3j+ 4k) = -5 తలాల ఛేదన రేఖ గుండా (1, 1, 1) బిందువు గుండా పోయే తలం సదిశా సమీకరణాన్ని కనుక్కోండి.
సాధన:
ఇక్కడ n₁ = i + j + k and n₂ = 2i + 3j + 4k; ఇంకా d₁ = 6, and d₂ = -5. ఈ విలువలను
r.(n₁ + λn₂) = d₁ + λd₂ సంబంధంలో ప్రతిక్షేపిస్తే r.[(i + j + k + λ (2i + 3j + 4k)] = 6 – 5λ లేదా . [(1 + 2λ)i + (1 + 3λ)j + (1 + 4λ)k]
= 6 – 5λ, λ ఒక వాస్తవ సంఖ్య ………….. (1)
r = xi + yj + zk గా తీసుకుంటే
(xi + yj + zk). [(1 + 2λ)i + (1 + 3λ)j + (1 + 4λ)k] = 6 – 5λ
లేదా (1 + 2λ)x + (1 + 3λ) y + (1 + 4λ)z = 6 – 5λ
(x + y + z – 6) + λ (2x + 3y + 4z + 5) = 0 ………………. (2)
ఈ తలం (1, 1, 1) బిందువు గుండాపోతుంది. కాబట్టి అది సమీకరణం (2)ని తృప్తిపరుస్తుంది. అప్పుడు (1 + 1 + 1 – 6) + λ (2 + 3 + 4 + 5) = 0
⇒ λ = \(\frac{3}{14}\)
ఈ λ విలువను సమీకరణం (1)లో ప్రతిక్షేపిస్తే,

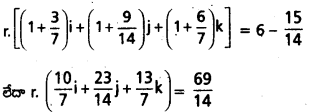
లేదా r. (20i + 23j + 26k) = 69.
ఇదే కావలసిన లం సదిశా సమీకరణం.

ప్రశ్న 45.
r. (6i – 3j + 2k) = 4 తలం నుంచి (2, 5, -3) బిందువునకు గల దూరాన్ని కనుక్కోండి.
సాధన:
ఇక్కడ a = 2i + 5j – 3k, N = 6i – 3j + 2k; d = 4.
∴ దత్త తలం నుంచి (2, 5, -3) బిందువునకు దూరం

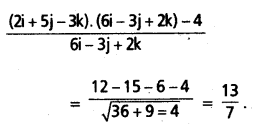
ప్రశ్న 46.
\(\frac{x+1}{2}=\frac{y}{3}=\frac{z-3}{6}\) రేఖకు 10x + 2y – 11z = 3 తలానికి మధ్యకోణాన్ని కనుక్కోండి.
సాధన:
దత్తరేఖకి, తలం లంబానికి మధ్య కోణం అనుకొందాం.
దత్తసమీకరణాలను సదిశా రూపంలోకి మారిస్తే,
r = (-i + 3k) + λ(2i + 3j. + 6k)
లేదా (10i + 2j – 11k) = 3.
ఇక్కడ b = 2i + 3j + 6k, n = 10i + 2j – 11k.

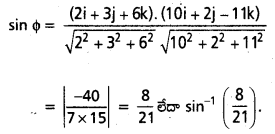
ప్రశ్న 47.
a, b, c, d ఏవైనా నాలుగు సదిశలైతే, (a × b) × (c × d) = [a c d]b – [b c d]a and (a × b) × (c × d) = [a b d]c – [a b c] d.
సాధన:
m = c × d అనుకొందాం
∴ (a × b) × (c × d) = (a × b) × m
= (a.m)b – (b.m)a
= (a. (c × d))b (b. (c × d)) a
= [a c d]b – [b c d]a.
ఇప్పుడు a × b = n అనుకొందాం.
∴ (a × b) × (c × d) n × (c × d)
= (n . d)c – (n.c)d
= ((a × b). d) c – ((a × b). c)d
= [a b d]c – [a b c]d.
∴ (acd]b – [bcd]a = (a × b) × (c × d) = [abd]c – [abc]d.

ప్రశ్న 48.
\(\overline{\mathrm{r}}=(6 \overline{\mathrm{i}}+2 \bar{j}+2 \bar{k})+t(\bar{i}-2 \bar{j}+2 \bar{k})\), \(\overline{\mathrm{r}}=(-4 \overline{\mathrm{i}}-\overline{\mathrm{k}})+5(3 \overline{\mathrm{i}}-2 \overline{\mathrm{j}}-2 \overline{\mathrm{k}})\) సూచించే రేఖలు మధ్య కనిష్ట దూరాన్ని కనుక్కోండి.
సాధన:

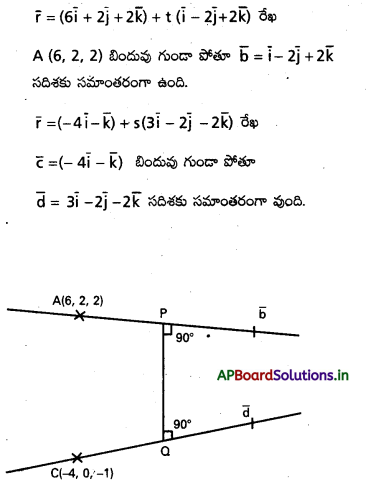
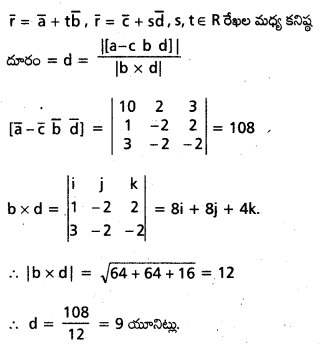
ప్రశ్న 49.
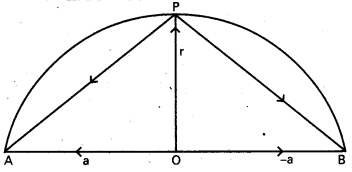
అర్ధవృత్తంలో కోణం లంబకోణం అవుతుంది. [May ’08]
సాధన:
కేంద్రం గల వృత్త వ్యాసం AB అనుకొందాం.
OA = a అనుకొంటే OB = – a అవుతుంది.
అర్థవృత్తం మీద, OP = r అవుతూ P ఒక బిందువు
అప్పుడు PA . PB = (a – r) . (-a – r)
= -(a² – r²)
= 0 (∵|a| = |r| = వ్యాసార్థం)
∴ ∠APB = 90°.

ప్రశ్న 50.
i) త్రిభుజంలో, ఉన్నతులు (altitudes) అనుషక్తాలు.
ii) త్రిభుజంలో, భుజాల లంబ సమద్విఖండన రేఖలు అనుషక్తాలు. [Mar. ’13]
సాధన:
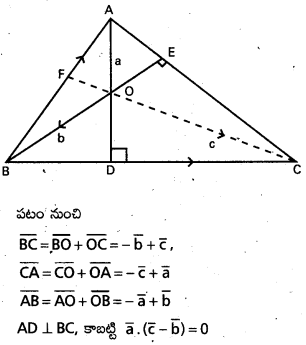
i) దత్త త్రిభుజం ABC లో A, B ల నుంచి వరుసగా BC, CA లకు గీసిన ఉన్నతులు, వాటిని D, E ల వద్ద ఖండిస్తున్నాయనుకొందాం. AD, BE లు 0 వద్ద ఖండించుకొంటాయనుకొని, CO ను కలిపి అది AB ని F వద్ద కలుసుకొనేటట్లు పొడిగిద్దాం. O దృష్ట్యా, A, B, C స్థానసదిశలను వరుసగా \(\bar{a}, \bar{b}, \bar{c}\) అనుకొందాం.




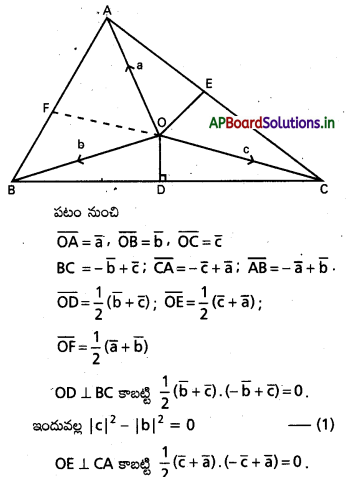
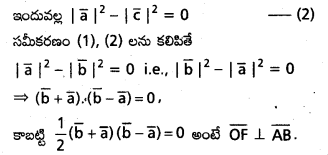
∴ త్రిభుజంలో భుజాల లంబ సమద్విఖండన రేఖలు అనుషక్తాలు.

ప్రశ్న 51.
A, B, C, D శీర్షాలు అపసవ్య దిశలో ఉండేటట్లు ABCD సమాంతర చతుర్భుజం అయితే, కర్ణాలు AC, BDలలో ABCD సమాంతర చతుర్భుజం సదిశా వైశాల్యం \(\frac{1}{2}\) (AC × BD) అని చూపండి.
సాధన:

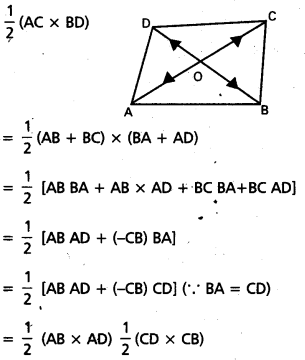
= ∆ ABC సదిశా వైశాల్యం + ∆CDB సదిశా వైశాల్యం ∆BCD సమాంతర చతుర్భుజ సదిశా ‘ వైశాల్యం

ప్రశ్న 52.
ఏదైనా సదిశలు a, b, c కి (a × b) × c = (a.c) b – (b.c) a [(A.P) Mar. 15; May ’06; June ’04]
సాధన:
(a × b) × c = (a.c) b – (b.c) a

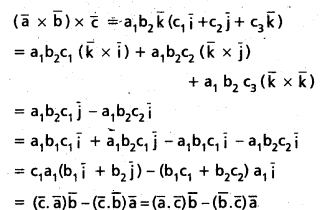
ప్రశ్న 53.
a, b, c, d లు నాలుగు సదిశలైతే (a × b) , (c × d) = \(\left|\begin{array}{ll}
a \cdot c & a \cdot d \\
b . c & b \cdot d
\end{array}\right|\) అని చూపండి (a × b)² = a² b² – (a . b)²
సాధన:

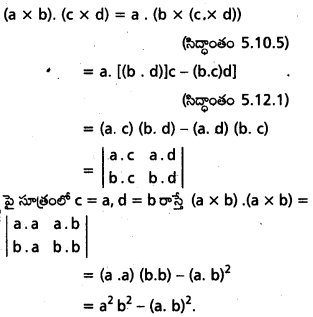
ప్రశ్న 54.

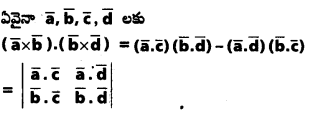
సాధన:

ఈ ఫలితం ఒక అదిశ. కాబట్టి దీన్ని నాలుగు సదిశ అదిశ లబ్ధం అని కూడా అంటాం.