AP Inter 1st Year Physics Notes Chapter 7 కణాల వ్యవస్థలు, భ్రమణ గమనం

Students can go through AP Inter 1st Year Physics Notes 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం will help students in revising the entire concepts quickly.

AP Inter 1st Year Physics Notes 7th Lesson కణాల వ్యవస్థలు, భ్రమణ గమనం

→ నియమిత కాలంలో సదిశ త్రిజ్య తిరిగిన కోణమును కోణీయ స్థానభ్రంశము అంటారు.

→ కోణీయ స్థానభ్రంశపు రేటు కోణీయ వేగము ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)

→ కోణీయ వేగపు రేటు కోణీయ త్వరణం a = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)

→ వస్తువుపై పనిచేయు బలము వలన, బలపరిమాణంతో నిమిత్తం లేకుండా వస్తువు ఆకారంలో మార్పు లేకుండా, వస్తువులోని వివిధ కణముల మధ్య దూరము స్థిరముగా ఉంటే, ఆ వస్తువును దృఢవస్తువు అంటారు.

→ ఒక వస్తువుపై రెండు సమాన బలాలు సమాంతరంగా ఉండి వ్యతిరేక దిశలలో, బల ప్రయోగ దిశలు వేరుగా పనిచేసిన ఆ వ్యవస్థను బలయుగ్మం అంటారు.

→ సమాంతర బల నియమాలు
(a) ఒక దిశలో పనిచేయు బలాల మొత్తం దాని వ్యతిరేక దిశలో పనిచేయు బలాల మొత్తమునకు సమానము.
(b) ఒకే బిందువు ఆధారంగా సవ్యదిశలో పనిచేయు భ్రామకాల మొత్తం, అపసవ్యదిశలో పనిచేయు భ్రామకాల మొత్తమునకు సమానము.

→ అభికేంద్ర బలం (F_c) : ఒక కణం వృత్తాకార చలనాన్ని చేయుటకు అవసరమయ్యే బలాన్ని అభికేంద్ర బలం అంటారు. దీని పరిమాణం \(\frac{M v^2}{r}\) (లేదా) Mrω² దీని దిశ కూడా కేంద్రం వైపుకు ఉంటుంది మరియు ఇది ఒక చలరాశి. గురుత్వాకర్షణ బలం, స్థిర విద్యుత్ బలం, ఘర్షణ బలం మొదలగు బలాల వలె ఇది కూడా ఒక యథార్థ బలం. బాహ్య కారకం వల్ల ఇది కణానికి అందచేయబడుతుంది.

→ గట్టు కట్టబడిన రోడ్డుపై సురక్షిత గరిష్ఠ వడి V = \(\sqrt{r g \mu}\)

→ క్షితిజ సమాంతర వృత్తాకార చలనంలో ఉన్న వస్తువు వడి అన్ని బిందువుల వద్ద సమానంగా ఉంటుంది.

→ ఒక రాయిని తాడుకు చివరగా కట్టి, దానిని క్షితిజ సమాంతర వృత్తంలో తిప్పితే, తాడుపై తన్యత = అభికేంద్ర బలం = \(\frac{M v^2}{r}\) = mrω²

→ ఒక వస్తువు భ్రమణ చలనంలో ఉంటే, వస్తువులోని ప్రతీ కణం వృత్తాకార మార్గంలో చలిస్తుంది. ఇలాంటి వృత్తాల కేంద్రాలన్ని ఒకే సరళరేఖపై ఉంటాయి. ఈ సరళరేఖను భ్రమణాక్షం అంటారు.

→ భ్రమణ చలనంలో ఉన్న వస్తువులోని అన్ని కణాలు ఒకే కోణీయ స్థానభ్రంశాన్ని, ఒకే కోణీయ వేగాన్ని మరియు ఒకే కోణీయ త్వరణాన్ని కలిగి ఉంటాయి.

→ బలం మరియు ఒక బిందువు నుండి బలప్రయోగ బిందువుకు మధ్య లంబ దూరాల లబ్ధాన్ని టార్క్ లేదా బలభ్రామకం అని అంటారు. సదిశా రూపంలో τ = r × F.
టార్క్ SI ప్రమాణం Nm, మితి ఫార్ములా [M L²T^-2].

→ పరిమాణంలో సమానంగా, దిశలో వ్యతిరేకంగా ఉండి సరేఖీయం కాని రెండు బలాలు బలయుగ్మాన్ని ఏర్పరుస్తాయి. రెండు బలాల మధ్య లంబ దూరం మరియు ఆ రెండింటిలో ఏదో ఒక బలం పరిమాణంల లబ్ధాన్ని బలయుగ్మ భ్రామకం లేదా బలయుగ్మ టార్క్ అంటారు.

→ ఒక దృఢ వస్తువును ఏర్పరుస్తున్న వివిధ కణాల ద్రవ్యరాశులు మరియు భ్రమణాక్షం నుండి వాటి లంబ దూరాల వర్గాల లబ్దాల మొత్తాన్ని ఆ అక్షం పరంగా దృఢ వస్తువు యొక్క జఢత్వ భ్రామకం అని నిర్వచిస్తాము. m ద్రవ్యరాశి గల బిందు రూప ద్రవ్యరాశి జఢత్వ భ్రామకం I ఇక్కడ r అనునది భ్రమణాక్షం నుండి బిందురూప ద్రవ్యరాశి లంబ దూరం.

→ దృఢ వస్తువు జఢత్వ భ్రామకం I = \(\sum_{i=1}^n m_i r_i^2\) ఇక్కడ i వ కణం ద్రవ్యరాశి mi మరియు భ్రమణాక్షం నుండి
iవ కణం లంబ దూరం r_i, జఢత్వ భ్రామకం SI ప్రమాణం kg m², మితి ఫార్ములా [ML²T°).

→ వస్తువు మొత్తం ద్రవ్యరాశి ఏ బిందువు వద్ద కేంద్రీకరింపబడి ఉంటుందో మరియు ద్రవ్యరాశి వితరణతో దాని జఢత్వ భ్రామకం సమానమవుతుందో ఆ బిందువుకు మరియు భ్రమణాక్షానికి మధ్యగల దూరాన్ని భ్రమణ వ్యాసార్థం అంటారు.

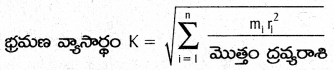
→ జఢత్వ భ్రామకం మరియు భ్రమణ వ్యాసార్థాలు రెండూ భ్రమణాక్షం స్థానంపై మరియు భ్రమణాక్షం చుట్టూ ద్రవ్యరాశి వితరణపై ఆధారపడి ఉంటాయి. కాని జఢత్వ భ్రామకం ద్రవ్యరాశిపై కూడా ఆధారపడి ఉంటుంది.

→ సమాంతరాక్ష సిద్ధాంతం : ఏదైన ఒక అక్షం పరంగా దృఢ వస్తువు జఢత్వ భ్రామకం, దాని ద్రవ్యరాశి కేంద్రం గుండా పోయే సమాంతర అక్షం పరంగా దాని జఢత్వ భ్రామకం మరియు వస్తు ద్రవ్యరాశి, రెండు సమాంతరాక్షాల మధ్య దూరం వర్గాల లబ్ధాల మొత్తానికి సమానం. ఏదేని ఒక అక్షం పరంగా దృఢ వస్తువు జఢత్వ భ్రామకం I₀ = I_c + Mr². ఇక్కడ I_G అనేది వస్తు ద్రవ్యరాశి కేంద్రం గుండాపోతున్న సమాంతర అక్షం పరంగా దాని జఢత్వ భ్రామకం మరియు రెండు సమాంతరాక్షాల మధ్య దూరం r.

→ ఒక సమతల పటలం తలానికి లంబంగా ఉన్న అక్షం పరంగా దాని జఢత్వ భ్రామకం, ఆ పటలం తలంలో పరస్పరం లంబంగా ఉండి ఒక బిందువు వద్ద ఖండించుకుంటున్న రెండు అక్షాల పరంగా దాని జఢత్వ భ్రామకాల మొత్తానికి సమానం.

→ కోణీయ ద్రవ్యవేగము, L = mvr, ఇచ్చట m కణ ద్రవ్యరాశి, V వేగము మరియు r లంబదూరము.

→ కోణీయ ద్రవ్యవేగము L = Iω.

→ T మరియు ల మధ్య సంబంధం T = \(\frac{\mathrm{dL}}{\mathrm{dt}}\) మరియు T, α ల మధ్య సంబంధం T = Iα.

→ కోణీయ ద్రవ్యవేగ నిత్యత్వ సూత్రము : ఒక భ్రమణ వ్యవస్థపై బాహ్య బలం పనిచేయకపోతే, వ్యవస్థ ద్రవ్యవేగము పరిమాణంలో మరియు దిశలో స్థిరము.

→ ఫలిత బాహ్య టార్క్ సున్నా అయితే, L స్థిరాంకం, i.e., Iω = స్థిరాంకం (లేక) ω, I కి విలోమానుపాతంలో ఉండును.

→ తీగ ఒక చివర వస్తువును కట్టి నిలువు వృత్తంలో త్రిప్పితే, గురుత్వం వల్ల వేగం మారును.

→ వస్తువు నిలువు వృత్తంలో గరిష్ట బిందువు వద్ద ఉన్నప్పుడు, తీగలో తన్యత = \(\frac{\mathrm{Mv}_2^2}{\mathrm{r}}\) – Mg, కనిష్ట బిందువు వద్ద ఉన్నప్పుడు తీగలో తన్యత T = \(\frac{\mathrm{Mv}_1^2}{\mathrm{r}}\) + Mg. ఏ స్థానంలో ఉన్నా T = \(\frac{\mathrm{Mv}^2}{\mathrm{r}}\) – Mg cos 6.

→ గరిష్ట బిందువు వద్ద కనిష్ట వేగం v₂ = \(\sqrt{rg}\) కనిష్ట బిందువు వద్ద వేగం v₁ = \(\sqrt{5rg}\)

→ దవ్యరాశి కేంద్రం అనేది కణాల వ్యవస్థ లేదా వస్తువు మొత్తం ద్రవ్యరాశి కేంద్రీకృతమయ్యేటట్లు ప్రవర్తించే బిందువు.

→ ద్రవ్యరాశి కేంద్ర నిరూపకాలు
X_CM = \(\frac{\sum m_i x_i}{\Sigma m_i}\); Y_CM = \(\frac{\Sigma m_i y_i}{\Sigma m_i}\); Z_CM = \(\frac{\Sigma m_i z_i}{\Sigma m_i}\)

→ ద్రవ్యరాశి కేంద్ర వేగము V_CM = \(\frac{m_1 v_1+m_2 v_2}{m_1+m_2}\)

→ ద్రవ్యరాశి కేంద్ర గమనాన్ని వ్యవస్థలోని అంతర్గత బలాలు ప్రభావితం చేయవు.

→ ద్రవ్యరాశి కేంద్రం న్యూటన్ గమన నియమాలను పాటించును.

→ ఒక వస్తువు ద్రవ్యరాశి కేంద్రం వద్ద ద్రవ్యరాశి ఉండవచ్చు లేక ఉండకపోవచ్చును.

→ ఒక వ్యవస్థ యొక్క ద్రవ్యరాశి కేంద్ర రేఖీయ ద్రవ్యవేగం ఆ వ్యవస్థలో ఉండే అన్ని కణాల ద్రవ్య వేగాల మొత్తానికి సమానం.
MV_c = Σ m_iv_i; లేదా P_c = P₁ + P₂ + ……. + P_n
M వ్యవస్థ ద్రవ్యరాశి, v_c ద్రవ్యరాశి కేంద్ర వేగం, p_c ద్రవ్యరాశి కేంద్ర రేఖీయ ద్రవ్యవేగం

→ ఒక బాహ్య బలం F వ్యవస్థకు ఆపాదించిన త్వరణం ఆ వ్యవస్థ ద్రవ్యరాశి కేంద్ర త్వరణానికి సమానం
a_c = \(\frac{1}{M}\) Σa_im_i అంటే Ma_c = F

→ భూమి, చంద్రుడు వ్యవస్థ ద్రవ్యరాశి కేంద్రం భూకేంద్రంనకు దగ్గరగా ఉంటుంది. సూర్యుని వల్ల గురుత్వాకర్షణ బలం ఈ వ్యవస్థ ద్రవ్యరాశి కేంద్రం వద్ద మాత్రమే ప్రయోగింపబడుతున్నట్లుగా భూమి – చంద్రుడు వ్యవస్థ. సూర్యుని చుట్టూ దీర్ఘ వృత్తాకార మార్గంలో తిరుగుతూ ఉంటుంది. ఈ వ్యవస్థ ద్రవ్యరాశి కేంద్రం సూర్యుని చుట్టూ దీర్ఘ వృత్తాకారంలో తిరుగుతూ ఉంటుంది.

→ గాలిలో గమనంలో ఉన్న ఒక గోళం విస్ఫోటనం చెందితే, దాని విస్ఫోటన శకలాలు వేరు వేరు పరావలయ మార్గాల్లో చలిస్తాయి. కాని ఆ గోళం యొక్క ద్రవ్యరాశి కేంద్రం విస్ఫోటనానికి ముందు ఏ పరావలయ మార్గంలో చలిస్తుందో విస్ఫోటనం తరువాత కూడా అదే పరావలయ మార్గంలో చలిస్తుంది.

→ లుడ్విగ్ బోల్ట్ మన్ (1844-1906)
ఆస్ట్రియాలోని వియన్నాలో జన్మించాడు. ఉష్ణగతికశాస్త్ర రెండవ నియమం యొక్క గణాంక అర్థ వివరణను ఎంట్రోపి భావనను బోల్ట్ మన్ సమకూర్చాడు. ఉష్ణోగ్రతలను కలిపే అనుపాత స్థిరాంకానికి బోల్ట్స్ మన్ స్థిరాంకమని ఆయన గౌరవార్థం పేరు పెట్టారు.