AP Inter 1st Year Physics Study Material Chapter 2 ప్రమాణాలు, కొలత

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 2nd Lesson ప్రమాణాలు, కొలత Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 2nd Lesson ప్రమాణాలు, కొలత

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
యధార్థత, ఖచ్చితత్వాల మధ్య తేడాను రాయండి. [May, Mar. ’13]
జవాబు:

యధార్థత	ఖచ్చితత్వం
1) మనం కొలిచే భౌతిక రాశి నిజమైన విలువకు ఎంత దగ్గరగా. ఉన్నది తెలియజేసే ఒక కొలమానమే మనం తీసుకున్న కొలత యొక్క యధార్ధత.	1) ఖచ్చితత్వం అనేది, ఆ పరికరంతో మనం ఎంత కనిష్ఠ అవధి వరకు (లేదా) ఎంత పృథక్కరణం వరకు భౌతికరాశిని కొలవడానికి వీలవుతుందో తెలియ జేస్తుంది.
2) యధార్థత దోషాల మీద ఆధారపడి ఉంటుంది.	2) ఖచ్చితత్వం అనేది దోషాలపై ఆధార పడదు

ప్రశ్న 2.
కొలతలో వచ్చే వివిధ రకాల దోషాలు ఏవి?
జవాబు:
దోషాలు ప్రధానంగా మూడు రకాలు

1. క్రమదోషాలు
2. యాదృచ్ఛిక దోషాలు
3. స్థూల దోషాలు

ప్రశ్న 3.
క్రమదోషాలను ఏవిధంగా కనిష్ఠం చేయవచ్చు లేదా తొలగించవచ్చు? [Mar. ’14]
జవాబు:
ప్రయోగ విధానంలో కౌశలతను పెంచుకోవడం, మంచి పరికరాలను ఎన్నుకోవడం మరియు వీలైనంత వరకు వ్యక్తిగతమైన లోపం లేకుండా చూసుకోవాలి.

ఇవ్వబడిన అమరికకు, ఈ దోషాలను అంచనావేసి, రీడింగ్లకు సరైన సర్దుబాటు తప్పనిసరిగా చేయాలి.

ప్రశ్న 4.
కొలత ఫలితాన్ని అందులో ఉండే దోషాన్ని సూచిస్తూ ఏవిధంగా నివేదిస్తారో (reported) ఉదాహరణలతో వివరించండి.
జవాబు:
ఏదైనా భౌతికరాశిని కొలిచినపుడు, ఆ రాశి యొక్క ప్రామాణిక విలువ (ప్రమాణం)తో పోల్చాలి. ప్రతి ప్రక్రియలో ఉండే దోషాలను పూర్తిగా తొలగించి కొలవడం సాధ్యం కాదు. మనం పూర్తి శ్రద్ధతో కొలిచినప్పటికీ కొలిచిన విలువ ఎల్లప్పుడూ నిజవిలువకు (లేదా) యధార్థ వేరుగా ఉంటుంది.

ప్రశ్న 5.
సార్థక సంఖ్యలంటే ఏవి? ఒక కొలత ఫలితాన్ని నివేదించేటప్పుడు అవి ఏమి సూచిస్తాయి?
జవాబు:
ఒక కొలతను సూచించే సంఖ్యలో నిశ్చయంగా తెలిసిన అంకెలు, వాటికి తోడు అదనంగా అంచనా ప్రకారం చేర్చిన అంకెలు వీటన్నింటినీ కలిపి సార్థక సంఖ్యలు (లేదా) సార్థక అంకెలు అంటారు.
ఉదాహరణ :
లఘులోలకం యొక్క ఆవర్తన కాలం 1.62, దీనిలో 1 మరియు 6 నిశ్చయంగా తెలిసిన అంకెలు, 2 అనునది అంచనా ప్రకారం చేర్చిన అంకె. కాబట్టి కొలిచిన విలువలో మూడు సార్థక సంఖ్యలు కలవు.

ప్రశ్న 6.
ప్రాథమిక ప్రమాణాలు, ఉత్పన్న ప్రమాణాల మధ్య తేడాలు రాయండి.
జవాబు:

1. ప్రాథమిక రాశుల ప్రమాణాలను ప్రాథమిక ప్రమాణాలు అంటారు. ప్రాథమిక ప్రమాణాలను మరొక దానినుండి రాబట్టలేము. వేరొక ప్రమాణాలనుండి రాబట్టలేము.
2. ఉత్పన్న రాశుల ప్రమాణాలను ఉత్పన్న ప్రమాణాలు అంటారు.

ప్రశ్న 7.
ఒకే భౌతికరాశికి వేరువేరు ప్రమాణాలు ఎందుకు ఉంటాయి?
జవాబు:
మనకు వేరు వేరు పద్ధతులు కలవు. అవి C.G.S పద్ధతి, M.S.K పద్ధతి, E.P.S పద్ధతి మరియు S. I పద్ధతి. అందువలన ఒకే భౌతికరాశికి వేరువేరు ప్రమాణాలు కలవు.

ప్రశ్న 8.
మితీయ విశ్లేషణ అంటే ఏమిటి?
జవాబు:
ఉత్పన్న భౌతిక రాశులను, ప్రాథమిక రాశుల ప్రమాణాలలో తెలియజేయుటను మితి విశ్లేషణ అంటారు.

మితివిశ్లేషణ ద్వారా ఇచ్చిన సమీకరణం సరైనదో, కాదో తెలుసుకోవచ్చు. ఒక పద్ధతిలో ప్రమాణాలను వేరొక పద్ధతిలోకి మార్చవచ్చు మరియు వివిధ భౌతిక రాశుల మధ్య సంబంధాన్ని సూచించే సమీకరణాలను రాబట్టవచ్చు.

ప్రశ్న 9.
కేంద్రకం వ్యాసార్ధంతో పోలిస్తే పరమాణు వ్యాసార్ధం పరిమాణ క్రమాలలో (orders of magnitude) ఎంత ఎక్కువగా ఉంటుంది?
జవాబు:
కేంద్రక వ్యాసార్థం పరిమాణం = 10^-14m
పరమాణువు వ్యాసార్థం పరిమాణం = 10^-10m

కాబట్టి కేంద్రకం వ్యాసార్థంతో పోలిస్తే పరమాణు వ్యాసార్థం పరిమాణక్రమాలలో 10^-4 m ఎక్కువ.

ప్రశ్న 10.
ఏకీకృత పరమాణు ద్రవ్యరాశి ప్రమాణాన్ని kg లో వ్యక్తం చేయండి.
జవాబు:
ఏకీకృత పరమాణు ద్రవ్యరాశి ప్రమాణం = \(\frac{1}{12}\) × c¹² – ద్రవ్యరాశి
1 a.m.u = 1.66 × 10^-27 Kg

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఒక పరికరం వెర్నియర్ స్కేలు 50 విభాగాలు కలిగి ఉంది. ఇవి ప్రధాన స్కేలుపై ఉండే 49 విభాగాలతో ఏకీభవిస్తాయి. ప్రధాన స్కేలులోని ప్రతి విభాగం విలువ 0.5mm. అయితే ఈ పరికరంతో కొలిచే దూరంలో కనిష్ఠ యధార్థతారాహిత్యం (inaccuracy) ఎంత ఉంటుంది?
జవాబు:
ప్రధాన స్కేలుపై ప్రతి విభాగం విలువు = 0.5 m.m
వెర్నియర్ స్కేల్పై విభాగాల సంఖ్య = 50
వెర్నియర్ కాలిపర్స్ కనీసపు కొలత = \(\frac{S}{N}\)

కాబట్టి దూరం కొలవడంలో కనిష్ఠ యధార్ధత 0.01 m.m (లేదా)
1 M.S.D విలువ = 0.5 m.m, N = 50
N V.S.D = (N-1) M.S.D
49 M.S.D = 50 V.S.D
1 V.S.D = \(\frac{49}{50}\)M.S.D = \(\frac{49}{50}\) × 0.5 m.m

∴ కనీసపు కొలత = 1 M.S.D – 1 V.S.D = (0.5 – \(\frac{49}{50}\) × 0.5) = (1 – \(\frac{49}{50}\))0.5
= \(\frac{1}{50}\) × 0.5 = 0.01m.m
కాబట్టి దూరం, కొలవడంలో కనిష్ఠ యధార్ధత 0.01 m.m

ప్రశ్న 2.
ప్రమాణాల ఒక వ్యవస్థలో బలానికి ప్రమాణం 100N, పొడవుకు ప్రమాణం 10m, కాలానికి ప్రమాణం 100 s. ఈ వ్యవస్థలో ద్రవ్యరాశికి ఉండే ప్రమాణం ఏది?
జవాబు:
బలం (F) = 100N; పొడవు (L) = 10m; కాలం (T) = 100s
F = ma

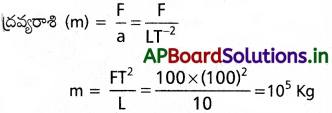
ప్రశ్న 3.
భూమి నుంచి ఒక గెలాక్సీ దూరం 10²⁵ m ల క్రమంలో ఉంది. గెలాక్సీ నుంచి కాంతి మనల్ని చేరేందుకు పట్టే కాలం పరిమాణం క్రమాన్ని గణించండి.
జవాబు:
భూమి నుండి గెలాక్సీ వరకు దూరం = 10²⁵ m
కాంతి వేగం (c) = 3 × 10⁸m/s

ప్రశ్న 4.
భూమి-చంద్రుల మధ్య దూరం సుమారు భూవ్యాసార్థానికి 60 రెట్లు. చంద్రుడి నుంచి చూస్తే భూమి వ్యాసం సుమారుగా ఎంత ఉంటుంది ?
జవాబు:
భూమి, చంద్రుడు మధ్యదూరం
భూమి వ్యాసార్ధం = R
r = 60R = 60 × 640 × 10³ (∵ R = 6400 Km)

l = 11.16 × 10³Km ⇒ వ్యాసం( 1 ) = 11.16 × 10³Km

ప్రశ్న 5.
లోలకం 20 డోలనాలకు పట్టే కాలానికి వచ్చిన మూడు కొలతలు వరుసగా t₁ = 39.6 s, t₂ = 39.9 s, t₃ = 39.5s. కొలతల్లోని ఖచ్చితత్వం ఎంత? కొలతల్లోని యధార్ధత ఎంత?
జవాబు:
డోలనాల సంఖ్య = 20
t₁ = 39.6 Sec, t₂ = 39.9 Sec, t₃ = 39.5 Sec

సగటు విలువ = 39.7 Sec
ఖచ్చితత్వం = 0.1 Sec
కొలిచిన విలువ, నిజవిలువకు దగ్గరగా ఉంటే, అది యధార్థత. కాబట్టి యధార్థత 39.6 s అవుతుంది.

ప్రశ్న 6.
1 కెలోరి = 4.23, 1J = 1kg m²s^-2. ద్రవ్యరాశికి ప్రమాణం a’ kg గా, పొడవుకు ప్రమాణం \(\hat{\mathbf{a}}\)m గా, కాలం ప్రమాణం \(\tilde{\mathrm{a}}\)s గా ఉండే ఒక ప్రమాణ వ్యవస్థను వాడినపుడు, కొత్త వ్యవస్థలో కెలోరికి ఉండే పరిమాణం 4.2 \(\stackrel{\wedge-1}{a} a^{\wedge}-2 \wedge 2\) అని చూపండి.
జవాబు:
1 కెలోరీ = 4.2 J ⇒ 1 J = 1 kg m²s^-2
1 కెలోరీ = 4.2 kg m²s^-2
క్రొత్త పద్ధతిలో, 1 కెలోరీ = 4.2 \(\hat{a} \hat{a}^2 \hat{a}^{-2}\)

ప్రశ్న 7.
శూన్యంలో కాంతి వడి 1 ms2 అయ్యేవిధంగా పొడవుకు ఒక కొత్త ప్రమాణాన్ని ఎంచుకొన్నారు. సూర్యుడి నుంచి కాంతి భూమిని చేరేందుకు పట్టేకాలం 8 నిమిషాల 20 సెకన్లయితే కొత్త ప్రమాణాల్లో సూర్యుడు -భూమి మధ్య దూరం ఎంత?
జవాబు:
శూన్యంలో కాంతి వేగం (V) = 1m/s
పట్టుకాలం (t) = 8 నిముషాల 20 సెకండ్లు= 500 Sec
సూర్యుడు మరియు భూమి మధ్య దూరం (d) = \(\frac{V}{t}\)
d = \(\frac{1}{500}\) = 0.002m

ప్రశ్న 8.
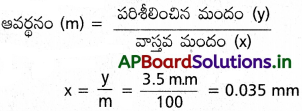
100 ఆవర్ధనం ఉండే సూక్ష్మదర్శినిని ఉపయోగించి ఒక విద్యార్థి మానవుడి వెంట్రుక మందాన్ని కొలుస్తున్నాడు. 20 పరిశీలనల వల్ల వెంట్రుక సగటు మందాన్ని (సూక్ష్మదర్శినిలో చూసినదాని దృష్ట్వా) 3.5mm గా కనుక్కొన్నాడు. అంచనాకు వచ్చే మందం ఎంత ?
జవాబు:
సూక్ష్మదర్శిని ఆవర్ధనం (M) = 100
పరిశీలించిన మందం = 3.5 m.m

ప్రశ్న 9.
కొలవగలిగే నాలుగు రాశులు a, b, c, d లతో X అనే భౌతికరాశి కింది విధంగా సంబంధాన్ని కలిగి ఉంది.
X =a²b³c^5/2d^-2
a,b,c,d లను కొలవడంలో దోషశాతాలు వరుసగా 1%, 2%, 3%,4% అయితే X లో దోషశాతం ఎంత ?
జవాబు:
X =a²b³c^5/2d^-2

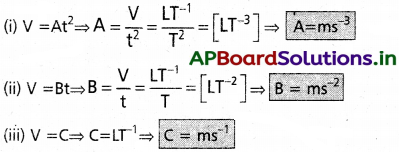
10. ఒక వస్తువు వేగం υ = At² + Bt + C అని ఇవ్వడమైంది. υ, t లను SI ప్రమాణాల్లో వ్యక్తం చేస్తే A,B,C లకు ప్రమాణాలు రాయండి.
జవాబు:
V=At² + Bt + C
సజాతీయత నియమం ప్రకారం

లెక్కలు (Problems)

ప్రశ్న 1.
P= El²m^-5G^-2 అనే సమాసంలో రాశులు E, l, m, G లు వరుసగా శక్తి, కోణీయ ద్రవ్యవేగం, ద్రవ్యరాశి,’ గురుత్వస్థిరాంకాలను సూచిస్తే Pఒక మితిరహిత రాశి అని చూపండి.
సాధన:
P = E L² m G^-2
శక్తి (E) = [ML² T^-2]
కోణీయ ద్రవ్యవేగం (L) = [ML² T^-1]
ద్రవ్యరాశి = [M]
విశ్వగురుత్వ స్థిరాంకం (G) = [M^-1L³ T^-2]
P = [ML² T^-2] [ML² T^-1]² [M]^-5 [M^-1L³T^-2]^-2
P = M^{1 + 2 – 5 + 2} L^{2 + 4 – 6} T^{-2 – 2 + 4}
P = M°L° T°
కాబట్టి P మితిరహితరాశి

ప్రశ్న 2.
కాంతి వేగం c, ప్లాంక్ స్థిరాంకం h, విశ్వ గురుత్వ స్థిరాంకం G లను ప్రాథమిక రాశులుగా తీసుకొంటే, ఈ రాశుల మితుల్లో ద్రవ్యరాశి, పొడవు, కాలాలను రాయండి. [Mar. ’13]
సాధన:
i) M ∝ G^xC^yh^z
[M¹ L° T°] = [M^-1 L³ T^-2]^x [LT^-1]^y [ML²T^-1]^z
[M¹ L° T°] = [M^-x+z L^3x+y+2z T^{-2x – y – z}]
– x + z = 1, 3x + y + 2z = 0, – 2x – y – z = 0
ఈ సమీకరణాలను సాధించగా

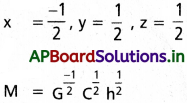
M = \(\sqrt{\frac{hc}{G}}\)

ii) పొడవు (l) ∝ G^xC^yh^z → (1)
[M°L¹T°] = [M^-1 L³ T^-2]^x [LT^-1]^y [ML²T^-1]^z
[M°L¹T°] = M^{– x + z} L^3x+y+2zT^{-2x – y – z}
సజాతీయత నియమం ప్రకారం
– x + z = 0, 3x + y + 2z = 0, – 2x – y – z = 0
ఈ సమీకరణాలను సాధించగా
x = \(\frac{1}{2}\), y = \(\frac{-3}{2}\), z = \(\frac{1}{2}\)

iii) కాలం (T) ∝ G^xC^yh^z
[M°L°T¹] = [M^-1 L³ T^-2]^x [LT^-1]^y [ML² T^-1]^z
[M°L°T¹] = M^{– x + z} L^{3x + y + 2z} T^{– 2x – y – z}
సజాతీయత నియమం ప్రకారం
– x + 2 = 0, 3x + y + 2z = 0, – 2x – y – z = 1
ఈ సమీకరణాలను సాధించగా

ప్రశ్న 3.
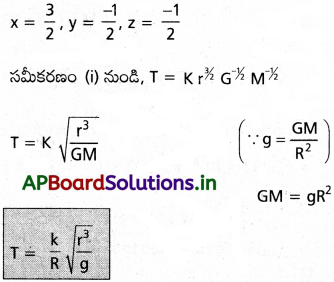
M ద్రవ్యరాశి, R వ్యాసార్ధం కలిగి ఉండే గ్రహం చుట్టూ r వ్యాసార్ధం ఉన్న వృత్తాకార కక్ష్యలో ఒక కృత్రిమ ఉపగ్రహం పరిభ్రమిస్తుంది. మితీయ విశ్లేషణ ఆధారంగా ఉపగ్రహ కక్ష్యావర్తన కాలం T = \(\frac{\hat{e}}{R} \sqrt{\frac{r^3}{g}}\) అని చూపండి. ఇక్కడ \(\hat{\mathbf{e}}\) మితిరహిత స్థిరాంకం, g గురుత్వ త్వరణం.
సాధన:

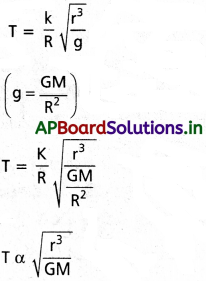
∴ T ∝ r^xG^yM^z
T = kr^xG^yM^z → (1)
[M°L° T¹] = K[L]^x [M^-1L³ T^-2]^y [M]^z
[M°L° T¹] = K[M^{y + z} L^{x + 3y} T^-2y]
−y + z = 0, x + 3y = 0, 1 = −2y
పై సమీకరణాలను సాధించగా

ప్రశ్న 4.
కింది సంఖ్యల్లో సార్ధక సంఖ్యలు ఎన్ని ఉన్నాయో తెలపండి.
a) 6729 b) 0.024 c) 0.08240 d) 6.032 e) 4.57 × 10⁸
సాధన:
a) 6729 – 4 సార్థక సంఖ్యలు
b) 0.024 – 2 సార్థక సంఖ్యలు
c) 0.08240 – 4 సార్థక సంఖ్యలు
d) 6.032 – 4 సార్థక సంఖ్యలు
e) 4.57 × 10⁸ – 3 సార్థక సంఖ్యలు

ప్రశ్న 5.
రెండు కర్రల పొడవులు వరుసగా 12.132 cm, 12.4 cm. ఈ కర్రలను ఒకదాని చివర మరొకదాని చివరకు తాకునట్లు అమర్చితే మొత్తం పొడవు ఎంత? రెండింటిని ఒకదాని పక్క మరొకటి అమర్చితే పొడవుల్లో వ్యత్యాసం ఎంత?
సాధన:
a) కడ్డీల యొక్క పొడవులు
l₁ = 12.132 cm, l₂ = 12.4 cm
ఇక్కడ l₂ కు దశాంశ బిందువు తర్వాత ఒక స్థానం ఉంది. కాబట్టి l₁ ను రెండు దశాంశస్థానాలకు సవరించాలి.
l = l₁ + l₂ = 12.13 + 12.4 = 24.53
కాబట్టి ఫలితాన్ని దశాంశ బిందువు తర్వాత ఒక స్థానానికి సవరించాలి.
∴ తుది ఫలితం = 24.5 cm

b) l₁ = 12.132 cm l₂ = 12.4 cm
ఇక్కడ l₁ ను దశాంశ బిందువు తర్వాత రెండు స్థానాలకు సవరించాలి.
l₂ – l₁ = 12.4 – 12.13 = 0.27
ఇప్పుడు దీనిని దశాంశ బిందువు తర్వాత ఒక స్థానానికి సవరించాలి.
l₂ – l₁ = 0.3

ప్రశ్న 6.
సమ ఘనం భుజం పొడవు 7.203 m. (i) ఘనం ఉపరితల వైశాల్యం, ఘనం ఘనపరిమాణాలను తగిన సార్ధక సంఖ్యలకు లెక్కించండి.
సాధన:
ఘనం యొక్క భుజం (a) = 7.203 m
(i) ఉపరితల వైశాల్యం (A) = 6a²
= 6 × (7.203)² = 311.299
7.203లో సార్ధక సంఖ్యలు నాలుగు (4), ఫలితాన్ని కూడా నాలుగు సార్ధక సంఖ్యలకు సవరించాలి.
∴ (A) = 311.3m²

(ii) ఘనం యొక్క ఘనపరిమాణం = a³
= (7.203)³ = 373.71
ఈ విలువను నాలుగు సార్థక సంఖ్యలకు సవరించాలి.
∴ V = 373.7 m³

ప్రశ్న 7.
ఒక వస్తువు ద్రవ్యరాశి 2.42 g, ఘనపరిమాణం 4.7 cm³. వాటిలోని దోషాలు వరుసగా 0.01 g, 0.1 cm³ అయితే వస్తువు సాంద్రతలో గరిష్ఠ దోషాన్ని కనుక్కోండి.
సాధన:
M = 2.42 g, V = 4.7 cm³
∆Μ = 0.01g, ∆V = 0.1 cm³

ప్రశ్న 8.
గోళం వ్యాసార్ధం కొలవడంలో దోషం 1% అయితే గోళం ఘనపరిమాణం కొలవడంలో దోషం ఎంత?
సాధన:

ప్రశ్న 9.
ద్రవ్యరాశి, వడిలో దోష శాతాలు వరుసగా 2%, 3% అయితే గతిజ శక్తిలో గరిష్ట దోషశాతం ఎంత?
సాధన:

ప్రశ్న 10.
ప్రామాణిక ఉష్ణోగ్రతా పీడనాల వద్ద ఒక మోల్ ఆదర్శవాయువు 22.4L (మోలార్ ఘనపరిమాణం) ఘనపరిమాణం ఆక్రమిస్తుంది. హైడ్రోజన్ అణు పరిమాణం సుమారుగా 1 Å అయితే హైడ్రోజన్ మోలార్ ఘనపరిమాణానికి, పరమాణు ఘన పరిమాణానికి మధ్య నిష్పత్తి ఎంత?
సాధన:
మోలార్ ఘనపరిమాణం = 22.4 లీటర్లు
= 22.4 × 1000 c.c.
= 22.4 × 10^-3 m³
హైడ్రోజన్ అణువు వ్యాసము
= 1A ° 10^-10 m

పరమాణు ఘనపరిమాణం = V × అవగాడ్రో సంఖ్య (N)
= 0.5233 × 10^-30 × 6.023 × 10²³ = 3.151 × 10^-7

అదనపు లెక్కలు (Additional Problems)

ప్రశ్న 1.
ఖాళీలను పూరించండి.
a) 1 cm భుజం పొడవు ఉండే సమఘనం m ఘనపరిమాణం ……….. m³
b) 2.0 cm వ్యాసార్ధం, 10.0 cm ఎత్తు ఉండే ఘన స్తూపం ఉపరితల వైశాల్యం (mm)²
c) 18 km h^-1 వడితో చలిస్తున్న వాహనం 1 s లో ప్రయాణించే దూరం…… m
d) సీసం సాపేక్ష సాంద్రత 11.3 అయితే దాని సాంద్రత …………… g cm³ లేదా …………… kg m^-3
సాధన:
a) పొడవు L = 1 cm = 10^-2 m
ఘనం ఘనపరిమాణం L³ = (10^-2)³
= 10^-6 m³

b) r = 2 cm = 20 m.m
h = 10.0 cm = 100 m.m
ఘనస్థూపం ఉపరితల వైశాల్యం 2πr × h
= 2 × \(\frac{22}{7}\) × 20 × 100
= 1.26 × 10⁴ m.m²

c) వడి (V) = 18 kmph
= \(\frac{18\times1000}{60\times60}\) = 5 m/s
∴ 1 సెకనులో ప్రయాణించిన దూరం = 5 m

d) సాపేక్ష సాంద్రత = 11.3 gm/c.c
= \(\frac{11.3\times10^{3}}{(10^{-2})^3}\)
= 11.3 × 10³ kg/m³

ప్రశ్న 2.
ప్రమాణాలను తగురీతిలో పరివర్తన చేయడం ద్వారా ఖాళీలను పూరించండి.
a) 1 kg m² s^-2 = …. 9 cm² 5^-2
b) 1 m = …. 1y (కాంతి సంవత్సరాలు)
c) 3.0 ms^-2 = …. km h^-2
d) G = 6.67 × 10^-11 N m² (kg)^-2 (cm)³ s^-2 g^-1.
సాధన:
a) 1 kg m² s^-2
= 1 × 10³ × (10²)² s^-2 = 10⁷ gm cm² s^-2

b) 1 కాంతి సంవత్సరం = 9.46 × 10¹⁵ m
∴ 1m = \(\frac{1}{9.46\times10^{-16}}\) కాంతి సంవత్సరం
= 1.053 × 10^-16 కాంతి సంవత్సరం

c) 3ms^-2 = 3 × 10^-3 km(\(\frac{1}{60\times60}\)h)^-2
= 3 × 10^-3 × 3600 × 3600 km h^-2
= 3.888 × 10⁴ km h^-2

d) G = 6.67 × 10^-11 Nm² kg^-2
= 6.67 × 10^-11 (kg ms^-2) m² kg^-2
= 6.67 × 10^-11 m³ s^-2 kg^-1
= 6.67 × 10^-11 (100 cm)³ s^-2 (1000 g)^-1
= 6.67 × 10^-8 cm³ s^-2 g^-1

ప్రశ్న 3.
శక్తి లేదా ఉష్ణానికి ప్రమాణం కెలోరి. దీని విలువ సుమారు 4.2 J ఇక్కడ 1J = 1 kg m²s^-2. ద్రవ్యరాశికి ప్రమాణం a kg, పొడవుకు ప్రమాణం b m, కాలానికి ప్రమాణం g s. అయ్యే ప్రమాణాల వ్యవస్థను వాడినామనుకోండి అప్పుడు కొత్త ప్రమాణాల పదాలలో కెలోరికి ఉండే పరిమాణం 4.2 a^-1b^-2 g² అని చూపండి.
సాధన:
1 కెలోరీ = 4.2 J = 4.2 Kg m²S^-2
ద్రవ్యరాశి క్రొత్త ప్రమాణం a kg
∴ 1 kg = \(\frac{1}{a}\) = a^-1
అదేవిధంగా 1m = b^-1 ద్రవ్యరాశి క్రొత్త ప్రమాణం
1s = g^-1 కాలం క్రొత్త ప్రమాణం
1 కెలోరీ = 4.2 (a^-1) (b^-1)² (g^-1)^-2
1 కెలోరీ = 4.2a^-1 b^-2g², శక్తి యొక్క క్రొత్త ప్రమాణం

ప్రశ్న 4.
కింది ప్రవచనాన్ని (statement) స్పష్టంగా వివరించండి :
” పోలికకు అవసరమయ్యే ప్రామాణికాన్ని నిర్దేశించకుండా మితీయరాశిని పెద్దది లేదా చిన్నది అని పిలవడం అర్థరహితం” దీన్ని దృష్టిలో ఉంచుకొని కింది ప్రవచనాలను అవసరమైన చోట సరిచేసి తిరిగి రాయండి.
a) పరమాణువులు అతిచిన్న వస్తువులు.
b) జెట్ విమానం ఎక్కువ వడితో చలిస్తుంది.
c) బృహస్పతి ద్రవ్యరాశి చాలా ఎక్కువ.
d) ఈ గదిలోని గాలి అధిక సంఖ్యలో అణువులను కలిగి ఉంది.
e) ఎలక్ట్రాన్ కంటే ప్రోటాన్ ద్రవ్యరాశి చాలా ఎక్కువ.
f) కాంతి వేగం కంటే ధ్వని వేగం చాలా తక్కువ.
సాధన:
i) పై నిర్వచనం సరియైనది. మితిరహితరాశులను కొన్ని ప్రమాణాలకు లోబడి పెద్దవా (లేదా) చిన్నవా అని పోల్చుతారు.
ఉదా : కోణం మితిరహితరాశి, ∠θ = 60° అనునది ∠θ = 30° కన్నా ఎక్కువ కాని ∠θ = 90° కన్నా తక్కువ.

ii) a) పరమాణువు పరిమాణం, ఒక గుండు సూదిమొన కన్నా చాలా చిన్నది.
b) సూపర్ ఫాస్ట్ రైలు కన్నా జెట్ విమానం చాలా వేగంగా పోతుంది.
c) భూమి ద్రవ్యరాశి కన్నా అంగారకుడి ద్రవ్యరాశి బాగా ఎక్కువ.
d) ఒక మోల్ వాయువులోని అణువుల కన్నా, గదిలో
గాలిలో అణువుల సంఖ్య ఎక్కువ.
e) పై స్టేట్మెంట్ సరియైనది.
f) పై స్టేట్మెంట్ సరియైనది.

ప్రశ్న 5.
శూన్యంలో కాంతి వడి 1ms^-2 అయ్యేవిధంగా పొడవుకు ఒక కొత్త ప్రమాణాన్ని ఎంచుకొన్నారు. సూర్యుడి నుంచి కాంతి భూమిని చేరేందుకు పట్టేకాలం 8 నిమిషాల 20 సెకన్లయితే కొత్త ప్రమాణాల్లో సూర్యుడు-భూమి మధ్య దూరం ఎంత?
సాధన:
శూన్యంలో కాంతివేగం c = 1 పొడవు క్రొత్త ప్రమాణం s^-1
కాంతి సూర్యుడి నుండి భూమిని చేరుటకు పట్టుకాలం
t = 8 నిమిషాల 20 సెకండ్లు = 8 × 60 + 20
= 500 సెకండ్ల
భూమి, సూర్యుడి మధ్యదూరం (x) = C × t
∴ పొడవు క్రొత్త ప్రమాణం s^-1 × 500
= 500 పొడవు క్రొత్త ప్రమాణం

ప్రశ్న 6.
పొడవును కొలవడానికి కింది వాటిలో ఏది చాలా ఖచ్చితమైన పరికరం?
a) కదిలే స్కేలుపై 20 వెర్నియర్ విభాగాలు ఉండే వెర్నియర్ కాలిపర్స్
b) 1 mm పిచ్, 100 తలస్కేలు విభాగాలు ఉండే స్కూృగేజి.
c) కాంతి తరంగదైర్ఘ్యవిలువకు తక్కువ/సమానం వరకు పొడవును కొలిచే దృక్ సాధనం.
సాధన:
a) వెర్నియర్ కాలిపర్స్ కనీసపు కొలత

b) స్క్రూగేజి కనీసపు కొలత

c) కాంతి సంవత్సరం
λ = 10^-5 cm = 0.00001 cm
ఎక్కువ యదార్థ కలది దృశావస్తువు

ప్రశ్న 7.
100 ఆవర్ధనం ఉండే సూక్ష్మదర్శిని ఉపయోగించి ఒక విద్యార్థి మానవుడి వెంట్రుక మందాన్ని కొలుస్తున్నాడు. 20 పరిశీలనల వల్ల వెంట్రుక సగటు మందాన్ని (సూక్ష్మదర్శినిలో చూసినదాని దృష్ట్యా) 3.5 mm.గా కనుక్కొన్నాడు. అంచనాకు వచ్చే మందం ఎంత
సాధన:

ప్రశ్న 8.
కింది వాటికి సమాధానం రాయండి:
a) నీకు ఒక దారం, మీటరు స్కేలును ఇస్తే దారం వ్యాసాన్ని ఏవిధంగా అంచనా వేస్తావు?
b) ఒక స్కూృగేజి పిచ్ 1.0 mm, వృత్తాకార స్కేలుపై విభాగాలు 200. వృత్తాకార స్కేలుపై విభాగాల సంఖ్యను అనియతంగా పెంచడం ద్వారా స్కూృగేజి యధార్ధతను పెంచడం సాధ్యమని నీవు అనుకొంటున్నావా?
c) వెర్నియర్ కాలిపర్స్ సహాయంతో పలుచని ఇత్తడి కడ్డీ సగటు వ్యాసాన్ని నిర్ణయించవలసి ఉంది. 5 కొలతల సమితి కంటే 100 కొలతల సమితితో వచ్చే అంచనా విలువ ఎక్కువ నమ్మదగినదని మనమెందుకు ఆశిస్తాం?
సాధన:
a) ద్వారం వ్యాసం చాలా చిన్నది కాబట్టి దానిని మీటరు స్కేలు ఉపయోగించి కొలవలేము. మీటరు స్కేలుపై దారాన్ని అనేకచుట్లుగా చుట్టాలి. ఆ చుట్లు బాగా దగ్గర దగ్గరగా చుట్టాలి.
n చుట్లు గల దారం పొడవు l
∴ దారం వ్యాసం = \(\frac{1}{n}\)

b) కనీసపు కొలత

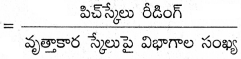
వృత్తాకార స్కేలుపై విభాగాల సంఖ్య పెరిగితే, కనీసపు కొలత తగ్గుతుంది. కాబట్టి ఖచ్చితత్వం పెరుగు తుంది. కాని ప్రాయోగికంగా సాధారణ మానవుని కంటితో రీడింగ్లను ఖచ్చితంగా కొలవలేము.

c) తక్కువ పరిశీలనలు (5) కన్నా ఎక్కువ పరిశీలనలు (100) ఆధారపడదగినవిగా ఉంటాయి. దీనికి కారణం ధనయాదృచ్ఛిక దోషం, రుణయాదృచ్ఛిక దోషం ఒకే పరిమాణంలో ఉంటాయి. కాబట్టి పరిశీలనల సంఖ్య పెరిగే కొద్దీ యాదృచ్ఛిక దోషాలు తగ్గి, విలువలు ఆధారపడదగినవిగా ఉంటాయి.

ప్రశ్న 9.
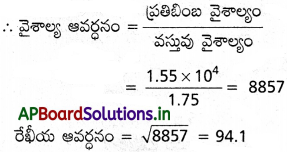
35 mm స్లైడుపై ఒక ఇంటి ఛాయాచిత్రం వైశాల్యం 1.75 cm². ఆ స్లెడును తెరపై ప్రొజెక్ట్ చేసినపుడు ఇంటి వైశాల్యం 1.55 m² గా ఉంది. ప్రొజెక్టర్-తెర అమరిక రేఖీయ ఆవర్ధనం ఎంత?
సాధన:
వస్తువు వైశాల్యం = 1.75 cm²
ప్రతిబింబం వైశాల్యం = 1.55 m² = 1.55 × 10⁴cm²

ప్రశ్న 10.
కింద ఇచ్చిన వాటిలో సార్ధక సంఖ్యలు ఎన్ని ఉన్నాయి?
a) 0.007 m², b) 2.64 ×10²⁴ kg, c) 0.2370 g cm^-3, d) 6.320 J, e) 6.032 N m^-2, f) 0.0006032 m²
సాధన:
ఇచ్చిన సంఖ్యలకు ఈ క్రింది సార్ధక సంఖ్యలు కలవు.
a) ఒకటి b) మూడు c) నాలుగు d) నాలుగు e) నాలుగు f) నాలుగు.

ప్రశ్న 11.
దీర్ఘచతురస్రాకార లోహ పలక పొడవు, వెడల్పు, మందాలు వరుసగా 4.234m, 1.005 m, 2.01 cm లు సరయిన సార్ధక సంఖ్యల వరకు ఆ పలక వైశాల్యం, ఘనపరిమాణాలను రాయండి. సాధన:
ఇక్కడ పొడవు l = 4.234 m
వెడల్పు b = 1.005 m
మందం t = 2.01 cm = 2.01 × 10^-2 m
పలక వైశాల్యం = 2 (l × b + b × t + t × l)
= 2(4.234 × 1.005 + 1.005 × 0.0201 + 0.021 × 4.234)
=2(4.3604739)
= 8.7209478 m²

వైశాల్యం మూడు సార్ధక సంఖ్యలు కలిగి ఉండాలి. కావున వీటిని సవరించాలి.
వైశాల్యం = 8.72 m²
ఘనపరిమాణం (V) = l × b × t
V = 4.234 × 1.005 × 0.0201
= 0.0855289
= 0.855 m³
దీనిలో మూడు సార్ధక సంఖ్యలు కలవు.

ప్రశ్న 12.
ఒక పెట్టెను కిరాణా షాపుదారు వాడే త్రాసుతో తూస్తే వచ్చిన ద్రవ్యరాశి 2.300 kg. ఇప్పుడు ఈ పెట్టెకు 20.15 g, 20.17 g ద్రవ్యరాశులు గల రెండు బంగారు ముక్కలను కలిపారు. (a) పెట్టె మొత్తం ద్రవ్యరాశి, (b) ముక్కల ద్రవ్యరాశుల్లో వ్యత్యాసాన్ని సరయిన సార్ధక సంఖ్యల వరకు రాయండి.
సాధన:
పెట్టె ద్రవ్యరాశి m = 2.3 kg
ఒక బంగారం ముక్క ద్రవ్యరాశి
m₁ = 20.15 g = 0.02015 kg
మిగిలిన బంగారం ద్రవ్యరాశి
m₂ = 20.17g = 0.02017 kg

a) మొత్తం ద్రవ్యరాశి = m + m₁ + m₂
= 2.3 +0.02015 +0.02017
= 2.34032 kg
ఫలితాన్ని దశాంశ స్థానం తర్వాత ఒక సంఖ్యకు సవరించాలి.
మొత్తం ద్రవ్యరాశి = 2.3 kg

b) ద్రవ్యరాశులలో తేడా
= m₂ – m₁ = 20.17 – 20.15
= 0.02gm

ప్రశ్న 13.
P అనే భౌతికరాశి a, b, c, d అనే నాలుగు పరిశీలించగలిగే రాశులతో కిందివిధమైన సంబంధాన్ని కలిగి ఉంది :
P = a³b²/(√cd)
a,b,c,d లకొలతల్లోని దోషశాతాలు వరుసగా 1%, 3%, 4%, 2% అయితే P లోని దోషశాతం ఎంత ? పై సంబంధం ఉపయోగించి లెక్కించిన P విలువ 3.763 అయితే, ఫలితాన్ని నీవు ఏ విలువ వరకు సవరిస్తావు ?
సాధన:
ఇక్కడ P = \(\frac{a^3 b^2}{\sqrt{c} d}\)

ఫలితం Pలో రెండు సార్ధక సంఖ్యలు కలవు కాబట్టి 3.763ని సవరిస్తే 3.8 అవుతుంది.

ప్రశ్న 14.
ముద్రణా దోషాలు అనేకంగా ఉండే పుస్తకంలో ఒక నిర్దిష్ట ఆవర్తన చలనం చేస్తున్న కణం స్థానభ్రంశానికి నాలుగు భిన్న ఫార్ములాలు ఉన్నాయి. అవి
a) y = a sin 2 p t/T, b) y = a sin vt, c) y = (a/T) sin t/a, d) y = (a√2) (sin 2 πt /T + cos 2 πt /T)
(a = కణం పొందే గరిష్ఠ స్థానభ్రంశం, v = కణం వడి, T = ఆవర్తన కాలం) మితుల దృష్ట్యా తప్పు అయిన ఫార్ములాలను కొట్టి వేయండి.
సాధన:
త్రికోణమితి ప్రమేయం మితిరహితరాశి అనగా కోణం మితిరహిత రాశి

కాబట్టి (ii) మరియు (iii) సూత్రాలు తప్పు.

ప్రశ్న 15.
భౌతికశాస్త్రంలో ఒక ప్రసిద్ధమైన సంబంధం కణ ‘విరామ ద్రవ్యరాశి’ m₀, చలిస్తున్నప్పుడు ద్రవ్యరాశి m లను కణ వడి v కాంతి వడి c పదాలతో కలుపుతుంది. (ఈ సంబంధం ఆల్బర్ట్ ఐన్స్టీన్ ప్రతిపాదించిన ప్రత్యేక సాపేక్షతా సిద్ధాంతం పర్యవసానంగా మొట్టమొదట వెలువడింది) ఒక బాలుడు ఈ సంబంధాన్ని దాదాపు సరిగానే జ్ఞప్తికి తెచ్చుకొన్నాడు కానీ స్థిరాంకం c ని ఎక్కడ ఉంచాలో మరచిపోయి కింది విధంగా రాశాడు.
m = \(\frac{m_0}{\left(1-v^2\right)^{1 / 2}}\)
ఇందులో కనిపించకుండా పోయిన ఁని ఎక్కడ ఉంచాలో ఊహించండి.
సాధన:
సజాతీయత సూత్రం ప్రకారం, MLT యొక్క ఘాతాలు
ఇరువైపులా సమానం. R.H.S వైపు లవంలో (1 – v²)^1/2

ప్రశ్న 16.
పరమాణు మానంపై (atomic scale) అనువుగా ఉండే పొడవు ప్రమాణం ఆంగ్జామ్, దీన్ని AC తో సూచిస్తారు. 14° = 10^-10 m. హైడ్రోజన్ పరమాణు పరిమాణం సుమారు 0.5A° . ఒక మోల్ హైడ్రోజన్ పరమాణువుల మొత&ం పరమాణు ఘనపరిమాణం m³ ల్లో ఎంత ఉంటుంది?
సాధన:
ఇక్కడ r = 0.5 A° = 0.5 × 10^-10 m
ప్రతి హైడ్రోజన్ పరమాణువు ఘనపరిమాణం = \(\frac{4}{3}\)πr³
\(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³ = 5.236 × 10^-31 3 m³
ఒక గ్రామ్ మోల్ హైడ్రోజన్ పరమాణువుల సంఖ్య అవగాడ్రో సంఖ్య = 6.023 × 10²³

ఒక గ్రామ్ – మోల్ హైడ్రోజన్ పరమాణువు ఘన పరిమాణం
= 5.236 × 10^-31 × 6.023 × 10²³
= 3.154 × 10^-7 m³

ప్రశ్న 17.
ప్రామాణిక ఉష్ణోగ్రతా పీడనాల వద్ద ఒక మోల్ ఆదర్శవాయువు 22.4L (మోలార్ ఘనపరిమాణం) ఆక్రమిస్తుంది. హైడ్రోజన్ అణు పరిమాణం సుమారుగా 1A° అయితే హైడ్రోజన్ మోలార్ ఘనపరిమాణానికి, పరమాణు ఘనపరిమాణానికి మధ్య నిష్పత్తి ఎంత? ఈ నిష్పత్తి అంత పెద్దదిగా ఎందుకు ఉంది?
సాధన:

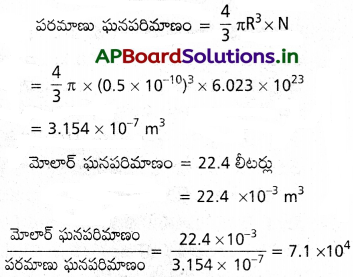
ఈ నిష్పత్తి పరమాణువుల అంతర దూరాల కన్నా అధికం.

ప్రశ్న 18.
సాధారణంగా మనం పరిశీలించే ఈ అంశాన్ని స్పష్టంగా వివరించండి. వేగంగా ప్రయాణిస్తున్న రైలు కిటికీలో నుంచి బయటికి నీవు చూస్తే, దగ్గరలో ఉండే చెట్లు, ఇళ్ళు మొదలైనవి రైలు ప్రయాణ దిశకు వ్యతిరేక దిశలో వేగంగా కదులుతున్నట్లుగా అగుపిస్తాయి. కానీ, దూరంగా ఉండే వస్తువులు (కొండ శిఖరాలు, చంద్రుడు నక్షత్రాలు మొదలైనవి) స్థిరంగా ఉన్నట్లుగా అగుపిస్తాయి. (నిజానికి, నీవు చలిస్తున్నావని నీకు తెలుసు కాబట్టి ఈ దూర వస్తువులు నీతోపాటే చలిస్తున్నట్లు అనిపిస్తుంది)
సాధన:
వస్తువుకు, నేత్రానికి గీసే సరళరేఖను దృష్టిరేఖ అంటారు. రైలు వేగంగా కదిలితే, దగ్గరలో ఉన్న చెట్లపై దృష్టిరేఖ మారును. అందుకని చెట్లు వెనక్కి పోవుచున్నట్లు కనిపిస్తుంది.

దూరపు వస్తువులపై (కొండలు, చంద్రుడు, నక్షత్రాలు) దృష్టిరేఖ మారదు. కాబట్టివాటి దిశ మారదు. అందువలన పర్వతాలు, చంద్రుడు, నక్షత్రాలు వంటి దూరంగా ఉన్నవి నిశ్చలంగా ఉంటాయి.

ప్రశ్న 19.
విభాగం 2.3.1 లో చర్చించిన దృష్టి విక్షేప సూత్రం సుదూరంగా ఉండే నక్షత్రాల దూరాలను నిర్ణయించడానికి ఉపయోగించాం. 6 నెలల ఎడంలో సూర్యుడి చుట్టూ ఉండే దాని కక్ష్యలో గల భూమి రెండు స్థానాలను కలిపే రేఖ ఆధారరేఖ (baseline) AB. అంటే ఆధారరేఖ సుమారు భూకక్ష్య వ్యాసానికి సమానం (≈3 × 10¹¹ m). అయితే మనకు దగ్గర్లో ఉండే నక్షత్రాలు కూడా ఎంత దూరంలో ఉంటాయంటే అంతటి పొడవైన ఆధారరేఖతో అవి కలగచేసే ‘దృష్టి విక్షేపం’ చాపంలో 1″ (సెకను) క్రమంలో మాత్రమే ఉంటుంది. ఖగోళదూరాలకు ‘పార్సెక్’ అనేది అనుకూలమైన ‘పొడవు ప్రమాణం’. ఇది భూమి నుంచి సూర్యుడి వరకు గల దూరానికి సమానంగా ఉండే ఆధారరేఖ యొక్క రెండు వ్యతిరేక చివరలతో చాపపు 1″ (సెకను) పారలాక్స్ (కోణం) (దృష్టి విక్షేపం) ను చూపగలిగే వస్తువు దూరం. ఒక పార్సెక్ విలువ మీటర్లలో ఎంత?
సాధన:
ఆధారరేఖ పొడవు = భూమి నుండి సూర్యుడి వరకు పొడవు
= 1 A.U = 1.5 × 10¹¹m
దృష్టికోణం θ = 1¹¹

కాబట్టి 1 పార్సెక్ 3.1 × 10¹⁶ m

ప్రశ్న 20.
మన సౌరవ్యవస్థకు అత్యంత సమీపంలో ఉండే నక్షత్రం దూరం 4.29 కాంతి సంవత్సరాలు. ఈ దూరం ‘పార్సెక్’ లలో ఎంత? ఆల్పాసెంటారీ (Alpha Centauri) అని పిలువబడే నక్షత్రం సూర్యుని చుట్టూ ఉండే కక్ష్యలో భూమి 6 నెలల ఎడంలో ఉన్నప్పుడు ఉండే రెండు స్థానాల నుంచి చూసినప్పుడు ఎంత దృష్టి విక్షేపాన్ని కలగచేస్తుంది?
సాధన:
x = 4.29 కాంతి సంవత్సరాలు
= 4.29 × 9.46 × 10¹⁵ m

= 1.512 సెకన్లు

ప్రశ్న 21.
విజ్ఞానశాస్త్రానికి భౌతికరాశుల కచ్చిత కొలతలు ఆవశ్యం. ఉదాహరణకు ఒక విమాన వడిని నిశ్చయంగా తెలుసుకోవాలంటే స్వల్ప కాల వ్యవధుల ఎడంలో విడిపోయి ఉన్న దాని స్థానాలను కనుక్కోవడానికి ఒక యధార్థ పద్ధతి మనకు ఉండాలి. రెండో ప్రపంచ యుద్ధంలో రాడారును ఆవిష్కరించడం వెనుక ఉన్న నిజమైన ఉద్దేశం ఇదే. ఆధునిక విజ్ఞానశాస్త్రంలో ఎక్కడైతే పొడవు, కాలం, ద్రవ్యరాశి మొదలైనవాటి కచ్చిత కొలతలు అవసరమవుతాయో అలాంటి భిన్న ఉదాహరణల గురించి ఆలోచించండి. దాంతో పాటు అక్కడ అవసరమయ్యే కచ్చితత్వం పరిమాణాత్మక భావనను ఇవ్వగలిగిన చోట ఇవ్వండి.
సాధన:
సైన్స్ మరియు భౌతికశాస్త్ర నియమాలు అభివృద్ధి చెందాలంటే పొడవు, ద్రవ్యరాశి మరియు కాలాలను ఖచ్చితంగా కొలవాలి.

ఉదాహరణకు లేసర్ కిరణంతో భూమి నుండి, చంద్రుడు వరకు దూరాన్ని కొలిచామనుకోండి. అందుకు కాలంను ఖచ్చితంగా కొలవాలి. అదేవిధంగా దూరం, విమాన వేగాన్ని రాడార్తో కొలవడం మొదలగువాటికి కాలంను ఖచ్చితంగా కొలవాలి. నక్షత్రాల మధ్య దూరాలను కొలుచుటకు దృష్టికోణంను ఖచ్చితంగా కొలవాలి.

స్ఫటికాలలో పరమాణువులలో అంతర దూరాలు ఖచ్చితంగా కొలవాలి. ద్రవ్యరాశి స్పెక్ట్రోమీటరు ఉపయోగించి పరమాణువుల ద్రవ్యరాశిని ఖచ్చితంగా కొలవవచ్చు.

ప్రశ్న 22.
మూల భావనలను, సాధారణ పరిశీలనలను ఉపయోగిస్తూ, రాశులకు ఉజ్జాయింపు అంచనాలను కట్టగలగడం కూడా అంతే ముఖ్యం. ఈ కింది వాటిని అంచనావేసే మార్గాలను ఆలోచించండి. (ఎక్కడైతే అంచనా పొందడం కష్టమో, అక్కడ రాశి యొక్క విలువలో పైహద్దు (upper bound) ను పొందడానికి ప్రయత్నించండి)
a) రుతుపవనాల కాలంలో భారతదేశంపై ఆవరించి ఉండే వర్షాన్ని తీసుకొని రాగలిగే మేఘాల మొత్తం ద్రవ్యరాశి.
b) ఏనుగు ద్రవ్యరాశి
c) తుఫాన్ సమయంలో పవన వడి
d) నీ తలపై ఉండే వెంట్రుకల సంఖ్య
e) మీ తరగతి గదిలోని గాలి అణువుల సంఖ్య.
సాధన:
a) రుతుపవనాల కాలంలో, మెటీరియాలజిస్ట్ 100 cm వర్షపాతం కురిసినట్లుగా నమోదు చేశాడు.
= 100 cm = 1m.
దేశం వైశాల్యం,
A = 3.3 మిలియన్ × km²
= 3.3 × 10⁶ (10³)²
= 3.3 × 10¹² m²
వర్షపు నీరు ఘనపరిమాణం
v = Axh = 3.3 × 10¹² × 1m³
నీటిసాంద్రత ρ = 10 km/m³
వాన నీటి ద్రవ్యరాశి
= vρ = 3.3 × 10¹² × 10³
= 3.3 × 10¹⁵ kg
ఇది భారతదేశం అంతటా కురిసిన వర్షం మొత్తం ద్రవ్యరాశి.

b) ఏనుగు ద్రవ్యరాశి కొలవాలంటే, వైశాల్యం (A) తెలిసిన పడవను తీసుకోవాలి. నీటిలో పడవ లోతును తెలుసుకోవాలి. అది x₁ అనుకొనుము. పడవ వలన స్థానభ్రంశం చెందిన నీటి ఘన పరిమాణం V₁ = Ax₁. ఇప్పుడు పడవలోకి ఏనుగును ఎక్కించాలి. పడవ నీటిలోకి దిగుతుంది. ఇప్పుడు పడవ నీటిలోకి ఎంత లోతు ఉన్నది కొలవాలి. అది x₂ గా తీసుకోవాలి.

పడవ మరియు ఏనుగు వలన స్థానభ్రంశం చెందిన నీటి యొక్క ఘనపరిమాణం V₂ = Ax₂

ఏనుగువల్ల స్థానభ్రంశం చెందిన నీటి ఘన పరిమాణం (V) = V₂ – V₁ = A(x₂ – x₁)

నీటిసాంద్రత p, అయిన ఏనుగు ద్రవ్యరాశి
= తొలగిన నీటి ద్రవ్యరాశి
= Vρ = A(x₂ – x₁)ρ

c) బెలూన్లో వాయువును నింపి గాలి వేగాన్ని తుఫాన్ సమయంలో కొలవవచ్చు. OA అనునది సాధారణ స్థితిలో వాయుబెలూన్ ఉంది. గాలి కుడివైపుకు వీస్తే ఒక సెకన్లో B వద్దకు బెలూన్ చేరినది. అప్పుడు ∠AOB = θను కొలవాలి. బెలూన్ ఎత్తు h అయిన AB = d = hθ. ఇది బెలూన్ ఒక సెకనులో ప్రయాణించిన దూరం. ఇదే గాలివేగం.

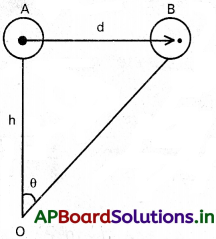
d) ముందుగా తల వైశాల్యాన్ని కొలవాలి. అది A అనుకొనుము. స్క్రూగేజిని ఉపయోగించి, వెంట్రుక మందాన్ని కొలవాలి (d).
వెంట్రుక అడ్డుకోత వైశాల్యం = πd²
తలపై ఉన్న వెంట్రుకల సంఖ్య

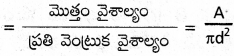
కాబట్టి లెక్కల ప్రకారం తలపై సుమారుగా ఒక మిలియన్ వెంట్రుకలు ఉంటాయి.

e) ముందుగా గది ఘనపరిమాణంను కొలవాలి. N.T.P వద్ద ఒక మోల్ వాయువు ఘనపరిమాణం 22.4 లీటర్లు అనగా 22.4 × 10³ m³
∴ వాయు అణువుల సంఖ్య
= 22.4 × 10^-3 m³ = 6.023 × 10²³
V ఘనపరిమాణం గల తరగతి గదిలో వాయు
అణువుల సంఖ్య = \(\frac{6.023 \times 10^{23}}{22.4 \times 10^{-3}} \times v\)

ప్రశ్న 23.
అతి వేడిగా ఉండే ప్లాస్మా (అయనీకృత పదార్థం) స్థితిలో సూర్యుడు ఉంటాడు. సూర్యుడి అంతర్భాగ ఉష్ణోగ్రత 10⁷ K కు మించి ఉంటుంది. బాహ్య ఉపరితల ఉష్ణోగ్రత సుమారు 6000 K. ఇంతటి అధిక ఉష్ణోగ్రతల వద్ద ఏ పదార్థం కూడా ఘన లేదా ద్రవ ప్రావస్థలో ఉండదు. ఘనపదార్థాలకు, ద్రవాలకు లేదా వాయువులకు ఉండే సాంద్రత వ్యాప్తిలో సూర్యుని ద్రవ్యరాశి సాంద్రత ఏ వ్యాప్తిలో ఉంటుందని లేదా ఉండవచ్చని మీరు భావిస్తున్నారు. మీరు ఊహించిన విలువ సరియైందో కాదో కింది దత్తాంశంతో సరిచూడండి. సూర్యుని ద్రవ్యరాశి : 2.0 × 10³⁰ kg, సూర్యుని వ్యాసార్ధం = 7.0 × 10⁸ m.
సాధన:
m = 2.0 × 10³⁰ kg, R = 7.0 × 10⁸

ఇది ఘన మరియు ద్రవాల సాంద్రత. వాయువులకు కాదు. సూర్యుడిపై బాహ్యపొరలపై లోపలివైపుకు గురుత్వాకర్షణ బలాలు ఉండుటచే సూర్యుడిలో అధిక సాంద్రత ఉంటుంది.

ప్రశ్న 24.
బృహస్పతి గ్రహం భూమి నుంచి 824.7 మిలియన్ కిలోమీటర్ల దూరంలో ఉన్నప్పుడు కోణీయ వ్యాసాన్ని కొలిస్తే 35.72″, గా వచ్చింది. బృహస్పతి వ్యాసాన్ని లెక్కించండి.
సాధన:
ఇక్కడ r = 824.7 × 10⁶ km,
θ = 35.72

ప్రశ్న 25.
వర్షంలో వడితో వడివడిగా నడిచే వ్యక్తి తన గొడుగును నిలువు (క్షితిజ లంబం) తో q కోణం చేసే విధంగా ముందుకు వంచాలి. q, υ ల మధ్య సంబంధాన్ని ఒక విద్యార్థి tan q = υ గా ఉత్పాదించి ఈ సంబంధం సరియైన అవధి కలిగి ఉందని సరిచూశాడు. ఈ అవధి ఆశించినట్లుగానే ఉందని కనుక్కొంటాడు. అవధులు υ > 0, q > 0 (ఎలాంటి ప్రబలమైన గాలి వీచడం లేదని వర్షం నిశ్చలంగా ఉండే వ్యక్తి దృష్ట్యా నిలువుగానే పడుతుందని మనం భావించుకుంటున్నాం) ఈ సంబంధం సరియైందేనని మీరు భావిస్తున్నారా ? కాకపోయి నట్లయితే, సరియైన సంబంధాన్ని ఊహించండి.
సాధన:
tan θ = υ,
υ → 0; θ → 0.
R.H.S = tan θ = [M°L°T°] మరియు
L.H.S = υ = [M° L¹T^-1]
మితులపరంగా ఈ సంబంధం సరియైనది కాదు. సరియైన సంబంధం
tan θ = \(\frac{v^2}{\mathrm{rg}}\)

ప్రశ్న 26.
రెండు సీజియం గడియారాలను నిరాటంకంగా 100 సంవత్సరాలు నడిపిస్తే, వాటి కాలాల్లో వచ్చే మార్పు కేవలం 0.025 అని నొక్కిచెప్పారు. 1 s కాలవ్యవధిని కొలవడంలో ప్రామాణిక సీజియం గడియారం యదార్థతకు ఇది ఏ అర్ధాన్ని ఇస్తుంది?
సాధన:
100 సంవత్సరాలకు దోషం = 0.02s
1 సెకనులో దోషం

కాబట్టి ప్రామాణిక సీజియమ్ గడియారంలో కొలచే కాలం వ్యవధి 1 సెకనుకు యదార్థత 10^-12 s.

ప్రశ్న 27.
సోడియం పరమాణువు పరిమాణాన్ని 2.5 A° గా పరిగణిస్తూ, సోడియం పరమాణువు సగటు ద్రవ్యరాశి సాంద్రతను అంచనా వేయండి. (అవొగాడ్రో) సంఖ్య, సోడియం పరమాణు ద్రవ్యరాశులకు తెలిసిన విలువలను ఉపయోగించండి.) ఈ సాంద్రత విలువను స్ఫటిక ప్రావస్థలోని సోడియం సాంద్రత విలువ 970 kg m^-3 తో పోల్చండి. ఈ రెండు సాంద్రతలు ఒకే పరిమాణ క్రమాన్ని కలిగి ఉన్నాయా? ఉంటే, ఎందుకు?
సాధన:
పరమాణు ఘనపరిమాణం = \(\frac{4}{3}\) πR³ × N
= \(\frac{4}{3}\times\frac{22}{7}\) (1.25 × 10^-10)³ × 6.023 × 10²³ m³
4.93 × 10^-6 m³
సగటు ద్రవ్యరాశి సాంద్రత

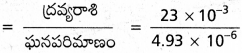
= 4.67 × 103 kg/m³
ఈ రెండు సాంద్రతలు ఒకే క్రమంలో లేవు. ఇది స్ఫటికాలలో పరమాణువుల అంతర దూరాల దశను తెలుపును.

ప్రశ్న 28.
కేంద్రక మానం (nuclear scale) లో అనుకూలమైన పొడవు ప్రమాణం ఫెర్మీ. 1f = 10^-15 m. కేంద్రక పరిమాణాలు ఉజ్జాయింపుగా అనుసరించే అనుభవిక సంబంధం : r = r_oA^1/3
ఇక్కడ r కేంద్రక వ్యాసార్ధం, దాని ద్రవ్యరాశి, సంఖ్య r_o అనేది 1.2 f కు దాదాపు సమానమైన స్థిరాంకం. ఈ నియమం ఆధారంగా భిన్న కేంద్రకాలకు ద్రవ్యరాశి సాంద్రత దాదాపు స్థిరాంకం అని చూపండి. సోడియం కేంద్రకం ద్రవ్యరాశి సాంద్రతను అంచనా వేయండి. ఈ విలువలను అభ్యాసం 27లో పొందిన సోడియం పరమాణు సగటు ద్రవ్యరాశి సాంద్రతతో పోల్చండి.
సాధన:
కేంద్రకం సగటు ద్రవ్యరాశి = m
కేంద్రకంలో న్యూక్లియాన్ల సంఖ్య = n
కేంద్రకం యొక్క ద్రవ్యరాశి M = mA
కేంద్రకం వ్యాసార్థం r = r_oA^1/3

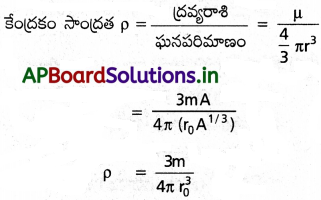
m, r_o లు స్థిరాంకాలు. అన్ని కేంద్రకాల సాంద్రత స్థిరం
m = 1.66 × 10^-27 kg మరియు
r_o = 1.2f = 1.2 × 10^-15 m

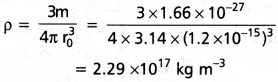
అన్ని కేంద్రకాలకు p స్థిరం కనుక, ఇది సోడియం కేంద్రకం సాంద్రత కూడా అవుతుంది.
సోడియం కేంద్రకం సాంద్రత

ప్రశ్న 29.
లేజర్ (LASER) చాలా తీవ్రత కలిగిన, ఏకవర్ణక, ఏకదిశాత్మక కాంతి పుంజ జనకం. ఈ ధర్మాల ఆధారంగా సుదూరాలను కొలవడానికి లేజర్ను వినియోగించుకోవచ్చు. లేజర్ను ఒక కాంతి జనకంగా ఉపయోగించి భూమి నుంచి చంద్రుని దూరాన్ని చాలా ఖచ్చితంగా ఇదివరకే నిర్ణయించారు. చంద్రుడిపైకి కేంద్రీకరించిన ఒక లేజర్ కాంతి పుంజం చంద్రుని ఉపరితలం నుంచి పరావర్తనం చెంది భూమిని చేరడానికి 2.56s తీసుకొంటుంది. భూమి చుట్టూ పరిభ్రమించే చంద్రుడి కక్ష్యా వ్యాసార్ధం ఎంత?
సాధన:
ఇక్కడ t = 2.56sec
శూన్యంలో లేసర్ కాంతి వేగం = 3 × 10⁸ m/s
లూనార్ కక్ష్యా వ్యాసార్థం, చంద్రుడు మరియు భూమికి మధ్యదూరం = x

ప్రశ్న 30.
సోనార్ (SONAR) (sound navigation and ranging) అనే సాధనం నీటి అడుగున ఉండే వస్తువులను వాటి స్థానాలను శోధించడానికి అతిధ్వని తరంగాలను ఉపయోగిస్తుంది. ఒక సబ్మెరైన్ (జలాంతర్గామి) లోని సోనార్ నుంచి వెలువడిన శోధక తరంగ ఉత్పత్తికి, శతృదేశ జలాంతర్గామిపై పరావర్తనం తరవాత పొందే ప్రతిధ్వనుల మధ్య కాల విలంబనం (time delay) 77.0 s అని కనుక్కొన్నారు. శతృదేశ సబ్మెరైన్ దూరం ఎంత ? (నీటిలో ధ్వని = 1450 ms^-1).
సాధన:
ఇక్కడ t = 77.0 sec, υ = 1450 ms^-1

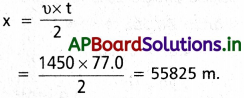
ప్రశ్న 31.
ఇంతవరకూ ఆవిష్కరించిన, మన విశ్వంలోని అత్యంత దూరంలో గల వస్తువులు ఎంత దూరంలో ఉంటాయంటే అవి ఉద్గారించే కాంతి భూమిని చేరుకోవడానికి బిలియన్ల సంవత్సరాలు పడుతుంది. (క్వాజార్ (quasars) అని పిలిచే) ఈ వస్తువులకు అనేకమైన దిగ్రమ కలిగించే లక్షణాలుంటాయి. ఈ లక్షణాలను ఇంతవరకు ఎవరూ సంతృప్తికరమైన వివరణ ఇవ్వలేకపోయారు. ఒక క్వాజార్ నుంచి వెలువడే కాంతి మనల్ని చేరుకోవడానికి 3.0 బిలియన్ల సంవత్సరాలు పడితే km లలో దాని దూరం ఎంత?
సాధన:
పట్టుకాలం t = 3 బిలియన్ సంవత్సరాలు
= 3 × 10⁹ సంవత్సరాలు
= 3 × 10⁹ × 365 × 24 × 60 × 60 sec

శూన్యంలో కాంతివేగం, c = 3 × 10⁸ m/s
= 3 × 10⁵ m/s

దూరం = వేగం × కాలం
x = 3 × 10⁵ × 3 × 10⁹ × 365 × 24 × 60 × 60 km.
x = 2.84 × 10²² km

ప్రశ్న 32.
సంపూర్ణ సూర్యగ్రహణం ఏర్పడినపుడు చంద్రుడు ఒక బిళ్లవలె సూర్యబింబాన్ని దాదాపుగా పూర్తిగా కప్పివేస్తాడని మనకు బాగా తెలిసిన వాస్తవం. దీని నుంచి, ఉదాహరణలు 3, 4 లోని సమాచారం ఆధారంగా చంద్రుడి ఉజ్జాయింపు వ్యాసాన్ని నిర్ణయించండి.
సాధన:
చంద్రుడి నుండి భూమి వరకు దూరం = 3.84 × 10⁸ m
భూమి నుండి సూర్యుడి వరకు దూరం = 1.496 × 10¹¹ m

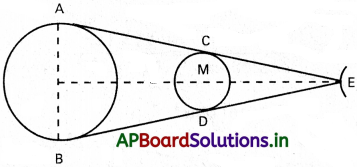
సూర్యుడు AB వ్యాసం = 1.39 × 10⁹ m
∆^le ABE, ∆^le CDEలు సర్వసమాన త్రిభుజాలు

CD = 3567.9 km ఇది చంద్రుడి వ్యాసం

ప్రశ్న 33.
ఈ శతాబ్దంలోని గొప్ప భౌతికశాస్త్రవేత్త అయిన P.A.M. Dirac ప్రకృతిలోని ప్రాథమిక స్థిరాంకాల సంఖ్యాత్మక విలువలతో ఆడుకోవడాన్ని ఎంతో ఇష్టపడేవాడు. ఈ ఆట అతణ్ణి ఒక ఆసక్తిదాయకమైన పరిశీలనవైపు నడిపించింది. పరమాణు భౌతికశాస్త్రం మూల స్థిరాంకాలు (c, e ఎలక్ట్రాన్ ద్రవ్యరాశి, ప్రోటాన్ ద్రవ్యరాశి), గురుత్వ స్థిరాంకం G నుంచి ‘కాలం’ మితిగల ఒక సంఖ్యను చేరుకోవచ్చని డిరాక్ కనుక్కొన్నాడు. పైగా, అది చాలా పెద్ద సంఖ్య. అంటే దాని పరిమాణం విశ్వం వయస్సుపై మనకున్న నేటి అంచనాకు (~ 15 బిలియన్ సంవత్సరాలు) చాలా దగ్గరగా ఉంటుందని తెలిసింది. ఈ పుస్తకంలో ఇచ్చిన ప్రాథమిక స్థిరాంకాలకు సబంధించిన పట్టిక నుంచి నీవు కూడా ఈ సంఖ్యను నిర్మించగలవేమో ప్రయత్నించి చూడు (లేదా మరేదైనా, నీవు ఆలోచించగలిగే ఆసక్తిదాయకమైన సంఖ్యను కనుక్కోవచ్చు).ఈ విశ్వం వయస్సుతో ఈ సంఖ్య ఏకీభవించడమనేది ఒకవేళ ఉపేక్షించదగనిది అయితే ప్రాథమిక స్థిరాంకాలకు ఉండే స్థిరత్వం (constancy) పట్ల ఇది ఏ అర్థాన్ని సూచిస్తుంది?
సాధన:
కాంతి వేగం, ఆ ఎలక్ట్రాన్ యొక్క ఆవేశం, m^p ప్రోటాన్ ద్రవ్యరాశి, m^e ఎలక్ట్రాన్ ద్రవ్యరాశి, G విశ్వగురుత్వ స్థిరాంకం.

ఇది విశ్వం యొక్క వయస్సు.

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
కోణాలు (a) 1 (డిగ్రీ) (b) 1′ (చాపం యొక్క నిమిషం లేదా ఆర్మిన్), (c) 1″ (చాపం యొక్క సెకను లేదా ఆర్క్ సెకను) రేడియన్లలో లెక్కించండి. 360° = 2π rad, 1° = 60′ 1′ = 60″ లను ఉపయోగించండి.
సాధన:
(a) 360° = = 2π rad నుంచి
1° = (π/180) rad = 1.745 × 10^-2

(b) 1° = 60′ = 1.745 × 10^-2 rad
1’= 2.908 × 10^-4 rad, 2.91 × 10^-4 rad

(c) 1′ = 60″ = 2.908 × 104 rad
1″ = 4.847 × 10^-6 rad, 4.85 × 10^-6 rad.

ప్రశ్న 2.
ఒక వ్యక్తి తనకు సమీపంలో ఉండే శిఖరం (tower) దూరాన్ని అంచనా వేయాలను కొన్నాడు. శిఖరం C కు ఎదురుగా ఉండే బిందువు A వద్ద నిల్చొని, చాలా దూరంలో ఉండే వస్తువు 0 ను ACరేఖ వెంట ఉండటం గుర్తించాడు. అపుడు AC కి లంబ దిశలో 100 m దూరం బిందువు B వరకు నడిచాడు. తరువాత O, C ల వైపు మళ్ళీ చూశాడు. ౦ ఎక్కువ దూరంలో ఉంది కాబట్టి వాస్తవంగా BO దిశ AO దిశ ఒకటే అవుతాయి, కానీ, C దృష్టి రేఖ, మౌలికంగా ఉన్న దృష్టి రేఖ నుంచి θ = 40° కోణం విస్థాపనం చెందినట్లు గుర్తించాడు. (θను దృష్టి విక్షేపం అంటారు) అతని తొలిస్థానం A నుంచి టవర్ C దూరాన్ని అంచనా వేయండి.

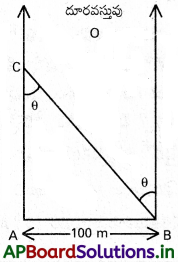
సాధన:
పారలాక్స్ కోణం θ = 40°;
పటం నుంచి AB = AC tan θ
AC = AB/tan θ = 100 m/tan 40°
= 100 m/0.8391 = 119 m.

ప్రశ్న 3.
భూమి వ్యాసంపై ఉండే రెండు వ్యతిరేక బిందువులు A,B ల నుంచి, చంద్రుడిని పరిశీలించారు. చంద్రుడి వద్ద రెండు పరిశీలనా దిశలు ఏర్పరిచే కోణం 8 విలువ 1’54’. భూమి వ్యాసం సుమారుగా 1.276 × 10⁷m అయితే, భూమి నుంచి చంద్రుని దూరాన్ని లెక్కించండి.
సాధన:
దత్తాంశం నుంచి θ = 1°54′ = 114′
= (114 × 60)” × (4.85 × 10^-6) rad
1″ = 4.85 × 10^-6 rad కాబట్టి,
θ = 3.32 × 10^-2 rad,
అంతేగాక, b = AB = 1.276 × 10⁷ m
భూమి -చంద్రుల మధ్య దూరం

ప్రశ్న 4.
సూర్యుడి కోణీయ వ్యాసం 1920″ అని కొలిచారు. భూమి నుంచి సూర్యుడి దూరం D విలువ 1.496 × 10″ m. అయితే సూర్యుడి వ్యాసం ఎంత?
సాధన:
సూర్యుడి కోణీయ వ్యాసం, α = 1920″
= 1920 × 4.85 × 10^-6 rad
= 9.31 × 10^-3 rad
సూర్యుడి వ్యాసం, d = α D
= (9.31 × 10^-3) × (1.496 × 10¹¹) m
= 1.39 × 10⁹ m.

ప్రశ్న 5.
కేంద్రక పరిమాణాన్ని (10-15 నుంచి 10-14 m వ్యాప్తిలో) నిశితమైన పిన్ను కొనతో పోల్చితే, పరమాణు పరిమాణం సుమారుగా ఎంత ఉంటుంది ? పిన్ను కొన 10 m నుంచి 104 m వ్యాప్తిలో ఉన్నదనుకోండి.
సాధన:
కేంద్రక పరిమాణం 10^-15 m నుంచి 10^-14 m వ్యాప్తిలో ఉంది. నిశితమైన పిన్ను చివర 10^-5 m నుంచి 10^-4 m వ్యాప్తిలో ఉన్నదని అనుకొంటే మనం పరిమాణ విలువను 10¹⁰ కారకంతో పెంచుతున్నామన్నమాట. కాబట్టి పరమాణువుకు 10^-10 m (దాదాపు) పరిమాణం ఉన్నప్పుడు దానిని 1 m పరిమాణానికి పెంచినామన్న మాట. అంటే పరమాణువు లోపలి కేంద్రకం పరిమాణం దాదాపు 1 మీటరు పొడవు వ్యాసార్ధం ఉన్న గోళం కేంద్రం వద్ద ఉంచిన నిశిత పిన్ను కొన అంత చిన్నదిగా ఉంటుంది.

ప్రశ్న 6.
ఒక జాతీయ పరిశోధనాశాలలోని ప్రామాణిక గడియారంతో పోలుస్తూ రెండు గడియారాల పనితీరును పరీక్షిస్తున్నారు. ప్రామాణిక గడియారం మధ్యాహ్నం 12 : 00:00 సమయాన్ని సూచిస్తున్నప్పుడు ఆ రెండు గడియారాల్లోని రీడింగులు ఈవిధంగా ఉన్నాయి.

	గడియారం 1	గడియారం 2
సోమవారం	12:00:05	10:15:06
మంగళవారం	12:01:15	10:14:59
బుధవారం	11:59:08	10:15:18
గురువారం	12:01:50	10:15:07
శుక్రవారం	11:59:15	10:14:53
శనివారం	12:01:30	10:15:24
ఆదివారం	12:01:19	10:15:11

ఖచ్చితత్వం కలిగిన కాలవ్యవధుల కొలతలు అవసరమయ్యే ప్రయోగాన్ని నీవు చేస్తున్నావని అనుకొంటే, పై రెండు గడియారాల్లో దేన్ని ఎంచుకొంటావు?
సాధన:
ఏడు రోజులపాటు చేసే పరిశీలనల్లో మొదటి గడియారం (1) సమయాల్లో వచ్చే మార్పుల వ్యాప్తి 162 5 కాగా, రెండో గడియారానికి (2) 31 5 అవుతుంది. గడియారం (1) చూపే సగటు రీడింగ్, గడియారం (2) చూపే సగటు రీడింగ్ కంటే ప్రామాణిక కాలానికి చాలా దగ్గరగా ఉంది. ఇక్కడ గమనించవలసిన ముఖ్యమైన అంశం ఏమంటే ఖచ్చితత్వం అవసరమయ్యే ప్రయోగాలకు గడియారం చూపే వ్యాప్తియే ప్రధానం కాని అది చూపే శూన్యదోషం కాదు. ఎందుకంటే, ‘శూన్యదోషాన్ని’ ఎప్పుడైనా సులువుగా సవరించుకోవచ్చు. కాబట్టి గడియారం (1) కంటే రెండో గడియారాన్నే ఎంచుకోవాల్సి ఉంటుంది.

ప్రశ్న 7.
లఘులోలకం డోలనావర్తన కాలాన్ని కొలుద్దాం. వరుస కొలతల్లో వచ్చిన రీడింగ్లు 2.63s, 2.56, 2.42 s, 2.71, చివరగా 2.80s. పరమదోషాలను, సాపేక్షదోషం లేదా దోష శాతాన్ని లెక్కించండి.
సాధన:
లోలకం సగటు డోలనావర్తన కాలం

ప్రశ్న 8.
థర్మామీటరుతో రెండు వస్తువుల ఉష్ణోగ్రతలను t₁ = 20 °C ± 0.5 °C, t₂ = 50°C ± 0.5°C గా కొలిచారు. వాటి ఉష్ణోగ్రతా భేదాన్ని, దానిలోని దోషాన్ని లెక్కించండి.
సాధన:
t’ = t₂ – t₁
= (50 °C ± 0.5 °C) – (20 °C ± 0.5 °C)
t’ = 30 °C ± 1 °C.

ప్రశ్న 9.
నిరోధం R = V/I ఇందులో V = (100 ± 5) V, I = (10 ± 0.2) A. అయితే లోని దోషశాతాన్ని కనుక్కోండి.
సాధన:
V లోని దోష శాతం 5, అలాగే I లో దోష శాతం 2.
కాబట్టి R లో మొత్తం దోషం 5 + 2 = 7%.

ప్రశ్న 10.
రెండు నిరోధకాల నిరోధాలు R₁ = 100 ± 3 ohm, R₂ = 200 ± 4 ohm. వీటిని (a) శ్రేణిలో, (b) సమాంతరంగా కలిపారు. (a) శ్రేణీ సంయోగానికి, (b) సమాంతర సంయోగానికి తుల్య నిరోధాలను కనుక్కోండి. సూచన :

సాధన:
a) శ్రేణి సంయోగానికి తుల్య నిరోధం
R = R₁ + R₂ = (100 ± 3)
ohm + (200 ± 4) ohm = 300 ± 7 ohm

b) సమాంతర సంయోగానికి తుల్య సంబంధం

అప్పుడు R’ = 66.7 ± 1.8 ohm
(ఇక్కడ ∆R విలువను, 2గా సూచించడానికి బదులు 1.8 గానే వ్యక్తం చేశాం. `ఎందుకంటే, సార్థక సంఖ్యల నియమాలకు అనుగుణంగా ఉండటం కోసం).

ప్రశ్న 11.
Z = A⁴B^1/3/CD^3/2 అయితే 2 లో సాపేక్ష దోషాన్ని కనుక్కోండి.
సాధన:
Z లో సాపేక్ష దోషం, ∆Z/Z = 4(∆A/A) + (1/3) (∆B/B) + (∆C/C) + (3/2) (∆D/D).

ప్రశ్న 12.
లములోలకం డోలనావర్తన కాలం = 2π √L/g . 1 mm తెలిసిన యదార్థతతో కొలచిన L విలువ 20.0 cm. 100 డోలనాలకు పట్టిన కాలాన్ని 1s పృథక్కరణం ఉన్న చేతి గడియారంతో 90 s అని కనుక్కొన్నారు. అయితే g విలువను నిర్ణయించడంలో యదార్ధత ఎంత?
సాధన:
g = 4π²L/T²; ఇక్కడ T = \(\frac{t}{n}\), ∆T = \(\frac{\Delta t}{n}\)
కాబట్టి, \(\frac{\Delta T}{T}=\frac{\Delta t}{t}\) ఈ L, t రెండింటిలోని దోషాలు
కనీసపు కొలత దోషాలు కాబట్టి
(∆g/g) = (∆L/L) + 2(∆T/T)
= \(\frac{0.1}{20.0}\) + 2(\(\frac{1}{90}\)) = 0.027
అందువల్ల g లోని దోషశాతం
100 (∆g/g) = 100(∆L/L) + 2 × 100 (∆T/T) = 3.

ప్రశ్న 13.
ఒక ఘనం యొక్క ఒక్కొక్క భుజం పొడవును 7.203 m గా కొలిచారు. దాని మొత్తం ఉపరితల వైశాల్యం, ఘనపరిమాణాల విలువలను తగిన సార్ధక సంఖ్యల వరకు కనుక్కోండి.
సాధన:
కొలిచిన పొడవులో నాలుగు సార్థక సంఖ్యలు ఉండటం వల్ల మనం లెక్కించే వైశాల్యం, ఘనపరిమాణాలను కూడా నాలుగు సార్ధక సంఖ్యల వరకే సవరించవలసి ఉంటుంది.
ఘనం ఉపరితల వైశాల్యం = 6(7.203)² m²
= 311.299254 m²
= 311.3 m²

ఘనం ఘనపరిమాణం = (7.203)³ m³
= 373.714754 m³
= 373.7 m³.

ప్రశ్న 14.
5.74 g పదార్థం 1.2 cm3 ఘనపరిమాణం ఆక్రమిస్తుంది. సార్ధక సంఖ్యలను దృష్టిలో ఉంచుకొని దాని సాంద్రత విలువను వ్యక్తపరచండి.
సాధన:
కొలచిన ద్రవ్యరాశిలో మూడు సార్ధక సంఖ్యలు ఉంటే కొలచిన ఘనపరిమాణంలో రెండే సార్థక సంఖ్యలు ఉన్నాయి. కాబట్టి, సాంద్రత విలువను 2 సార్థక సంఖ్యల వరకు మాత్రమే వ్యక్తపరచాలి.
సాంద్రత = \(\frac{5.74}{1.2}\) g cm^-3 = 4.8 g cm^-3.

ప్రశ్న 15.
\(\frac{1}{2}\)mυ² = mgh అనే ఒక సమీకరణాన్ని పరిగణిద్దాం. ఇందులో m అనేది వస్తువు ద్రవ్యరాశి, υ దాని వేగం, g గురుత్వ తరణం, h దాని ఎత్తు. ఈ సమీకరణం మితీయంగా సరియైందో కాదో పరీక్షించి చూడండి.
సాధన:
ఎడమవైపు (LHS) ఉన్న మితులు
[M] [LT^-1]² = [M] [L²T^-2] = [M L²T^-2]
కుడివైపు (RHS) ఉన్న మితులు
[M] [LT^-2] [L] = [M] [L²T^-2] = [M L²T^-2]
LHS, RHS లలోని మితులు ఒకటే కాబట్టి సమీకరణం మితీయంగా సరైనది.

ప్రశ్న 16.
శక్తికి SI ప్రమాణం J = kg m²s^-2; అదేవిధంగా వడి υ, త్వరణం a కు ప్రమాణాలు వరుసగా ms^-1, ms^-2. అయితే గతిజశక్తి (K) కి కింద ఇచ్చిన ఫార్ములాల్లో మితీయంగా దేనిని క్రమ విరుద్ధమైనదిగా తోసిపుచ్చుతావు? (m వస్తువు ద్రవ్యరాశిని సూచిస్తుంది)
(a) K = m²υ³ (b) K = (1/2) mυ²
(c) K = = ma (d) K = (3/16) mυ²
(e) K = (1/2) mυ² + ma.
సాధన:
ప్రతి సరైన సమీకరణం లేదా ఫార్ములాలో ‘సమీకరణానికి రెండువైపులా ఒకే మితులు ఉండాలి. అదేవిధంగా ఒకే రకమైన మితులుండే రాశులను మాత్రమే సంకలనం లేదా వ్యవకలనం చేయాలి. కుడివైపు గల రాశికి మితులు (a) విషయంలో[M²L³T^-3], (b), (d) లకు [ML²T^-2] (c)కి [MLT^-2], (e) కి కుడివైపునున్న రాశికి సరియైన మితులు లేవు. ఎందుకంటే భిన్న మితులు కలిగిన రెండు రాశులను కలపడమైంది. గతిజ శక్తి Kకి ఉండే మితులు [ML²T^-2] కాబట్టి (a), (c), (e) ఫార్ములాలను తోసిపుచ్చవలసిందే. అయితే, మిగతా రెండు ఫార్ములాలు (b) లేదా (d) లలో ఏది సరియైనదో మితుల ద్వారా చెప్పలేం. అందుకని, గతిజ శక్తికి ఇచ్చిన (అధ్యాయం లో) నిజ నిర్వచనం ప్రకారం, గతిజ శక్తికి సరియైన ఫార్ములాను (b) సూచిస్తుంది.

ప్రశ్న 17.
దారానికి గుండు తగిలించిన లఘులోలకాన్ని పరిగణించండి. గురుత్వ బల చర్య వల్ల ఇది డోలనాలను చేస్తుంది. లోలకం డోలనావర్తన కాలం(T), పొడవు(1), గుండు ద్రవ్యరాశి (m), గురుత్వ త్వరణం(g) లపై ఆధారపడుతుందను కోండి. ‘మితుల పద్ధతిని ఉపయోగించి దాని ..డోలనావర్తన కాలానికి సమాసాన్ని ఉత్పాదించండి.
సాధన:
l, g, m రాశులపై డోలనావర్తన కాలం T ఆధారపడటాన్ని వాటి లబ్ధంగా ఇలా రాయవచ్చు.
T = k l^x g^y m^z

ఇక్కడ k మితిరహిత స్థిరాంకం, x, y, z లు ఘాతాంకాలు. ఇరువైపులా మితులను తీసుకొంటే,
[L°M°T¹] = [L¹]^x [L¹T^-2]^y [M¹]^z = L^{x + y} T^-2y M^z
ఇరువైపులా ఉన్న మితులను సమానం చేస్తే,
x + y = 0; -2y = 1; z = 0
అందువల్ల, x = \(\frac{1}{2}\), y = –\(\frac{1}{2}\), z = 0
అప్పుడు T = kl^1/2 g^-1/2 లేదా T = k\(\sqrt{\frac{l}{g}}\)

k విలువను మితుల పద్ధతి ద్వారా కనుక్కోలేమని గమనించండి. ఇక్కడ కుడివైపు ఉన్న ఫార్ములాను ఏదో ఒక సంఖ్యతో గుణించినంత మాత్రాన ఎలాంటి ప్రభావం ఉండదు. ఎందుకంటే ఆ సంఖ్య దాని మితులను ప్రభావితం చేయదు.
నిజానికి k = 2π. అందువల్ల,
T = 2π \(\sqrt{\frac{l}{g}}\)