AP Inter 1st Year Physics Study Material Chapter 4 సమతలంలో చలనం

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 4th Lesson సమతలంలో చలనం Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 4th Lesson సమతలంలో చలనం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఒక సదిశ నిలువు అంశం దాని క్షితిజ సమాంతర అంశానికి సమానం. ఆ సదిశ x అక్షంతో చేసే కోణం ఎంత ?
జవాబు:

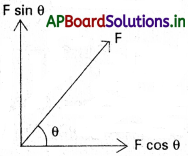
క్షితిజ సమాంతర అంశము = క్షితిజ లంబ అంశము
F cos θ = F sin θ
Tan θ = 1
θ = Tan^-1 (1) = 45°

ప్రశ్న 2.
ఒక సదిశ V క్షితిజ సమాంతరంతో e కోణం చేస్తుంది. ఆ సదిశను e కోణం భ్రమణం చెందించడమైంది. ఈ భ్రమణం సదిశ V లో మార్పు తెస్తుందా?
జవాబు:
అవును, ఇది సదిశను మారుస్తుంది.

ప్రశ్న 3.
3 ప్రమాణాలు, 5 ప్రమాణాల పరిమాణం ఉన్న రెండు బలాలు ఒకదానితో ఒకటి 60° కోణంలో పనిచేస్తున్నాయి. వాటి ఫలిత పరిమాణం ఎంత?
జవాబు:
P = 3 = 3 యూనిట్లు, Q = 5 యూనిట్లు, Q = 60°

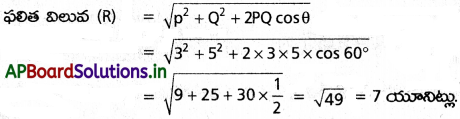
ప్రశ్న 4.
A = \(\overrightarrow{i} + \overrightarrow{j}\) ఈ సదిశ x – అక్షంతో చేసే కోణం ఎంత? [Mar. ’14, ’13]
జవాబు:
A = \(\overrightarrow{i}+\overrightarrow{j}\)

ప్రశ్న 5.
7 యూనిట్లు, 24 యూనిట్లు పరిమాణం ఉన్న రెండు లంబ సదిశలు సంయోగం చెందినట్లైతే ఫలిత సదిశ పరిమాణం ఎంత?
జవాబు:
θ = 90°, P = 7 యూనిట్లు, Q = 24 యూనిట్లు

ప్రశ్న 6.
P = 2i + 4j + 14k, Q = 4i + 4j + 10k అయితే P + Q పరిమాణం కనుక్కోండి.
జవాబు:
P = 2i + 4j + 14k, Q = 4i + 4j + 10k,
\(\overrightarrow{P}+\overrightarrow{Q}\) = 2i + 4j + 14k + 4i + 4j + 10k.
= 6i + 8j + 24k

ప్రశ్న 7.
శూన్య పరిమాణం కలిగిన సదిశకు శూన్యం కాని అంశాలు ఉంటాయా?
జవాబు:
లేదు. సున్నా పరిమాణం గల ఒక సదిశ శూన్యేతర అంశాలను కలిగి ఉండదు.

ప్రశ్న 8.
ప్రక్షేపకం యొక్క ప్రక్షేప పథం అగ్రభాగంలో దాని త్వరణం ఎంత?
జవాబు:
ప్రక్షేపకం యొక్క పథంలో గరిష్ఠ బిందువు వద్ద త్వరణం నిట్టనిలువుగా క్రిందకు ఉంటుంది.

ప్రశ్న 9.
రెండు అసమ పరిమాణం ఉన్న సదిశల సంకలన మొత్తం శూన్య సదిశను ఇవ్వగలదా? మూడు అసమాన సదిశలు కలిసి శూన్య సదిశను ఇవ్వగలవా?
జవాబు:

1. లేదు. అసమ పరిమాణంగల రెండు సదిశల మొత్తం శూన్య సదిశకాదు.
2. అవుతుంది. త్రిభుజ నియమం ప్రకారం సమతాస్థితిలో మూడు అసమ సదిశల మొత్తం శూన్యమవుతుంది.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సదిశల సమాంతర చతుర్భుజ నియమాన్ని పేర్కొనండి. ఫలిత సదిశ పరిమాణం, దిశలకు సమీకరణం రాబట్టండి. [Mar. 14, ’13]
జవాబు:
సమాంతర చతుర్భుజ నియమం :
రెండు సదిశలు పరిమాణంలోను, దిశలోను ఒక బిందువు నుండి గీసిన సమాంతర చతుర్భుజం యొక్క రెండు ఆసన్న భుజాలను సూచిస్తే, వాటి ఫలిత సదిశ పరిమాణంలోను, దిశలోను అదే బిందువు గుండా పోయే కర్ణాన్ని సూచిస్తుంది.

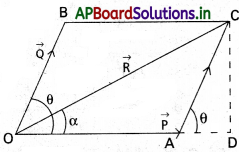
వివరణ :
రెండు బల సదిశలు \(\overrightarrow{P}\) మరియు \(\overrightarrow{Q}\) లు ౦బిందువు వద్ద పనిచేస్తున్నాయి. రెండు బలాల మధ్య కోణం θ. OA = \(\overrightarrow{P}\) మరియు OB = \(\overrightarrow{Q}\) అనుకొనుము. OACB సమాంతర చతుర్భుజంను పూర్తిచేయాలి. O మరియు C బిందువులను కలపాలి. ఇప్పుడు OC = \(\overrightarrow{R}\)

ఫలిత పరిమాణం :
పటంలో \(\overrightarrow{OA}= \overrightarrow{P},\overrightarrow{OB}=\overrightarrow{Q},\overrightarrow{OC}=\overrightarrow{R}\)
COD త్రిభుజం నుండి OC² = OD² + CD²
OC² = (OA + AD)² + CD² (∵ OD = OA + AD)
OC² = OA² + AD² + 20A . AD + CD²
OC² = OA² + AC² + 20A . AD …………. (1)
CAD త్రిభుజం నుండి, AD² + CD²
∆^le CAD cos θ = \(\frac{AD}{AC}\)
AD = AC cos θ …………. (2)
∴ R² = P² + Q² + 2PQ cos θ
R = \(\sqrt{P^2+Q^2 +2PQ cos \theta}\) …………. (2)

ఫలితదిశ :

ప్రశ్న 2.
సాపేక్ష చలనం అంటే ఏమిటి? వివరించండి.
జవాబు:

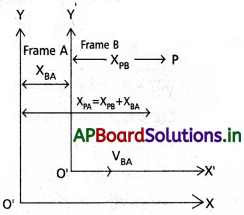
సాపేక్షవేగం :
ఒక వస్తువు యొక్క వేగాన్ని రెండవ వస్తువు దృష్ట్యా చెప్పటాన్ని సాపేక్ష వేగం అంటారు.

ప్రక్కపటంలో చూపినట్లు అంతరాళంలో Pఒక ఘటన అనుకొనుము. A మరియు B అనే పరిశీలకులు తమతమ నిరూపక వ్యవస్థల మూల బిందువుకు ఆపాదించుకున్నారనుకొనుము.

A పరంగా B పరిశీలకుడు V_BA స్థిరవేగంతో చలిస్తున్నాడనుకొనుము. ఇప్పుడు A పరంగా P ఘటన స్థాన కొలతను B పరంగా P ఘటన స్థానకొలతను అను సంధానం చేశామనుకొనుము.

Pను పరిశీలించేసమయమునకు Bనిర్దేశిక వ్యవస్థ పరంగా ప్రయాణించిన దూరం = X_BA

ఘటన Pజరిగిన స్థానాల మధ్య సంబంధం
X_PA = X_PB + X_BA → (1)

A పరంగా P యొక్క స్థానము = Bపరంగా P యొక్క స్థానం + Aపరంగా B యొక్క స్థానం అదే విధంగా సమీకరణం (1)ని ఇలా కూడా వ్రాయవచ్చు.
V_PA = V_PB + V_BA → (2)
Aపరంగా Pయొక్క వేగం = Bపరంగా Pయొక్క వేగం + Aపరంగా B యొక్క వేగం

ప్రశ్న 3.
కనిష్ఠ కాలంలో నదిని దాటడానికి నావ నది నీటితో కొంత కోణం చేస్తూ ప్రయాణం చేయాలని చూపండి.
జవాబు:

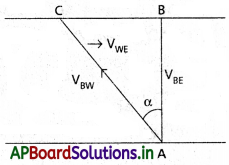
నావ నది ఒడ్డున గల Aనుండి, ఆవలి ఒడ్డున ఉన్న బిందువు Bవైపు AB మార్గంలో ప్రయాణిస్తున్నది అనుకొనుము. ఫలితవేగము V ge దిశ AB వైపు ఉంటుంది.

V_BW వేగంతో నావ కదిలితే ఎదురుగా ఉన్న Bబిందువును చేరడానికి, AB తో α కోణం చేయునట్లుగా ప్రవాహానికి ఎదురుగా ప్రయాణించాలి. ఇక్కడ V_BW నీటి పరంగా పడవవేగం.

ప్రశ్న 4.
ప్రమాణ సదిశ, శూన్య సదిశ, స్థానాంతర సదిశలను నిర్వచించండి.
జవాబు:

ప్రమాణ సదిశ :
ఒక సదిశ యొక్క పరిమాణము ఏకాంకమైతే దానిని ఏకాంక సదిశ అంటారు.

శూన్య సదిశ :
పరిమాణము శూన్యంగా గల సదిశను శూన్యసదిశ అంటారు.

స్థాన సదిశ :
ఒక నిర్ధేశ చట్రం యొక్క మూల బిందువు నుండి కణస్థానం వద్దకు గీసిన స్థాన సదిశతో ఒక కణస్థానాన్ని గుర్తిస్తారు. దానినే స్థాన సదిశ అంటారు. అంతరాళంలో ఒక కణంను గుర్తించడానికి ఇది ఉపయోగపడుతుంది. కణం P యొక్క స్థాన సదిశను \(\overrightarrow{OP}\) గా వ్రాస్తారు.

ప్రశ్న 5.
ల మధ్య కోణం 90° అని చూపండి.
జవాబు:

2ab cos θ = – 2ab cos θ
4ab cos θ
cos θ = 0 4ab ≠ 0
∴ θ = 90°
కాబట్టి \(\overrightarrow{a}\) మరియు \(\overrightarrow{b}\) మధ్యకోణం 90°.

ప్రశ్న 6.
క్షితిజ సమాంతర దిశకు కొంత కోణం చేస్తూ విసిరిన వస్తువు (ప్రక్షిప్త) పథం పరావలయం అని చూపండి. [May ’13]
జవాబు:

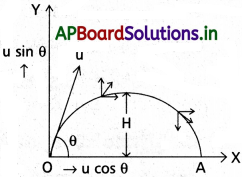
ఒక వస్తువును క్షితిజ సమాంతరంతో రికోణం చేయునట్లుగా u తొలివేగంతో ప్రక్షిప్తం చేశామనుకొనుము. వస్తువు క్షితిజ సమాంతరం దిశ త్వరణానికి లోను కాదు. ప్రక్షేపకం వేగాన్ని రెండు అంశాలుగా విభజించవచ్చు. (i) క్షితిజ సమాంతర అంశము u cos θ (ii) క్షితిజ లంబ అంశము u sin θ. క్షితిజ సమాంతర అంశము చలనం అంతటా స్థిరంగా ఉంటుంది. కేవలం క్షితిజ లంబ అంశం u sin θ గురుత్వ త్వరణం వలన మారుతుంది.
tకాలంలో OX దిశలో ప్రయాణించిన దూరం
x = u cos θ × t
t = \(\frac{x}{u \cos \theta}\) → (1)
t కాలంలో OY దిశలో ప్రయాణించిన దూరం

Y = Ax – Bx² ఇక్కడ A, B లు స్థిరాంకాలు
ఈ సమీకరణం పరావలయాన్ని సూచిస్తుంది.
∴ ప్రక్షేపకం యొక్క పథం· కూడా పరావలయం అవుతుంది.

ప్రశ్న 7.
సగటు వేగం, తాక్షణిక వేగం పదాలను వివరించండి. ఈ రెండు ఎప్పుడు సమానం అవుతాయి?
జవాబు:
సగటువేగం :
స్థానభ్రంశం (∆x) కు, కాల అవధి At కు గల నిష్పత్తిని సగటువేగం అంటారు.

తొలి మరియు తుది స్థానాల మధ్య కణం అనుసరించే మార్గంపై సగటువేగం ఆధారపడదు. ఇది ఫలితచలనాన్ని ఇస్తుంది.

తాక్షణిక వేగం :
ఒక నిర్ధిష్ట కాలం వద్ద కణం వేగాన్ని తాక్షణిక వేగం అంటారు.

సరళరేఖా చలనంలో తాక్షణిక వేగం ధనాత్మకం (లేదా) ఋణాత్మకం కావచ్చు.
ఏకరీతి చలనంలో వస్తువు యొక్క తాక్షణిక వేగం, సగటు వేగానికి సమానం.

ప్రశ్న 8.
ఒక ప్రక్షేపకం యొక్క గరిష్లోన్నతి మరియు వ్యాప్తులు వరుసగా

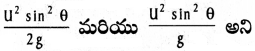
చూపండి. ఇక్కడ వాడిన పదాలను సాధారణంగా ఉపయోగించే అర్థంలోనే వాడాం. [Mar. ’14]
జవాబు:
గరిష్తోన్నతి :
ప్రక్షేపకం క్షితిజలంబదిశలో, లంబాంశవేగము శూన్యం అయ్యేవరకు ప్రయాణించిన దూరాన్ని గరిష్టోన్నతి అంటారు.

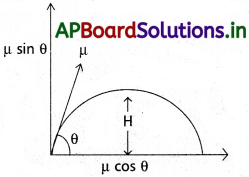
తొలి వేగం (u) = u sin θ
దూరం (s) = H = గరిషోన్నతి
త్వరణం (a) – g
v² – u² = 2as ను ఉపయోగించి
0 – u² sin² θ = – 2gH
∴ H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)

క్షితిజ సమాంతరవ్యాప్తి (R)
క్షితిజ సమాంతరదిశలో పలాయన కాలంలో ప్రక్షేపకం ప్రయాణించిన దూరాన్ని క్షితిజ సమాంతర వ్యాప్తి అంటారు.
వ్యాప్తి (R) = క్షితిజ సమాంతర వేగం × ప్రయాణ కాలం

ప్రశ్న 9.
ఒక నిర్దేశ చట్రంలో వస్తువు ప్రక్షిప్త పథం పరావలయం అయితే, ఈ నిర్దేశ చట్రంతో సాపేక్షంగా స్థిరవేగంతో కదులుతున్నా మరొక నిర్దేశ చట్రంలో కూడా వస్తువు పథం పరావలయ ఆకృతిలో ఉంటుందా? ఒకవేళ ప్రక్షేపక పథం పరావలయం కాకపోతే అది ఏ ఆకృతిలో ఉంటుంది?
జవాబు:
కాదు. సమవేగంలో ఉన్న బస్సునుండి ఒకరాయిని బయటకు విసిరామనుకోండి. వెలుపల ఫుట్పాట్పై నిలబడి ఉన్న వ్యక్తి ఆరాయి పరావలయ పథంలో కనిపిస్తుంది. కాని అదే బస్సులో ఉన్న వ్యక్తికి అది సరళరేఖామార్గంలో కనిపిస్తుంది. కాబట్టి వేరు వేరు నిర్దేశిక చట్రాల పరంగా వస్తువు యొక్క పథం వేరువేరుగా ఉంటుంది.

ప్రశ్న 10.
నిశ్చల స్థితిలో ఉన్న వస్తువుపై 2i + j – k న్యూటన్ల బలం పనిచేస్తుంది. 20 సెకనుల చివర వస్తువు వేగం 4i + 2j + 2k ms^-1 అయితే ఆ వస్తువు ద్రవ్యరాశి ఎంత?
జవాబు:
F = (2i + j – k) N
t = 20 sec, u = 0
v = (4i + 2j – 2k) m/s

లెక్కలు (Problems)

ప్రశ్న 1.
ఓడ B కి ఓడ A పశ్చిమదిశలో 10km దూరంలో ఉంది. ఓడ A నేరుగా ఉత్తర దిక్కువైపు 30 km/h వడితో వెళుతుంటే, ఓడ B ఉత్తర దిశతో పడమరవైపు 60° కోణం చేస్తూ 20 km/ h వడితో వెళుతుంది.
i) ఓడ Aకి సాపేక్షంగా ఓడ B వేగ పరిమాణాన్ని, దిశను కనుక్కోండి.
ii) రెండింటి మద్య అత్యంత సమీపదూరం (closest approach) ఎంత?
సాధన:
i) V_A = 30 kmph, V_B = 20 kmph, θ = 60°
B నౌక యొక్క సాపేక్ష వేగం A నౌక పరంగా,

ii) నౌక A మరియు B మధ్య దూరం = 10 km.
B నౌక పరంగా A నౌక ఉత్తరం వైపు ప్రయాణిస్తోంది. రెండింటి మధ్య దగ్గర దూరం BD = AB sin 45°

ప్రశ్న 2.
ప్రక్షేపక కోణం α వ్యాప్తి R, గరిష్ఠ ఎత్తు h ప్రయాణ కాలం T అయితే (a) tan α = 4h/R,
(b) h = gT²/8 అని చూపండి.
సాధన:

ప్రశ్న 3.
క్షితిజ సమాంతరంతో 60° కోణం చేస్తూ 800 m/sతొలి వేగంతో ఒక ప్రక్షేపకాన్ని పేల్చారు.
i) భూమికి తాకే ముందు ప్రక్షేపకం ప్రయాణ కాలం కనుక్కోండి.
ii) అది భూమిని తాకే ముందు ప్రయాణించిన దూరాన్ని (వ్యాప్తి) కనుక్కోండి.
iii) గరిష్ఠ ఎత్తుకు చేరుకోడానికి పట్టే ప్రయాణ కాలాన్ని కనుక్కోండి.
సాధన:
θ = 60°, u = 800m/s

ప్రశ్న 4.
భూమికి ఏటవాలుగా ప్రక్షిప్తం చేసిన కణం తన పథంలో గరిష్ఠ బిందువు దగ్గర ఉన్నప్పుడు ప్రక్షేపణ బిందువు దృష్ట్యా దాని స్థాన సదిశ పరిమాణం అది చేరుకొనే గరిష్ఠ ఎత్తుకు √2 రెట్లు ఉన్నట్లయితే ప్రక్షేపక కోణం tan^-1 (2) అని చూపండి.
సాధన:

ప్రశ్న 5.
భూమికి 20m ఎత్తున ఉన్న శిఖరంపై నుంచి వస్తువును క్షితిజ సమాంతరానికి 30° కోణంతో 30 m/s. తొలివేగంతో ప్రయోగించారు. భూమిపై దిగే ముందు క్షితిజ సమాంతరంగా వస్తువు ఎంత దూరం ప్రయాణిస్తుంది ? (g = 10 m/s²)
సాధన:
h = 20m, θ = 30° u = 30m/s
g = 10m/s²
h = – (u sin θ) t + \(\frac{1}{2}\) gt²
20 = – 30 sin 30° × t + \(\frac{1}{2}\) × 10 × t²
20 = -30 × \(\frac{1}{2}\) × t + \(\frac{1}{2}\) × 10 × t²
4 = – 3t + t²
t² – 3t – 4 = 0
(t – 4) (t + 1) = 0
t = 4 sec (లేదా) t = – 1 sec

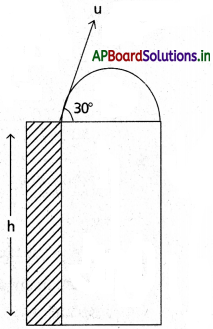
∴ వ్యాప్తి (R) = ucos θ × t
30 cos 30° × 4
= 30 × \(\frac{\sqrt{3}}{2}\) × 4
R = 60 √3 m

ప్రశ్న 6.
నేలపై 0 బిందువును మూల బిందువుగా తీసుకోవడమైంది. ఒక వస్తువు ముందు ఈశాన్య (North-East) దిశలో 102 m స్థానభ్రంశాన్ని, m ఆ తరువాత ఉత్తర దిశలో 10 m, పిమ్మట 10 √2 m వాయువ్య దిశలో పొందింది. మూల బిందువు నుంచి అది ఎంత దూరంలో ఉంది?
సాధన:
OB =10 √2 m, BC = 10m.

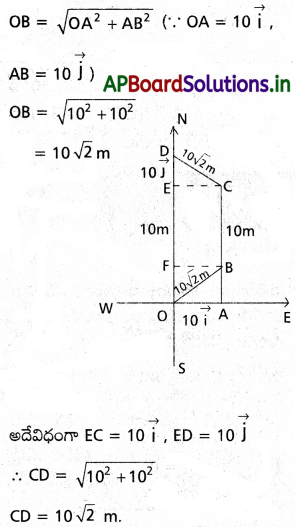
∴ మొత్తం స్థానభ్రంశం (OD) = |OF| + |FE| + |ED|
OD = 10 + 10+ 10
OD = 30m

ప్రశ్న 7.
భూమిపై ఒక బిందువు నుంచి తొలివేగం u, తో కణాన్ని క్షితిజ సమాంతర వ్యాప్తి గరిష్ఠం అయ్యే విధంగా ప్రక్షిప్తం చేశారు. దాని ఆరోహణక్రమంలో (ascent) ఉండే సగటు వేగం పరిమాణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 8.
భూమిపై నుంచి ఒక కణాన్ని కొంత తొలి వేగంతో క్షితిజ సమాంతరానికి 45° కోణంతో ప్రక్షిప్తం చేశారు. అది క్షితిజ సమాంతరంగా 10m దూరం ప్రయాణించేంతలో, భూమి నుంచి 7.5 m ఎత్తుకు చేరుతుంది. ప్రక్షేపకం తొలి వడి ఎంత? (g = 10m/s²)
సాధన:
θ = 45°, g = 10 m/s²
క్షితిజ సమాంతర దూరం (x) = 10m.
క్షితిజ లంబదూరం (y) 7.5 m.

ప్రశ్న 9.
దక్షిణ దిశ నుంచి 5 ms^-1 వేగంతో గాలి వీస్తుంది. ఒక సైకిల్ తొక్కే వ్యక్తికి అది 5ms^-1. వేగంతో తూర్పు దిశ నుంచి వీస్తుందనిపిస్తుంది. సైకిల్ తొక్కే వ్యక్తి ఈశాన్య దిశలో 5√2 ms^-1 వేగంతో ప్రయాణిస్తున్నాడని చూపించండి.
సాధన:

ప్రశ్న 10.
4 m/s తో నడుస్తున్న మనిషి వాన బిందువులు ఏటవాలుగా తన ముఖంపై 4 m/s వడితోనిట్టనిలువుతో 30°కోణం చేస్తూ పడుతున్నాయని గమనించాడు. వాన బిందువు వాస్తవ వడి 4 m/s అని చూపండి.
సాధన:
వ్యక్తి యొక్క వేగం (v_p) = 4 m/s,
v = 4 m/s, θ = 30°
సాపేక్ష వేగం (v) = v_r – v_p

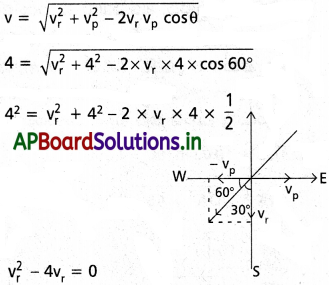
వర్షపు చినుకు వేగం (v_r) = 4m/s.

అదనపు లెక్కలు (Additional Problems)

ప్రశ్న 1.
క్రింద ఇచ్చిన రాశులు సదిశలా లేదా అదిశలా తెలపండి. ఘనపరిమాణం, ద్రవ్యరాశి, వడి, త్వరణం, సాంద్రత, మోల్ల సంఖ్య, వేగం, కోణీయ పౌనఃపున్యం, స్థానభ్రంశం, కోణీయ వేగం.
జవాబు:
అదిశ రాశులు :
ఘనపరిమాణం, ద్రవ్యరాశి, వడి, సాంద్రత, మోల్స్ సంఖ్య, కోణీయ పౌనఃపున్యం

సదిశ రాశులు :
త్వరణం, వేగం, స్థానభ్రంశం, కోణీయ వేగం

ప్రశ్న 2.
క్రింద ఇచ్చిన జాబితాలో రెండు అదిశరాశులను ఎంపిక చేయండి. బలం, కోణీయ ద్రవ్యవేగం, పని, విద్యుత్ ప్రవాహం, రేఖీయ ద్రవ్యవేగం, విద్యుత్ క్షేత్రం, సగటు వేగం, అయస్కాంత భ్రామకం, సాపేక్ష వేగం.
జవాబు:
పని మరియు విద్యుత్ ప్రవాహం ఆదిశ రాశులు

ప్రశ్న 3.
క్రింద ఇచ్చిన జాబితాలో సదిశరాశి ఉన్నది. దానిని ఎంపిక చేయండి. ఉష్ణోగ్రత, పీడనం, ప్రచోదనం, కాలం, సామర్థ్యం, మొత్తం పథం పొడవు, శక్తి గురుత్వ పొటెన్షియల్ ఘర్షణ గుణకం, విద్యుదావేశం.
జవాబు:
ప్రచోదనం = బలం × కాలం = ద్రవ్య వేగంలో మార్పు. ద్రవ్యవేగం మరియు బలం సదిశ రాశులు కావున ప్రబోదనం కూడా సదిశరాశి.

ప్రశ్న 4.
క్రింద ఇచ్చిన సదిశ, అదిశ రాశుల మధ్య జరిగే బీజగణిత పరిక్రియలు అర్థవంతమైనవో, కావో కారణాలతో వివరించండి.
a) ఏవైనా రెండు అదిశల సంకలనం,
b) ఒకే మితులు ఉన్న అదిశను సదిశకు సంకలనం చేయడం,
c) ఏదైనా సదిశను ‘ఏదైనా అదిశతో గుణించడం,
d) ఏవైనా రెండు అదిశలను గుణించడం,
e) ఏవైనా రెండు సదిశలను సంకలనం చేయడం,
f) ఒక సదిశ అంశాన్ని అదే సదిశకు సంకలనం చేయడం.
జవాబు:
a) కాదు, ఒకే మితులు గల అదిశలు కూడబడినవి.
b) కాదు, అదిశను, సదిశలో కూడరాదు.
c) అవును. త్వరణం \(\overrightarrow{A}\) ను ద్రవ్యరాశి m తో గుణించగా, బలం \(\overrightarrow{F}\) = m \(\overrightarrow{A}\) ఇది అర్థవంతమైన సమీకరణం.
d) అవును, సామర్థ్యం Pని కాలం t తో గుణించగా, పని = Pt ఇది కూడా అర్థవంతమైనది.
e) కాదు. కారణం రెండు సదిశలు ఒకే మితులు కలవి కూడబడినది.
f) అవును, కారణం రెండు సదిశలు ఒకే మితులు కలవు.

ప్రశ్న 5.
క్రింద ఇచ్చిన ప్రవచనాలను జాగ్రత్తగా చదివి కారణాలతో అవి తప్పా లేదా ఒప్పా తెలియ చేయండి.
a) సదిశ పరిమాణం ఎప్పుడూ అదిశే, b) సదిశ ప్రతీ అంశం ఎప్పుడూ అదితే, c) మొత్తం పథకం పొడవు ఎప్పుడూ కణం స్థానభ్రంశ సదిశ పరిమాణానికి సమానం, d) కణం సగటు వడి (మొత్తం పథ దూరాన్ని ఆ పథాన్ని పూర్తి చేయడానికి పట్టే కాలంతో భాగించగా వచ్చే రాశి) అదే కాలవ్యవధిలో కణం సగటు వేగం పరిమాణం కంటే ఎక్కువ లేదా సమానంగా ఉంటుంది. e) ఒకే తలంలో లేని మూడు సదిశలు కలిసి ఎప్పుడూ శూన్య సదిశను ఇవ్వలేవు.
జవాబు:
a) ఒప్పు : కారణం పరిమాణం స్వచ్ఛమైన సంఖ్య
b) తప్పు : సదిశ ప్రతి అంశము సదిశ
c) ఒప్పు : కణం సరళ రేఖా మార్గంలో ఒకేదిశలో చలిస్తోన్నప్పుడు మాత్రమే, కాకపోతే తప్పు.
d) ఒప్పు : మొత్తం పధం పొడవు, స్థాన భ్రంశంకన్నా ఎక్కువ లేదా సమానం.
e) ఒప్పు : తిభుజం యొక్క మూడు భుజాలను ఒకే దిశలో చూడలేదు.

ప్రశ్న 6.
రేఖాచిత్ర పట పద్ధతి లేదా ఇతర పద్ధతిలో క్రింద ఇచ్చిన సదిశా అసమానతలను రుజువు చేయండి.
(a) |a + b| ≤ |a| + |b| (b) |a + b| ≥ ||a|-|b||
(c) la – b|< |a! + |b| (d) |a – b| 2 ||a| – |b||
ఏ సందర్భంలో సమానత గుర్తు వర్తిస్తుంది?
జవాబు:
\(\overrightarrow{A}\) మరియు \(\overrightarrow{B}\) సదిశలు, సమాంతర చతుర్భుజం యొక్క \(\overrightarrow{OP}\) మరియు \(\overrightarrow{OQ}\) భుజాలను సూచిస్తున్నాయి.

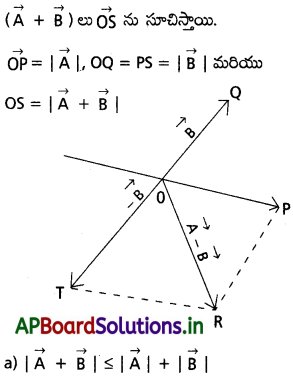
త్రిభుజం యొక్క ఒక భుజం పొడవు, మిగిలిన రెండు భుజాల పొడవులకన్నా మొత్తం కన్నా తక్కువ. AOPS, నుండి OS < OP + PS (లేదా) OS < OP + OQ

(OP – OQ) పరిమాణంను తీసుకోవాలి. కారణం
L.H.S ఎల్లప్పుడూ ధనాత్మకం కాని R.H.S రుణాత్మకం OP < PS

(iii) నుండి

రెండు సదిశలు ఒకే సరళరేఖపై పనిచేస్తున్నాయి. కాని వేరు వేరు దిశలు

∆_leOPR నుండి, OR + PR > OP (లేదా) OR > |OP – PR| (లేదా) OR > |OP – OT| ………. (viii)
(OP – OT) ధనాత్మకం, R.H.S. రుణాత్మకం, OP < OT

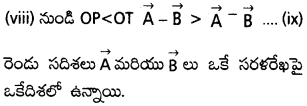
ప్రశ్న 7.
a + b + c + d = 0 అని ఇచ్చారు. కింది ప్రవచనాలలో ఏది సరియైనది?
a) a, b, c, d లలో ప్రతీది శూన్య సదిశ.
b) (a + c) పరిమాణం (b + d) పరిమాణానికి సమానం.
c) సదిశ a పరిమాణం ఎప్పుడూ b, c, d e మొత్తం పరిమాణం కంటే అధికం కాదు.
d) a, d లు ఏక రేఖీయాలు (not collinear) కానప్పుడు b + c, a, d ఉండే తలంలోనే ఉండాలి. అవి ఏక రేఖీయాలు అయితే a, d లకు రేఖీయంగా ఉండాలి.
జవాబు:

ప్రశ్న 8.
ముగ్గురు బాలికలు 200 m వృత్తాకార మంచు ఆటస్థలంలో ఆటస్థలం అంచు వెంబడి ఉన్న P బిందువు నుంచి స్కేటింగ్ చేసుకుంటూ బయలుదేరి pకి వ్యాసీయంగా (diametrically) ఎదురుగా ఉన్న Q బిందువు వద్దకు వేరు వేరు మార్గాలలో పటంలో చూపిన విధంగా చేరుకొన్నారు. ప్రతి ఒక్కరి స్థానభ్రంశం సదిశ పరిమాణం ఎంత ?. ఇది ఏ బాలిక తీసుకొన్న మార్గం పొడవుకు సమానం?

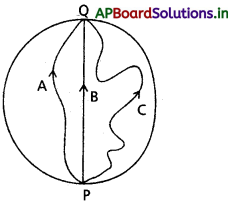
జవాబు:
ప్రతి బాలిక స్థానభ్రంశం = \(\overrightarrow{PQ}\)
ప్రతి బాలిక స్థానభ్రంశం యొక్క పరిమాణం = PQ
= గ్రౌండ్ యొక్క వ్యాసం = 2 × 200 = 400m
B బాలిక యొక్క స్థానభ్రంశం, పథం పొడవుకు సమానం.

ప్రశ్న 9.
1 km వ్యాసార్థం ఉన్న పార్క్ కేంద్రం 0 నుంచి సైకిల్పై బయలుదేరిన ఒక వ్యక్తి వృత్త అంచు Pకి చేరుకుని, వృత్త పరిధిపై సైకిల్ తొక్కుతూ తిరిగి వృత్త కేంద్రాన్ని పటంలో చూపిన OQ రేఖ వెంబడి చేరుకొన్నాడు. పూర్తి తిరుగు ప్రయాణానికి 10 నిమిషాలు తీసుకొంటే (a) ఫలిత స్థానభ్రంశం ఎంత? (b) సగటు వేగం, (c) సైకిల్ తొక్కే వ్యక్తి సగటు వడి ఎంత?

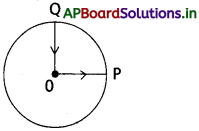
జవాబు:
a) ఇక్కడ ఫలిత స్థాన భ్రంశం = 0

ప్రశ్న 10.
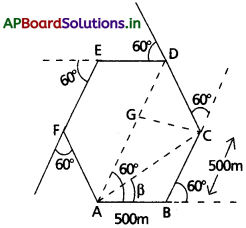
ఒక ఖాళీ ఆటస్థలంలో మోటారు సైకిల్ నడుపుతున్న వ్యక్తి ప్రతి 500m లకు అతనికి ఎడమవైపు 60° కోణంలో ఉన్న మలుపు మార్గాన్ని అనుసరిస్తున్నాడు. అతను ఉన్న మలుపు నుంచి ప్రారంభించి మోటారిస్ట్ మూడవ, ఆరవ, ఎనిమిదవ మలుపుల వద్ద అతని స్థానభ్రంశం ఎంతో చెప్పండీ? ప్రతీ సందర్భంలోనూ మోటారిస్ట్ పూర్తిచేసిన మొత్తం పథ దూరాన్ని, స్థానభ్రంశం పరిమాణంతో పోల్చండి.
జవాబు:
ఇక్కడ మార్గం షట్కోణాకారము ABCDEF పొడవు 500m. ఒక మోటారిస్ట్ Aవద్ద బయల్దేరితే

మూడవ మలుపు :
D వద్ద స్థానభ్రంశం = \(\overrightarrow{AD}\)
ఈ స్థానభ్రంశం పరిమాణం = 500 + 500 = 1000 m
A నుండి D వరకు మొత్తం పథం పొడవు = AB + BC + CD = 500 + 500 + 500 = 1500m.

ఆరవ మలుపు :
A వద్ద స్థానభ్రంశం శూన్య సదిశ. మొత్తం పథం పొడవు = AB + BC + CD + DE + EF + FA 6 × 500 3000 m.

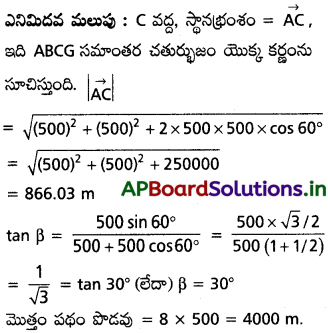
ఎనిమిదవ మలుపు :
C వద్ద, స్థానభ్రంశం = \(\overrightarrow{AC}\)
ఇది ABCG సమాంతర చతుర్భుజం యొక్క కర్ణంను సూచిస్తుంది. |\(\overrightarrow{AC}\)|
మొత్తం పథం పొడవు = 8 × 500 = 4000 m.

ప్రశ్న 11.
కొత్తగా పట్టణానికి వచ్చిన ప్రయాణీకుడు స్టేషన్ నుంచి నేరుగా ఉన్న రోడ్డుపై 10 km దూరంలో ఉండే హోటల్కు చేరుకోవాలనుకున్నాడు. మోసగాడు అయిన ఒక టాక్సీ కారుడ్రైవరు అతనిని మెలికల మార్గాల గుండా తిప్పుతూ 23 km దూరాన్ని 28 నిమిషాలపాటు తిప్పి హోటలు తీసుకొనివచ్చాడు. అయితే
(a) టాక్సీ సగటు వడ్డి ఎంత?
(b) సగటు వేగం పరిమాణం ఎంత?
(c) ఈ రెండూ సమానమేనా?
జవాబు:
ఇక్కడ మొత్తం పథం పొడవు S = 23 km,
స్థానభ్రంశం = 10 km,
కాలం t = 28 నిమిషాలు = 28/60h

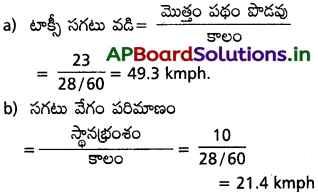
కాబట్టి సగటు వడి, సగటు వేగం సమానం కావు. ఇవి సమానం కావాలంటే టాక్సీ సరళరేఖా మార్గంలో ప్రయాణించాలి.

ప్రశ్న 12.
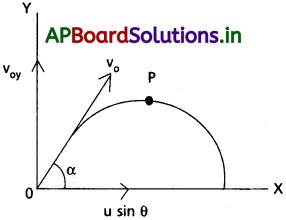
30 ms^-1 వడితో వర్షం నిట్టనిలువుగా పడుతోంది. ఒక మహిళ 10 ms^-1 వడితో ఉత్తరం నుంచి దక్షిణ దిశకు సైకిల్ను తొక్కుతోంది. ఏ దిశలో ఆమె గొడుగును పట్టుకోవాలి?
జవాబు:
పటంలో వర్షం OA దిశలో 300 ms^-1 వేగంతో పడుతోంది.
ఒక మహిళ OS దిశలో 10 ms^-1 వేగంతో పోతుంది.
OA = 30 ms^-1, OB = 10ms^-1.
ఆమె వర్షంలో తడవకుండా ఉండటానికి గొడుగును తెరిచిపట్టుకుంది. ఇప్పుడు మహిళతో పోల్చితే వర్షం సాపేక్షవేగం,
OADC సమాంతర చతుర్భుజం యొక్క కర్ణం OD అవుతుంది.

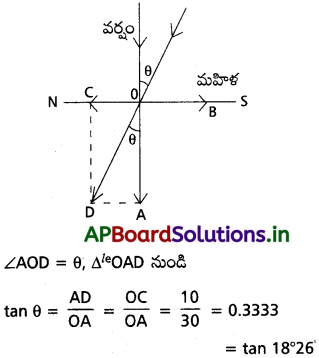
β = 18°26′ క్షితిజ లంబంతో ముందుకుపోవు దిశలో

ప్రశ్న 13.
నిలకడగా ఉన్న నీటిలో ఒక వ్యక్తి 4.0 km/h వడితో ఈదగలడు. 1.0 km వెడల్పు ఉండి 3.0 km/h సమవడితో ప్రవహిస్తున్న నదిని ప్రవాహ దిశకు లంబంగా ఈదుతూ ఎంత కాలంలో దాటగలడు? రెండో ఒడ్డుకు చేరేటప్పటికి అతడు నదిలో ఎంత కిందకు ప్రయాణిస్తాడు?
జవాబు:

ప్రశ్న 14.
ఒక నౌకాశ్రయంలో గాలి 72 km/h వడితో వీస్తుంది. నౌకాశ్రయంలో ఆగి ఉన్న నావపై ఎగురుతున్న జెండా ఈశాన్య దిశలో రెపరెప లాడుతోంది. నావ ఉత్తర దిక్కుకు 51 km/h వడితో కదలడం ప్రారంభిస్తే జెండా ఏ దిశలో ఉంటుంది?
జవాబు:
ఓడరేవులో పడవ పై ఉన్న జెండా ఉత్తర-తూర్పు దిశలలో రెపరెపలాడుతోంది. దీని అర్థం గాలిదిశ ఉత్తర- తూర్పుదిశలో ఉంది. పడవ బయల్దేరితే జెండా, పడవ పరంగా గాలి సాపేక్ష వేగం దిశలో ఊగుతోంది. \(\overrightarrow{υ}_{wt}\) అనునది పడవ పరంగా గాలి వేగం మరియు β అనునది


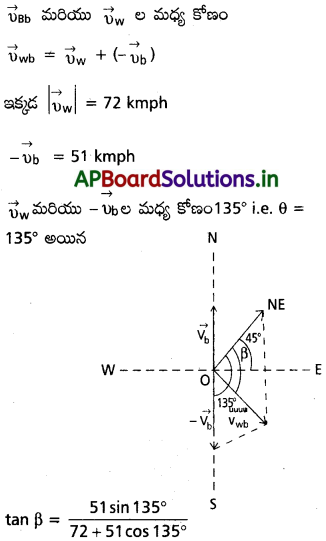
తూర్పు దిశలో కోణం = 45.1° – 45° = 0.1°
దీని అర్థం జెండా దాదాపు తూర్పు దిశలో ఎగురుతోంది.

ప్రశ్న 15.
పెద్ద హాలు లోకప్పు 25m ఎత్తు ఉంది. 40 ms^-1 వడితో విసిరిన బంతి హాలు లోకప్పును తాకకుండా వెళ్ళే గరిష్ఠ క్షితిజ సమాంతర దూరం ఎంత?
జవాబు:
ఇక్కడ u = 40 ms^-1, H = 25 m; R = ?
గరిష్ట ఎత్తు = 25 m, θ అనునది క్షితిజ సమాంతరంతో ప్రక్షిప్త కోణం

ప్రశ్న 16.
ఒక క్రికెటర్ బంతిని గరిష్ఠంగా 100m దూరం విసరగలడు. అదే బంతిని భూమికి ఎంత ఎత్తు వరకు అతడు విసరగలడు?
జవాబు:
బంతిని U వేగంతో ప్రక్షిప్తం చేశామనుకోండి. θ = 45° కోణంతో విసిరితే బంతి గరిష్ట వ్యాప్తిని పొందుతుంది.
R_max = u²/g
ఇక్కడ u²/g = 100m ……………… (i)
బంతి చలనాన్ని క్షితిజ లంబ దిశలో పరిశీలిస్తే, భూమిని కేంద్రంగా క్షితిజ లంబదిశను ధన Y-అక్షం దిశగా తీసుకుంటే
u_y = u, a_y = – g _y = 0, y₀ = 0, t = ?, y = ?
υ_y = u_y + a_yt
∴ 0 = u + (−g)t (లేదా) t = u/g

ప్రశ్న 17.
80 cm పొడవు ఉన్న తాడుకు ఒక కొన వద్ద రాయిని కట్టి స్థిర వడితో క్షితిజ సమాంతర వృత్తంలో తిప్పారు. రాయి 255 లలో 14 భ్రమణాలు చేస్తే, రాయి త్వరణం పరిమాణం, దిశను కనుక్కోండి.
జవాబు:
ఇక్కడ r = 80 cm = 0.8 m ; υ = 14/255^-1
∴ ω = 2πυ

అపకేంద్ర త్వరణం దిశ, తాడు వెంబడి వృత్తాకార పథం కేంద్రం వైపు ఉంటుంది.

ప్రశ్న 18.
ఒక విమానం స్థిర వడి 900 km/h తో 1.00km వ్యాసార్థం ఉన్న క్షితిజ సమాంతర వలయాన్ని పూర్తిచేసింది. దాని అభికేంద్ర త్వరణాన్ని గురుత్వ త్వరణంతో పోల్చండి.
జవాబు:
ఇక్కడ r = 1 km = 1000 m; υ = 900 kmph
= 900 × 1000 m × (60 × 60)^-1
= 250 m/s

ప్రశ్న 19.
కింది ప్రవచనాలను జాగ్రత్తగా చదివి తప్పొప్పుల కారణాలను ఇవ్వండి.
a) వృత్తాకార చలనంలో ఉన్న కణం ఫలిత త్వరణం ఎప్పుడూ వ్యాసార్థం వెంబడి వృత్త కేంద్రంవైపు ఉంటుంది.
b) ఏదైనా బిందవు వద్ద కణం వేగ సదిశ ఆ బిందువు వద్ద పథం స్పర్శరేఖ వెంబడి ఉంటుంది.
c) ఏకరీతి వృత్తాకార చలనంలో ఒక పూర్తి భ్రమణంలో కణం సగటు త్వరణం ఒక శూన్య సదిశ.
జవాబు:
a) తప్పు; ఏకరీతి వృత్తాకార చలనంలో మాత్రమే కణం యొక్క ఫలిత త్వరణం కేంద్రం వైపు ఉంటుంది.

b) ఒప్పు ; వృత్తాకార మార్గాన్ని వదిలినప్పుడు, కణం స్పర్శ రేఖ దిశలో చలిస్తుంది.

c) ఒప్పు ; ఏకరీతి వృత్తాకార చలనంలో కణం యొక్క త్వరణం దిశ, దాని కేంద్రం వైపు ఉంటుంది. కాలం మారినా ఇది స్థిరంగా ఉంటుంది. అన్ని సదిశల ఫలిత విలువ శూన్య సదిశ.

ప్రశ్న 20.
ఒక కణం స్థానం క్రింది విధంగా ఉంది. r = 3.0 t \(\hat{\mathbf{I}}\) – 2.0t² \(\hat{\mathbf{j}}\) + 4.0 \(\hat{\mathbf{k}}\) m ఇక్కడ t (కాలం) సెకనులో, ప్రమాణాలు మీటర్లలో ఉండే విధంగా ఇతర గుణకాల ప్రమాణాలు ఉన్నాయి. (a) కణం యొక్క v, a లను కనుక్కోండి, (b) t = 2.0 s వద్ద కణం వేగం పరిమాణం, దిశ ఏమిటి?
జవాబు:


θ = 69.5° x-అక్షం క్రింద.

ప్రశ్న 21.
మూల బిందువు t = 0 వద్ద మొదలైన కణం 10.0 \(\hat{\mathbf{j}}\) m/s వేగంతో (8.0 \(\hat{\mathbf{i}}\) + 2.0\(\hat{\mathbf{j}}\)) ms^-2 స్థిర త్వరణంతో x – y తలంపై కదులుతోంది. (a) ఏ కాలం దగ్గర కణం X -నిరూపకం 16 m అవుతుంది? అదే సమయం వద్దy-నిరూపకం ఎంత? (b) ఇదే సమయం దగ్గర కణం వడ్డి ఎంత?
జవాబు:

0 నుండి t అవధుల మధ్య వేగం u నుండి υ కి మారినది. దీనిని సమాకలనం చేయగా,

0 నుండి t అవధుల మధ్య స్థానభ్రంశం O నుండి r అయిన, సమాకలనం చేయగా

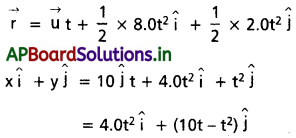
ప్రశ్న 22.

జవాబు:
మొదటి పద్ధతి :

ప్రశ్న 23.
అంతరాళంలో ఏదైనా యాదృచ్ఛిక చలనానికి కింద ఇచ్చిన ఏ సంబంధాలు ఒప్పు?
a) v_average = (1/2) (v (t₁) + v(t₂))
b) v_average = [r (t₂) – r(t₁)] / (t₂ – t₁)
c) v(t) = v(0) + a t
d) r (t) = r (0) + v(0) t + (1/2) a t²
e) a_average = [v (t₂) – v (t₁)] / (t₂ – t₁)
(ఇక్కడ ‘average’ పదం t₁ నుంచి t₂ మధ్య ఉన్న కాలవ్యవధిలో ఆయా రాశుల సగటు విలువను తెలియచేస్తుంది.)
జవాబు:
(b) మరియు (e) సంబంధాలు సరియైనవి. (a), (c) మరియు (d) సంబంధాలు సరియైనవి కాదు, కారణం కేవలం ఏకరీతి త్వరణం.

ప్రశ్న 24.
కింది ప్రవచనాలను జాగ్రత్తగా చదివి కారణాలు, ఉదాహరణలలో తప్పొప్పులను వివరించండి. అదిశ రాశి అనేది
a) ఇచ్చిన ప్రక్రియలో నిత్యత్వమయ్యేది (conserved).
b) ఎప్పుడూ రుణ విలువలను తీసుకోదు.
c) మితులు ఉండవు.
d) అంతరాళంలో ఒక బిందువు నుంచి మరొక బిందువుకు దాని విలువ మారదు.
e) పరిశీలకులు వివిధ దిగ్విన్యాసాలతో కూడిన అక్షాలలో ఉన్నా దాని విలువ ఒకే విధంగా ఉంటుంది.
జవాబు:
a) తప్పు; అస్థితిస్థాపక అభిఘాతాలలో శక్తి నిత్యత్వం కాదు.

b) తప్పు; కారణం ఉష్ణోగ్రత రుణాత్మకం.

c) తప్పు; కారణం సాంద్రతకు మితులు కలవు.

d) తప్పు; అంతరాళంలో గురుత్వ స్థితిజశక్తి బిందువు, బిందువుకు మారును.

e) ఒప్పు; అదిశరాశి విలువ అక్షాలపై ఆధారపడి మారదు.

ప్రశ్న 25.
భూమికి 3400 m ఎత్తున ఒక విమానం ఎగురుతోంది. భూమిపై ఉన్న పరిశీలన బిందువు వద్ద ఆ విమానం 10.0 s కాల వ్యవధిలో 30° కోణం చేస్తే దాని వడి ఎంత?
జవాబు:
పటంలో ౦ పరిశీలన బిందువు. A మరియు B లు విమానం స్థానాలు. ∠AOB = 30°, AB పై OC లంబాన్ని గీయాలి. ఇక్కడ OC = 3400m. ∠AOC = ∠COB = 15°. విమానం A నుండి B పోవుటకు పట్టుకాలం 10sec.

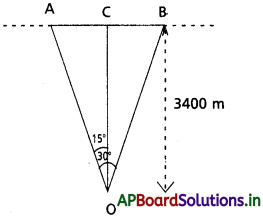
త్రిభుజం AOC నుండి, AC = OC tan 15°
= 3400 × 0.2679 = 910.86m
AC + CB = AC + AC = 2AC
= 2 × 910.86 m

ప్రశ్న 26.
ఒక సదిశకు పరిమాణం, దిశ ఉన్నాయి. దానికి అంతరాళంలో స్థానం ఉంటుందా? అది కాలంతో మారుతుందా? అంతరాళంలో వివిధ స్థానాల దగ్గర ఉన్న రెండు సమాన సదిశలు a, b లు సర్వసమాన భౌతిక ప్రభావాలను చూపించవలసిన ఆవశ్యకత ఉందా? మీ సమాధానానికి మద్దతుగా ఉదాహరణల్విండి.
జవాబు:
i) అంతరాళంలో సదిశకు సాధారణంగా ఖచ్చితమైన స్థానం ఉండదు. అందుకు కారణం అంతరాళంలో దిశ మరియు పరిమాణం మారదు. కాబట్టి సదిశ ప్రభావితం కాదు. మొత్తం మీద, స్థాన సదిశ అంతరాళంలో ఒక ఖచ్చితమైన స్థానంలో ఉంటుంది.

ii) సదిశ కాలంతో మారుతుంది. ఉదా : త్వరణం చెందే కణం వేగ సదిశ కాలంతో మారుతుంది.

iii) అంతరాళంలో రెండు సమాన సదిశలు ఒకే భౌతిక ప్రభావాలను కలిగి ఉండవు. ఉదా : రెండు సమాన బలాలు వస్తువు యొక్క రెండు వేరు వేరు బిందువుల వద్ద పనిచేస్తే ఆ వస్తువు భ్రమణం చెందుతుంది.

ప్రశ్న 27.
ఒక సదిశకు పరిమాణం, దిశ ఉన్నాయి. అంటే దిశ, పరిమాణం ఉన్న ప్రతీది సదిశ కావలసిన ఆవశ్యకత ఉందా? వస్తువు భ్రమణాన్ని దాని భ్రమణాక్షం దిశ, భ్రమణ కోణంతో వ్యక్త పరచవచ్చు. అంటే ప్రతి భ్రమణం సదిశ అవుతుందా?
జవాబు:
లేదు. కొన్ని భౌతిక రాశులకు పరిమాణం మరియు దిశ రెండూ ఉంటాయి, కాని అవి సదిశలు కావు. సదిశ సంకలన నియమాలను పాటించవు. అక్షం పరంగా వస్తువు పరిమిత భ్రమణం చెందితే, ఇది సదిశా సంకలన నియమాలను పాటించదు. వస్తువు స్వల్ప భ్రమణం చెందితే, అది సదిశ అవుతుంది. ఇది సదిశా సంకలన నియమాలను పాటిస్తుంది.

ప్రశ్న 28.
క్రింది వాటితో సదిశలను జతచేయవచ్చా? వివరించండి.
(a) ఉచ్చు (loop) ఆకారంలో వంచిన తీగ పొడవు (b) ఒక తల వైశాల్యం (c) గోళం.
జవాబు:
a) తీగను వృత్తాకారంగా వంచితే, సదిశను పొడవుకు సహచర్యం చేయలేము.

b) సమతల వైశాల్యానికి సదిశను సహచర్యం చేయ వచ్చు. దీనిని వైశాల్య సదిశ అంటారు. దీని దిశను తలానికి లంబంగా బయటకు గీస్తారు.

c) గోళం యొక్క ఘనపరిమాణానికి సదిశను సహచర్యం చేయలేము. గోళం యొక్క వైశాల్యానికి సదిశను తెలపవచ్చు.

ప్రశ్న 29.
క్షితిజ సమాంతరానికి 30° కోణంతో పేల్చిన బుల్లెట్ 3.0 km దూరంలో భూమిని తాకింది. దాని ప్రక్షేపణ కోణాన్ని సరిచేసి 5.0km దూరంలో ఉన్న లక్ష్యాన్ని గురికొట్టవచ్చని ఎవరైనా ఆశించవచ్చా? వడి స్థిరం అని, గాలి నిరోధాన్ని ఉపేక్షించడమైంది అని అనుకోండి.
జవాబు:

ప్రశ్న 30.
క్షితిజ సమాంతరంగా 1.5 km ఎత్తులో 720 km/h వడితో ఎగురుతున్న విమానం సరిగ్గా విమాన విధ్వంసక శతఘ్ని పై నుంచి వెళ్ళింది. నిట్టనిలువుతో ఏ కోణం చేస్తూ శతఘ్నిని వడి 600 ms^-1 ఉండే విధంగా పేల్చితే గుండు విమానాన్ని ఢీకొడుతుంది? శతఘ్ని నుంచి వచ్చే గుండు విమానాన్ని తాకకూడదు అంటే పైలెట్ విమానాన్ని ఎంత కనిష్ఠ ఎత్తు నుంచి తీసుకువెళ్ళాలి? (g = 10ms గా తీసుకోండి).
జవాబు:
పటంలో తుపాకి స్థానం, A అనునది విమానం స్థానం,
విమానం వేగం υ = \(\frac{720\times1000}{60\times60}\) = 200m/s
తూటా వేగం (u) = 600 m/s
t కాలం తర్వాత తూటా B వద్ద విమానంను తాకింది అనుకొనుము.
θ అనునది క్షితిజ లంబంతో కోణం t కాలంలో తూటా ప్రయాణించిన క్షితిజ సమాంతర దూరం, విమానం ప్రయాణించిన దూరానికి సమానం.
u_x × t = υt (లేదా) u sin θ t = υt

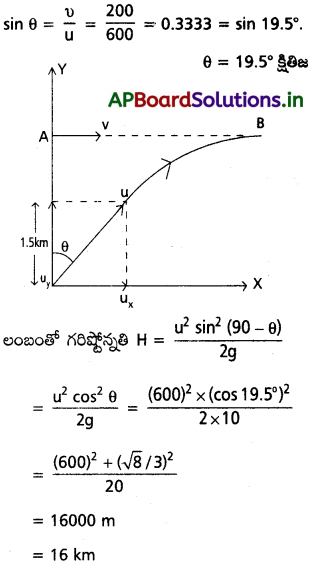
ప్రశ్న 31.
ఒక సైక్లిస్ట్ 27 km/h వడితో తొక్కుతున్నాడు. 80m వృత్తాకార వ్యాసార్థం ఉన్న వంపు ఉన్న రోడ్డును సమీపించినప్పుడు స్థిరమైన రేటుతో తన వడిని ప్రతీ సెకనుకు 0.50 m/s తగ్గేలా బ్రేకులు వేశాడు. వృత్తాకార వంపులో సైక్లిస్ట్ ఫలిత త్వరణం పరిమాణం, దిశ ఏమిటి?
జవాబు:
ఇక్కడ υ = 27 kmph = 27 × 1000 x
(60 × 60)^-1 = 7.5 ms^-1, r = 80m

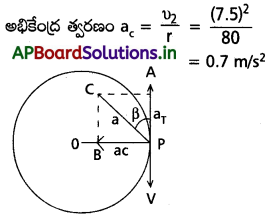
ఒక సైక్లిస్ట్ P వద్ద బ్రేకు వేస్తే, స్పర్శరేఖ త్వరణం a_T
స్పర్శరేఖ వెంబడి త్వరణం, a_T = 0.5 m/s
రెండు త్వరణాల మధ్యకోణం, 90°

ప్రశ్న 32.
a) ప్రక్షేపక వస్తువు వేగం x- అక్షానికి మధ్య ఉండే కోణాన్ని కాలం (t) ప్రమేయంగా కింది విధంగా రాయవచ్చని నిరూపించండి.

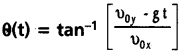
b) మూల బిందువు నుంచి ప్రయోగించిన ప్రక్షేపకం ప్రక్షేపణ కోణం కింది విధంగా ఉంటుందని నిరూపించండి.
θ ₀ = tan^-1(\(\frac{4h_{m}}{R}\))
పై సమీకరణంలో ఉపయోగించిన సంకేతాలు తమ తమ అర్థాలను కలిగి ఉన్నాయి.

జవాబు:
a) బిందువు వద్ద OX మరియు OY దిశలలో ప్రక్షేపకం తొలివేగం అంశాలు υ_ox మరియు υ_oy అనుకొనుము. ప్రక్షేపకం t కాలంలో నుండి P కి వెళ్ళినది అనుకొనుము. క్షితిజ సమాంతర మరియు క్షితిజ లంబ దిశలలో P వద్ద ప్రక్షేపకం వేగాలు υ_x, υ_y అనుకొనుము.

υ_y = υ_oy − gt మరియు υ_x = υ_ox

ఫలితవేగం \(\overrightarrow{υ}\) క్షితిజ సమాంతర దిశతో చేయు కోణం θ అనుకొనుము.

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
35 ms^-1 వడితో వాన నిట్టనిలువుగా పడుతోంది. కొంతసేపటి తరువాత 12 ms^-1 వడితో గాలి తూర్పు నుంచి పడమర దిశగా వీచడం ప్రారంభించింది. బస్టాప్లో వేచి ఉన్న బాలుడు మీద వాన పడకూడదు అంటే గొడుగును ఏ దిశలో పట్టుకోవాలి?

జవాబు:
పటంలో వాన, గాలి వేగ సదిశలను వరసగా v_r, v_w లతో సమస్యలో ఇచ్చిన దిశలో చూపించడమైంది. సదిశల సంకలన నియమం ద్వారా v_r, v_w ల ఫలిత సదిశ R పటంలో చూపిన విధంగా ఉంటుంది. R పరిమాణాన్ని కింది విధంగా లెక్కించవచ్చు.

నిట్టనిలువుతో ఫలిత సదిశ R చేసే కోణం θ ను కింది విధంగా రాయవచ్చు.
tan θ = \(\frac{v_w}{v_r}=\frac{12}{35}\) = 0.343
లేదా, θ = tan^-1(0.343) = 19°
కాబట్టి, నిట్టనిలువు తలంలో తూర్పుదిశకు 19° చేసే విధంగా గొడుగు పట్టుకొని నిలబడాలి.

ప్రశ్న 2.
సదిశలు A, B ల ఫలిత సదిశ పరిమాణం, దిశను ఆ సదిశల పరిమాణం, వాటి మధ్య కోణం θ లలో వ్యక్తపరచండి.

జవాబు:
OP, OQ రేఖలు రెండు సదిశలు A, B లను వాటి మధ్య కోణం θ తో సూచిస్తున్నాయనుకొందాం. సమాంతర చతుర్భుజ సదిశా సంకలన పద్ధతి ప్రకారం OS ఫలిత సదిశ R ను ఇస్తుంది.
R = A + B
SN, OP కి గీచిన లంబరేఖ, అలాగే OS పైకి గీచిన లంబరేఖ PM.
పటం నుంచి
OS² = ON² + SN²
కానీ ON = OP + PN = A + B cos θ
SN B sin θ
OS² = (A + B cos θ)² + (B sin θ)²
లేదా R² = A² + B² + 2AB cos θ

∆ OSN నుంచి SN = OS sin α = R sin α ∆ PSN
నుంచి SN = PS sin θ = B sin θ
కాబట్టి, R sin α = B sin θ

సమీకరణం(1) ఫలిత సదిశ పరిమాణాన్ని, సమీకరణాలు. (5), (6) లు దాని దిశను ఇస్తాయి. సమీకరణం (1) ని కొసైన్ల న్యాయం (Law of cosines) అని, సమీకరణం (4) ని సైన్ల న్యాయం (Law of sines) అంటారు.

ప్రశ్న 3.
ఒక మోటారు బోటు ఉత్తర దిశవైపు 25 km/h వేగంతో దూసుకుపోతోంది. అక్కడ నీటి సాధన. v(t) ప్రవాహం 10 km/h వేగం కలిగి దక్షిణం దిశతో 60° కోణం చేస్తూ తూర్పువైపుకు ఉంది. బోటు ఫలిత వేగాన్ని కనుక్కోండి.
జవాబు:
మోటారు బోటు వేగాన్ని v_b తో, నీటి ప్రవాహ వేగాన్ని v_c తో సమస్యలో ఇచ్చిన దిశలలో పటంలో చూపించడ మైంది. సమాంతర చతుర్భుజ సంకలన నియమం ప్రకారం ఫలిత సదిశ దిశ పటంలో చూపించిన విధంగా ఉంటుంది. కొసైన్ల న్యాయం ప్రకారం R పరిమాణాన్ని కింది విధంగా రాబట్టవచ్చు.

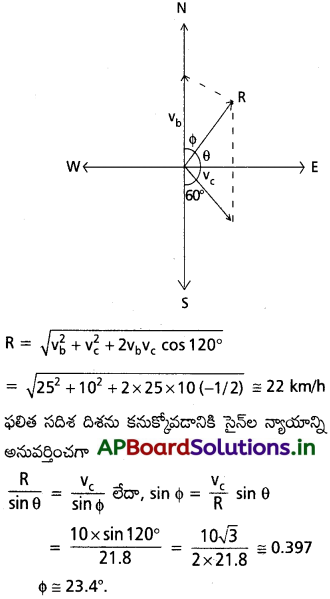
ప్రశ్న 4.
ఒక కణం స్థానాన్ని 3.ot\(\hat{\mathbf{i}}\) + 2.ot² \(\hat{\mathbf{j}}\) + 5.0\(\hat{\mathbf{k}}\) సూచిస్తుంది. ఇక్కడ t సెకనులలో, మీటర్లలో ఉండే విధంగా గుణకాలు సరైన ప్రమాణాలను కలిగి ఉన్నాయి. కణం యొక్క (a) v(t), a(t) లను కనుక్కోండి. (b) t = 1.0 s వద్ద v(t) పరిమాణం, దిశను కనుక్కోండి.
జవాబు:

ప్రశ్న 5.
కాలం t = 0 వద్ద మూల బిందువు దగ్గర నుంచి బయలుదేరిన కణం 5.0\(\hat{\mathbf{i}}\)m/s వేగంతో x-y తలంలో ప్రయోగించిన బలం వల్ల స్థిర త్వరణం (3.0\(\hat{\mathbf{i}}\) + 2.0\(\hat{\mathbf{j}}\) ) m/s² పొంది చలిస్తుంది. x – నిరూపకం 84m అయినప్పుడు కణం y– నిరూపకం ఎంత? ఈ కాలం వద్ద కణం వడి ఎంత?
జవాబు:
కణం స్థానాన్ని కింది విధంగా రాయవచ్చు.
r(t) = v_ot + \(\frac{1}{2}\) at²
= 5.0\(\hat{\mathbf{i}}\) +(1/2) (3.0\(\hat{\mathbf{i}}\) +2.0\(\hat{\mathbf{j}}\)) t²
(5.0t + 1.5t²) \(\hat{\mathbf{i}}\) + 1.0t² \(\hat{\mathbf{i}}\)
కాబట్టి, x(t) = 5.0t + 1.5 t²
y (t) = + 1.0t²
x(t) = 84m గా ఇచ్చారు. అప్పుడు t = ?
5.0 t + 1.5 t² = 84 ⇒ t = 6 s
t = 6 s అయినప్పుడు, y = 1.0 (6)² = 36.0 m

ప్రశ్న 6.
వాన నిట్టనిలువుగా 35 ms^-1. వడితో పడుతోంది. ఒక మహిళ 12ms^-1 వేగంతో తూర్పు నుంచి పశ్చిమ దిశలో సైకిల్పై వెళుతుంది. ఆమె ఏ దిశలో గొడుగును పట్టుకోవాలి?
జవాబు:
పటంలో v_r వాన వేగాన్ని v_b, మహిళ తొక్కుతున్న సైకిల్ వేగాన్ని సూచిస్తాయి. ఈ రెండు వేగాలు కూడా భూమి దృష్ట్యానే. మహిళ సైకిల్ తొక్కుతుంది. కాబట్టి, ఆమె దృష్ట్యా

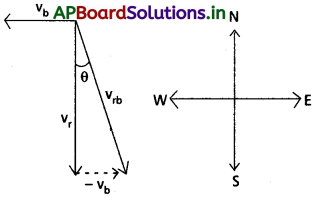
వాన వేగం, అంటే సైకిల్ వేగానికి సాపేక్షంగా వాన వేగం అని అర్థం. అంటే v_rb = v_r – V_b.
ఈ సాపేక్ష వేగం సదిశ పటంలో చూపినట్లు నిట్టనిలువుతో θ కోణం చేస్తుంది.
tan θ = \(\frac{v_b}{v_r}=\frac{12}{35}\) = 0.343
లేదా θ ≅ 19°
అంటే మహిళ పడమర దిశలో నిట్టనిలువుతో 19° కోణం చేస్తూ గొడుగును పట్టుకోవాలి.

ప్రశ్న 7.
గెలీలియో (Galileo) తన పుస్తకం Two new sciences లో ఈ విధంగా రాశాడు 45° ఇరు వైపులా సమానస్థాయిలో ఎక్కువ లేదా తక్కువ ఉన్నత అంశాల వ్యాప్తి సమానం. దీన్ని నిరూపించండి.
జవాబు:
తొలివేగం v₀ తో θ₀ కోణంతో ప్రక్షిప్తం చేసిన వస్తువు వ్యాప్తి
R = \(\frac{v_0^2 \sin 2 \theta_0}{g}\)

కోణాలు (45° + α), (45° – α), లకు θ₀ విలువ వరసగా (90° + 2α), (90° – 2α) అవుతుంది. sin (90° + 2α), sin (90° – 2α), ల విలువలు సమానం. ఆ విలువ cos 2α కు సమానం కాబట్టి ఉన్నతాంశాలు (elevations) 45° కోణానికి (సమాన స్థాయి α తో) ఎక్కువ లేదా తక్కువ అయినా వ్యాప్తులు సమానంగా ఉంటాయి.

ప్రశ్న 8.
భూమికి 490 m ఎత్తున ఉన్న శిఖరం పై నుంచి ఒక పర్వతారోహకుడు రాయిని 15ms^-1 తొలి వేగంతో క్షితిజ సమాంతరంగా విసిరాడు. గాలి నిరోధాన్ని ఉపేక్షించి, రాయి నేలను తాకేందుకు పట్టే కాలాన్ని, అది నేలను తాకే వేగాన్ని కనుక్కోండి. (g = 9.8m s^-2 గా తీసుకోండి).
జవాబు:
శిఖర శీర్షాన్ని మూల బిందువుగా తీసుకొని x, y – అక్షాలను ఊహించండి. రాయిని t = 0 s వద్ద విసిరాడు అనుకొందాం. తొలి వేగం దిశలో ధన x అక్షం దిశ, నిట్టనిలువు ఊర్ధ్వ దిశలో ధన y అక్షం దిశ ఉందను కొందాం. x−, y– చలన అంశాలను స్వతంత్ర అంశాలుగా పరిగణించవచ్చు. ఇప్పుడు చలన సమీకరణాలు :
x (t) = x₀ + υ_0xt
y (t) = y₀ + υ_0y t + (1/2) a_y t²
ఇక్కడ, x₀ = y₀ = 0, υ_0y = 0, a_y = -g = -9.8ms^-2,
υ_0x = 15 ms^-1.
y(t) = – 490 m అయినప్పుడు రాయి నేలను తాకుతుంది.
– 490 m = – (1/2) (9.8) t².
సాధించగా, t = 10 s
వేగాంశాలు υ_x = υ_0x,
υ_y = υ_0y – g t
రాయి నేలను తాకే సందర్భంలో :
υ_0x = 15 m s^-1
υ_0y= 0 – 9.8 × 10 = – 98 ms^-1
కాబట్టి, నేలను రాయి తాకే వడి

ప్రశ్న 9.
క్షితిజ సమాంతరంతో 30° కోణం చేస్తూ ఒక క్రికెట్ బంతిని 28 m s^-1 వేగంతో విసిరారు. కింది వాటిని లెక్కించండి. (a) గరిష్ఠ ఎత్తు, (b) బంతి తిరిగి అదే స్థాయికి రావడానికి పట్టే కాలం, (c) బంతి విసిరిన స్థానం నుంచి బంతి తిరిగి అదే స్థాయికి చేరిన స్థానానికి మధ్య దూరం.
జవాబు:
a) గరిష్ఠ ఎత్తు

b) బంతి తిరిగి అదే స్థాయికి రావడానికి పట్టిన కాలం
T_f = (2υ₀sin θ₀)/g = (2 × 28 × sin30°)/9.8 = 28 / 9.8 s = 2.9 s
బంతి విసిరిన స్థానం నుంచి తిరిగి అదే స్థాయికి చేరిన స్థానానికి మధ్య దూరం

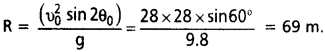
ప్రశ్న 10.
12 cm వ్యాసార్ధం ఉన్న వృత్తాకార గాడి (circular groove) లో ఇరుక్కొన్న కీటకం 100 s కాలంలో నిలకడగా 7 పరిభ్రమణాలు పూర్తి చేసింది. (a) కీటకం కోణీయ వడి; రేఖీయ వడి ఎంత? (b)త్వరణం సదిశ స్థిర సదిశేనా? దాని పరిమాణం ఎంత?
జవాబు:
ఏకరీతి వృత్తాకార చలనానికి ఇది ఒక ఉదాహరణ.
ఇక్కడ R = 12 cm. కోణీయ వడి దాని ఇలా రాయవచ్చు.
ω = 2π/T = 2π × 7/100 = 0.44 rad/s
రేఖీయ వడి υ :
υ = ωR = 0.44^-1 × 12 cm = 5.3 cm s^-1

వేగ సదిశ υ వృత్తంపై ప్రతీ బిందువు వద్ద స్పర్శరేఖ దిశలో ఉంటుంది. త్వరణం వృత్తకేంద్రం వైపు ఉంటుంది. ఇక్కడ త్వరణం దిశ నిరంతరం మారుతుంది. కాబట్టి స్థిర సదిశ కాదు. త్వరణం పరిమాణం మాత్రం స్థిరం.
a = ω²R = (0.44 s^-1)² (12 cm)
= 2.3 cm s^-2