AP Inter 1st Year Physics Study Material Chapter 9 Gravitation

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 9th Lesson Gravitation Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 9th Lesson Gravitation

Very Short Answer Questions

Question 1.
State the unit and dimension of the universal gravitational constant (G).
Answer:
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{~d}^2}\)
units of G = Nm² Kg^-2
dimensional formula of G = \(\frac{\left[\mathrm{MLT}^{-2}\right]\left[\mathrm{L}^2\right]}{[\mathrm{M}][\mathrm{M}]}\) = [M^-1 L³ T^-2]

Question 2.
State the vector form of Newtons’s law of gravitation.
Answer:
Vector form of Newton’s law of gravitation is
F = \(\frac{-G m_1 m_2}{r^3} \hat{r}\) where \(\hat{r}\) is unit vector.

Question 3.
If the gravitational force of Earth on the Moon is F, what is the gravitational force of moon on earth ? Do these forces to attraction-reaction pair ?
Answer:
F. Yes, they form action and reaction pair.

Question 4.
What would be the change in acceleration due to gravity (g) at the surface, if the radius of Earth decreases by 2% keeping the mass of Earth constant ?
Answer:
g₁r₁², l = g₂r₂², r₂ = \(\frac{98}{100}\) r₁
\(\frac{g_2}{g_1}=\frac{r_1^2}{r_2^2}=\frac{r_1^2}{\left(\frac{98}{100}\right) r_1^2}=\frac{100 \times 100}{98 \times 98}\)
\(\frac{g_2}{g_1}\) = 1.04
\(\frac{g_2}{g_1}\) – 1 = 1.04 – 1
\(\frac{g_2-g_1}{g_1}\) = 0.04

Question 5.
As we go from one planet to another, how will
a) the mass and
b) the weight of a body change ?
Answer:
a) The mass remains constant.
b) The weight (w = mg), changes from one planet to another planet.

Question 6.
Keeping the length of a simple pendulum constant, will the time period be the same on all planets ? Support your answer with reason.
Answer:
No, Time period depends on acceleration due to gravity (g).
T = 2π \(\sqrt{\frac{l}{g}}\)
g value varies from planet to planet. So time period changes.

Question 7.
Give the equation for the value of g at a depth ‘d’ from the surface of Earth. What is the value of ‘g’ at the centre of Earth ?
Answer:

1. g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) where d = Depth
   R = Radius of the Earth
2. At the centre of the Earth g = 0.

Question 8.
What are the factors that make ‘g’ the least at the equator and maximum at the poles ? > .
Answer:

1. g value is maximum at poles due to
   a) Rotation of the Earth
   b) Earth is flattened at the poles
   c) The equatorial radius is less at the poles.
2. g value minimum at equator due to
   a) Rotation of the earth
   b) Bulging near the equator.

Question 9.
“Hydrogen is in abundance around the sun but not around Earth”. Explain.
Answer:
The escape velocity on the sun is 620 km/s and escape velocity on the Earth is 11.2 km/s. The r.m.s velocities of hydrogen (2 km/s) is less than escape velocity on the Sun. So hydrogen is more abundant around the Sun and less around the Earth.

Question 10.
What is the time period of revolution of a geostationary satellite ? Does it rorate from West to East or from East to West ?
Answer:
Time period of geo-stationary satellite is 24 hours. It can rotate from west to east.

Question 11.
What are polar satellites ?
Answer:
Polar satellites are low altitude satellites (500 to 800 km), but they go around the poles of the earth in a north-south direction. Its time period is around 100 minutes.

Short Answer Questions

Question 1.
State Kepler’s laws of planetary motion.
Answer:
The three laws of Kepler can be stated as follows.

1. Law of orbits : All planets move in elliptical orbits with the sun situated at one of the foci.
   
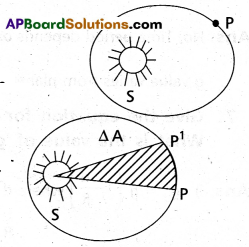
2. Law of areas : The line that joins any planet to the sun sweeps equal areas in equal intervals of time.
3. Law of periods : The square of the time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.
   T² ∝ R³

Question 2.
Derive the relation between acceleration due to gravity (g) at the surface of a planet and Gravitational constant (G).
Answer:
Consider a body of mass m on the surface of the planet. Let R be the radius of the Earth and M be the mass of the Earth.
Force acting on the body due to gravitational pull of the planet is
F = m g → (1)
According to Newton’s gravitational law, Force on the body is F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) → (2)

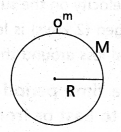
From eq’s (1) and (2), we have
m g = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\)
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
This is the relation between g and G
Mass of the earth (M) = Volume × density of the earth
M = \(\frac{4}{3}\) π R² × ρ
g = \(\frac{4}{3}\) π G R ρ

Question 3.
How does the acceleration due to gravity (g) change for the same values of height(h) and depth (d).
Answer:
a) g_h = g(1 – \(\frac{2 \mathrm{~h}}{\mathrm{R}}\)), g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
Same values of height and depth, h = d
g_h = g (1 – \(\frac{2 \mathrm{~d}}{\mathrm{R}}\)) and g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
∴ g_d > g_h

b) For large height and large depth
g_h = \(\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^2}\) and g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
If h = d = R
g_h = \(\frac{\mathrm{g}}{\left(1+\frac{\mathrm{R}}{\mathrm{R}}\right)^2}\) and g_d = g(1 – \(\frac{\mathrm{R}}{\mathrm{R}}\)) = 0
∴ g_h > g_d

Question 4.
What is orbital velocity ? Obtain an expression for it. [Mar. 14]
Answer:
Orbital velocity (V₀) : The horizontal velocity required for an object to revolve around a planet in a circular orbit is called orbital velocity.

Expression for orbital velocity :
Consider a body (satellite) of mass m, revolves round the earth in a circular orbit. Let h be the height of the satellite from the surface of the earth. Then (R + h) is the radius of the orbit.
The Gravitational force of attraction of the earth on the body is given by F = \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^2}\) ………….. (1)
Where M = Mass of the earth, R = Radius of the earth, G = universal gravitational constant. If V₀ is the orbital velocity of the body.
The centripetal force on the body is given by F = \(\frac{\mathrm{mv}_{\mathrm{o}}^2}{(\mathrm{R}+\mathrm{h})}\) …………… (2)
In order to make the body revolve in the same orbit, its centripetal force must be equal to the gravitational force

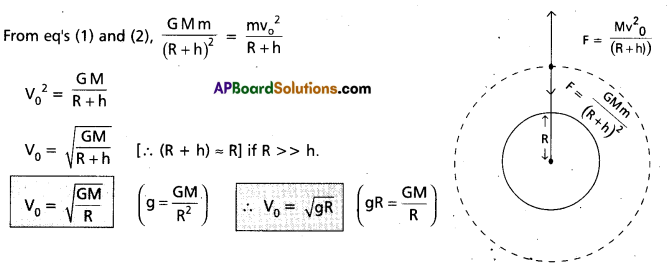
Question 5.
What is escape velocity ? Obtain an expression for it.
Answer:
Escape velocity : It is the minimum velocity with which a body should be projected, so that it moves into the space by overcoming the earth’s gravitational field.

Expression for escape velocity :
Consider a body of mass m thrown with a velocity v₂
Then K.E = \(\frac{1}{2}\) m v_e² …………. (1)
The gravitational force of attraction of the earth of mass M and Radius R on a body of mass m at its surface is F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) ……………… (2)
Gravitational P. E. = work done on the body
∴ P. E. = F × R = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) × R
P.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\) …………….. (3)
A body just escapes when its K. E. = P. E
\(\frac{1}{2}\) m v_e² = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\)
v_e² = \(\frac{2 \mathrm{GM}}{\mathrm{R}}\) (∵ g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\))
v_e = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)
v_e = \(\sqrt{2 g R}\) (gR = \(\frac{\mathrm{GM}}{\mathrm{R}}\))
v_e = \(\sqrt{2} \times \sqrt{g R}\) (∵ v₀ = \(\sqrt{g R}\))
v_e = \(\sqrt{2}\) × v₀
∴ Escape velocity is \(\sqrt{2}\) times the orbital velocity.

Question 6.
What is a geostationary satellite ? State its uses. [T.S. Mar. 18, 15; A.P. Mar. 16]
Answer:
Geo-stationary satellite : If the period of revolution of an artificial satellite is equal to the period of rotation of earth, then such a satellite is called geo-stationary satellite.
Time period of geo-stationary satellite is 24 hours.
Uses :

1. Study the upper layers of atmosphere
2. Forecast the changes in atmosphere
3. Know the shape and size of the earth.
4. Identify the minerals and natural resources present inside and on the surface of the earth.
5. Transmit the T. V. programmes to distant objects
6. Under take space research i.e. to know about the planets, satellites, comets etc.

Question 7.
If two places are at the same height from the mean sea level; One is a mountain and other is in air at which place will ‘g’ be greater ? State the reason for your answer.
Answer:
The acceleration due to gravity on mountain is greater than that of air.
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) ………….. (1)
Mass (M) = volume × density (ρ)
M = \(\frac{4}{3}\)π R³ × ρ
g = \(\frac{\mathrm{G}}{\mathrm{R}^2}\) × \(\frac{4}{3}\) π R³ ρ
g = – \(\frac{4}{3}\) π R G ρ …………….. (2)
g ∝ ρ
So density is more at mountains. So g is more on mountain.

Question 8.
The weight of an object is more at the poles than at the equator. At which of these can we get more sugar for the same weight ? State the reason for your answer.
Answer:
Weight of the object at poles = m_p g_p (∵ w = mg)
Weight of the object at equator = m_e g_e
Given weight of the object at poles > weight of the object at equator
m_p g_p > m_eg_e
We know that g_p > g_e
Then m_p < m_e
Hence we can get more sugar at equator.

Question 9.
If a nut becomes loose and gets detached form a satellite revolving around the earth, will it fall down to earth or will it revolve around earth ? Give reasons for your answer.
Answer:
When a nut is detached from a satellite revolving around the earth, the nut is also moving with the speed of the satellite as the orbit of a satellite does not depend upon its mass. Hence nut is moving in the same orbit under centripetal force.

Question 10.
An object projected with a velocity greater than or equal to 11.2 kms it will not return to earth. Explain the reason.
Answer:
The escape velocity on the surface of the earth (v_e) = 11.2 km/s. Any object projected with the velocity greater then (or) equal to 11.2 km/s it will not come back. Because it has overcome the earth’s gravitational pull.
So an object never come back to earth.

Long Answer Questions

Question 1.
Define gravitational potential energy and derive an expression for it associated with two particles of masses m₁ and m₂.
Answer:
Gravitational potential energy : Gravitational potential energy of a body at a point in a gravitational field of another body is defined as the amount of work done in brining the given body from infinity to that point without acceleration.

Expression for gravitational potential energy : Consider a gravitational field due to earth of mass M, radius R. The mass of the earth can be supposed to be concentrated at its centre 0. Let us calculate the gravitational the potential energy of the body of mass m placed at point p in the gravitational field, where OP = r and r > R. Let OA = x and AB = dx.
The gravitational force on the body at A will be
F = \(\frac{\mathrm{GMm}}{\mathrm{X}^2}\) ……………… (1)
Small amount of work done in bringing the body without acceleration through a small distance dx is given by
dw = Force × displacement
dw = F × dx
dw = \(\frac{\mathrm{GMm}}{\mathrm{X}^2}\) × dx ……………… (2)
Total work done in bringing the body from infinity to point P is given by

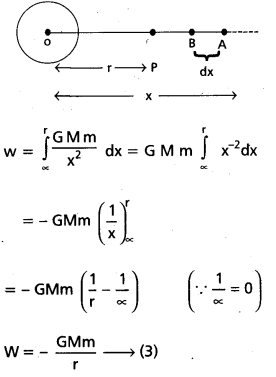
This work done is stored in the body as its gravitational potential energy (u)
∴ Gravitational potential energy (u) = \(\frac{\mathrm{GMm}}{\mathrm{r}}\) ……………….. (4)
Gravitational potential energy associated with two particles of masses m, and m2 separated by a distance r is given by
u = –\(\frac{G m_1 m_2}{r}\) ……………….. (5) (if we choose u = 0 as r → ∞).

Question 2.
Derive an expression for the variation of acceleration due to gravity (a) above and (b) below the surface of the Earth.
Answer:
i) Variation of g with height:
When an object is on the surface of the earth, it will be at a distance r = R radius of the earth, then we have g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
Where G = universal gravitational constant, M = Mass of the earth
When the object is at a height h above the surface of the earth, Then r = R + h

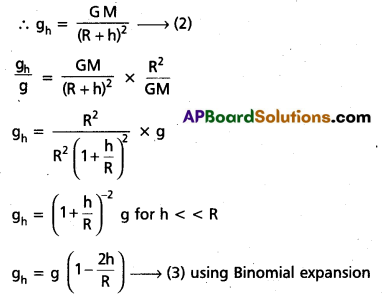
g value decreases with altitude.

ii) Variation of g with depth :
Let us assume that the earth to be a homogeneous uniform sphere of radius R, mass M and of uniform density ρ.
We know that g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) = \(\frac{4}{3}\) π ρ G R ………………… (1)
Consider a body of mass m be placed at a depth d.

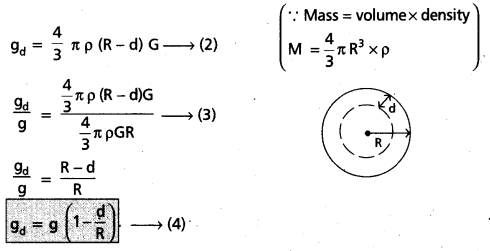
The value of g decreases with depth.

Question 3.
State Newton’s Universal Law of gravitation. Explain how the value of the Gravitational constant (G) can be determined by Cavendish method.
Answer:
Newton’s law of gravitation :
“Every body in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversly proportional to the square of the distance between them”
Determination of G value by cavendish method :

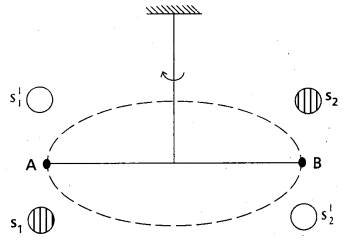
1. In 1798 Henry Cavendish determined the value of G experimentally.
2. The bar AB has two small lead spheres attached at its ends.
3. The bar is suspended from a rigid support by a fine wire.
4. Two large lead spheres are brought close to the small ones but on opposite sides as shown in figure.
5. The big spheres attract the nearby small ones by equal and opposite force as shown in figurer.
6. There is no net force on the bar but only a torque which is clearly equal to F times the length of the bar. When F is the force of attraction between a big sphere and its neighbouring small sphere.
7. Due to this torque, the suspended wire gets twisted till such time as the restoring torque of the wire equals the gravitational torque.
   Restoring torque = τ θ ………………… (1)
   Where τ is restoring couple per unit twist 0 is the angle
8. If d is the seperation between big and small balls having masses M and m.
   Gravitational force (F) = \(\frac{\mathrm{GMm}}{\mathrm{d}^2}\) ……………… (2)
   ix) If L is the length of the bar A B, then the torque arising out of F is F multiplied by L. At equilibrium, this is equal to the restoring torque.
   \(\frac{\mathrm{GMm}}{\mathrm{d}^2}\) = τ θ
   observations of θ thus enables one to calculate G.
   The measurement of G = 6.67 × 10^-11 Nm²/ Kg²

Problems

(Gravitational Constant ‘G’ = 6.67 × 10^-11 Nm²/ Kg^-2; Radius of earth ‘R’ = 6400 km; Mass of earth ‘ME’ = 6 × 10²⁴ kg)

Question 1.
Two spherical balls each of mass 1 kg are placed 1 cm apart. Find the gravitational force of attraction between them.
Solution:
m₁ = m₂ = 1 kg, d = 1 cm = 1 × 10^-2 m
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{~d}^2}\)
F = \(\frac{6.67 \times 10^{-11} \times 1 \times 1}{\left(1 \times 10^{-2}\right)^2}\) = 6.67 × 10^-7N

Question 2.
The mass of a ball is four times the mass of another ball. When these balls are separated by a distance of 10 cm, the force of gravitation between them is 6.67 × 10^-7 N. Find the masses of the two balls.
Solution:
m₁ = m, m₂ = 4m, d = 10 cm = 10 × 10^-2 m,
F = 6.67 × 10^-7 N
G = 6.67 × 10^-11 Nm²/kg ²
F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{~d}^2}\)
6.67 × 10^-7 = \(\frac{6.67 \times 10^{-11} \times \mathrm{m} \times 4 \mathrm{~m}}{\left(10 \times 10^{-2}\right)^2}\)
4 m² = 10²
m² = \(\frac{100}{4}\) = 25
m = 5 kg
∴ m₁ = m = 5 kg
m₂ = 4m = 4 × 5 = 20 kg

Question 3.
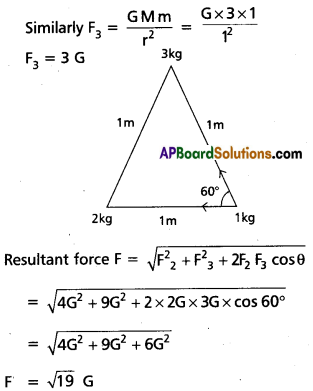
Three spherical balls of masses 1 kg, 2kg and 3 kg are placed at the corners of an equilateral triangle of side 1 m. Find the magnitude of gravitational force exerted by the 2 kg and 3kg masses on the 1 kg mass.
Solution:
The force of attraction at 2 kg on the 1 kg particle
F₂ = \(\frac{\mathrm{Gmn}{\mathrm{~d}^2}\) = \(\frac{\mathrm{G} \times 1 \times 2}{1^2}\)
F₂ = 2 G

Question 4.
At a certain height above the earth’s surface, the acceleration due to gravity is 4% of its value at the surface of earth. Determine the height.
Solution:
g_h = 4% of g = \(\frac{4}{100}\)g, R = 6400 km
g_h = \(\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^2}\)
\(\frac{4 \mathrm{~g}}{100}=\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^2}\)
\(\left(1+\frac{h}{R}\right)^2=\frac{100}{4}\) = 25
1 + \(\frac{h}{R}\) = 5
\(\frac{h}{R}\) = 4
h = 4 × R = 4 × 6400 = 25,600 km.

Question 5.
A satellite is orbiting the earth at a height of 1000km. Find its orbital speed.
Solution:
h = 1000 km
Oribital velocity (v₀) = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\)
G = 6.67 × 10^-11 Nm²/kg ², M = 6 × 10²⁴ kg
R + h = 6400 + 1000 = 7400 km
= 7400 × 10³m
v₀ = \(\sqrt{\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{7400 \times 10^3}}\)
v₀ = \(\sqrt{0.5408 \times 10^{10}}\) = 73.54 × 10³ m/s
v₀ = 7.354km/s

Question 6.
A satellite orbits the earth at a height equal to the radius of earth. Find it’s
(i) orbital speed and
(ii) Period of revolution
Solution:
Height h = R

Question 7.
The gravitational force of attraction between two objects decreases by 36% when the distance between them is increased by 4 m. Find the original distance between them.
Solution:
F₁ = F, F₂ = \(\frac{64}{100}\) F
d₁ = d, d₂ = (d + 4) m

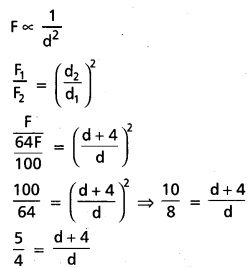
5d = 4d + 16
d = 16 m.

Question 8.
Four identical masses of m are kept at the corners of a square of side a. Find the gravitational force exerted on one of the masses by the other masses.
Solution:

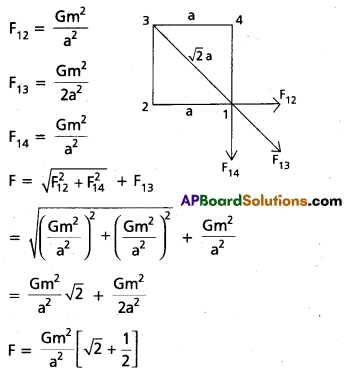
Question 9.
Two spherical balls of 1 kg and 4kg are separated by a distance of 12 cm. Find the distance of a point from the 1 kg mass at which the gravitational force on any mass becomes zero.
Solution:
m₁ = 1 kg, m₂ = 4kg, r = 12 cm
∴ x = \(\frac{r}{\sqrt{\frac{m_2}{m_1}}+1}\) from m₁
= \(\frac{12}{\sqrt{\frac{4}{1}}+1}=\frac{12}{2+1}=\frac{12}{3}\) = 4 cm
At x = 4 cm the gravitational force is zero.

Question 10.
Three uniform spheres each of mass m and radius R are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any one of the spheres due to the other two.
Solution:

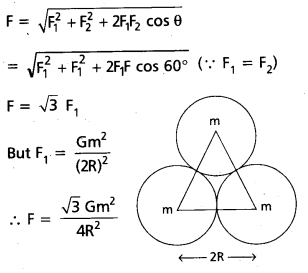
Question 11.
Two satellites are revolving round the earth at different heights. The ratio of their orbital speeds ¡s 2 : 1. If one of them is at a height of 100 km, what is the height of the other satellite ?
Solution:

4R + 400 = R + h₂
h₂ = 3R + 400 = 3 × 6400 + 400
= 19200 + 400
h₂ = 19,600 km.

Question 12.
A satellite is revolving round in a circular orbit with a speed of 8 km s-1 at a height where the value of acceleration due to gravity is 8 m s-2. How high is the satellite from the Earth’s surface ? (Radius of planet = 6000 km)
Solution:
v₀ = 8 km/s = 8000 m/s
g_h = 8 m/s², R = 6000 km = 6000 × 10³ m
∴ v₀ = \(\sqrt{\frac{G M}{R+h}}=\sqrt{g(R+h)}\)
v₀² = g(R + h)
(8000)² = 8(6000 × 10³ + h)
6000 × 10³ + h = 8 × 10⁶
h = (8 – 6) 10⁶
h = 2 × 10⁶m
h = 2000 × 10³ = 2000 km.

Question 13.
(a) Calculate the escape velocity of a body from the Earth’s surface, (b) If. the Earth were made of wood, its mass would be 10% of its current mass. What would be the escape velocity, if the Earth were made of wood ?
Solution:
R = 6400 × 10³m,

Additional Problems

Question 1.
Answer the following :
a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
b) An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity ?
c) If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the moon’s pull, (you can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the moon’s pull is greater than the tidal effect of sun. Why ?
Solution:
a) We cannot shield a body from the gravitational influence of nearby matter because the gravitational force on the body due to near by matter is independent of the presence of other matter, whereas it is not so in the case of electrical forces it means the gravitational screens are not possible.

b) Yes, if the size of the spaceship orbiting around the earth is large enough, an astronaut inside the spaceship can detect the variation in g.

c) Tidal effect depends inversly on the cube of the distance, unlike force which depends inversly on the square of the distance. Since the distance of moon from the ocean water is very small as compared to the distance of sun from the ocean water on earth. Therefore, the tidal effect of moon’s pull is greater than the tidal effect of the sun.

Question 2.
Choose the correct alternative :
a) Acceleration due to gravity increase^ decreases with increasing altitude.
b) Acceleration due to gravity increases/decreases with increas¬ing depth (assume the earth to be a sphere of uniform density).
c) Acceleration due to gravity is independent of mass of the earth/ mass of the body.
d) The formula – G Mm (1/r₂ – 1/r₁) is more/less accurate than the formula mg (r₂ – r₁) for the difference of potential energy between two points r2 and r1 distance away from the centre of the earth.
Solution:
a) decreases
b) decreases
c) mass of the body
d) more

Question 3.
Suppose there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth ?
Solution:
Here, T_e = 1 year; T_p = \(\frac{T_c}{2}=\frac{1}{2}\) year; r_e = 1
A.U.; r_p = ?
Using Kepler’s third law, we have
r_p = r_e\(\left(\frac{T_p}{T_e}\right)^{2 / 3}\) = \(1\left(\frac{1 / 2}{1}\right)^{2 / 3}\)
= 0.63 AU

Question 4.
Io, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is 4.22 × 10⁸m. Show that the mass of Jupiter is about-one-thousandth that of the sun.
Solution:
For a satellite of Jupiter, orbital period,
T₁ = 1.769 days = 1.769 × 24 × 60 × 60 s
Radius of the orbit of satellite,
r₁ = 4.22 × 10⁸ m
mass of Jupiter, M₁ is given by M₁
= \(\frac{4 \pi^2 \times\left(4.22 \times 10^8\right)^3}{G \times(1.769 \times 24 \times 60 \times 60)^2}\)
= \(\frac{4 \pi^2 r_1^3}{\mathrm{GT}_1^2}\) ……………. (1)
We know that the orbital period of earth around the sun,
T = 1 year = 365.25 × 24 × 60 × 60 s
Oribital radius, r = 1 A.U = 1.496 × 10¹¹ m

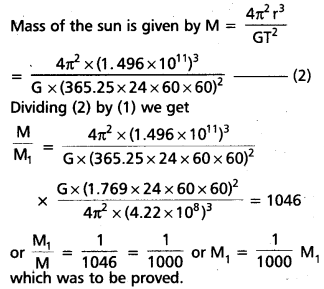
Question 5.
Let us assume that our galaxy consists of 2.5 × 10¹¹ stars each of one solar mass. How long will a star at a distance of 50,000ly from the galactic centre take to complete one revolution ? Take the diameter of the Milky Way to be 105 ly.
Solution:
Here, r = 50,000 ly =50,000 × 9.46 × 10¹⁵m
= 4.73 × 10²⁰m.
M = 2.5 × 10¹¹ solar, mass = 2.5 × 10¹¹ × (2 × 10³⁰) kg
= 5.0 × 10⁴¹ kg
We know that, M = \(\frac{4 \pi^2 r^3}{\mathrm{GT}^2}\)
or T = \(\left(\frac{4 \pi^2 r^3}{G M}\right)^{1 / 2}\)
= \(\left[\frac{4 \times(22 / 7)^2 \times\left(4.73 \times 10^{20}\right)^3}{\left(6.67 \times 10^{11}\right) \times\left(5.0 \times 10^{41}\right)}\right]^{1 / 2}\)
= 1.12 × 10¹⁶S.

Question 6.
Choose the correct alternative :
a) If the zero of potential energy is at infinity, the total energy of an orbiting satellite is negative of its kinetic/potentia! energy.
b) The energy required to launch an orbiting .satellite out of earth’s gravitational influence is more/less than the energy required to project a stationary object at the same height (as the satellite) out of earth’s influence.
Solution:
a) Kinetic energy
b) Less.

Question 7.
Does the escape speed of a body from the earth depend on (a) the mass of the body, (b) the Ideation from where it is projected, (c) the direction of projection, (d) the height of the location from where the body is launched ?
Solution:
The escape velocity is independent of mass of the body and the direction of projection it depends upon the gravitational potential at the point from where the body is launched. Since this potential depends slightly on the latitude and height of the point, therefore, the escape velocity depends slightly on these factors.

Question 8.
A comet orbits the sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit ? Neglect any mass loss of the comet when it comes very close to the Sun.
Solution:
A comet while going on elliptical orbit around the sun has constant angular momentum and total energy at all locations but other quantities vary with locations.

Question 9.
Which of the following symptoms is likely to afflict an astronaut in space
(a) swollen feet,
(b) swollen face,
(c) headache,
(d) orientational problem.
Solution:
a) We know that the legs carry the weight of the body in the normal position due to gravity pull. The astronaut in space is in weightless state. Hence, swollen feet may not affect his working.

b) In the conditions of weightless, the face of the astronaut is expected to get more supply. Due to it, the astronaut may develop swollen face. As eyes, ears, nose, mouth etc. are all embedded in the face, hence, swollen face may affect to great extent the seeing / hearing / eating / smelling capabilities of the astronaut in space.

c) Headache is due to metal strain it will persist whether a person is an astronaut in space or he is on earth it means headache will have the same effect on the astronaut in space as on a person on earth.

d) Space also has orientation. We also have the frames of reference in space. Hence, orientational problem will affect the astronaut in space.

Question 10.
In the following two exercises, choose the correct answer from among the given ones : The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig) (i) a, (ii) b, (iii) c, (iv) 0.

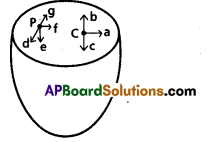
Solution:
We know that the gravitational potential is constant at all points upside a spherical shell. Therefore, the gravitational potential gradient at all points inside the spherical shell is zero [i.e as v is constant, \(\frac{\mathrm{dv}}{\mathrm{dr}}\) = 0].

Since gravitational intensity is equal to negative of the gravitational potential gradient, hence the gravitational intensity is zero at all points inside a hollow spherical shell. This indicates that the gravitational forces acting on a particle at any point inside a spherical shell, will be symmetrically placed. Therefore if we remove the upper hemispherical shell, the net gravitational forces acting on the particle at the centre Q or at some other point P will be acting downwards which will also be the direction of gravitational intensity it is so because, the gravitational intensity at a point is the gravitational force per unit mass at that point. Hence the gravitational intensity at the centre Q will be along c, i.e., option (iii) is correct.

Question 11.
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g. .
Solution:
As per explanation given in the answer of Q. 10, the direction of gravitational intensity at P will be along e i.e., option (ii) is correct.

Question 12.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero ? Mass of the sun = 2 × 10³⁰ kg, mass of the earth 6 × 10²⁴ kg. Neglect the effect of other planets etc. (orbital radius 1.5 × 10¹¹ m).
Solution:
Here M_s = 2 × 10³⁰ kg ; M_c = 6 × 10²⁴ kg ; r = 1.5 × 10¹¹ m .
Let x be the distance of a point from the earth where gravitational forces on the rocket due to sun and earth become equal and opposite. Then distance of rocket from the sun
= (r – x). If m is the mass of rocket then
\(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{m}}{(\mathrm{r}-\mathrm{x})^2}=\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{x}^2} \text { or } \frac{(\mathrm{r}-\mathrm{x})^2}{\mathrm{x}^2}=\frac{\mathrm{M}_{\mathrm{s}}}{\mathrm{M}_{\mathrm{e}}}\)

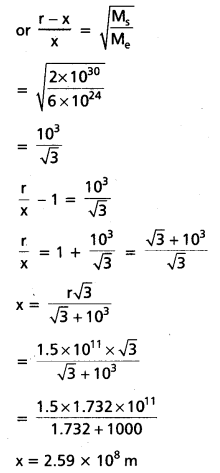
Question 13.
How will you ‘weigh the sun1, that is estimate its mass ? The mean orbital radius of the earth around the sun is 1.5 × 10⁸ km.
Solution:
To estimate the mass of the sun, we require, the time period of revolution T of one of its planets (say the earth). Let M_s, M_e be the masses of sun and earth respectively and r be the mean orbital radius of the earth around the sun. The gravitational force acting on earth due to sum is
F = \(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{M}_{\mathrm{e}}}{\mathrm{r}^2}\)
Let, the earth be moving in circular orbit around the sun, with a uniform angular velocity ω, the centripetal force acting on earth is.
F¹ = M_erω² = M_er \(\frac{4 \pi^2}{T^2}\)
As this centripetal force is provided by the gravitational pull of sun on earth, So
\(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{M}_{\mathrm{e}}}{\mathrm{r}^2}=\mathrm{M}_{\mathrm{e}} \mathrm{r} \frac{4 \pi^2}{\mathrm{~T}^2} \text { or } \mathrm{M}_{\mathrm{s}}=\frac{4 \pi^2 \mathrm{r}^3}{G \mathrm{~T}^2}\)
Knowing r and T, mass M_s of the sun can be estimated.
In this Question, we are given, r = 1.5 × 10⁸ km
= 1.5 × 10¹¹ m
T = 365 days = 365 × 24 × 60 × 60 s
∴ M_s = \(\frac{4 \times(22 / 7)^2 \times\left(1.5 \times 10^{11}\right)^3}{\left(6.67 \times 10^{-11}\right) \times(365 \times 24 \times 60 \times 60)^2}\)
= 2 × 10³⁰ kg.

Question 14.
A saturn year is 29.5 times the earth year. How far is the saturn from the sun if the earth is 1.50 × 10⁸ km away from the sun ?
Solution:
Here, T_s = 29.5 T_e; R_e = 1.5 × 10⁸ km; R_s =?
Using the relation, \(\frac{\mathrm{T}_{\mathrm{s}}^2}{\mathrm{R}_{\mathrm{s}}^3}=\frac{\mathrm{T}_{\mathrm{e}}^2}{\mathrm{R}_{\mathrm{e}}^3}\)
or R = Re \(\left(\frac{\mathrm{T}_{\mathrm{s}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\)
= 1.5 × 10⁸ \(\left(\frac{29.5 \mathrm{~T}_{\mathrm{e}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\)
= 1.43 × 10⁹ km.

Question 15.
A body weighs 63 N on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?
Solution:
Weight of the body = mg = 63N
At height h, the value of g is given by
g’ = \(\frac{g R^2}{(R+h)^2}=\frac{g R^2}{(R+R / 2)^2}\) = 4/9 g
Gravitational force on body at height h is
F = mg’ = m × \(\frac{4}{9}\) g = \(\frac{4}{9}\) mg
= \(\frac{4}{9}\) × 63 = 28N

Question 16.
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the earth if it weighed 250 N on the surface ?
Solution:
wt. of body at a depth d = mg¹
= m × g \(\left(1-\frac{d}{R}\right)\)
= 250 \(\left(1-\frac{R / 2}{R}\right)\)
= 125 N

Question 17.
A rocket is fired vertically with a speed of 5 km s^-1 from the earth’s surface. How far from the earth does the rocket go before returning to the earth ? Mass of the earth = 6.0 × 10²⁴ kg; mean radius of the earth = 6.4 × 10⁶ m; G = 6.67 × 10^-11 N m² kg^-2.
Solution:
Let the rocket be fired with velocity v from the surface of earth and it reaches a height h from the surface of earth where its velocity becomes zero.
Total energy of rocket at the surface of energy

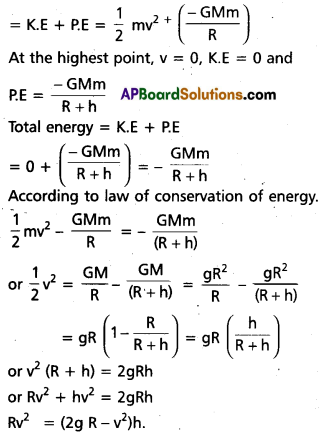
or h = \(\frac{\mathrm{Rv}^2}{2 \mathrm{gR}-\mathrm{v}^2}\)
= \(\frac{\left(6.4 \times 10^6\right) \times\left(5 \times 10^3\right)^2}{2 \times 9.8 \times\left(6.4 \times 10^6\right)-\left(5 \times 10^3\right)^2}\)
= 1.6 × 10⁶m

Question 18.
The escape speed of a projectile on the earth’s surface is 11.2 km s-1. A body is projected out with thrice this speed. What is the speed of the body far away from the earth ? Ignore the presence of the sun and other planets.
Solution:
Here, v_e = 11.2 kms^-1, velocity of projection of the body v = 3ve. Let m be the mass of the projectile and v₀ be the velocity of the projectile when far away from the earth (i.e) out of gravitational field of earth) then from the law of conservation of energy
\(\frac{1}{2}\) mv₀² = \(\frac{1}{2}\) mv² – \(\frac{1}{2}\) mv_e²
or v₀ = \(\sqrt{v^2-v_e^2}\)
= \(\sqrt{(3 v e)^2-v_e^2}\)
= \(\sqrt{8} v_e=\sqrt{8}\) × 11.2 = 31.68 kms^-1

Question 19.
A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence ? Mass of the satellite = 200 kg; mass of the earth = 6.0 × 1024 kg; radius of the earth = 6.4 × 10⁶ m; G = 6.67 × 10^-11 N m² kg^-2.
Solution:
Total energy of orbiting satellite at a hight h.
= – \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}+\frac{1}{2} \mathrm{mv}^2\)
= – \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}+\frac{1}{2} m \frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}\)
= \(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)
energy expended to rocket the satellite out of the earth’s gravitational field.
= – (total energy of orbiting satellite)
= \(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)
= \(\frac{\left(6.67 \times 10^{-11}\right) \times\left(6 \times 10^{24}\right) \times 200}{2\left(6.4 \times 10^6+4 \times 10^5\right)}\)
= 5.9 × 10⁹J

Question 20.
Two stars each of one solar mass (= 2 × 10^30< kg) are approaching each other for a head on collision. When they are a distance i09 km, their speeds are negligible. What is the speed with which they collide? The radius of each star is 10^4< km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
Solution:
Here, mass of each star, M = 2 × 10^30< kg
initial distance between two stars, r = 10^9<
km = 10^12< m.
initial potential energy of the system = – \(\frac{\text { GMM }}{r}\)
Total K.E. of the stars = \(\frac{1}{2}\) mv^2< + \(\frac{1}{2}\) mv^2<
= Mv^2<
Where v is the speed of stars with which they collide. When the stars are about to collide, the distance between their centres, r^1< = 2R.
∴ Final potential energy of two starts = \(\frac{-\mathrm{GMM}}{2 \mathrm{R}}\)
since gain in K.E. is at the cost of loss in P.E

Question 21.
Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the mid point of the line joining the centres of the spheres ? Is an object placed at that point in equilibrium ? If so, is the equilibrium stable or unstable ?
Solution:
Gravitational field at the mid – point of the line joining the centres of the two spheres.
= \(\frac{\mathrm{GM}}{(r / 2)^2}(-\hat{r})+\frac{\mathrm{GM}}{(r / 2)^2} \hat{r}=0\)
Gravitational potential at the mid point of the list joining the centres of the two spheres is
v = \(\frac{-\mathrm{GM}}{r / 2}+\left(\frac{-\mathrm{GM}}{r / 2}\right)=\frac{-4 \mathrm{GM}}{r}\)
\(\frac{-4 \times 6.67 \times 10^{-11} \times 100}{1.0}\) = -2.7 × 10^-8< J/kg
As the effective force on the body placed at mid-point is zero, so the body is in equilibrium. If the body is displaced a little towards either mass body from its equilibrium position, it will not return back to its initial position of equilibrium. Hence, the body is in unstable equilibrium.

Question 22.
As you have learnt in the text, a geo-stationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth’s gravity at the site of this satellite ? (Take the potential energy at infinity to be zero). Mass of the earth = 6.0 × 10²⁴ kg, radius = 6400 km.
Solution:
Gravitational potential at height h from the surface of earth is
v = \(\frac{-\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}\)
= \(\frac{-6.67 \times 10^{-11} \times\left(6 \times 10^{24}\right)}{\left(6.4 \times 10^6+36 \times 10^6\right)}\)
= -9.4 × 10⁶ J/kg.

Question 23.
A star 2.5 times the mass of the sun and collapsed to a size of 12 km rotates with a speed of 1.2 rev. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity ? (mass of the sun = 2 × 10^30< kg).
Solution:
The object will remain struck to the surface of star due to gravity, if the accerlation due to gravity is more than the centrifugal accerlation due to its rotation.
Accerlation due to gravity, g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
= \(\frac{6.67 \times 10^{-11} \times 2.5 \times 2 \times 10^{30}}{(12000)^2}\)
= 2.3 × 10¹² m/s²
centrifugal accerlation = rw²
= r(2πv)²
= 12000 (2π × 1.5)²
= 1.1 × 10⁶ ms^-2
since g > rω² , therefore the body will remain struck with the surface of star.

Question 24.
A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system ? Mass of the space ship = 1000 kg; mass of the sun = 2 × 10³⁰ kg; mass of mars = 6.4 × 10^23< kg; radius of mars = 3395 km; radius of the orbit of mars = 2.28 × 10^8< km; G = 6.67 × 10^-11< N m² kg ² .
Solution:
Let R, be the radius of the orbit of mars and R be the radius of the mars. M be the mass of the sun and M’ be the mass of mars. If m is the mass of the space ship, then potential energy of space-ship due to gravitational attraction of the sun = \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
potential energy of space – ship due to gravitational attraction of mars = – \(\frac{\mathrm{GM}^1 \mathrm{~m}}{\mathrm{R}^1}\)
since K.E of space ship is zero, therefore total energy of spaceship
= \(\frac{-\mathrm{GMm}}{\mathrm{R}}\) – \(\frac{\mathrm{GM}^1 \mathrm{~m}}{\mathrm{R}^1}\)
= – Gm \(\left(\frac{M}{R}+\frac{M^1}{R^1}\right)\)
∴ energy required to rocket out the spaceship from the solar system = – (total energy of space ship)

Question 25.
A rocket is fired ‘vertically’ from the surface of mars with a speed of 2 km s^-1. If 20% of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of mars before returning to it ? Mass of mars = 6.4 × 10^23< kg; radius of mars = 3395 km; G = 6.67 × 10^-11< N m² kg^-2.
Solution:
Let m = mass of the rocket, M = mass of the mars and
R = radius of mars. Let v be the initial velocity of rocket.
Initial K.E = \(\frac{1}{2}\) mv²; Initial P.E = – \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
Total initial energy = \(\frac{1}{2}\) mv² – \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
since 20% of K.E is lost, only 80% is left behind to reach the height. Therefore
Total energy available = \(\frac{80}{100} \times \frac{1}{2}\) mv²
– \(\frac{-\mathrm{GMm}}{\mathrm{R}}\) = 0.4 mv² – \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
If the rocket reaches the higher point which is at a height h from the surface of Mars, its
K.E. is zero and P.E. = \(\frac{-\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
using principle of conservation of energy, we have
0.4 mv² – \(\frac{\mathrm{GMm}}{\mathrm{R}}=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
or \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}=\frac{\mathrm{GM}}{\mathrm{R}}\) – 0.4 v²

Textual Examples

Question 1.
Let the speed of the planet at the perihelion P in Fig. be υ_p and the Sun- planet distance SP be r_p. Relate {r_p, υ_p} to the corresponding quantities at the aphelion {r_A, υ_A}. Will the planet take equal times to traverse BAC and CPB ?

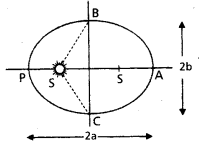
(a) An ellipse traced out by a planet around the sun. The colsest point is P and the farthest point is A. P is called the perihelion and A the aphelion. The semimajor axis (a) is half the distance AP
Answer:
The magnitude of the angular momentum at P is L_p = m_p r_p υ_p. Similarly, L_A = m_p r_A υ_A. From angular momentum conservation
m_p r_p υ_p = m_p r_A υ_A
or \(\frac{v_p}{v_A}=\frac{r_A}{r_p}\)

Question 2.
Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC. (a) What is the force acting on a mass,2m placed at the centroid O of the triangle ? (b) What is the force if the mass at the vertex A is doubled ?
Take AO = BO = CO = 1 m (see Fig)

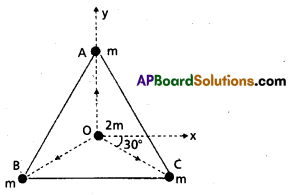
Three equal masses are placed at the three vertices of the ∆ABC. A mass 2m is placed at the centroid O.
Answer:
(a) The angle between OC and the positive x- axix is 30° and so is the angle between OB and the negative x-axis. The individual forces a vector notation are

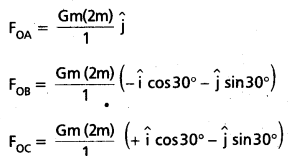
From the principle of superposition and the law of vector addition, the resultant gravitational force F_R on (2m) at O is
F_R = F_OA + F_OB + F_OC
F_R = 2Gm² \(\hat{\mathrm{j}}\) + 2Gm² \(-\hat{\mathrm{i}}\) cos 30° – \(\hat{\mathrm{j}}\) sin 30°) + 2Gm² (\(\hat{\mathrm{i}}\) cos 30° – \(\hat{\mathrm{j}}\) sin 30°) = 0
Alternatively, one expects on the basis of symmetry that the resultant force ought to be zero.

(b) By symmetry the x-component of the force cancels out. The y-component survives.
F_R = 4Gm² \(\hat{\mathrm{j}}\) – 2Gm² \(\hat{\mathrm{j}}\) = 2Gm² \(\hat{\mathrm{j}}\)

Question 3.
Find the potential energy of a system of four particles placed at the vertices of a square of side l. Also obtain the potential at the centre of the square.
Answer:
We have four mass pairs at distance l and two diagonal pairs at distance \(\sqrt{2}\)1 Hence,

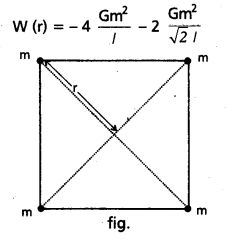
= \(\frac{2 \mathrm{Gm}}{1}\left(2+\frac{1}{\sqrt{2}}\right)\) = -5.41 \(\frac{\mathrm{Gm}^2}{l}\)
The gravitational potential U(r) at the centre of the square (r = \(\sqrt{2}\) l / 2) is
U(r) = \(-4 \sqrt{2} \frac{\mathrm{Gm}}{\mathrm{l}}\)

Question 4.
Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in Fig. The two spheres are held fixed A projeetile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.

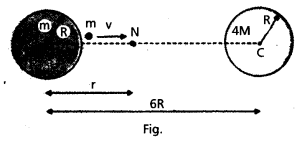
Answer:
If ON = r, we have
\(\frac{\mathrm{GMm}}{\mathrm{r}^2}=\frac{4 \mathrm{GMm}}{\left(6 \mathrm{R}-\mathrm{r}^2\right)}\)
(6R – r)² = 4r²
6R – r = ±2r
r = 2R or – 6R.
The neutral point r = -6R does not concern us in this example. Thus ON = r = 2R.
Thereafter, the greater gravitational pull of 4M would suffice. The mechanical energy at the surface of M is
E_i = \(\frac{1}{2} \mathrm{~m} v^2-\frac{\mathrm{GMm}}{\mathrm{R}}-\frac{4 \mathrm{GMm}}{5 \mathrm{R}}\)
The mechanical energy at N is purely potential.
E_N = \(-\frac{\mathrm{GMm}}{\mathrm{R}}-\frac{4 \mathrm{GMm}}{4 \mathrm{R}}\)
From the principle of conservation of mechanical energy
\(\frac{1}{2} v^2-\frac{G M}{R}-\frac{4 G M}{5 R}=-\frac{G M}{2 R}-\frac{G M}{R}\)
υ² = \(\frac{2 G M}{R}\left(\frac{4}{5}-\frac{1}{2}\right)\)
υ² = \(\left(\frac{3 \mathrm{GM}}{5 R}\right)^{1 / 2}\)

Question 5.
The planet Mars has two moons, phobos and delmos. (i) phobos has a period 7 hours, 39 minutes and an orbital radius of 9.4 × 10³ km. Calculate the mass of Mars, (ii) Assume that Earth and Mars move in circular orbits around the sun, with the Martian orbits being 1.52 times the orbital radius of the earth. What is the length of the Martain year in days ?
Answer:
(i) We employ T² = K (R_E + h)³ (where K = 4π² / GM_E) with the Earth’s mass replaced by the Martian mass M_m

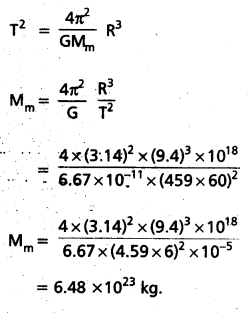
(ii) Once again Kepler’s third law comes to our aid,
\(\frac{T_M^2}{T_E^2}=\frac{R_{M S}^3}{R_{E S}^3}\)
Where R_MS is the Mars-Sun distance and R_ES is the Earth-Sun distance.
∴ T_M = (1.52)^3/2 × 365
= 684 days
For example. the ratio of the semi-minor to semi-major axis for our Earth is, b/a = 0.99986.

Question 6.
Weighing the Earth : You are given the following data g = 9.81 ms² R_E = 6.37 x106 m the distance to the moon R = 3.4 × 10⁸ m and the time period of the moons revolution is 27.3 days. Obtain the mass of the Earth M_E in two different ways.
Answer:
(1) From g = \(\frac{F}{m}=\frac{G M_E}{R_E^2}\)
M_E = \(\frac{g R_E^2}{G}\)
= \(\frac{9.81 \times\left(6.37 \times 10^6\right)^2}{6.67 \times 10^{-11}}\)
= 5.97 × 10²⁴kg. (by Method – 1)

(2) The moon is a satellite of the Earth. From the derivation of Kepler’s third law

= 6.02 × 10²⁴kg (by Method – 2)
Both methods yield almost the same answer the difference between them being less than 1%.

Question 7.
Express the constant k T² = K (R_E + h)² where K = 4π²/GM_E of in days and kilometres. Given k = 10^-13 s² m^-3. The moon is at a distance of 3.84 × 10⁵ km from the earth. Obtain its time period of revolution in days.
Answer:
Given
k = 10^-13 s² m^-3 (d = day)
= 10^-13 \(\left[\frac{1}{(24 \times 60 \times 60)^2} d^2\right]\)
\(\left[\frac{1}{(1 / 1000)^3 \mathrm{~km}^3}\right]\) = 1.33 × 10^-14 d² km^-3
Using T² = K (R_E + h)³ (where k = 4π²/ GM_E) and the given value of k the time period of the moon is
T² = (1.33 × 10^-14) (3.84 × 10⁵)³
T = 27.3 d

Question 8.
A 400 kg satellite is in a circular orbit of radius 2R_E about the Earth. How much energy is required to transfer it to a circular orbit of radius 4R_E? What are the changes in the kinetic and potential energies ?
Answer:
Initially,
E₁ = \(\)
While finally
E_f = \(\)
The change in the total energy is
∆E = E_f – E_i
= \(\frac{\mathrm{GM}_E \mathrm{~m}}{8 R_E}=\left(\frac{\mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}^2}\right) \frac{\mathrm{mR} \mathrm{R}_{\mathrm{E}}}{8}\)
∆E = \(\frac{\mathrm{gm} \mathrm{R}_{\mathrm{E}}}{8}=\frac{9.81 \times 400 \times 6.37 \times 10^6}{8}\)
= 3.13 × 10⁹J
The kinetic enegy is reduced and it mimics ∆E, namely, ∆K = K_f – K_i = -3.13 × 10⁹ J.
The change in potential energy is twice the change in the total energy, namely
∆V = V_f – V_i= -6.25 × 10⁹ J