AP Inter 2nd Year Maths 2A Important Questions Chapter 4 సమీకరణ వాదం

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 4 సమీకరణ వాదం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 4 సమీకరణ వాదం

ప్రశ్న 1.
2,3,6 లు మూలాలుగా గల 3 వ తరగతి ఏక బహంపది సమీకరణాన్ని రూపొందించండి.
సాధన:
కావలసిన బహుపది సమీకరణ
(x-2)(x-3)(x-6) = 0
⇒ x³-11 x²+36 x-36=0

ప్రశ్న 2.
3x³-10x²+7 x+10=0 ఘన సమీకరణం యొక్క మాలాలు, గుణకాల మధ్య సంబంధాలను కనుక్కోండి.
సాధన:
3x³-10x²+7x + 10 = 0 ……………. (1)
(1) ను ax³+bx²+c x+d=0 తో పోల్చగా

ప్రశ్న 3.
x⁴-2x³+4x²+6 x-21=0 ద్వివర్గ సమీకరణం యొక్క మాలాలు, గుణకాల మధ్య సంణంధాలను కనుక్కోండి.
సాధన:
దత్త సమీకరణం
x⁴-2x³+4x²+6 x-21=0
ax⁴+b x³+cx²+dx+e=0  తో పోల్చగా
a=1, b=-2, c=4, d=6, e=-21

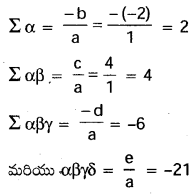
ప్రశ్న 4.
x⁴+a x³+b x²+c x+d=0 సమీకరణం మొక్క మూలాలు 1, 2, 3, 4 బయితే a, b, c, d విలువలు కనుక్కోండి.
సాధన:
దత్త సమీకరణ మూలాలు 1, 2, 3, 4
కనుక  x⁴+a x³+b x²+c x+d
≡ (x-1) (x-2) (x-3) (x-4)=0
≡ x⁴-10x³+35x²– 50x+24=0
ఇరువైపుల పదాల గుణకాలను పోల్చగా
a=-10, b=35, c=-50, d=24

ప్రశ్న 5.
సమీకరణం x³-p x²+q x-r=0 మూలాలు a,b,c ల అయి, r ≠ 0 అయితే, అప్పుడు \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\) ను p, q, r లలో కనుక్కోండి.
సాధన:
a, b, c లు
x³-p x²+q x-r=0 కు మూలాలు
a+b+c=p, a b+b c+c a=q, a b c=r

ప్రశ్న 6.
x³-p x²+q x-r=0 సమీకరణ యొక్క మాలాల వర్గాల మొత్తాన్ని, ఘనాల మెత్తాన్ని p q r  లలో కనుక్కోండి.
సాధన:

ప్రశ్న 7.
x³+p₁ x²+p₂ x+p₃=0 సమీకరణం యొక్క మూలాల వర్గాలు మూలాలాగా ఉండే ఘన సమీకరణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 8.
x³+px²+qx+r =0 మాలాలు α, β, γ లు అయితే కింది వాటిని కనుక్కోండి.
(i) ∑ a²
(ii) ∑ \(\frac{1}{\alpha}\)
(iii) ∑ a³
(iv) ∑ β² γ²
(v) (α + β) (β + γ ) (γ + α )

(i) ∑ a²
సాధన:
α² + β² +  γ²
=(α+β+γ)² -2(αβ + βγ+ γ α)
p² – 2q

(ii) ∑ \(\frac{1}{\alpha}\)
సాధన:
\(\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}=\frac{\beta \gamma+\gamma \alpha+\alpha \beta}{\alpha \beta \gamma}=\frac{-q}{r}\)

(iii) ∑ α³
సాధన:
∑ α³ 
= (α+ β + γ) (a² + β² + γ² – αβ + βγ +γα)+3αβγ
= (- p)(p² -2q – q) – 3r
= – p(p²– 3q) – 3r
∴ ∑ α³ = – p³ + 3pq – 3r = 3pq – p³– 3r

(iv) ∑ β² γ²
సాధన:

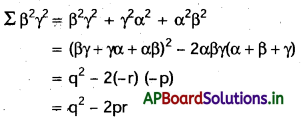
(v) (α + β) (β + γ ) (γ + α )
సాధన:
α + β + γ = – p
⇒ α + β = – p – γ మరియు β + γ = – p – α
= γ + α = – p – β
∴ (α + β) (β + γ) (γ + α)
= ( – p – γ)( – p – α) ( – p – β)
=-p³-p² (α + β + γ) – p (αβ+βγ+γα)-αβγ
= -p³ + p³-pq + r = r – pq

ప్రశ్న 9.
x³+ax²+b x+c=0 మూలాలు α,β,γ లు అయితే ను కనుక్కోండి.
సాధన:
α,β,γ లు దత్త సమీకరణం యొక్క మూలాలు కనుక
α + β + γ = – α, αβ + βγ + γα = b, αβγ = c

ప్రశ్న 10.
α,β,γ లు x³+p²+q x+r=0 మూలాలు అయితన,  లు మూలాలుగా గల ఏక ఘన సమీకరణాన్ని కనుక్కోండి.
సాధన:

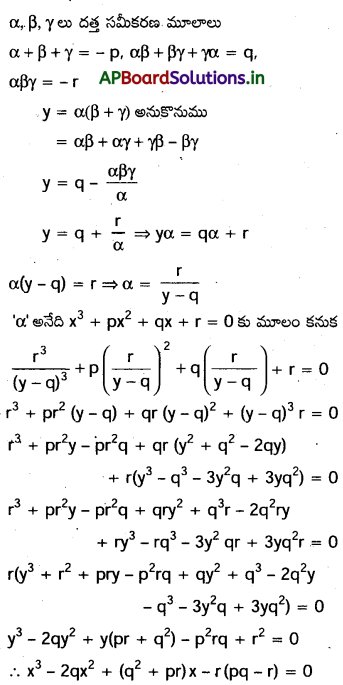
ప్రశ్న 11.
x³-3x²-16 x+48=0 ను సాధించండి.
సాధన:
f(x)=x³-3 x²-16 x+48 అనుకోండి
యత్న – దోష పద్ధతిన f(3)=0
కనుక f(x)=0 కు 3 మూలం
f(x) ను (x-3) చే భాగించగా

ప్రశ్న 12.
x⁴-16 x³+86x²-176 x+105=0 యึక్క మాలాలను కనుక్కోండి.
సాధన:

∴ g(x) & =(x-3)(x²-12 x+35)
=(x-3)(x-5)(x-7)
∴ f(x) & =(x-1)(x-3)(x-5)(x-7)
∴ దత్త సమీకరణం మూలాలు 1,3,5,7

ప్రశ్న 13.
x³-7x²+36=0 సమీకరణం మొక్క ఒక మాలం మరో దానికి రెట్టింప అయితే, సమీంరాాన్ని సాధించండి.
సాధన:
x³-7x²+36=0 కు మూలాలు α, β, γ లు అనుకోండి.
β =2α అనుకుందాం
అయిన α + β + γ = 7
⇒ 3α + γ  =7 ………….. (1)

ప్రశ్న 14.
x³-6x²+3 x+10=0 సమీకరాానికి ఒక మూలం 2 అయితే, మిగిలిన మాలాలను కనుక్కోండి.
సాధన:
f(x)=x³-6x²+3 x+10 అనుకానుము.
f(x)=0 కు 2 మూలం కనుక f(x) ను (x-2) చే భాగించగా

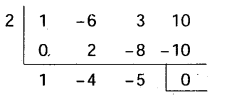
x³-6x²+3 x+10 = (x – 2)(x² – 4x – 5)
(x-2) (x+ 1) (x-5)

ప్రశ్న 15.
4x³+20x²-23 x+6=0 సమీకరణం యొక్క రెండు మూలాలు సమానమైతే, సమీకరణం యొక్క మాలాలన్నింటిని కనుక్కోండి.
సాధన:
α,β,γ లు  4x³+20x²-23 x+6=0  కు మూలాలు. రెండు మూలాలు సమానం కనుక α = β అనుకోండి.

పరిశీలనవల్ల
α = \(\frac{1}{2}\) దత్త సమీకరణానికి మూలం
(2) ⇒ γ = – 6
∴ దత్త సమీకరణం మూలాలు \(\frac{1}{2}, \frac{1}{2},-6\)

ప్రశ్న 16.
x⁴– 2x³+4x³+6 x-21=0 సమీకరణం మొక్కరెండు మూలాల మొత్తం సున్న అయితే, సమీకరణ మొక్క మూలాలను కనుక్కోండి.
సాధన:
α, β, γ, δ లు దత్త సమీకరణ మూలాలు,
రెండు మూలాల మొత్తం సున్నీ కనుక
α + β = 0 అనుకొనుము.

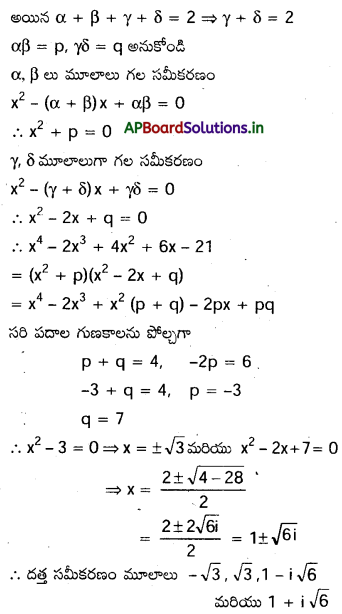
ప్రశ్న 17.
4x³-24x²+23x+18=0 సమీకరణం యొక్క మూలాలు అంకశేఢిలో ఉంటీ, సమీంరణాన్ని సాధించండి.
సాధన:
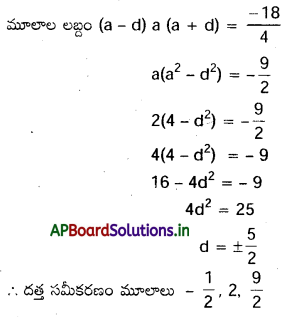
a – d, a, a + d లు దత్త సమీకరణ మూలాలు అనుకోండి మూలాల మొత్తం
a – d + a + a + d = \(\frac{24}{4}\)
3a = 6
a = 2

ప్రశ్న 18.
x³-7x²+14x-8=0, సమీకరణం మూలాలు గుణరీశేధిలో ఉంటే, సమీకరణాన్ని సాధించండి.
సాధన:
దత్త సమీకరణం మూలాలు \(\frac{a}{r}\), a, అనుకుందాం. అప్పుడు

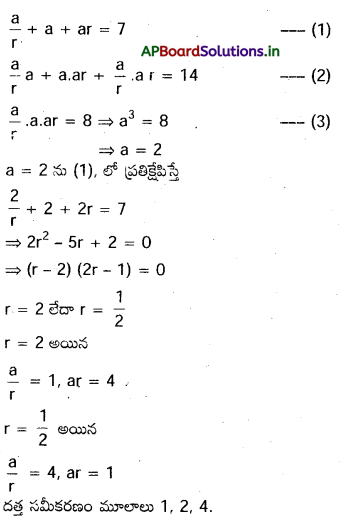
ప్రశ్న 19.
x⁴-5x³+5x³+5 x-6=0 సమీకరణం మొక్క రెండు మూలాల లబ్దం 3 అయితే ఆ సమీకరణాన్ని సాధించండి.
సాధన:
α, β, γ, δ లు మూలాలు అనుకుంటే.
వాటి లబ్దం αβγδ =-6
αβ=3 ( రెండు మూలాల లబ్దం 3)
∴ αβγδ = -6
γδ = – 2
α +β = p, γ, δ + q అనుకోండి
αβ లు మూలాలుగా గల సమీకరణం
x²-(α +β) x + αβ =0
x²-p x+3=0
γ ,δ లు మూలాలుగా గల సమీకరణం
x² – (γ + δ)x + γδ = 0
x² – qx – 2 = 0
x⁴ – 5x³ + 5x² + 5x – 6
= (x²-px-t- 3)(x²– qx – 2)
= x⁴ – (p + q) x³ + (1 + pq) x² +(2p-3q)x-6
సరిపదాల గుణకాలను పోల్చగా
p+q=5, 2p-3 q=5
∴ 2 p-3 q=5
3 p+3 q=15
5 p=20 ⇒ p=4
∴ q = 1
x² -4x+3=0 ⇒ (x-3)(x-1)=0
⇒ x=1,3
x²-x-2=0 ⇒ (x-2)(x+1)=0
⇒ x = -1,2
∴ దత్త సమీకరణం మూలాలు -1,2,1,3

ప్రశ్న 20.
x⁴+4x³-2x²-12x+9=0 సమీకరణానికి రంండు జతల సమాన మూలాలు ఉంటే, సమీకరణాన్ని సాధించండి.
సాధన:

x² + 2x+p = 0 = x²+2x – 3 = 0
⇒ (x-1-3) (x – 1) = 0
⇒ x = – 3,1
దత్త సమీకరణం మూలాలు -3, – 3, 1 ,1

ప్రశ్న 21.
p³ – 4 p q+8 r=0 అయితేనే x⁴+px³+q x² + rx+s=0 మొక్క రెండు మాలాల మొత్తం మిగిలిన రెండు మూలాల మొత్తానికి సమానమని నిరూపించండి.
సాధన:
దత్త సమీకరణం రెండు మూలాల మొత్తం మిగిలిన రెండు మూలాల మొత్తానికి సకానమని అనుకుందాం. α β γ δ అయ్యేటట్లు సమీకరణం మూలాలను α + β = γ + δ అనుకుందాం.

ప్రశ్న 22.
\(4+\sqrt{3}, 4-\sqrt{3}, 2+i, 2-i\) లను మాలాలుగా గల 4వ తరగతి ఏక ఱహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
\(4+\sqrt{3}, 4-\sqrt{3}\) లు మూలాలుగా గల సమీకరణం
2+i, 2 – i లు మూలాలుగా గల సమీకరణం
x²-4 x+5=0
కావలసిన సమీకరణం
(x²-8 x+13)(x²-4 x+5)=0
∴ x⁴-12x³+50x²-92 x+65=0

ప్రశ్న 23.
6x⁴-13 x³-35 x²-x+3=0 సమీకరణం యొక్క ఒక మూలం. \(2+\sqrt{3}\) అయితే సమీకరణాన్ని సాధించండి.
సాధన:

ప్రశ్న 24.
x⁴-6 x³+7x²-2 x+1=0 సమీకరణం మొక్క మూలాల వ్యతిరేక గుర్తులతో మాలాలు గల నాలుగో తరగతి ణహబపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
f(x) ≡  x⁴-6x³+7x²-2 x+1=0
కావలసిన సమీకరణం f(-x)=0
i.e., (-x)⁴-6(-x)³+7(-x)²-2(-x)+1=0
∴ x⁴+6x³+7x²+2x+1=0

ప్రశ్న 25.
6x⁴-7x³+8x²-7x+2=0 సమీకరణం మొక్క మాలాలకు 3 రెట్లున్న మాలాలు గల నాలుగో తరగతి బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
f(x) ≡ 6x⁴-7x³+8x²-7 x+2=0

ప్రశ్న 26.
\(x^3+\frac{x^2}{4}-\frac{x}{16}+\frac{1}{72}\) = 0 సమీకరణ మూలాలకు m రెట్లున్న మూలాలు గల మూడో తరగతి సమీకరణాన్ని రూపొందించి, m = 12 సందర్భానికి సమీకరణాన్ని రాణట్టండి.
సాధన:

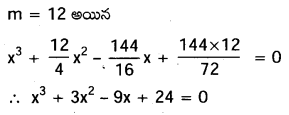
ప్రశ్న 27.
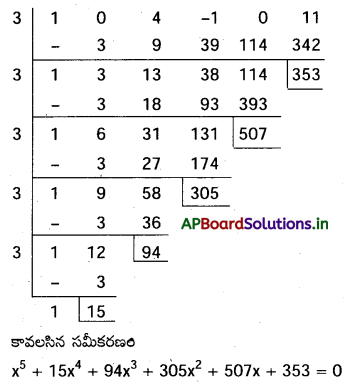
x⁵+4 x³-x²+11=0 సమీకరణ మూలాలు -3 తో మార్పు చెందగా వచ్చే విలువలను మూలాలుగా కలిగిన 5వ తరగతి ణహంపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
f ≡ x⁵+4 x³-x²+11=0
కావలసిన సమీకరణం f(x+3)=0

ప్రశ్న 28.
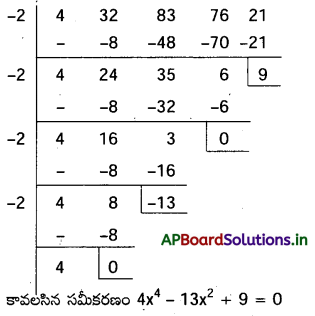
4x⁴+32x³+83x²+76 x+21=0 మూలాలు 2 తో మార్పు చెందగా వచ్చే విలువలను మాలాలుగా గల 4 వ తరగతి బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
f(x) ≡ 4x⁴+32x³+83x²+76 x+21=0
కావలసిన సమీకరణం f(x-2)=0

ప్రశ్న 29.
x⁴+3x³-6 x²+2 x-4=0 సమీకరణ మాలాల వ్వత్కమ్మాలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:

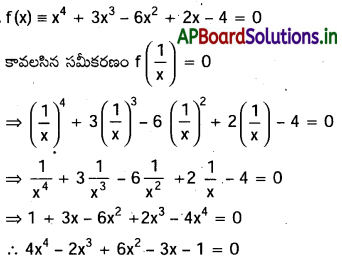
ప్రశ్న 30.
x³-x³+8 x-6=0 మాలాల వర్గాలు మాలాలుగా గల ఐహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 31.
2x³+5x²+5 x+2=0 ఒకటో కోవకు చెందిన వ్కత్రమ సమీకరణమని చూపండి.
సాధన:
దత్త సమీకరణం 2x³+5x²+5 x+2=0
P₀ =2, P₁ =5, P₂ =5, P₃ =2
ఇచ్చట P₀ = P₃, P₁ = P₂
∴ 2x³+5x²+5 x+2=0 సమీకరణం ఒకటో కోవకు చెందిన వ్యుత్రమ సమీకరణం.

ప్రశ్న 32.
సాధించండి : 4x³-13x²-13 x+4=0
సాధన:
4x³-13x²-13x+4=0
ఒకటో కోవకు చెందిన బేసి పరిమాణ వ్యుత్కమమ సమీకరణం కనుక -1 దీనికి ఒక మూలం

4x²-17 x+4=0 4x²-16 x-x+4=0
4x(x-4)-1(x-4)=0
(x-4)(4 x-1)=0
x=4 (లేదా) \(\frac{1}{4}\)
∴ దత్త సమీకరణం మూలాలు -1,4, \(\frac{1}{4}\)

ప్రశ్న 33.
సాధించండి :
6x⁴-35x³+62x²-35 x+6=0
సాధన:
6x⁴-35x³+62x²-35 x+6=0

ప్రశ్న 34.
సాధించండ: :
x⁵-5x⁴+9x³-9x²+5 x-1=0
సాధన:
దత్త సమీకరణం
x⁵-5x⁴+9x³-9x²+5 x-1=0 రండో కోవకు చెందిన బేసి పరిమాణ వ్రుత్రమ సమీకరణం

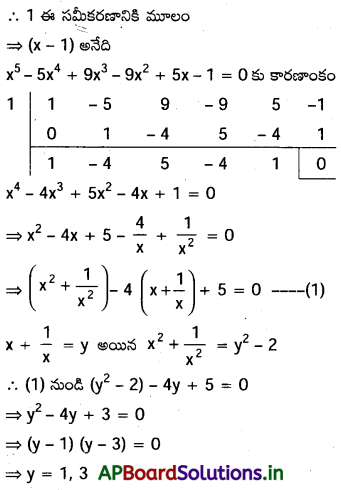
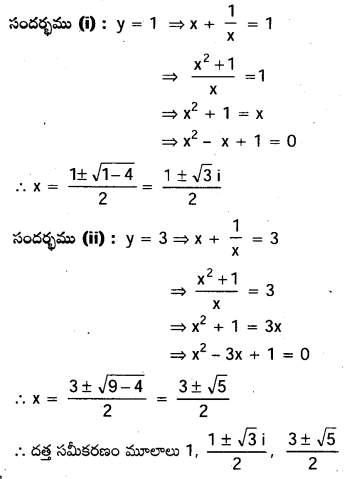
ప్రశ్న 35.
సాధించండి :
6x⁶-25x⁵+31x⁴-31x²+25 x-6=0
సాధన:
దత్త సమీకరణం
6x⁶-25x⁵+3 x⁴-31x²+25 x-6=0 ఇది రెండవ కోవకు చెందిన సరి పరిమాణ వ్యుత్కమ సమీకరణం
∴ x² -1 అనేది