AP Inter 1st Year Chemistry Study Material Chapter 4 పదార్ధం స్థితులు : వాయువులు, ద్రవాలు

Andhra Pradesh BIEAP AP Inter 1st Year Chemistry Study Material 4th Lesson పదార్ధం స్థితులు : వాయువులు, ద్రవాలు Textbook Questions and Answers.

AP Inter 1st Year Chemistry Study Material 4th Lesson పదార్ధం స్థితులు : వాయువులు, ద్రవాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాయు అణువుల మధ్య ఉండే వివిధ రకాల అంతరఅణుబలాలను పేర్కొనండి.
జవాబు:
విక్షేపణ బలాలు, ద్విధృవ – ద్విధృవ ఆకర్షణ బలాలు, ద్విధృవ – ప్రేరిత ద్విధృవ బలాలు, హైడ్రోజన్ బంధం మొ||నవి అంతరఅణుబలాలు.

ప్రశ్న 2.
బాయిల్ నియమాన్ని తెలిపి, దాని గణితాత్మక రూపం తెలపండి.
జవాబు:
బాయిల్ నియమం : స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి ఉన్న వాయువు ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది.
V ∝ \(\frac{1}{P}\)
V = వాయు ఘనపరిమాణం
P = వాయు పీడనం

ప్రశ్న 3.
ఛార్లెస్ నియమాన్ని తెలిపి, దాని గణితాత్మక రూపం తెలపండి.
జవాబు:
ఛార్లెస్ నియమం :
స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం ప్రతి 1°C ఉష్ణోగ్రత పెరుగుదలకు 0° C వద్ద దాని ఘనపరిమాణంలో \(\frac{1}{273}\) పెరుగుతుంది.
V_t = V₀ (1 + \(\frac{t}{273}\))

నియమిత భారం గల వాయువు ఘనపరిమాణం స్థిరపీడనం వద్ద దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.
P ∝ T లేదా \(\frac{P}{T}\) = స్థిరాంకం ;
అనగా \(\frac{P_1}{T_1}=\frac{P_2}{T_2}\)

ప్రశ్న 4.
సమోష్ణోగ్రతరేఖలు (Isotherms) అంటే ఏమిటి ?
జవాబు:
ఒక వాయువు స్థిర ఉష్ణోగ్రత వద్ద ఘనపరిమాణాన్ని X – అక్షం మీద పీడనాన్ని Y – అక్షం మీద తీసుకుని గ్రాఫ్ గీయగా ఒక చతురస్రాకార పరావలయం లభిస్తుంది. ఇది స్థిర ఉష్ణోగ్రత వద్ద, నిర్ణీత భారం గల వాయువుకు P, V ల మధ్య సంబంధాన్ని తెలుపుతుంది. దీనినే సమోష్ణోగ్రతా రేఖ అంటారు.

ప్రశ్న 5.
పరమ ఉష్ణోగ్రత అంటే ఏమిటి?
జవాబు:
దీనినే కెల్విన్ ఉష్ణోగ్రత అంటారు. ఏ ఉష్ణోగ్రత వద్దనైతే పరమ (లేదా) కెల్విన్ స్కేల్ సున్నా – 273.16° C వద్ద ఉంటుందో దానినే పరమ ఉష్ణోగ్రత అంటారు.

ప్రశ్న 6.
సమపీడన రేఖలు (lsobars) అంటే ఏమిటి?
జవాబు:
స్థిర పీడనం వద్ద గీయు గ్రాఫ్లను సమపీడన రేఖలు (Isobars) అంటారు.
ఉదా : ఘనపరిమాణం, ఉష్ణోగ్రత మధ్య గీయు గ్రాఫు.

ప్రశ్న 7.
పరమశూన్య ఉష్ణోగ్రత అంటే ఏమిటి?
జవాబు:

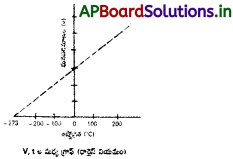
వాయు ఘనపరిమాణానికి, ఉష్ణోగ్రతకు సంబంధించిన గ్రాఫ్ ప్రకారం – 273°C వద్ద ప్రతి వాయువు ఘనపరిమాణం సున్న అవుతుంది. ఈ ఉష్ణోగ్రతను పరమశూన్య ఉష్ణోగ్రత అంటారు.

ప్రశ్న 8.
అవొగాడ్రో నియమాన్ని తెలపండి.
జవాబు:
అవొగాడ్రో నియమం :
“స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద సమాన ఘనపరిమాణం గల వాయువులన్నింటిలో సమాన సంఖ్యలో అణువులుంటాయి.” గణితం ప్రకారం ఈ క్రింది విధంగా వ్రాస్తారు.
V ∝ n (P, T లు స్థిరం) లేక \(\frac{V}{n}\) = స్థిరం (P, Tలు స్థిరం)

ప్రశ్న 9.
స్థిర ఘనపరిమాణ రేఖలు (Isochores) అంటే ఏమిటి?
జవాబు:
ఒక వాయువులో ఉష్ణోగ్రతా, పీడనాల మధ్య మార్పును స్థిర ఘనపరిమాణం వద్ద గమనించుటకు గీయు గ్రాఫ్లను సమ ఘనపరిమాణ రేఖలు అంటారు (Isochores).

ప్రశ్న 10.
STP పరిస్థితులను తెలపండి.
జవాబు:
STP అనగా ప్రమాణ ఉష్ణోగ్రతా పీడనాలు
ప్రమాణ ఉష్ణోగ్రత = 273 K
ప్రమాణ పీడనం = 1 atm = 76 cm = 760 mm. Hg.
STP వద్ద ఒక మోల్ వాయువు 22.4 లీ. ఘనపరిమాణం ఆక్రమిస్తుంది.

ప్రశ్న 11.
గ్రామ్ మోలార్ ఘనపరిమాణం అంటే ఏమిటి?
జవాబు:
వాయుస్థితిలో ఒక గ్రామ్మోల్ వాయువు ఆక్రమించే ఘనపరిమాణాన్ని గ్రామ్ మోలార్ ఘనపరిమాణం అంటారు.

STP వద్ద ఒక మోల్ వాయువు 22.4 లీ. ఘనపరిమాణం ఆక్రమిస్తుంది.

ప్రశ్న 12.
ఆదర్శ వాయువు అంటే ఏమిటి?
జవాబు:
అన్ని ఉష్ణోగ్రతా పీడనాల వద్ద వాయు నియమాలన్నింటినీ (లేక) వాయు సమీకరణాన్ని తృప్తిపరిచే వాయువును ఆదర్శ వాయువు అంటారు.

ప్రశ్న 13.
వాయు స్థిరాంకం ‘R’ ను విశ్వవాయు స్థిరాంకం అని ఎందుకు పిలుస్తారు?
జవాబు:
R అనునది ఒక స్థిరాంకం. దీని విలువ అన్ని వాయువులకు ఒకే విధంగా ఉండుటచే దీనిని సార్వత్రిక వాయు స్థిరాంకం అంటారు.

ప్రశ్న 14.
ఆదర్శ వాయు సమీకరణాన్ని స్థితి సమీకరణం అని ఎందుకు అంటారు?
జవాబు:
ఆదర్శ వాయు సమీకరణాన్ని స్థితి సమీకరణం అని అంటారు. ఎందువలన అనగా ఈ సమీకరణం నాలుగు చరాంకాల మధ్య సంబంధం (P, V, n, T) మరియు ఇది ఏ వాయువు స్థితినైనా వివరిస్తుంది.

ప్రశ్న 15.
వాయు స్థిరాంకం ‘R’ విలువను వివిధ ప్రమాణాల్లో తెలపండి.
జవాబు:
R = 0.0821 lit. atm. k^-1 mol^-1
= 8.314 J. k1 mol^-1
= 1.987 cal. k^-1 mol^-1
= 8.314 × 10⁷ ergs. k^-1 mol^-1

ప్రశ్న 16.
ఒక వాయువు యొక్క సాంద్రత, మోలార్ ద్రవ్యరాశుల మధ్య సంబంధాన్ని తెలపండి.
జవాబు:

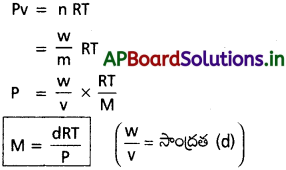
ప్రశ్న 17.
గ్రాహం వాయు వ్యాపన నియమాన్ని తెలపండి. [Mar, ’14]
జవాబు:
ఒక వాయువు వ్యాపన రేటు దాని సాంద్రత వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది.
r ∝ \(\frac{1}{\sqrt{d}}\)
r = వాయు వ్యాపన వేగం
d = వాయు సాంద్రత

ప్రశ్న 18.
N₂, O₂, CH₄, వాయువులలో ఏది త్వరితంగా వ్యాపనం చెందుతుంది. ఎందువల్ల? [T.S. Mar. ’15]
జవాబు:
N₂ అణుభారం = 28
O₂ అణుభారం = 32
CH₄ అణుభారం = 16
∴ తక్కువ అణుభారం గల వాయువు త్వరగా వ్యాపనం చెందుతుంది. కాబట్టి, ఈ పై ఇవ్వబడిన సమస్యలో CH₄ త్వరగా వ్యాపనం చెందుతుంది.

ప్రశ్న 19.
సల్ఫర్ డయాక్సైడ్ కంటే మిథేన్ ఎన్ని రెట్లు త్వరితంగా వ్యాపనం చెందుతుంది ?
జవాబు:
రెండు రెట్లు వేగంగా వ్యాపిస్తుంది.

ప్రశ్న 20.
డాల్టన్ పాక్షిక పీడనాల నియమాన్ని తెలపండి. [Mar. ’14]
జవాబు:
స్థిర ఉష్ణోగ్రతా ఘనపరిమాణాలలో ఒక వాయు మిశ్రమం కలిగించే పీడనం ఆ మిశ్రమంలోని అనుఘటక వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానం.
p = p₁ + p₂ + p₃
p వాయు మిశ్రమం పీడనం
p₁, p₂, p₃ = పాక్షిక పీడనాలు.

ప్రశ్న 21.
ఒక వాయువు పాక్షిక పీడనానికి, దాని మోల్ భాగానికి గల సంబంధాన్ని తెలపండి.
జవాబు:
పాక్షిక పీడనం = మొత్తం పీడనం × మోల్ భాగం.
P_A = P_T × X_A

ప్రశ్న 22.
నీటి ఆవిరి సంతృప్త బాష్పపీడనం అంటే ఏమిటి?
జవాబు:
నీటి ఆవిరి, ద్రవరూప నీటితో సమతాస్థితిలో ఉన్నపుడు ఉత్పత్తి అయ్యే పీడనాన్ని నీటి ఆవిరి సంతృప్త బాష్పపీడనం అంటారు.

ప్రశ్న 23.
వాయువుల అణుచలన సిద్ధాంతంలోని ఏ రెండు అంశాలు ఆదర్శ ప్రవర్తన నుంచి నిజవాయువుల విచలనాన్ని వివరించలేవు?
జవాబు:
వాయు అణుచలన సిద్ధాంతంలోని ఈ క్రింది అంశాలు ఆదర్శ ప్రవర్తన నుంచి నిజ వాయువుల విచలనాన్ని వివరించలేదు.

• వాయు అణువుల మధ్య ఎటువంటి ఆకర్షణ మరియు వికర్షణ బలాలు లేవు.
• వాయువు ఆక్రమించు ప్రదేశంతో పోల్చితే వాయు అణువుల ఘనపరిమాణం లెక్కలో తీసుకోదగినది కాదు.

ప్రశ్న 24.
చలద్వాయు సమీకరణాన్ని రాసి, దానిలోని పదాలను తెలపండి.
జవాబు:
చలద్వాయు సమీకరణం: PV = \(\frac{1}{2}\) mnu²
ఇచ్చట P = వాయు పీడనం ; V = వాయు ఘనపరిమాణం ; m = వాయు అణువు ద్రవ్యరాశి ; n = వాయు అణువుల సంఖ్య ; u = RMS వేగం.

ప్రశ్న 25.
వాయు అణువుల గతిజశక్తిని లెక్కకట్టుటకు సమీకరణాన్ని తెలపండి.
జవాబు:

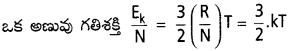
దీనిలో ‘k’ ను బోల్ట్స్మన్ స్థిరాంకం అంటారు. దీనినే ఒక అణువుకు వాయు స్థిరాంకం అంటారు.
దీని విలువ 1.38 × 10^-16 ఎర్గ్. డిగ్రీ^-1. అణువు^-1 (లేక) 1.38 × 10^-23 జౌల్. డిగ్రీ^-1. అణువు^-1
‘n’ మోల్ల వాయువులోని గతిశక్తి = n, E_k = \(\frac{3}{2}\) nRT

ప్రశ్న 26.
బోల్ట్మన్ స్థిరాంకం అంటే ఏమిటి? దాని విలువను తెలపండి.
జవాబు:
ఒక అణువుకు గల వాయు స్థిరాంకము విలువను బోల్ట్మన్ స్థిరాంకము అంటారు.
K = \(\frac{R}{N}\) దీని విలువ K = 1.38 × 10^-23 జౌల్స్. డిగ్రీ^-1. అణువు^-1.

ప్రశ్న 27.
RMS వేగం అంటే ఏమిటి?
జవాబు:
RMS వేగం (U_rms) :
వాయు అణువుల వేగాల వర్గాల సరాసరి యొక్క వర్గమూలాన్ని RMS వేగం అంటారు.

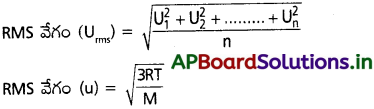
ప్రశ్న 28.
సగటు వేగం అంటే ఏమిటి?
జవాబు:
సగటు వేగం (U_av) :
ఒక వాయువులో అన్ని అణువుల వేగాల సగటు విలువ.

సగటు వేగం = 0.9213 × RMS వేగం.

ప్రశ్న 29.
గరిష్ఠ సంభావ్యత వేగం అంటే ఏమిటి?
జవాబు:
వాయువులోని అధిక సంఖ్య అణువులకు ఉండే వేగాన్ని గరిష్ఠ సంభావ్యతా వేగం అంటారు. (U_mp).
U = \(\sqrt{\frac{2RT}{M}}\)mp 2RT

ప్రశ్న 30.
వాయు అణువుల వేగాలపై ఉష్ణోగ్రత ప్రభావమేమిటి?
జవాబు:
వాయు అణుచలన సిద్ధాంతం ప్రకారం గతిజశక్తి, పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. ఉష్ణోగ్రతను పెంచితే వాయు అణువుల గతిశక్తి పెరిగి, వేగం పెరుగుతుంది.

ప్రశ్న 31.
వాయు అణువుల గతిజశక్తిపై ఉష్ణోగ్రత ప్రభావమేమిటి?
జవాబు:
వాయు అణుచలన సిద్ధాంతం ప్రకారం వాయు అణువుల గతిశక్తి పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉండును.
KE ∝ T_(పరమ)

ప్రశ్న 32.
వాయు అణువుల RMS వేగం, సగటు వేగం, గరిష్ఠ సంభావ్యత వేగాల నిష్పత్తిని తెలపండి.
జవాబు:

ప్రశ్న 33.
చలద్వాయు సమీకరణంలో RMS వేగాన్ని ఎందుకు తీసుకుంటారు?
జవాబు:
ఇచ్చిన వాయువులోని అణువులన్నింటి వేగాలు సమానంగా ఉండవు. వాయువు ఒక అణువు వేగం కూడా తాడనాల వలన నిరంతరం మారుతూ ఉంటుంది. కనుక అణువుల సగటు వేగాన్ని మాత్రమే లెక్కగట్టగలము.

ప్రశ్న 34.
సంపీడన గుణకం అంటే ఏమిటి?
జవాబు:
ఒకే ఉష్ణోగ్రత పీడనాలలో నిజవాయువు అసలైన మోలార్ ఘనపరిమాణం, ఆదర్శవాయు మోలార్ ఘనపరిమాణాల నిష్పత్తి
Z = \(\frac{PV}{nRT}\)
ఆదర్శ వాయువులకు 2 = 1.

ప్రశ్న 35.
బాయిల్ ఉష్ణోగ్రత అంటే ఏమిటి?
జవాబు:
కొంత పీడన పరిధిలో ఏ ఉష్ణోగ్రత వద్దనైతే నిజవాయువులు ఆదర్శ వాయు స్వభావాన్ని కలిగి ఉంటాయో ఆ బాయిల్ ఉష్ణోగ్రత అంటారు.

ప్రశ్న 36.
సందిగ్ధ ఉష్ణోగ్రత అంటే ఏమిటి? CO₂ కు దాని విలువ ఇవ్వండి.
జవాబు:
సందిగ్ధ ఉష్ణోగ్రత (T_c) :
“ఏ ఉష్ణోగ్రత కన్నా ఎక్కువ ఉష్ణోగ్రతల వద్ద పీడనాన్ని ఉపయోగించి వాయువును ద్రవీకరించలేమో ఆ ఉష్ణోగ్రతను వాయువు యొక్క సందిగ్ధ ఉష్ణోగ్రత అందురు.” దీనిని ‘T_c‘ తో సూచించెదరు. T_c విలువ వాయువు యొక్క అభిలాక్షణిక ధర్మం.

ప్రశ్న 37.
సందిగ్ధ ఘనపరిమాణం అంటే ఏమిటి?
జవాబు:
సందిగ్ధ ఘనపరిమాణం (V_c) : సందిగ్ధ పీడనం, సందిగ్ధ ఉష్ణోగ్రతల వద్ద ఒక గ్రామ్ మోల్ వాయువు ఆక్రమించు ఘనపరిమాణంను సందిగ్ధ ఘనపరిమాణం అందురు. దీనిని ‘V’ తో సూచించెదరు.

ప్రశ్న 38.
సందిగ్ధ పీడనం అంటే ఏమిటి?
జవాబు:
సందిగ్ధ పీడనం (P_c) :
సందిగ్ధ ఉష్ణోగ్రత వద్ద ఒక మోల్ వాయువును ద్రవీకరించుటకు అవసరమయిన పీడనంను సందిగ్ధ పీడనం అంటారు. దీనిని ‘P_c‘ తో సూచించెదరు.

ప్రశ్న 39.
సందిగ్ధ స్థిరాంకాలు అంటే ఏమిటి?
జవాబు:
సందిగ్ధ పీడనం, సందిగ్ధ ఉష్ణోగ్రత, సందిగ్ధ ఘనపరిమాణాలను సందిగ్ధ స్థిరాంకాలు అందురు.

ప్రశ్న 40.
ద్రవం బాష్ప పీడనాన్ని నిర్వచించండి.
జవాబు:
ద్రవం ఉపరితలంపై బాష్పం ఉత్పత్తి చేయు పీడనంను బాష్పపీడనం అంటారు. ద్రవం మరియు బాష్పం సమతాస్థితిలో ఉండవలెను.

ప్రశ్న 41.
సాధారణ, ప్రమాణ బాష్పీభవన ఉష్ణోగ్రతలు అంటే ఏమిటి? H₂O కు వాటి విలువలు ఇవ్వండి.
జవాబు:

• 1 అట్మాస్పియర్ పీడనం వద్ద బాష్పీభవన ఉష్ణోగ్రతలను సాధారణ బాష్పీభవన ఉష్ణోగ్రతలు అంటారు.
• 1 బార్ పీడనం వద్ద బాష్పీభవన ఉష్ణోగ్రతలను ప్రమాణ బాష్పీభవన ఉష్ణోగ్రతలు అంటారు.
• నీటి సాధారణ బాష్పీభవన ఉష్ణోగ్రత – 100° C.
• నీటి ప్రమాణ బాష్పీభవన ఉష్ణోగ్రత – 99.6° C.

ప్రశ్న 42.
కొండల మీద వంట చేయడానికి ప్రెజర్ కుక్కర్లను ఎందుకు వాడతారు?
జవాబు:
కొండ ప్రాంతంలో ఆహారం వండుటకు ప్రెషర్ కుక్కర్ ఉపయోగిస్తారు. ఎందువలన అనగా ఎత్తైన ప్రాంతాలలో తక్కువ వాతావరణ పీడనం ఉంటుంది. ఎత్తైన ప్రాంతాలలో ద్రవాలు తక్కువ ఉష్ణోగ్రతలలో బాష్పీభవనం చెందును. కావున నీరు కొండ ప్రాంతాలలో తక్కువ ఉష్ణోగ్రత వద్ద బాష్పీభవనం చెందును.

ప్రశ్న 43.
తలతన్యత అంటే ఏమిటి?
జవాబు:
తలతన్యత :
మెర్క్యురీని ద్రవం బొట్లు కొన్నింటిని ఒక తలంపై ఉంచినప్పుడు అది తలం మీద విస్తరణ చెందకుండా గోళాకార గుండుగా మారుతుంది. ఈ ప్రక్రియలు ద్రవాల ఒక అభిలాక్షణిక ధర్మంపై ఆధారపడి ఉంటాయి. ఈ ధర్మానే తలతన్యత అంటారు.

ప్రశ్న 44.
దళ ప్రవాహం (Laminar flow) అంటే ఏమిటి?
జవాబు:
ఒక ద్రవంలో ఒక్కొక్క పొరలోని అణువులు వేరు వేరు వేగాలలో ప్రయాణిస్తూ, ఒక క్రమపద్ధతిలో వేగాల్లో భేదాలున్న ఈ పొరల ప్రవాహాన్ని దళప్రవాహం (Laminar flow) అంటారు.

ప్రశ్న 45.
స్నిగ్ధతా గుణకం అంటే ఏమిటి? దాని ప్రమాణాలు తెలపండి.
జవాబు:
F = η A\(\frac{du}{dx}\) ; η (ఈటా) అనేది అనుపాత స్థిరాంకం. దీన్నే స్నిగ్ధతా గుణకం అంటారు.

స్నిగ్ధతా గుణకాన్ని వేగ ప్రవీణత స్పర్శా వైశాల్యాలు ఒక్కొక్కటి ఒక యూనిట్గా ఉన్నప్పుడు కావలసిన బలం అని నిర్వచించవచ్చు.
ప్రమాణాలు : g. cm^-1 sec^-1.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బాయిల్ నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
బాయిల్ నియమం :
‘స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది.” దీనిని గణితం ప్రకారం ఈ క్రింది విధంగా సూచిస్తారు.
V ∝ \(\frac{1}{P}\) (T స్థిరం) లేక V = k × \(\frac{1}{P}\) (T స్థిరం) లేక PV = K (T స్థిరం)
బాయిల్ నియమాన్ని ఈ క్రింది విధంగా కూడా నిర్వచించవచ్చు.

“స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం మరియు పీడనాల లబ్ధం ఎల్లప్పుడూ స్థిరంగా ఉంటుంది.”

ప్రశ్న 2.
ఛార్లెస్ నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
ఛార్లెస్ నియమం :
“స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది”. ఇదే ఛార్లెస్ నియమం.
V ∝ T
V = kT
\(\frac{V}{T}\) = k
ఇక్కడ V = ఘనపరిమాణం
T = పరమ ఉష్ణోగ్రత
k = స్థిరాంకం

స్థిర పీడనం వద్ద ఒక వాయువు ఘనపరిమాణాలు T₁ మరియు T₂ పరమ ఉష్ణోగ్రతల వద్ద V₁ మరియు V₂ లు అయిన
\(\frac{V_1}{T_1}=\frac{V_2}{T_2}\) = k

ప్రశ్న 3.
ఆదర్శ వాయు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
ఆదర్శవాయు సమీకరణాన్ని ఉత్పాదించుట :
వాయువు ఘనపరిమాణం, పీడనం, మోల్ల సంఖ్య మరియు పరమ ఉష్ణోగ్రతల మధ్యగల సంబంధాన్ని తెలియచేసే సమీకరణాన్ని ఆదర్శవాయు సమీకరణం అంటారు. బాయిల్, చార్లెస్, అవగాడ్రో నియమాలనుండి దీనిని ఈ క్రింది విధంగా ఉత్పాదిస్తారు.
బాయిల్ నియమం ప్రకారం, V ∝ \(\frac{1}{P}\) (T స్థిరం) ……………. (1)
చార్లెస్ నియమం ప్రకారం, V ∝ T (P స్థిరం) ……………. (2)
అవగాడ్రో నియమం ప్రకారం, V ∝ n (P, T లు స్థిరం) …………. (3)

పై మూడు సమీకరణాలను కలిపితే V ∝ \(\frac{1}{P}\) × T × n లేక V = R × \(\frac{1}{P}\) × T × n లేక PV = nRT
దీనినే ఆదర్శ వాయు సమీకరణం అంటారు.

ఇచ్చట P = వాయు పీడనం, V = వాయు ఘనపరిమాణం, T = వాయువు పరమ ఉష్ణోగ్రత, n = వాయువులోని మోల్ల సంఖ్య, Rను మోలార్ వాయు స్థిరాంకం అని, సార్వత్రిక వాయు స్థిరాంకం అని అంటారు.
n = 1 అయితే అంటే ఒక మోల్ వాయువును తీసుకుంటే పై ఆదర్శవాయు సమీకరణం, PV = RT గా మారుతుంది. లేక \(\frac{PV}{T}\) = R

ప్రశ్న 4.
గ్రాహం వాయు వ్యాపన నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
గ్రాహం వాయు వ్యాపన నియమము :
“స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద ఒక వాయువు వ్యాపన రేటు దాని సాంద్రత యొక్క వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది”. గణితాత్మకముగా, ఈ నియమాన్ని క్రింది విధంగా వ్రాస్తారు.
r ∝ \(\frac{1}{\sqrt{d}}\) (T, P లు స్థిరం) లేక r = K. \(\frac{1}{\sqrt{d}}\)
ఇచ్చట K ను వ్యాపనరేటు స్థిరాంకం ; n = వ్యాపన రేటు ; d వాయు సాంద్రత.

స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద రెండు వాయువుల వ్యాపన వేగాలు r₁, r₂ లు అని వాటి సాంద్రతలు d₁, d₂ లు అని అనుకుంటే, అపుడు గ్రాహం నియమం ప్రకారం

ప్రశ్న 5.
డాల్టన్ పాక్షిక పీడనాల నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
“స్థిర ఉష్ణోగ్రతా ఘనపరిమాణాలలో ఒక వాయు మిశ్రమం కలిగించే పీడనం ఆ మిశ్రమంలోని అనుఘటక వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానం”. ఇదే డాల్టన్ పాక్షిక పీడనాల నియమం.

ఒక వాయు మిశ్రమంలో మూడు వాయువులు ఒక పాత్రలో ఉన్నాయనుకుందాం. వాటి పాక్షిక పీడనాల P₁, P₂, P₃ అనుకుందాం. మిశ్రమం మొత్తం పీడనం ‘P’ అయితే డాల్టన్ పాక్షిక పీడనాల నియమం ప్రకారం.
P = P₁ + P₂ + P₃

ఆ మిశ్రమంలోని మూడు వాయువుల మోల్ సంఖ్యలు n₁, n₂, n₃ అనుకుందాం. “T” పరమ ఉష్ణోగ్రత వద్ద ఆ మిశ్రమం ఘనపరిమాణం “V” అయితే ఆదర్శవాయు సమీకరణం ప్రకారం

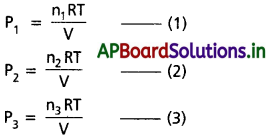
∴ మిశ్రమం మొత్తం పీడనం ‘P’ విలువ, P = P₁ + P₂ + P₃
డాల్టన్ నియమం ప్రకారం వాయు మిశ్రమం కలుగచేసే మొత్తం పీడనం

∴ సాధారణంగా, పాక్షిక పీడనం = మొత్తం పీడనం × మోల్ భాగం.

ప్రశ్న 6.
చలద్వాయు సమీకరణం నుండి (a) బాయిల్ నియమం (b) ఛార్లెస్ నియమం రాబట్టండి. [T.S. Mar. ’15]
జవాబు:
a) బాయిల్ నియమం :
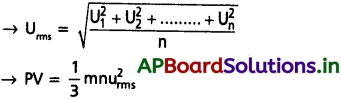
చలద్వాయు సమీకరణం : PV = \(\frac{1}{3}\) mnu²
ఇచ్చట P = వాయు పీడనం; V = వాయు ఘనపరిమాణం ; m = వాయు అణువు ద్రవ్యరాశి ; n = వాయు అణువుల సంఖ్య ; u = RMS వేగం.
వాయువు సగటు గతిశక్తి = \(\frac{1}{3}\) mnu²
అణుచలన సిద్ధాంతం ప్రకారం = \(\frac{1}{3}\) mnu² ∝ T (లేక) \(\frac{1}{3}\) mnu² = kT

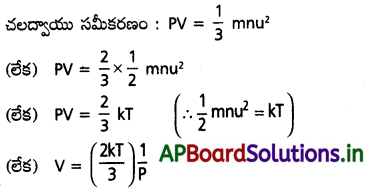
బాయిల్ నియమములో ఉష్ణోగ్రత స్థిరం, V = స్థిరం × \(\frac{1}{P}\) అవుతుంది.
(లేక) V ∝ \(\frac{1}{P}\) = (T స్థిరం)
ఇదే బాయిల్ నియమం.

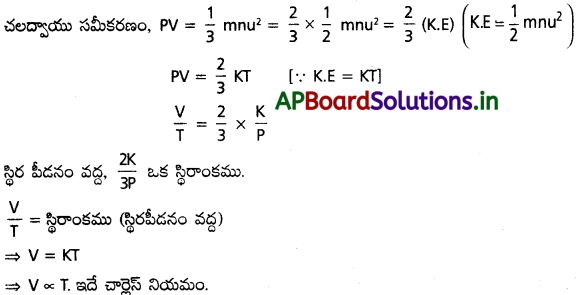
b) చార్లెస్ నియమం :

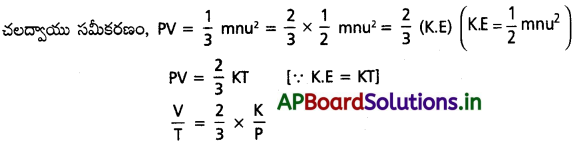
స్థిర పీడనం వద్ద, \(\frac{2K}{3P}\) ఒక స్థిరాంకము.
\(\frac{V}{T}\) = స్థిరాంకము (స్థిరపీడనం వద్ద)
⇒ V = KT
⇒ V ∝ T. ఇదే ఛార్లెస్ నియమం.

ప్రశ్న 7.
చలద్వాయు సమీకరణం నుండి (a) గ్రాహం నియమం (b) డాల్టన్ నియమం రాబట్టండి. [A.P. & T.S. Mar. ’15’]
జవాబు:
(a) గ్రాహమ్ వాయువ్యాపన నియమం :
చలద్వాయు సమీకరణం ప్రకారం PV = \(\frac{1}{3}\) mnu²
ఇందులో ‘mn’ వాయువు మొత్తం ద్రవ్యరాశిని సూచిస్తుంది.
‘n’ అవగాడ్రో సంఖ్య అయితే ‘m’ ఒక అణువు ద్రవ్యరాశి అనుకుంటే, అప్పుడు ‘mn’ విలువ గ్రాము అణుభారం (M) కు సమానమవుతుంది..
కాబట్టి PV = \(\frac{1}{3}\) Mu²

ఇదే గ్రాహమ్ వాయు వ్యాపన నియమం.

b) డాల్టన్ పాక్షిక పీడనాల నియమము :
‘V’ ఘనపరిమాణం గల ఒక పాత్రలో ఒక వాయువు ఒక్కొక్క అణువు ‘m₁‘ గ్రాముల భారం గల ‘n₁‘ అణువులను, u₁, RMS వేగం కలిగి ఉందనుకుందాం. ఆ వాయువు పీడనం ‘P₁‘ అయితే

ఈ వాయువును రెండో వాయువుతో తొలగించామనుకుందాం. రెండో వాయువు ఘనపరిమాణం V, పీడనం ‘P₂‘ అనుకుంటే రెండో వాయువుకు ‘n₂‘ అణువులు ఒక్కొక్క అణువు ‘m₂‘ గ్రాముల భారంతో “u₂” RMS వేగంతో ఉన్నాయనుకుంటే

ఇప్పుడు ఒకేసారి ఆ రెండు వాయువులను అదే పాత్రలో తీసికొంటే మిశ్రమం పీడనం ‘P’ అయితే

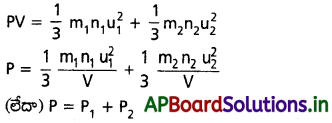
ఇదే డాల్టన్ పాక్షిక పీడనాల నియమం.

ప్రశ్న 8.
వాయు అణువుల గతిజశక్తికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
వాయువులో ఒక మోల్ అణువులు ఉన్నపుడు ‘n’ విలువ అవగాడ్రో సంఖ్య ‘N’ కు సమానమవుతుంది. అంటే ‘mN’ విలువ అణుభారం ‘M’ అవుతుంది.
చలద్వాయు సమీకరణం, PV = \(\frac{1}{3}\) mnu²

ఇచ్చట E_k అంటే 1 మోల్ వాయువు గతిశక్తి.
ఒక మోల్ వాయువుకు ఆదర్శ వాయు సమీకరణం : PV = RT
∴ \(\frac{2}{3}\) = E_k = RT (లేక) E_k = \(\frac{3}{2}\) RT
E_k విలువ ‘R’ ప్రమాణాల పైన ఆధారపడి, పరమ ఉష్ణోగ్రతకు (T) అనులోమానుపాతంలో ఉంటుంది. వాయువు స్వభావంతో సంబంధం లేదు.
E_k ∝ T
అంటే ఒకే ఉష్ణోగ్రత వద్ద ఉన్న ఒక మోల్ అన్ని వాయువుల్లోని గతిజశక్తులు సమానం.

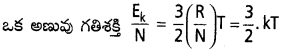
దీనిలో ‘k’ ను బోల్ట్స్మన్ స్థిరాంకం అంటారు. దీనినే ఒక అణువుకు వాయు స్థిరాంకం అంటారు.
దీని విలువ 1.38 × 10^-16 ఎర్గ్. డిగ్రీ^-1 అణువు^-1
(లేక) 1.38 × 10^-23 జౌల్. డిగ్రీ^-1, అణువు^-1
‘n’ మోల్ల వాయువులోని గతిశక్తి = n, E_k = \(\frac{3}{2}\) nRT

ప్రశ్న 9.
వాయు అణువుల (a) rms (b) సగటు వేగం (c) గరిష్ఠ సంభావ్యత వేగాలను నిర్వచించి, వాటి మధ్యగల సంబంధాన్ని తెలపండి.
జవాబు:
వాయువులోని అణువులకు మూడు రకాల వేగాలు వాడుకలో ఉన్నాయి. అవి గరిష్ఠ సంభావ్యతా వేగం, సగటు వేగం మరియు RMS వేగం.

గరిష్ట సంభావ్యతా వేగం (U_mp) :
గరిష్ఠ సంఖ్యలోని అణువులకు గల వేగాన్ని గరిష్ఠ సంభావ్యతా వేగం అంటారు.

RMS వేగం (u_rms) :
వాయు అణువుల వేగాల వర్గాల సరాసరి యొక్క వర్గమూలాన్ని RMS వేగం అంటారు.

సగటు వేగం (u_av) :
ఒక వాయువులో అన్ని అణువులు వేగాల సగటు విలువ.

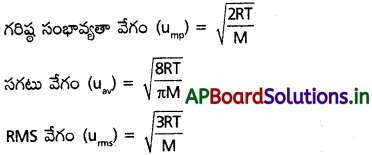
వీటిలో M = వాయువు అణుభారం, T = పరమ ఉష్ణోగ్రత, R వాయు స్థిరాంకం.
ఒక వాయువులో ‘n’ అణువులు ఉన్నాయని, వాటి వేగాలు వరుసగా u₁, u₂, …………. అనుకుంటే,

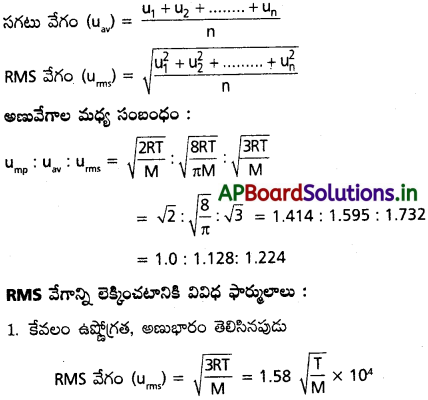
ప్రశ్న 10.
వాండర్ వాల్స్ స్థిరాంకాల భౌతిక ప్రాధాన్యతను వివరించండి.
జవాబు:
వాండర్ వాల్స్ సమీకరణం : (P + \(\frac{an^2}{V^2}\)) [V – nb] = nRT
P = వాయు పీడనము
n = వాయు మోల్ల సంఖ్య
a, b = వాండర్ వాల్ పారామీటర్లు
V = పాత్ర ఘనపరిమాణము
R = వాయు స్థిరాంకము
T = ప్రమాణ ఉష్ణోగ్రత
‘a’ ప్రమాణాలు – bar. lit^-2. mole^-2
‘b’ ప్రమాణాలు – lit. mol^-1

a, b ప్రాధాన్యత :-

• ‘a’ వాయువులోని అంతర అణుబలాలు కొలమానం. ఇది ఉష్ణోగ్రత పీడనాలపై ఆధారపడదు. ‘a’ విలువ ఎక్కువగా ఉన్నపుడు వాయువు త్వరగా ద్రవీకరింపబడును.
• ‘b’ వాయువు యొక్క ప్రభావిత ఘనపరిమాణంను సూచిస్తుంది. ఇది వాయు అణువుల ప్రభావిత పరిమాణంను సూచిస్తుంది. ‘b’ విలువ ఎక్కువ పరిధిలో పీడన, ఉష్ణోగ్రతల వద్ద స్థిరంగా ఉన్నపుడు వాయువును సంపీడనం చేయుట కష్టం.

ప్రశ్న 11.
ద్రవాల తలతన్యత అంటే ఏమిటి? ద్రవాల తలతన్యతపై ఉష్ణోగ్రత ప్రభావాన్ని వివరించండి.
జవాబు:
తలతన్యత :
మెర్క్యురీని ద్రవం బొట్లు కొన్నింటిని ఒక తలంపై ఉంచినప్పుడు అది తలం మీద విస్తరణ చెందకుండా, గోళాకార గుండుగా మారుతుంది. ఈ ప్రక్రియలు ద్రవాల ఒక అభిలాక్షిణిక ధర్మంపై ఆధారపడి ఉంటాయి. ఈ ధర్మానే తలతన్యత అంటారు.

ద్రవం లోపలి అణువు ఒకదాన్ని ఉదాహరణగా తీసుకుంటే దానిపై పనిచేసే అంతరణు బలాలు అన్ని దిశల్లోనూ ఉండి దానిపై పనిచేసే నికర బలం ఏమీ ఉండదు. అదే ఉపరితల అణువును చూస్తే దానిపై అంతరణు బలాలు కేవలం లోపలి వైపునే పనిచేస్తాయి. దీని వల్ల ఆ అణువుపై నికర ఆకర్షణ బలాలు అణువును ద్రవం లోపలికి లాగుతాయి. దీనివల్ల ద్రవం ఉపరితల వైశాల్యం సాధ్యమైనంతగా తగ్గడానికి ప్రయత్నిస్తుంది. తలతన్యతను γ(gamma) అనే గ్రీకు అక్షరంతో సూచిస్తారు.

తలతన్యత సంఖ్యాపరంగానూ, మితులపరంగానూ ఉపరితల శక్తికి సమానంగా ఉంటుంది. దీని మితులు kg.s^-2 లేదా SI ప్రమాణాల్లో Nm^-1.

20° C వద్ద తలతన్యత ద్రవం	dynes/cm తలతన్యత
డై ఇథైల్ ఈథర్	16.9
ఎసిటోన్	23.7
కార్బన్ టెట్రా క్లోరైడ్	26.9
ఇథనోల్	22.3
నీరు	72.8

ప్రశ్న 12.
ద్రవాల బాష్ప పీడనం అంటే ఏమిటి ? ద్రవాల బాష్ప పీడనం, వాటి బాష్పీ భవన ఉష్ణోగ్రతల మధ్య సంబంధాన్ని తెలపండి.
జవాబు:
ద్రవము మరియు ద్రవం యొక్క భాష్పము సమతాస్థితిలో ఉన్నపుడు భాష్పం ఉత్పత్తి చేయు పీడనాన్ని భాష్పపీడనం అంటారు.

• ఉష్ణోగ్రత పెరిగినపుడు వాయు అణువుల సగటు గతిశక్తి పెరిగి భాష్పపీడనం కూడా పెరుగును.
• ఏ ఉష్ణోగ్రత వద్దనైతే వాతావరణ పీడనం మరియు ద్రవం యొక్క భాష్పపీడనం సమానమవుతుందో ఆ ఉష్ణోగ్రతను భాష్పీ భవన స్థానం అంటారు.
• బాహ్య పీడనం పెంచినపుడు ద్రవం యొక్క భాష్పీభవన ఉష్ణోగ్రత పెరుగును.

ప్రశ్న 13.
స్నిగ్ధత, స్నిగ్ధతా గుణకాలను నిర్వచించండి. ద్రవాల స్నిగ్ధత ఉష్ణోగ్రతతో ఏవిధంగా మారుతుంది?
జవాబు:
స్నిగ్ధత :
స్నిగ్ధత అనేది ద్రవం ప్రవహించడానికి వీలుకాకుండా వ్యతిరేకించే బలాలను తెలియజెప్పేది (లేదా) కొలిచేది. ఘన ఉపరితలం మీద ఉండే ద్రవపు పొరలోని అణువులు దాదాపు కదలిక లేకుండా స్థిరంగా ఉంటాయి. తరువాతి పొరలోని అణువులు ఇంకొంత ఎక్కువ వేగంతో కదులుతాయి. ఈ విధంగా ఘన ఉపరితలం నుంచి ఒక ద్రవపు పొర ఎంత దూరంగా ఉంటే ఆ పొరలోని అణువులు అంత వేగంగా కదులుతున్నాయి. ఈ విధంగా ఒక్కొక్క పొరలోని అణువులు ఒక్కొక్క వేగంతో ప్రయాణిస్తూ ఒక క్రమ పద్ధతిలో వేగాల్లో భేదాలున్న ఈ పొరల ప్రవాహాన్ని లామినార్ ప్రవాహం అంటారు.

ఘన ఉపరితలం నుంచి మనం తీసుకున్న పొర dx దూరంలో ఉందనుకుందాం. దాని వేగంలో మార్పు ‘dv’ అనుకుందాం. అప్పుడు దాని వేగ ప్రవీణత \(\frac{dv}{dx}\) అవుతుంది. పొరల ప్రవాహాన్ని నడపడానికి ఒక బలం కావాలి. ఈ బలం పొరలు ఘన తలంపై స్పర్శిస్తున్న వైశాల్యం మీద, వేగ ప్రవణత మీద ఆధారపడి ఉంటాయి.

F = η A \(\frac{dv}{dx}\); n (ఈటా) అనేది అనుపాత స్థిరాంకం. దీన్నే స్నిగ్ధతా గుణకం అంటారు.

స్నిగ్ధతా గుణకాన్ని వేగ ప్రవీణత స్పర్శా వైశాల్యాలు ఒక్కొక్కటి ఒక యూనిట్గా ఉన్నప్పుడు కావలసిన బలం అని నిర్వచించవచ్చు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
అంతరఅణుబలాలను వివరించండి.
జవాబు:
అంతరఅణు బలాలు :
i) అయాన్-ద్విధ్రువ బలాలు :

నీటి అణువులు ధ్రువాణువులు. ఈ అణువుల్లో హైడ్రోజన్ పరమాణువులపై పాక్షిక ధనావేశం ఆక్సిజన్పై పాక్షిక ఋణావేశం ఉంటాయి. దీనికి కారణం హైడ్రోజన్, ఆక్సిజన్ల మధ్య ఉన్న ఋణ విద్యుదాత్మకత భేదమే. సోడియం క్లోరైడ్ లాంటి అయానిక సమ్మేళనాలను నీటిలో కరిగించినప్పుడు అవి Na⁺, Cl^– లాంటి ఘటక అయాన్లుగా విడిపోతాయి. అప్పుడు నీటి అణువులు ద్విధ్రువ అణువులు కాబట్టి వాటి ధనావేశం ఋణ అయాన్ వైపు, ఋణావేశం ధన అయాన్ వైపు దిగ్విన్యాసం చెందుతాయి. అంతర్ ఆకర్షణ శక్తి పరిమాణం అయాన్ మీది విద్యుదావేశం ‘Z’ మీద, ద్విధ్రువ బలం మీద, ద్విధ్రువం, అయానుల మధ్య దూరం వర్గానికి (r²) విలోమానుపాతంగాను ఉంటాయి. E = Zµ/ r² అయాన్-ద్విధ్రువ భ్రామక ఆకర్షణలు సోడియం క్లోరైడ్ వంటి అయానిక పదార్థాల జలద్రావణాల్లో ప్రధానమయినవి. అయాన్ల చుట్టూ ద్రావణి ద్విధ్రువ అణువులు చేరతాయి.

ii) ద్విధృవ-ద్విధృవ ఆకర్షణలు :

ద్విధ్రువ అణువులు తటస్థ అణువులైనప్పటికీ ద్విధృవ -ద్విధృవ ఆకర్షణలకు లోనవుతాయి. ఇవి పక్క పక్క ద్విధ్రువ అణువుల మధ్యగల విద్యుదాకర్షణల వల్ల ఇవి జరుగుతాయి. ఈ బలాలు కూడా విజాతీయ ధ్రువాల మధ్య ఆకర్షణ, సజాతీయ ధ్రువాల మధ్య వికర్షణ చూపిస్తాయి. ఇవి అణువులు దిగ్విన్యాసంపై కూడా ఆధారపడి ఉంటాయి. ఒక అధిక సంఖ్య అణువుల మధ్య అంతిమ ఆకర్షణ, వికర్షణ శక్తుల ఘటక అణువులు విడివిడిగా చూపించే అంతరీల తలంపై ఆధారపడి ఉంటాయి. ఇవి సాధారణంగా బలహీనమయిన బలాలు, అందుకే ఈ అణువులు అతి దగ్గరగా ఉన్నప్పుడు మాత్రమే ప్రాముఖ్యతను సంతరించుకుంటాయి.

iii) లండన్ విక్షేపణ బలాలు :

తాత్కాల ద్విధ్రువ భ్రామకం చుట్టుప్రక్కలనున్న పరమాణువుల్లో తాత్కాలిక ద్విధ్రువ భ్రామకాలను ప్రేరేపిస్తుంది. దీని ఫలితంగా బలహీనమైన ఆకర్షణ బలాలు వృద్ధి చెందుతాయి. వీటిని లండన్ బలాలు లేదా విక్షేపణ బలాలు అంటారు. ఇవి చాలా తక్కువ విలువల్లో ఉంటాయి. వీటి శక్తుల విలువలు 1 – 10k J mol^-1 ల మధ్య ఉంటాయి. ఈ విలువ ఒక అణువు ఎలక్ట్రాన్ మేఘం ఎంత తేలికగా ప్రక్కనున్న విద్యుత్ క్షేత్రంతో విరూపణ చెందుతుందనే దాని మీద ఆధారపడి ఉంటుంది. ఈ ధర్మాన్నే ధ్రువణశీలత అంటారు. అణువు లేదా పరమాణువు చిన్నదైతే దాని ధ్రువణశీలత తక్కువగా ఉండి తక్కువ విక్షేపణ బలాలతో ఉంటుంది. దీనికి కారణం ఒక పెద్ద అణువు లేదా పరమాణువుకు ఎక్కువ ధ్రువణశీలత ఉండి అధిక విక్షేపణ బలాలు ఉంటాయి. దీనికి కారణం వీటిల్లో ఆకర్షణ బలాలు ఉన్న ఎలక్ట్రాన్లు తక్కువగా ఉండటమే. దీనికి కారణం వీటిల్లో అధిక సంఖ్యలో ఎలక్ట్రాన్లు ఉండి అందులో కొన్ని కేంద్రకానికి దూరంగా ఉండి తక్కువ ఆకర్షణతో బంధించడమే.

iv) ద్విధృవ-ప్రేరిత ద్విధృవ బలాలు :
ఇవి శాశ్వత ద్విధ్రువభ్రామకం ఉన్న అణువులకు శాశ్వత ద్విధ్రువ భ్రామకం లేని అణువులకు మధ్య ఉత్పన్నమవుతాయి. శాశ్వత ద్విధ్రువ భ్రామకంతో ధ్రువాణువులు తటస్థ అణువుల ఎలక్ట్రాన్ మేఘాలను విరూపకత చెందిస్తాయి. ఆ తటస్థ అణువుల్లో ద్విధ్రువ లక్షణాన్ని ప్రేరేపిస్తాయి. ఇక్కడ కూడా అంతర్ ప్రభావిత శక్తి 1/2 కు అనులోమానుపాతంలో ఉంటుంది. ” అనేది అణువుల మధ్య దూరం. ఈ ప్రేరిత ద్విధ్రువ భ్రామకం విలువ తిరిగి శాశ్వత ద్విధృవ అణువు ద్విధ్రువ భ్రామకం విలువ మీద, తటస్థ అణువు ధ్రువణ శీలత మీద కూడా ఆధారపడి ఉంటుంది. పెద్ద అణువులు తేలికగా ధ్రువణం చెందుతాయి. ఇక్కడ కూడా విక్షేపణ బలాల సంచాయక ప్రభావం ద్విధ్రువ – ప్రేరిత ద్విధ్రువ ఆకర్షణలు ఉంటాయి.

ఎలక్ట్రాన్ – ఎలక్ట్రాన్ లేదా కేంద్రం – కేంద్రంల మధ్య వికర్షణ బలాల వల్ల పరమాణువులు, అణువులు లేదా అయాన్ల మధ్య వికర్షణలు ఉంటాయి.

ప్రశ్న 2.
బాయిల్, ఛార్లెస్, అవొగాడ్రో నియమాలను తెలిపి, ఆదర్శ వాయు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
వాయు ధర్మాలైన ఉష్ణోగ్రత (T), పీడనం (P), ఘనపరిమాణం (V), మోల్ల సంఖ్య (n) మధ్య గల సంబంధాలను తెలియచేసే వాటిని వాయు నియమాలు అంటారు. ఇవి ముఖ్యంగా మూడు ఉన్నాయి.

1. బాయిల్ నియమం
2. చార్లెస్ నియమం
3. అవగాడ్రో నియమం

1. బాయిల్ నియమం :
“స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది.” దీనిని గణితం ప్రకారం ఈ క్రింది విధంగా సూచిస్తారు.
V ∝ \(\frac{1}{P}\) (T స్థిరం) లేక V = k × \(\frac{1}{P}\) (T స్థిరం) లేక PV = K (T స్థిరం)

బాయిల్ నియమాన్ని ఈ క్రింది విధంగా కూడా నిర్వచించవచ్చు.

“స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం మరియు పీడనాల లబ్ధం ఎల్లప్పుడూ స్థిరంగా ఉంటుంది.”

2. ఛార్లెస్ నియమం :
“స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది”. ఇదే చార్లెస్ నియమం.
V ∝ T
V = kT
\(\frac{V}{T}\) = k
ఇక్కడ V = ఘనపరిమాణం
T= పరమ ఉష్ణోగ్రత
k = స్థిరాంకం

స్థిర పీడనం వద్ద ఒక వాయువు ఘనపరిమాణాలు T₁ మరియు T₂ పరమ ఉష్ణోగ్రతల వద్ద V₁ మరియు V₂ లు అయిన
\(\frac{V_1}{T_1}=\frac{V_2}{T_2}\) = k

3. అవగాడ్రో నియమం :
“స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద సమాన ఘనపరిమాణం గల వాయువులన్నింటిలో సమాన సంఖ్యలో అణువులుంటాయి.” గణితం ప్రకారం ఈ క్రింది విధంగా వ్రాస్తారు.
V ∝ n (P, T లు స్థిరం) లేక \(\frac{V}{n}\) = స్థిరం (P, Tలు స్థిరం)

ఆదర్శవాయు సమీకరణాన్ని ఉత్పాదించుట:
వాయువు ఘనపరిమాణం, పీడనం, మోల్ల సంఖ్య మరియు పరమ ఉష్ణోగ్రతల మధ్యగల సంబంధాన్ని తెలియచేసే సమీకరణాన్ని ఆదర్శవాయు సమీకరణం అంటారు. బాయిల్, చార్లెస్, అవగాడ్రో నియమాలనుండి దీనిని ఈ క్రింది విధంగా ఉత్పాదిస్తారు.
బాయిల్ నియమం ప్రకారం,
V ∝ \(\frac{1}{P}\) (T స్థిరం) …………… (1)
ఛార్లెస్ నియమం ప్రకారం, V∝ T (P స్థిరం) ……………. (2)
అవగాడ్రో నియమం ప్రకారం, V ∝ n (P, T లు స్థిరం) ……………. (3)
పై మూడు సమీకరణాలను కలిపితే V ∝ \(\frac{1}{P}\) × T × n (లేక) V = R × \(\frac{1}{P}\) × T × n లేక PV = nRT
దీనినే ఆదర్శ వాయు సమీకరణం అంటారు.

ఇచ్చట P వాయు పీడనం, V = వాయు ఘనపరిమాణం, T వాయువు పరమ ఉష్ణోగ్రత, n = వాయువులోని మోల్ల సంఖ్య, R ను మోలార్ వాయు స్థిరాంకం అని, సార్వత్రిక వాయు స్థిరాంకం అని అంటారు.

n = 1 అయితే అంటే ఒక మోల్ వాయువును తీసుకుంటే పై ఆదర్శవాయు సమీకరణం, PV = RT గా మారుతుంది. లేక
\(\frac{PV}{T}\) = R

ప్రశ్న 3.
వాయువుల వ్యాపనంపై వ్యాసం రాయండి.
జవాబు:
గ్రాహం వాయు వ్యాపన నియమము :
“స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద ఒక వాయువు వ్యాపన రేటు దాని సాంద్రత యొక్క వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది”. గణితాత్మకముగా, ఈ నియమాన్ని క్రింది విధంగా వ్రాస్తారు.

r ∝ \(\frac{1}{\sqrt{d}}\) (T, P లు స్థిరం) లేక r = K. \(\frac{1}{\sqrt{d}}\)

ఇచ్చట K ను వ్యాపనరేటు స్థిరాంకం ; n = వ్యాపన రేటు ; d వాయు సాంద్రత.

స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద రెండు వాయువుల వ్యాపన వేగాలు r₁, r₂ లు అని వాటి సాంద్రతలు d₁, d₂ లు అని అనుకుంటే, అపుడు గ్రాహం నియమం ప్రకారం

∴ వాయు సాంద్రత = బాష్ప సాంద్రత × H₂ సాంద్రత.
రెండు వాయువుల బాష్ప సాంద్రతలు వరుసగా VD₁, VD₂ లు అని అనుకుంటే,
d₁ = VD₁ × H₂ సాంద్రత, d₂ = VD₂ × H₂ సాంద్రత అవుతుంది.
d₁, d₂ విలువలను పై సమీకరణంలో ప్రతిక్షేపిస్తే.

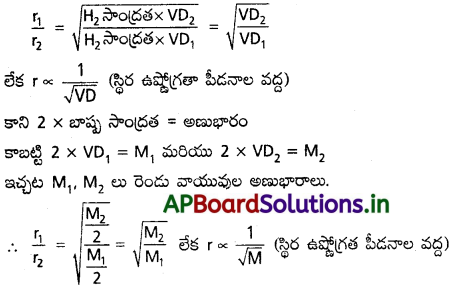
కాబట్టి, గ్రాహం నియమాన్ని ఈ క్రింది విధంగా కూడా వ్రాయవచ్చు.

స్థిర ఉష్ణోగ్రతా పీడన పరిస్థితుల వద్ద ఒక వాయువు యొక్క వ్యాపన రేటు దాని సాంద్రత, లేక బాష్ప సాంద్రత లేక అణుభారం యొక్క వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది.

ఒక వాయువు t₁ సెకన్ల కాలంలో V₁ మి.లీ., మరొక వాయువు t₂ సెకన్ల కాలంలో V₂ మి.లీ. వ్యాపనం చెందినవి అనుకుంటే, అపుడు వ్యాపనరేటు నిర్వచనం ప్రకారం,

2. రెండు వాయువుల వ్యాపన ఘనపరిమాణాలు సమానం అయితే (i.e., V = V, అయితే) అపుడు

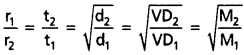
అనువర్తనాలు :

1. రెండు వాయువుల వ్యాపన వేగాలను పోల్చుట ద్వారా ఒకదాని అణుభారం తెలిస్తే రెండవదాని అణుభారం లెక్కగట్టవచ్చు.
2. ఒక మూలకం యొక్క సమస్థానీయాలను విడదీయవచ్చు.
3. మార్ష్ గ్యాస్ అలారం దీనిపై ఆధారపడి పనిచేస్తుంది.

ప్రశ్న 4.
డాల్టన్ పాక్షిక పీడనాల సిద్ధాంతాన్ని వివరించండి.
జవాబు:
“స్థిర ఉష్ణోగ్రతా ఘనపరిమాణాలలో ఒక వాయు మిశ్రమం కలిగించే పీడనం ఆ మిశ్రమంలోని అనుఘటక వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానం”. ఇదే డాల్టన్ పాక్షిక పీడనాల నియమం.
ఒక వాయు మిశ్రమంలో మూడు వాయువులు ఒక పాత్రలో ఉన్నాయనుకుందాం. వాటి పాక్షిక పీడనాలు P, P2, P3 అనుకుందాం. మిశ్రమం మొత్తం పీడనం ‘P’ అయితే డాల్టన్ పాక్షిక పీడనాల నియమం ప్రకారం.
P = P₁ + P₂ + P₃

ఆ మిశ్రమంలోని మూడు వాయువుల మోల్ల సంఖ్యలు n₁, n₂, n₃ అనుకుందాం. “గా పరమ ఉష్ణోగ్రత వద్ద ఆ మిశ్రమం ఘనపరిమాణం “V” అయితే ఆదర్శవాయు సమీకరణం ప్రకారం

∴ మిశ్రమం మొత్తం పీడనం ‘P’ విలువ, P = P₁ + P₂ + P₃
డాల్టన్ నియమం ప్రకారం, వాయుమిశ్రమం కలుగచేసే మొత్తం పీడనం

సాధారణంగా, పాక్షిక పీడనం = మొత్తం పీడనం × మోల్ భాగం.

ప్రశ్న 5.
వాయువుల అణుచలన సిద్ధాంతంలోని అంశాలను రాయండి.
జవాబు:
అణుచలన సిద్ధాంతంలోని ముఖ్యాంశాలు :

1. ప్రతి వాయువులోనూ సూక్ష్మాతి సూక్ష్మమైన అణువులు అనబడే కణాలు ఉంటాయి.
2. వాయు అణువులు నిరంతరం క్రమరాహిత్యంగా ఋజుమార్గంలో అత్యధిక వేగాలతో అన్ని దిశలలో ప్రయాణిస్తూ ఉంటాయి. అలా ప్రయాణించేటప్పుడు అవి తమలోతాము లేక పాత్రల యొక్క గోడలతో ఢీకొంటాయి. అందువలన వాటి దిశలో మార్పు వస్తుందేకాని శక్తి నష్టం మాత్రం జరగదు. అందువలననే వీటిని స్థితిస్థాపక తాడనాలు అంటారు.
3. వాయువు ఆక్రమించే ఘనపరిమాణంతో పోలిస్తే వాయు అణువులు ఆక్రమించే ఘనపరిమాణం చాలా తక్కువ.
4. వాయు అణువుల మధ్య ఏవిధమైన ఆకర్షణలు, వికర్షణలు ఉండవు.
5. వాయు అణువుల చలనాలపై భూమ్యాకర్షణ ప్రభావం ఉండదు.
6. వాయు అణువులు పాత్ర యొక్క గోడలపై తాడనాలు జరుపుట వలన వాయువులకు పీడనం ఏర్పడుతుంది. 7. వాయు అణువుల సగటు గతిశక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. E_k ∝ T.

ప్రశ్న 6.
చలద్వాయు సమీకరణం నుంచి వాయు నియమాలను రాబట్టండి.
జవాబు:
a) బాయిల్ నియమం :
చలద్వాయు సమీకరణం : PV = \(\frac{1}{2}\)mnu²
ఇచ్చట P = వాయు పీడనం ; V = వాయు ఘనపరిమాణం ; m = వాయు అణువు ద్రవ్యరాశి ; n = వాయు అణువుల సంఖ్య ; u = RMS వేగం.
వాయువు సగటు గతిశక్తి PV = \(\frac{1}{2}\)mnu²
అణుచలన సిద్ధాంతం ప్రకారం \(\frac{1}{2}\)mnu² ∝ T (లేక) \(\frac{1}{2}\)mnu² = kT
చలద్వాయు సమీకరణం : PV = \(\frac{1}{2}\)mnu²

బాయిల్ నియమములో ఉష్ణోగ్రత స్థిరం, V = స్థిరం × \(\frac{1}{P}\) అవుతుంది.
(లేక) V ∝ \(\frac{1}{P}\) (T స్థిరం)
ఇదే బాయిల్ నియమం.

b) గ్రాహమ్ వాయువ్యాపన నియమం :
1, 2 అనే రెండు వాయువులను తీసికొనుము. అపుడు రెండు వాయువులకు చలద్వాయు సమీకరణాలను ఈ క్రింది విధంగా వ్రాయవచ్చు.

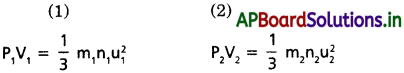
ఇచ్చట రెండు సమీకరణాలలోనూ P = పీడనం ; V = ఘనపరిమాణం ; m = అణువు ద్రవ్యరాశి ; n = అణువుల సంఖ్య ; u = RMS వేగం.
రెండు వాయువులు ఒకే పీడనం వద్ద ఉన్నాయని అనుకుంటే (i.e.,) P₁ = P₂.

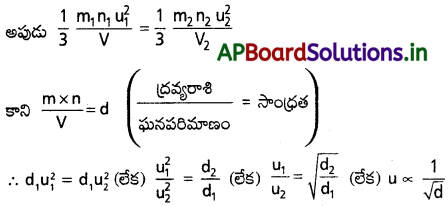
వాయు వ్యాపన వేగం (r) దాని RMS వేగానికి అనులోమానుపాతంలో ఉంటుంది. కాబట్టి r ∝ \(\frac{1}{\sqrt{d}}\) అవుతుంది. ఇదే గ్రాహం వాయు వ్యాపన నియమం.

c) చార్లెస్- నియమం :

ప్రశ్న 7.
మాక్స్వెల్ – బోల్ట్జ్మన్ అణువేగాల పంపిణీ వక్రరేఖలను వివరించండి. ఈ రేఖల ఆధారంగా తెలిసిన అంశాలేమిటి? అణువేగాల పంపిణీపై ఉష్ణోగ్రత ప్రభావాన్ని చర్చించండి.
జవాబు:

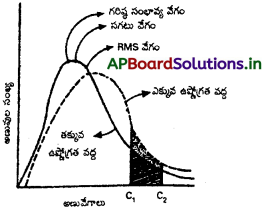
ఒక వాయువులోని అణువులన్నీ వివిధ వేగాలతో ప్రయాణిస్తూ ఉంటాయి. అవి తమలో తాము ఢీకొనడం వలన వాటి వేగాలు నిరంతరం మారుతూనే ఉంటాయి. అణువులు ‘0’ నుండి అత్యధిక విలువ వరకు ఉన్న అన్ని వేగాలతో చలిస్తూ ఉంటాయి.

అణువుల పరస్పర తాడనాల వల్ల వాటి వేగాలు ఎల్లప్పుడూ మారుతున్నప్పటికీ ఒక నిర్ణీత వేగం ఉన్న అణువుల సంఖ్యకు, మొత్తం అణువుల సంఖ్యకు గల నిష్పత్తి స్థిరంగా ఉంటుంది. ఈ నిష్పత్తిని సాంఖ్యక విధానాల ద్వారా గణిస్తారు. ఇలా లెక్కగట్టిన ఫలితాలు పటంలో చూపబడ్డాయి. ఈ పటాన్ని మాక్స్వెల్ – బోల్ట్మన్ అణువేగా వితరణ వక్రం అంటారు.

ఈ వక్రం క్రింది విషయాలు తెలియజేస్తుంది.

1. అతి తక్కువ వేగాలు, అత్యధిక వేగాలు ఉన్న అణువులు తక్కువగా ఉంటాయి.
2. వాయువులోని ఎక్కువ అణువుల వేగాలు ఒక గరిష్ఠ వేగానికి దగ్గరలో ఉంటాయి. వాయువులోని ఎక్కువ అణువులకు గల ఈ వేగాన్నే గరిష్ఠ సంభావ్యతా వేగం అంటారు.
3. అణువుల సగటు వేగం, గరిష్ఠ సంభావ్యతా వేగం కంటే ఎక్కువ. RMS వేగం సగటు వేగం కంటే ఎక్కువ.
4. వాయువులోని అధిక అణువుల వేగాలు, గరిష్ఠ సంభావ్యత లేదా సగటు వేగాల పరిధిలో ఉంటాయి.
5. ఉష్ణోగ్రత పెరిగితే వక్రం కుడివైపుకు జరిగి, ఎత్తు తగ్గి, వెడల్పు పెరుగుతుంది. అంటే అధిక ఉష్ణోగ్రత వద్ద తక్కువ వేగాలు ఉన్న అణువుల సంఖ్య తగ్గి, ఎక్కువ వేగాలు ఉన్న అణువుల సంఖ్య పెరుగుతుంది.

ప్రశ్న 8.
నిజ వాయువుల ప్రవర్తన, ఆదర్శ వాయు ప్రవర్తన నుంచి విచలనాన్ని వివరించండి.
జవాబు:
నిజవాయువుల ధర్మాలను తెలుసుకోవడానికి సంపీడన గుణకం చాలా అవసరం. దీన్ని ‘Z’ తో సూచిస్తారు. దీని విలువ ఒకే ఉష్ణోగ్రత, పీడనాల్లో నిజవాయువు అసలైన మోలార్ ఘనపరిమాణం, ఆదర్శవాయు మోలార్ ఘనపరిమాణాల నిష్పత్తి.

ఆదర్శ వాయువుకు ఏ పీడనం వద్దనైనా 2 = 1 ఉండాలి. ఇచ్చిన వాయువుల్లో O°C వద్ద హైడ్రోజన్ ఏ పీడనానికైనా ధన విచలనం చూపిస్తుంది. మిగిలిన వాయువులు ముందుగా ఋణ విచలనం చూపి పీడనాలు పెరిగిన తరువాత ధన విచలనం చూపిస్తున్నాయి. ఋణ విచలనాలు అంతరణు ఆకర్షణల వల్ల, ధన విచలనాలు అంతరణు వికర్షణల వల్ల వస్తాయి.

ఆదర్శ వాయువుకు Z = 1 కాబట్టి Z విలువ 7 నుంచి ఎంత మారుతుందనేది ఒక నిజవాయువు ఆదర్శ వాయు లక్షణం నుంచి ఎంత విచలనంతో ఉందో తెలియజేస్తుంది.

నిజ వాయువులకు Z విలువ పీడనంతో మారుతుంది. తక్కువ పీడనాల వద్ద కొన్ని వాయువులకు Z> 1 గా ఉంది. అంటే వాటి మోలార్ ఘనపరిమాణాలు ఆదర్శ వాయువుల కంటే తక్కువ. దీని అర్థం ఏమిటంటే ఇక్కడ అణువులు దగ్గర దగ్గరగా. గుచ్ఛాలుగా మారి ఆకర్షణ బలాలు ఎక్కువ కలిగి ఉంటాయని అధిక పీడనాల వద్ద దాదాపు అన్ని వాయువులకు Z విలువ ఒకటి కంటే ఎక్కువగా ఉంటుంది.

మధ్యస్థ పీడనాల్లో అధిక భాగం వాయువులకు Z < 1 ఉంటుంది. దీన్ని బట్టి నిజ వాయువులకు ఎక్కువ ఘనపరిమాణం ఉన్నప్పుడు ఆదర్శ వాయు ప్రవర్తన ఉంటుంది. కారణం అణువుల మధ్య దూరం ఎక్కువై అణువులు ఆక్రమించే వాస్తవ ఘనపరిమాణం పరిగణించదగినంత లేకపోవడమే.

ప్రశ్న 9.
వాండర్ వాల్స్ స్థితి సమీకరణాన్ని ఉత్పాదించండి. వాండర్ వాల్స్ సమీకరణం ప్రాముఖ్యతను వివరించండి.
జవాబు:
వాండర్ వాల్స్ స్థితి సమీకరణం :
J. వాండర్ వాల్స్ అంతర్ అణు అన్యోన్య చర్యలను పరిగణనలోకి తీసుకొని ఒక స్థితి సమీకరణాన్ని ఉత్పాదించాడు. ఇది నిజ వాయువులు, ఆదర్శ వాయు కోణాల నుంచి విచలనం చెందడానికి గల కారణాలను వివరిస్తుంది. దీన్ని క్రింది విధంగా వివరించవచ్చు.

రెండు అణువుల మధ్య వికర్షణ బలాలు ఆ రెండింటిని కొంత దూరాన్ని దాటి దగ్గరకు రానీయవు. అందువలన ఆ వాయు అణువులకు స్వేచ్ఛగా తిరిగేందుకు పాత్ర ఘనపరిమాణం మొత్తం (V) అందుబాటులో ఉండదు. దీనికి కారణం వాయువులోని ప్రతి అణువు కొంత ఘనపరిమాణం ఆక్రమించి ఇతర అణువులకు ఆ ఘనపరిమాణాన్ని స్వేచ్ఛగా తిరిగేందుకు లేకుండా చేస్తాయి. అందువల్ల ఆదర్శ వాయు సమీకరణంలో ఘనపరిమాణంలో సవరణ చేసి బదులు (V – nb) గా వ్రాయవచ్చు. ఇక్కడ ‘b’ అనుపాత స్థిరాంకం. ఇది పాత్ర తగ్గిన ఘనపరిమాణానికి అణువుల పరిమాణానికి సంబంధించిన స్థిరాంకం.
P = \(\frac{nRT}{V-nb}\)

పీడనం తక్కువైతే పాత్ర ఘనపరిమాణం అణువుల నిజ ఘనపరిమాణంతో పోల్చినప్పుడు చాలా ఎక్కువగా ఉంటుంది. అంటే (V > > nb) అందువల్ల ‘nb’ ని వదిలివేయవచ్చు. అప్పుడు సమీకరణం ఆదర్శ వాయు సమీకరణం అవుతుంది. అంటే వాయువు ఆదర్శ వాయువు లక్షణాలతో ఉంటుంది.

అంతర్ అణు ఆకర్షణ బలాల వల్ల అణువులు పాత్ర గోడలపై చేసే పీడనం ఆదర్శ వాయు అణువులు కలుగజేసే పీడనం కంటే తక్కువ. ఒక అణువుపై మిగతా అణువుల ఆకర్షణ బలాలు వాయువు గాఢత (n/V) కు అనులోమానుపాతంలో ఉంటాయి. ఆకర్షణ బలాల వల్ల అణువుల వేగం తగ్గుతుంది. అందువల్ల అవి పాత్ర గోడలపై ఢీకొనే పౌనఃపున్యం తగ్గుతుంది. అభిఘాతాలు కూడా బలహీనపడతాయి. అందువల్ల పీడనంలో తగ్గుదల వాయువు మోలార్ గాఢత వర్గానికి అనులోమానుపాతంలో ఉంటుంది. ఒక గాఢత విలువ అణువుల అభిఘాతాల పౌనఃపున్యం తగ్గుదల పరంగా, రెండో గాఢత విలువ అణువుల అభిఘాతం బలహీనపడటం.

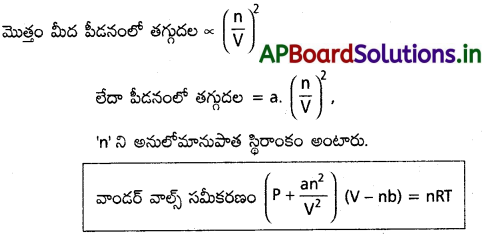
‘a’, ‘b’ లను వాండర్ వాల్స్ పారామీటర్లంటారు.

a, b ప్రాధాన్యత :

• ‘a’ వాయువులోని అంతర అణుబలాలు కొలమానం. ఇది ఉష్ణోగ్రత పీడనాలపై ఆధారపడదు. ‘a’ విలువ ఎక్కువగా ఉన్నపుడు వాయువు త్వరగా ద్రవీకరింపబడును.
• ‘b’ వాయువు యొక్క ప్రభావిత ఘనపరిమాణంను సూచిస్తుంది. ఇది వాయు అణువుల ప్రభావిత పరిమాణంను సూచిస్తుంది. ‘b’ విలువ ఎక్కువ పరిధిలో పీడన, ఉష్ణోగ్రతల వద్ద స్థిరంగా ఉన్నపుడు వాయువును సంపీడనం చేయుట కష్టం.

ప్రశ్న 10.
వాయువుల ద్రవీకరణలో ఇమిడి ఉన్న సూత్రాన్ని వివరించండి.
జవాబు:
ఏ వాయువైనా ద్రవీకరించబడాలంటే ముందు ఆ వాయువును దాని సందిగ్ధ ఉష్ణోగ్రత కంటే తక్కువ ఉష్ణోగ్రతకు చల్లబరచాలి. ఇచ్చిన పీడనం వద్ద ఒక వాయువును ద్రవీకరించాలంటే అది దాని ద్రవం బాష్పీభవన స్థానం కంటే తక్కువ ఉష్ణోగ్రతకు చల్లబరచాలి. ఉదాహరణకు, క్లోరిన్ ను గది పీడనం 1 అట్మాస్ఫియర్ వద్ద ద్రవీకరించాలంటే దాన్ని 34.0°C కు పొడి ఐస్బత్ లో చల్లబర్చాలి. నైట్రోజన్, ఆక్సిజన్లకు తక్కువ బాష్పీభవన స్థానాలు – 196°C, – 193°C ఉంటాయి. అందువల్ల వీటిని క్లోరిన్ ను ద్రవీకరించినంత తేలికగా ద్రవీకరించలేం. వీటిని ద్రవీకరించడానికి అంతర్ అణు బలాల సాంకేతిక పరిజ్ఞానాన్ని వాడతారు. ఇది క్రింది విధంగా ఉంటుంది. ముందు అణువుల వేగాల్ని తగినంత తగ్గిస్తే అణువుల మధ్య దూరాలు తగ్గి ఆకర్షణలు పెరుగుతాయి.

దానివల్ల చల్లబడ్డ వాయువులు ద్రవీకరణం చెందుతాయి. దీని కోసం అణువులను వీలున్న ఘనపరిమాణంలోకి వ్యాకోచింపచేస్తూ ఎలాంటి ఉష్ణశక్తి అందకుండా చూస్తారు. అప్పుడు అణువులు పక్క అణువుల అంతర్ అణు ఆకర్షణలను అధిగమించడానికి వాటి గతిజశక్తిలో కొంత భాగాన్ని స్థితిశక్తిగా మారుస్తాయి. అంటే అణువుల చలనవేగం తగ్గిపోతుంది. అందువల్ల అణువులు నెమ్మదిగా కదులుతాయి. వేగం తగ్గటం వల్ల వాయువు ఉష్ణోగ్రత తగ్గుతుంది. అంటే అది వ్యాకోచించక ముందు కంటే తక్కువగా చల్లబడుతుంది. దీని కోసం వాయువును ఒక సన్నని రంధ్రం ద్వారా వ్యాకోచింపజేస్తారు. ఈ విధంగా వాయువును అధిక పీడనం నుంచి తక్కువ పీడనం వైపుకు వ్యాకోంచిపజేసి చల్లబరచడాన్ని జౌల్ – థామ్సన్ ప్రభావం అంటారు. హైడ్రోజన్ ను సాధారణ పీడనాలు, ఉష్ణోగ్రతల వద్ద వ్యాకోచంలో వికర్షణ బలాలు ఎక్కువ కావడం వల్ల, Z > 1 అవుతుంది.

దీని వల్ల జౌల్ – థామ్సన్ వ్యాకోచంలో ఇది వేడక్కుతుంది. హైడ్రోజన్ లాంటి వాయువులను కూడా జౌల్ – థామ్సన్ వ్యాకోచంలో చల్లబరచాలంటే ముందు వాటిని ఒక కనీస ఉష్ణోగ్రతకు చల్లబరచాలి. దీన్ని ఆ వాయువు విలోమ ఉష్ణోగ్రత అంటారు. ఆ విధంగా చల్లబరచిన తరువాత దాన్ని వ్యాకోచింపజేయాలి. ఈ ప్రక్రియను అనేక సార్లు పునరావృతం చేస్తే అంటే చల్లబడిన వాయువును తిరిగి మిగిలిన వాయువుతో కలిపి ప్రసరింపచేస్తే చివరకు పాయు అణువులు చల్లబడి ద్రవంగా మారతాయి.

ప్రశ్న 11.
ద్రవాల క్రింది ధర్మాలను వివరించండి. (a) బాష్ప పీడనం (b) తలతన్యత (c) స్నిగ్ధత.
జవాబు:
a) ద్రవము మరియు ద్రవం యొక్క భాష్పము సమతాస్థితిలో ఉన్నపుడు భాష్పం ఉత్పత్తి చేయు పీడనాన్ని భాష్పపీడనం అంటారు.
ఉష్ణోగ్రత పెరిగినపుడు వాయు అణువుల సగటు గతిశక్తి పెరిగి భాష్పపీడనం కూడా పెరుగును.

• ఏ ఉష్ణోగ్రత వద్దనైతే వాతావరణ పీడనం మరియు ద్రవం యొక్క భాష్పపీడనం సమానమవుతుందో ఆ ఉష్ణోగ్రతను భాష్పీ భవన స్థానం అంటారు.
• బాహ్య పీడనం పెంచినపుడు ద్రవం యొక్క భాష్పీభవన ఉష్ణోగ్రత పెరుగును.

b) తలతన్యత :
మెర్క్యురీని ద్రవం బొట్లు. కొన్నింటిని ఒక తలంపై ఉంచినప్పుడు అది తలం మీద విస్తరణ చెందకుండా గోళాకార గుండుగా మారుతుంది. ఈ ప్రక్రియలు ద్రవాల ఒక అభిలాక్షణిక ధర్మంపై ఆధారపడి ఉంటాయి. ఈ ధర్మానే తలతన్యత అంటారు. ద్రవం లోపలి అణువు ఒకదాన్ని ఉదాహరణగా తీసుకుంటే దానిపై పనిచేసే అంతరణు బలాలు అన్ని దిశల్లోనూ ఉండి దానిపై పనిచేసే నికర బలం ఏమీ ఉండదు. అదే ఉపరితల అణువును చూస్తే దానిపై అంతరణు బలాలు కేవలం లోపలి వైపునే పనిచేస్తాయి. దీని వల్ల ఆ అణువుపై నికర ఆకర్షణ బలాలు అణువును ద్రవం లోపలికి లాగుతాయి. దీనివల్ల ద్రవం ఉపరితల వైశాల్యం సాధ్యమైనంతగా తగ్గడానికి ప్రయత్నిస్తుంది.

తలతన్యతను γ(gamma) అనే గ్రీకు అక్షరంతో సూచిస్తారు.
తలతన్యత సంఖ్యాపరంగానూ, మితులపరంగానూ ఉపరితల శక్తికి సమానంగా ఉంటుంది. దీని మితులు kg.s^-2 లేదా SI ప్రమాణాల్లో Nm^-1.

20° C వద్ద తలతన్యత ద్రవం	dynes/cm తలతన్యత
డై ఇథైల్ ఈథర్	16.9
ఎసిటోన్	23.7
కార్బన్ టెట్రా క్లోరైడ్	26.9
ఇథనోల్	22.3
నీరు	72.8

c) స్నిగ్ధత :
స్నిగ్ధత అనేది ద్రవం ప్రవహించడానికి వీలుకాకుండా వ్యతిరేకించే బలాలను తెలియజెప్పేది (లేదా) కొలిచేది. ఘన ఉపరితలం మీద ఉండే ద్రవపు పొరలోని అణువులు దాదాపు కదలిక లేకుండా స్థిరంగా ఉంటాయి. తరువాతి పొరలోని అణువులు ఇంకొంత ఎక్కువ వేగంతో కదులుతాయి. ఈ విధంగా ఘన ఉపరితలం నుంచి ఒక ద్రవపు పొర ఎంత దూరంగా ఉంటే ఆ పొరలోని అణువులు అంత వేగంగా కదులుతున్నాయి. ఈ విధంగా ఒక్కొక్క పొరలోని అణువులు ఒక్కొక్క వేగంతో ప్రయాణిస్తూ ఒక క్రమ పద్ధతిలో వేగాల్లో భేదాలున్న ఈ పొరల ప్రవాహాన్ని లామినార్ ప్రవాహం అంటారు.

ఘన ఉపరితలం నుంచి మనం తీసుకున్న పొర dx దూరంలో ఉందనుకుందాం. దాని వేగంలో మార్పు ‘dv’ అనుకుందాం. అప్పుడు దాని వేగ ప్రవీణత \(\frac{dv}{dx}\) అవుతుంది. పొరల ప్రవాహాన్ని నడపడానికి ఒక బలం కావాలి. ఈ బలం పొరలు ఘన తలంపై స్పర్శిస్తున్న వైశాల్యం మీద, వేగ ప్రవణత మీద ఆధారపడి ఉంటాయి.

F = ηA. \(\frac{dv}{dx}\); η (ఈటా) అనేది అనుపాత స్థిరాంకం. దీన్నే స్నిగ్ధతా గుణకం అంటారు.

స్నిగ్ధతా గుణకాన్ని వేగ ప్రవీణత స్పర్శా వైశాల్యాలు ఒక్కొక్కటి ఒక యూనిట్గా ఉన్నప్పుడు కావలసిన బలం అని నిర్వచించవచ్చు.

లెక్కలు (Problems)

ప్రశ్న 1.
30° C వద్ద 500 dm ఘనపరిమాణం 1 bar పీడనం గల గాలిని 200 dm3 ఘనపరిమాణానికి సంపీడనం చెందించడానికి కావలసిన కనిష్ట పీడనం ఎంత?
సాధన:
సూత్రము :
P₁V₁ = P₂V₂
P₁ = 1 bar
V₁ = 500 dm³
V₂ = 200 dm³
P₂ = ?
1 × 500 = P₂ × 200
ρ₂ = \(\frac{5}{2}\) = 2.5 bar.

ప్రశ్న 2.
35 °C 1.2 bar పీడనం వద్ద 120 mL ఘన పరిమాణం గల పాత్రలో కొంత పరిమాణం గల వాయువున్నది. ఈ వాయువును 180 mL ఘనపరిమాణం గల పాత్రలోనికి మార్చినపుడు దాని పీడనం ఎంత ఉంటుంది.
సాధన:
సూత్రము
P₁V₁ = P₂V₂
P₁ = 1.2 bar
V₁ = 120 మి.లీ.
V₂ = 180 మి.లీ.
P₂ = ?
1.2 × 120 = P₂ × 180
P₂ = \(\frac{2.4}{3}\) = 0.8 bar

ప్రశ్న 3.
pV = nRT స్థితి సమీకరణాన్ని ఉపయోగించి, ఇచ్చిన ఉష్ణోగ్రత వద్ద ఒక వాయువు సాంద్రత దాని పీడనానికి అనులోమానుపాతంలో ఉంటుందని చూపండి.
సాధన:
స్థితి సమీకరణం PV = nRT

పై సమీకరణం నుండి P ∝ d

ప్రశ్న 4.
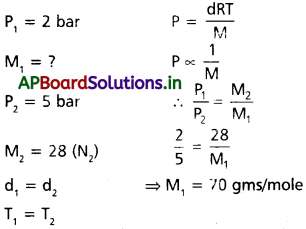
0°C వద్ద 2 bar పీడనం వద్ద ఒక వాయువు ఆక్సైడ్ సాంద్రత, 5 bar పీడనం వద్ద డైనైట్రోజన్ సాంద్రతకు సమానమవుతుంది. ఆక్సైడ్ మోలార్ ద్రవ్యరాశి ఎంత?
సాధన.
రెండు వాయువులు ఇవ్వబడ్డాయి, మొదటిది డైనైట్రోజన్ రెండవది తెలియనిది.
→ రెండు వాయువుల సాంద్రత సమానము.

సూత్రము :
ఇవ్వబడినవి

ప్రశ్న 5.
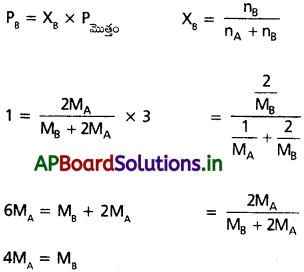
27 °C వద్ద 1 గ్రామ్ ఆదర్శ వాయువు A 2 bar పీడనం కలిగి ఉన్నది. అదే ఉష్ణోగ్రత వద్ద అదే పాత్రలోనికి 2g మరొక ఆదర్శవాయువు B ను పంపినపుడు పీడనం 3 barకు పెరిగింది. A, B వాయువుల మోలార్ ద్రవ్యరాశుల మధ్య సంబంధాన్ని కనుక్కోండి.
సాధన:
ఇవ్వబడినవి
‘A’ వాయువు భారము = 1 గ్రా.
‘B’ వాయువు భారము = 2గ్రా.
‘A’ వాయువు అణుభారము = M_A
‘B’ వాయువు అణుభారము = M_B
‘A’ వాయువు పీడనం = P_A = 2 bar
మొత్తము పీడనం P_A + P_B = 3 bar
∴ P_B = 3 – 2 = 2 bar

ప్రశ్న 6.
డ్రైనేజ్లను శుభ్రపరిచే డ్రైనెక్స్ కొద్ది పాళ్ళలో అల్యూమినియం కలిగి ఉండి కాస్టిక్ సోడాతో చర్యనొంది డైహైడ్రోజన్ను ఇస్తుంది. 20°C 1 bar పీడనం వద్ద 0.15g అల్యూమినియం చర్యనొందిన, ఎంత ఘనపరిమాణం గల డైహైడ్రోజన్ విడుదలవుతుంది?
సాధన:
రసాయన సమీకరణం
2Al + 2 NaOH + 2H₂O → 2NaAlO₂ + 3H₂
పై సమీకరణం నుండి
2 గ్రా. పరమాణువుల ‘Al’ 3 మోల్ల H₂ వాయువును
STP వద్ద విడుదల చేయును.
2 × 27 గ్రా. Al → 2 × 22.4 లీ H₂
0.15 గ్రా. Al → ?

ప్రశ్న 7.
27 °C వద్ద 9 dm’ పాత్రలో 3.2 g మిథేన్, 4.4 g కార్బన్ డైఆక్సైడ్ కలిగి ఉన్న వాయు మిశ్రమం కలిగించే పీడనం ఎంత?
సాధన:
3.2 గ్రా. CH₄ ఇవ్వబడినది

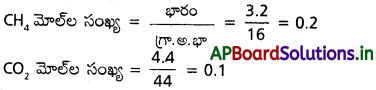
∴ n = n_CH4 + n_CO2
= 0.2 +0.1 = 0.3
R = 8.314
T = 27°C = 300 K
V = 9 dm³
సూత్రము :

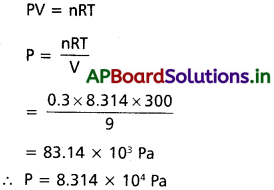
ప్రశ్న 8.
27°C వద్ద 1L పాత్రలోనికి 0.8 బార్ పీడనం కలిగిన 0.5 L డైహైడ్రోజన్, 0.7 బార్ కలిగిన 2.0 L డైఆక్సిజన్ పంపినపుడు ఆ వాయు మిశ్రమం కలిగించే పీడనం ఎంత ?
సాధన:
Case – I హైడ్రోజన్ వాయువు
P₁ = 0.8 bar
P₂ = ?
V₁ = 0.5 లీ,
V₂ = 1 లీ.
P₁V₁ = P₂V₂
P₂ = \(\frac{0.8\times0.5}{1}\)
= 0.4 bar
H₂ యొక్క పాక్షిక పీడనం = 0.4 bar
Case – II : ఆక్సిజన్ వాయువు
P₁ = 0.7 bar ; P₂ = ?
V₁ = 2 lit
V₂ = 1 lit
P₁V₁ = P₂V₂
P₂ = \(\frac{0.7\times2}{1}\) = 1.4 bar.
O₂ యొక్క పాక్షిక పీడనం = 1.4 bar.
మొత్తం పీడనం = P_H2 + P_O2
= 0.4 + 1.4 = 1.8 bar

ప్రశ్న 9.
27 °C, 2 బార్ పీడనం వద్ద ఒక వాయువు సాంద్రత 5.46 g/dm³ ఉంటే, STP వద్ద దాని సాంద్రత ఎంత?
సాధన:
ఇవ్వబడినవి
d₁ = 5.46 గ్రా/dm³
T₁ = 27° C = 300 K
P₁ = 2 bar
P₂ = 1.013 bar (STP)
T₂ = 273 K (STP) d₂ = ?

ప్రశ్న 10.
546 °C, 0.1 బార్ పీడనం వద్ద 34.05 mL ఫాస్ఫరస్ బాష్పం భారం 0.0625 g ఉంటే, ఫాస్ఫరస్ మోలార్ ద్రవ్యరాశి ఎంత?
సాధన:
P = 0.1 bar
w = 0.0625 గ్రా
R = 0.083 bar dm³/ k.mole
V = 340.5 × 10^-3 లీ.
T = 546° C = 819 K
సూత్రము :
PV = nRT

ప్రశ్న 11.
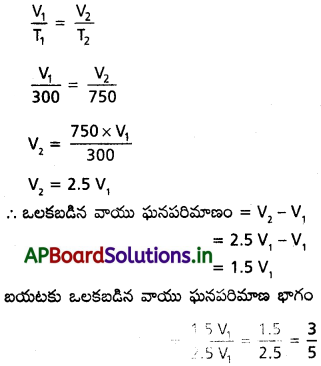
27 °C వద్ద ప్రయోగం చేసేటప్పుడు ఒక విద్యార్థి పాత్రలో చర్యా మిశ్రమాన్ని తీసుకోవడం మర్చి పోయి, పాత్రను వేడి చేస్తున్నాడు. కొంత సమయానికి తప్పు తెలుసుకొని, పాత్ర ఉష్ణోగ్రతను పైరో మీటర్ ద్వారా చూస్తే, ఉష్ణోగ్రత 477 °C ఉన్నది. ఎంత భాగం గాలి బయటకు పోయిందో లెక్క కట్టండి.
సాధన:
T₁ = 27° C = 300 K
T₂ = 477° C = 750 K
సూత్రము :

ప్రశ్న 12.
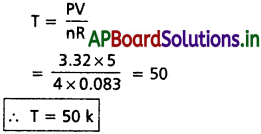
3.32 బార్ పీడనం వద్ద 4.0 మోల్ల వాయువు 5 dm³ ఘనపరిమాణం ఆక్రమించిన, ఆ వాయువు ఉష్ణోగ్రతను లెక్కకట్టండి.
(R = 0.083 bar dm³ K^-1 mol^-1)
సాధన:
P = 3.32 bar
V = 5 dm³
R = 0.083 bar dm³/ k.mole
n = 4 మోల్లు
సూత్రము :
PV = nRT

ప్రశ్న 13.
1.4 g డైనైట్రోజన్ వాయువులో ఉన్న మొత్తం ఎలక్ట్రాన్ల సంఖ్యను లెక్కకట్టండి.
సాధన:
14గ్రా. N₂ వాయువులో 6.023 × 10²³ పరమాణువులు కలవు
1.4 గ్రా. N₂ వాయువులో 6.023 × 10²² పరమాణువులు కలవు
ప్రతి ‘N’ పరమాణువులో 7 ఎలక్ట్రాన్లు కలవు. 1.4 గ్రా. నైట్రోజన్లో ఉండు ఎలక్ట్రాన్లు
= 6.023 × 10²² x 7
= 4.2161 × 10²³ ఎలక్ట్రాన్లు.

ప్రశ్న 14.
ప్రతి సెకనుకు 10¹⁰ ధాన్యపు గింజలను పంచు కుంటూ పోతే అవొగాడ్రో సంఖ్య ధాన్యపు గింజలను పంచటానికి ఎంత కాలం పడుతుంది?
సాధన:
ప్రతి సెకను కాలంలో 10¹⁰ ధాన్యపు గింజలను పంచ బడును అవగాడ్రో సంఖ్య అనగా 6.023 × 10²³
∴ 6.023 × 10²³ ధాన్యపు గింజలను పంచుటకు పట్టు సమయము.

ప్రశ్న 15.
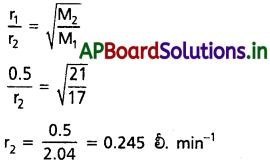
ఒక సన్నని రంధ్రం గుండా అమ్మోనియా వాయువు వ్యాపనం రేటు 0.5 lit min^-1 అదే పరిస్థితులలో క్లోరిన్ వాయువు వ్యాపనం రేటు కనుక్కోండి.
సాధన:
NH₃ వ్యాపనరేటు r₁ = 0.5 లీ. min^-1
NH₃ అణుభారం M₁ = 17
Cl₂ వ్యాపన రేట r₂ = ?
Cl అణుభారం M₂ = 71

సూత్రము :
గ్రాహం నియమం ఆధారంగా

ప్రశ్న 16.
CO₂, Cl₂ వాయువులు సాపేక్ష వ్యాపనం రేట్లు కనుక్కోండి.
సాధన:
సూత్రం :

ప్రశ్న 17.
150 ml కార్బన్ మోనాక్సైడ్ నిస్సరణం చెందడానికి 25 సెకనుల కాలం పట్టిన, అదే కాలంలో ఎంత ఘనపరిమాణం గల మిథేన్ వాయువు నిస్సరణం చెందుతుంది?
సాధన:

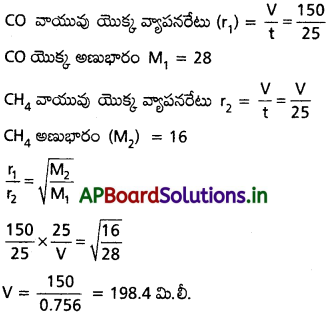
ప్రశ్న 18.
ఒక 100 మీటర్ల గొట్టంలోకి ‘A’ వైపు నుంచి హైడ్రోజన్ క్లోరైడ్ వాయువును ‘B’ వైపు నుంచి అమ్మోనియా వాయువును ఒకే పరిస్థితులలో పంపినట్లయితే, ‘A’ నుంచి ఎంత దూరంలో రెండు వాయువు కలుసుకొంటాయి?
సాధన:

• HCl మరియు NH₃ రెండు వాయువులు ఒక గొట్టంలోని రెండు చివరలు A మరియు B నుండి వ్యాపనం చెందుతున్నాయి.
• ఈ రెండు వాయువులు ‘O’ అను బిందువు వద్ద కలుసుకొనబడ్డాయి. దీనికి సూచనగా NH₄Cl ఒక తెల్లటి వలయంగా ఏర్పడునది.
• పటము నుండి AO దూరం = × మీ
• పటము నుండి OB దూరం = (100 – x) మీ.
  గ్రాహం వాయు వ్యాపన నియమం ప్రకారం
  HC మరియు NH₃ వ్యాపన రేట్లు

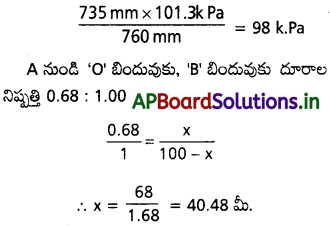
కావున ఈ రెండు వాయువులు A నుండి 40.48 మీ. దూరంలో కలుసుకొనబడ్డాయి.

ప్రశ్న 19.
27 °C వద్ద 1 dm³ పాత్రలో ఉన్న 8 g డైఆక్సిజన్, 4gడైహైడ్రోజన్ వాయువుల మిశ్రమం కలిగించే పీడనాన్ని లెక్కకట్టండి. (R = 0.083 bar dm³ K^-1 mol^-1.)
సాధన:
P = ?
V = 1 dm³
R = 0.083 bar dm³ /k.mole

ప్రశ్న 20.
27°C వద్ద 5dm’ పాత్రలో ఉన్న 3.5g డైనైట్రోజన్, 3.0g డైహైడ్రోజన్, 8.0g డై ఆక్సిజన్ వాయు వుల మిశ్రమం కలిగించే మొత్తం పీడనాన్ని కనుక్కోండి.
(R = 0. 083 bar dm³ k^-1 mol^-1)
సాధన:
V = 5 dm³
R = 0.083 bar dm³ (k.mole
T = 27°C = 300 K

ప్రశ్న 21.
స్థానభ్రంశం చెందిన గాలి ద్రవ్యరాశి, బెలూన్ ద్రవ్యరాశుల మధ్య భేదాన్ని పేలోడ్గా వ్యవహరిస్తారు. 27°C, 11.6 బార్ పీడనం వద్ద 10 మీ వ్యాసార్థం, 100 kg ద్రవ్యరాశి గల ఒక బెలూన్ను హీలియం వాయువుతో నింపినప్పుడు, బెలూన్ పేలోడ్ను లెక్కకట్టండి. (గాలి సాంద్రత 1.2 kg m3, R = 0.083 bar dm³ K^-1 mol^-1).
సాధన:
r = 10 మీ
m = 100 kg
T = 27° C = 300K
d = 1.22 kg/m³
బెలూన్ ఘనపరిమాణం = \(\frac{4}{3}\) πr³
=\(\frac{4}{3}\times\frac{22}{7}\) × 10³
= 4190.5 m³
P = 1.66 bar
T = 300 K
V = 4190.5 m³
R = 0.083 bar dm³ /k.mole
PV = nRT
సూత్రం :

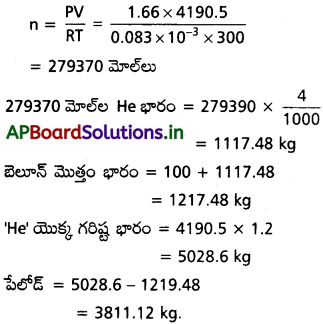
ప్రశ్న 22.
31.1°C, 1 bar పీడనం వద్ద 8.8 g CO వాయువు ఆక్రమించే మనపరిమాణాన్ని లెక్కకట్టండి.
R = 0.083 bar L K^-1 mol^-1.
సాధన:
PV = nRT
P = 1 bar
T = 31.1°C = 304.1 K
R = 0.083 bar dm³ × k^-1 mol^-1
n = \(\frac{8.8}{44}\) = 0.2
PV = nRT
1 × V = 0.2 × 0.083 × 304.1
= 5.04806 లీ.

ప్రశ్న 23.
95 °C వద్ద 2.9g ద్రవ్యరాశి గల ఒక వాయువు ఆక్రమించే ఘనపరిమాణం, అదే పీడనం వద్ద 17 °C వద్ద 0.184 g డైహైడ్రోజన్ ఆక్రమించే ఘనపరిమాణానికి సమానము. అయితే వాయువు మోలార్ ద్రవ్యరాశి ఎంత?
సాధన:
డై హైడ్రోజన్ మరియు తెలియని వాయువు ఇవ్వబడ్డాయి. తెలియని వాయువు
V₁ = V

ప్రశ్న 24.
1 బార్ పీడనం వద్ద డైహైడ్రోజన్, డై ఆక్సిజన్ వాయువుల మిశ్రమంలో డైహైడ్రోజన్ భార శాతము 20% అయినా, డైహైడ్రోజన్ పాక్షిక పీడనాన్ని లెక్కకట్టండి.
సాధన:
మిశ్రమం నందు 20% H, భారాత్మకంగా కలదు. కావున
80% ఆక్సిజన్ మిగిలియుండును.

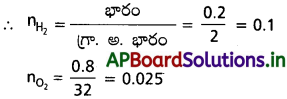
డైహైడ్రోజన్ పాక్షిక పీడనం = H₂మోల్ భాగం మొత్తం పీడనం
= 0.8 × 1 = 0.8 bar

ప్రశ్న 25.
pV²T²/n విలువకు SI ప్రమాణమేమిటి ?
సాధన:

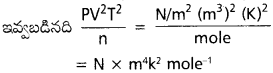
ప్రశ్న 26.
ఛార్లెస్ నియమం ప్రకారం – 273°C ను అత్యల్ప ఉష్ణోగ్రతగా ఎందుకు భావిస్తారో వివరించండి.
సాధన:
ఛార్లెస్ నియమం ప్రకారం t = – 273° C ను ఈ క్రింది సమీకరణంలో ప్రతిక్షేపించగా

• ఇచ్చట ఘనపరిమాణం సున్నా అగును.
• కావున ఆ వాయువు ఉనికి లేదు.
• అన్ని వాయువులు ఈ ఉష్ణోగ్రత ముందే ద్రవీకరింపబడతాయి.

ప్రశ్న 27.
కార్బన్ డైఆక్సైడ్, మిథేన్ల సందిగ్ధ ఉష్ణోగ్రతలు వరుసగా 31.1°C, – 81.9°C అయినా, వీటిలో ఏ వాయువులో బలమైన అంతరఅణు ఆకర్షణ బలాలుంటాయి?
సాధన:
CO₂ యొక్క సందిగ్ధ ఉష్ణోగ్రత T_C(CO₂) = 31.1° C
CH₄ యొక్క సందిగ్ధ ఉష్ణోగ్రత T_C(CH₄) = – 81.9° C
→ ఏ వాయువుకు అయితే అధిక సందిగ్ధ ఉష్ణోగ్రతను కలిగి యుండునో ఆ వాయువు నందు అంతర అణుబలాలు పెరిగి త్వరగా ద్రవీకరింపబడును.
∴ కావున CO₂ వాయువు త్వరగా ద్రవీకరింపబడును.

ప్రశ్న 28.
గాలిని 25°C నుండి 0°C కు చల్లబరిచిన, అణువుల rms వేగంలో కలిగే తగ్గుదలను లెక్కకట్టండి.
సాధన:


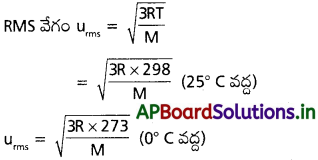
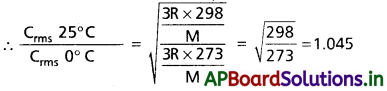
1.045 యూనిట్ల నందు 0.045 తగ్గుదల గలదు
100 యూనిట్ల నందు – \(\frac{100}{1.045}\) × 0.045 = 4.3 %
rms వేగంలో తగ్గుదల = 4.3 % (సుమారుగా)

ప్రశ్న 29.
27°c వద్ద 50, వాయువు RMS వేగం, సగటు వేగం, గరిష్ఠ సంభావ్యతా వేగాలను కనుక్కోండి.
సాధన:

ప్రశ్న 30.
27°C వద్ద 0, RMS, సగటు, గరిష్ఠ సంభావ్యతా వేగాలను కనుక్కోండి.
సాధన:

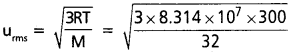
= 4.835 × 10⁴ cm/sec
T = 27° C = 300 K
M = 32 (O₂)
u_{(సగటు)} = 0.9213 × u_rms
= 0.9213 × 4.835 × 10⁴
= 4.455 × 10⁴ cm/sec.
u_mp = 0.8166 × u_rms
= 3.948 × 10⁴ cm/sec.

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
ఒక బెలూన్ గది ఉష్ణోగ్రత వద్ద హైడ్రోజన్ వాయువుతో నింపారు. పీడనం 0.2 bar కంటే ఎక్కువయితే బెలూన్ పగిలిపోతుంది. 1 bar పీడనం వద్ద వాయువు ఆక్రమించే ఘనపరిమాణము 2.27 L అయితే ఎంత ఘనపరిమాణం వరకు బెలూన్ను వ్యాకోచింపచేయవచ్చు.
సాధన:
బాయిల్ నియమం ప్రకారం p₁V₁ = p₂V₂
p₁ = 1 bar, అయితే V₁ = 2.27 L

1.2 బార్ పీడనం వద్ద బెలూన్ పగిలిపోతుంది. కాబట్టి బెలూన్ ఘనపరిమాణం 11.35 కంటే తక్కువ ఉండాలి.

ప్రశ్న 2.
23.4° C ఉష్ణోగ్రత వద్ద పసిఫిక్ మహాసముద్రంలో ప్రయాణిస్తున్న ఓడలో 2 L గాలితో నింపిన బెలూన్ ఉంది. ఆ ఓడ 26.1° C ఉష్ణోగ్రత వద్ద నున్న హిందూ మహాసముద్రం చేరుకొన్నప్పుడు, బెలూన్ ఘనపరిమాణం ఎంత ఉంటుంది?
సాధన:

ప్రశ్న 3.
25° C, 760 mm పాదరసం పీడనం వద్ద ఒక వాయువు 600 mL ఘనపరిమాణాన్ని ఆక్రమి స్తుంది. ఉష్ణోగ్రత 10° C వద్ద దాని ఘనపరిమాణం 640 mL ఉంటే, ఆ వాయువు పీడనం ఎంత ?
సాధన:
p₁ = 760 mm (పాదరసపు పీడనం), V₁ = 600 mL

ప్రశ్న 4.
360 cm³ మిథేన్ వాయువు 15 నిమిషాల్లో ఒక సచ్ఛిద్ర పాత్ర నుండి వ్యాపనం చెందింది. అదే పరిస్థితుల్లో 120 cm³ ఒక వాయువు 10 నిమిషాల్లో వ్యాపనం చెందినట్లయితే ఆ వాయువు మోలార్ ద్రవ్యరాశిని కనుక్కోండి.
సాధన:
మిథేన్ (CH₄) వాయువు
మిథేన్ వాయువు వ్యాపనం రేటు

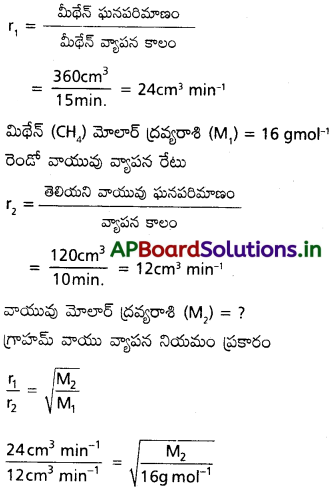
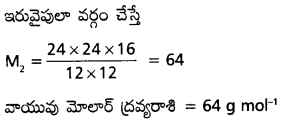
ప్రశ్న 5.
కార్బన్ డయాక్సైడ్, మరొక వాయువు ‘X’ ల వ్యాపనం రేట్లు వరుసగా 0.290cc s^-1, 0.271 cc s^-1 అయితే, ‘X’ వాయువు బాష్ప సాంద్రత కనుక్కోండి. కార్బన్ డయాక్సైడ్ బాష్ప సాంద్రత 22.
సాధన:

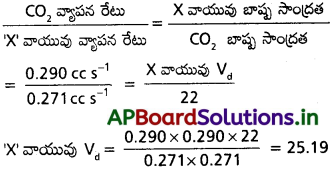
ప్రశ్న 6.
70.6g డై ఆక్సిజన్, 167.5 g నియాన్ వాయువులు గల వాయు మిశ్రమం కలుగజేసే పీడనం 25 bar. అయితే డై ఆక్సిజన్, నియాన్ వాయువుల పాక్షిక పీడనాలను కనుక్కోండి.
సాధన:

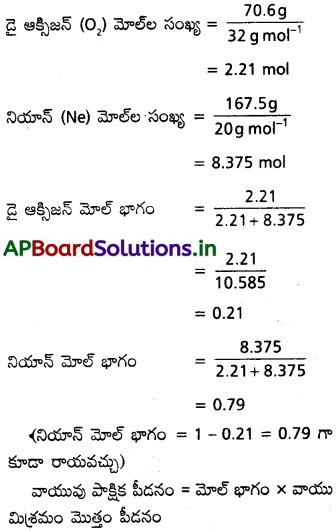
ప్రశ్న 7.
27° C వద్ద CO₂ వాయువు RMS, సగటు, గరిష్ఠ సంభావ్యత వేగాలను కనుక్కోండి.
సాధన:
T = 27 + 273 = 300 K ;
R = 8.314 J mol^-1K^-1
M = CO₂ మోలార్ ద్రవ్యరాశి = 44g mol^-1.

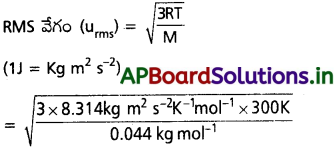
= 4.12 × 10²m s^-1
సగటు వేగం (u) = 0.9213 × RMS వేగం
= 0.9213 × 4.12 × 10²m s^-1
= 3.8 × 10² m s^-1

గరిష్ఠ సంభావ్యత వేగం
(u_mp) = 0.8166 × 4.12 × 10²m s^-1
= 3.36 × 10²m s^-1.

ప్రశ్న 8.
27° C వద్ద 5 మోల్ల డైనైట్రోజన్ వాయువు గతిజశక్తిని కనుక్కోండి.
సాధన:
గతిజశక్తి = \(\frac{3}{2}\)nRT
n = 5 మోల్లు; R = 8.314 J mol^-1 k^-1
T = 27° C + 273 = 300 K
గతిజశక్తి
E_k = \(\frac{3}{2}\) × 5 mol × 8.314 Jmol^-1 K^-1 × 300 K
= 18706.50 J

ప్రశ్న 9.
– 73°C వద్ద 4g. మిథేన్ వాయువు గతిజశక్తిని కనుక్కోండి.
సాధన:

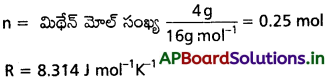
T = -73°C + 273 = 200 K
గతిజశక్తి (E) = \(\frac{3}{2}\) nRT
= \(\frac{3}{2}\) × 0.25 mol × 8.314 J mol^-1 K^-1 × 200 K
= 623.6 J.

ప్రశ్న 10.
ఒకే ఉష్ణోగ్రత వద్ద ఉన్న 3g H₂, 4g O₂ వాయువుల గతిజశక్తి నిష్పత్తిని లెక్కకట్టండి.
సాధన:
రెండు వాయువులు ఒకే ఉష్ణోగ్రత వద్ద ఉన్నాయి. కాబట్టి వాటి గతిజశక్తుల నిష్పత్తి వాటి మోల్ సంఖ్యల నిష్పత్తికి సమానం అవుతుంది. H₂, O₂ గతిజశక్తుల నిష్పత్తి
H₂ మోల్ : O₂ మోల్

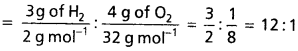
ప్రశ్న 11.
వాయువుల అభిలాక్షణిక ధర్మమైన సందిగ్ధ ఉష్ణోగ్రత వాయు అణువుల మధ్య ఉండే అంతర అణు ఆకర్షణ బలాల పరిమాణంపై ఆధారపడి ఉంటుంది. అమ్మోనియా, కార్బన్ డైఆక్సైడ్ వాయువులు సందిగ్ధ ఉష్ణోగ్రతలు వరసగా 405.5 K, 304.10 K. 500 K నుండి సందిగ్ధ ఉష్ణోగ్రతకు చల్లబరిచినపుడు వీటిలో ఏ వాయువు ముందుగా ద్రవీకరించబడుతుంది?
సాధన:
అమ్మోనియా వాయువు ముందుగా ద్రవీకరించబడు తుంది. దీనికి కారణం దాని సందిగ్ధ ఉష్ణోగ్రత ముందుగా వస్తుంది. CO₂ ద్రవీకరణకు అధిక చల్లదనం అవసరం.