AP Inter 2nd Year Maths 2A Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Ex 1(c)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(c)

అభ్యాసం 1(సి)

I.

ప్రశ్న 1.
క్రింది సంకీర్ణ సంఖ్యలను మాప – ఆయామ రూపంలో వ్యక్తపరచండి.
(i) 1 – i
సాధన:
1 – i = r(cos θ + i sin θ) అనుకుందాం.
ఇరువైపులా వాస్తవ సంకీర్ణ భాగాలను పోల్చగా
r cos θ = 1
r sin θ = -1
⇒ θ నాల్గవ పాదంలో ఉంది.
వర్గం చేసి కలుపగా
r²(cos²θ + sin²θ) = 1 + 1 = 2
r² = 2
⇒ r = √2
tan θ = -1 ⇒ θ = π/4
∴ 1 – i = \(\sqrt{2}\left(\cos \left(-\frac{\pi}{4}\right)+i \sin \left(-\frac{\pi}{4}\right)\right)\)

(ii) 1 + i√3 [Mar. ’14]
సాధన:
1 + i√3 = r(cos θ + i sin θ)
r cos θ = 1 …….(1)
r sin θ = √3 ……..(2)
θ మొదటి పాదంలో ఉంది.
వర్గం చేసి (1), (2) లను కలుపగా
r²(cos²θ + sin²θ) = 1 + 3
r² = 4
⇒ r = 2
(2) ను (1) చే భాగించగా
\(\frac{r \sin \theta}{r \cos \theta}\) = √3
tan θ = √3
⇒ θ = \(\frac{\pi}{3}\)
∴ 1 + i√3 = 2 (cos\(\frac{\pi}{3}\) + i sin\(\frac{\pi}{3}\))

(iii) -√3 + i
సాధన:
-√3 + i = r(cos θ + i sin θ) అనుకుందాం.
r cos θ = -√3 …..(1)
r sin θ = 1 ……..(2)
⇒ θ రెండో పాదంలో ఉంది.
వర్గం చేసి (1), (2) లను కలుపగా
r²(cos²θ + sin²θ) = 3 + 1 = 4
r² = 4
⇒ r = 2
(2) ను (1) చే భాగించగా
\(\frac{r \sin \theta}{r \cos \theta}=-\frac{1}{\sqrt{3}}\)
tan θ = \(-\frac{1}{\sqrt{3}}\), θ రెండో పాదంలో ఉంది కనుక
θ = 180° – 30° = 150° = \(\frac{5 \pi}{6}\)
∴ -√3 + i = 2(cos \(\frac{5 \pi}{6}\) + i sin \(\frac{5 \pi}{6}\))

(iv) -1 – i√3
సాధన:
-1 – i√3 = r(cos θ + i sin θ)
వాస్తవ, సంకీర్ణ భాగాలను పోల్చగా
r cos θ = -1, r sin θ = -√3
వర్గం చేసి కలుపగా
r²(cos²θ + sin²θ) = 1 + 3
r² = 4
⇒ r = 2

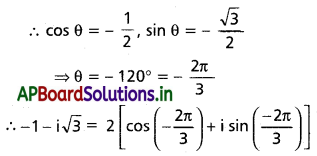
ప్రశ్న 2.
-2i(3 + i) (2 + 4i) (1 + i) ను సూక్ష్మీకరించి, ఆ సంకీర్ణ సంఖ్య మాపాన్ని రాబట్టండి.
సాధన:
-2i(3 + i) (2 + 4i) (1 + i)
= (-6i – 2i²) (2 + 2i + 4i + 4i²)
= (2 – 6i) (-2 + 6i)
= -4 + 12 – 36i² + 12i
= 32 + 24i
= 8(4 + 3i)
మాపం = |8(4 + 3i)| = \(8 \sqrt{(4)^2+(3)^2}\)
= 8(5)
= 40

ప్రశ్న 3.
(i) z ≠ 0 అయితే Arg z + Arg \(\overline{\mathbf{Z}}\) ను కనుక్కోండి.
సాధన:

(ii) z₁ = -1, z₂ = -i అయితే Arg(z₁z₂) ను కనుక్కోండి.
సాధన:
z₁ = -1 = cos π + i sin π
⇒ Arg z₁ = π
z₂ = -i = \(\cos \left(-\frac{\pi}{2}\right)+i \sin \left(-\frac{\pi}{2}\right)\)
⇒ Arg z₂ = -π/2
Arg(z₁z₂) = Arg z₁ + Arg z₂
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)

(iii) z₁ = -1, z₂ = i అయితే \({Arg}\left(\frac{z_1}{z_2}\right)\) ను కనుక్కోండి. [T.S. Mar ’16, May ’11]
సాధన:
z₁ = -1 = cos π + i sin π
⇒ Arg z₁ = π
z₂ = i = cos\(\frac{\pi}{2}\) + i sin\(\frac{\pi}{2}\)
⇒ Arg z₂ = \(\frac{\pi}{2}\)
\({Arg}\left(\frac{z_1}{z_2}\right)\) = Arg z₁ – Arg z₂
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)

ప్రశ్న 4.
(i) (cos 2α + i sin 2α) (cos 2β + i sin 2β) = cos θ + i sin θ అయితే θ విలువను కనుక్కోండి.
సాధన:
cos θ + i sin θ = (cos 2α + i sin 2α) (cos 2β + i sin 2β)
= cos 2α . cos 2β + i sin 2α . cos 2β + i cos 2α sin 2β + i² sin 2α . sin 2β
= (cos 2α . cos 2β – sin 2α . sin 2β) + i(sin 2α cos 2β + cos 2α sin 2β)
= cos 2(α + β) + i . sin 2(α + β)
∴ θ = 2(α + β)

(ii) √3 + i = r (cos θ + i sin θ), అయితే θ విలువను రేడియన్లలో కనుక్కోండి.
సాధన:
∴ √3 + i = r(cos θ + i sin θ)
⇒ r cos θ = √3, r sin θ = 1
⇒ r²(cos²θ + sin²θ) = 3 + 1
⇒ r² = 4
⇒ r = 2
∴ cos θ = \(\frac{\sqrt{3}}{2}\), sin θ = \(\frac{1}{2}\)
⇒ θ = \(\frac{\pi}{6}\)

(iii) x + iy = cis α . cis β and x² + y² విలువను కనుక్కోండి.
సాధన:
x + iy = cis α . cis β
⇒ x + iy = (cos α + i sin α) (cos β + i sin β)
⇒ x + iy = cos(α + β) + i sin(α + β)
వాస్తవ భాగాలను, సంకీర్ణ భాగాలను పోల్చిన
x = cos(α + β), y = sin(α + β)
∴ x² + y² = cos²(α + β) + sin²(α + β) = 1

(iv) \(\frac{z_2}{z_1}\), (z₁ ≠ 0) ఒక శుద్ధ కల్పిత సంఖ్య అయితే, \(\left|\frac{2 z_1+z_2}{2 z_1-z_2}\right|\) విలువను కనుక్కోండి.
సాధన:

(v) (√3 + i)¹⁰⁰ = 2⁹⁹ (a + ib) అయితే a² + b² = 4 అని చూపండి. [A.P Mar ’16]
సాధన:

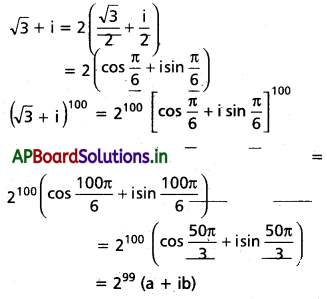
ప్రశ్న 5.
(i) z = x + iy, |z| = 1 అయితే z బిందుపథాన్ని కనుక్కోండి.
సాధన:
|z| = 1
\(\sqrt{x^2+y^2}\) = 1
⇒ x² + y² = 1
z బిందుపథం x² + y² = 1

(ii) (z – 1) యొక్క ఆయామం \(\frac{\pi}{2}\) అయితే, z యొక్క బిందుపథాన్ని కనుక్కోండి. [May ’07]
సాధన:
z – 1 = x + iy – 1 = (x – 1) + iy
(z – 1) ఆయామం \(\frac{\pi}{2}\) కావున
వాస్తవ భాగం శూన్యం
⇒ x – 1 = 0
∴ z బిందుపథం x – 1 = 0

(iii) Arg \(\overline{\mathbf{z}}_1\), Arg z₂ లు వరుసగా \(\frac{\pi}{5}, \frac{\pi}{3}\) అయితే (Arg z₁ + Arg z₂) ను కనుక్కోండి. [A.P Mar ’16]
సాధన:

(iv) z = \(\frac{1+2 i}{1-(1-i)^2}\) అయితే Arg(z) ను కనుక్కోండి.
సాధన:

II.

ప్రశ్న 1.
క్రింది సంకీర్ణ సంఖ్యలను సూక్ష్మీకరించి, వాటి మాపాన్ని కనుక్కోండి.
(i) \(\frac{(2+4 i)(-1+2 i)}{(-1-i)(3-i)}\)
(ii) \(\frac{(1+i)^3}{(2+i)(1+2 i)}\)
సాధన:

ప్రశ్న 2.
(i) (1 – i) (2 – i) (3 – i)…. (1 – ni) = x – iy, అయితే 2.5.10 …. (1 + n²) = x² + y² అని చూపండి.
సాధన:

(ii) \(\frac{z+1}{z+i}\) యొక్క వాస్తవ భాగం 1 అయితే z యొక్క బిందుపథాన్ని కనుక్కోండి.
సాధన:

(iii) |z – 3 + i| = 4 అయితే z బిందుపథాన్ని నిర్ధారించండి. [Mar. ’14; May ’08]
సాధన:
|z – 3 + i| = 4
|x + iy – 3 + i = 4
(x – 3) + (y + 1)| = 4
\(\sqrt{(x-3)^2+(y+1)^2}\) = 4
∴ z బిందుపథం (x – 3)² + (y + 1)² = 16
x² – 6x + 9 + y² + 2y + 1 – 16 = 0
x² + y² – 6x + 2y – 6 = 0

(iv) |z + ai| = |z – ai| అయితే z బిందుపథాన్ని కనుక్కోండి.
సాధన:
|z + ai| = |z – ai|
|x + iy + ai| = |x + iy – ai|
|x + i(y + a)| = |x + i(y – a)|
\(\sqrt{x^2+(y+a)^2}=\sqrt{x^2+(y-a)^2}\)
x² + (y + a)² = x² + (y – a)²
(y + a)² – (y – a)² = 0
i.e., 4ay = 0
⇒ y = 0
z బిందుపథం y = 0

ప్రశ్న 3.
z = x + iy అయి, P బిందువు ఆర్గాండ్ తలంలో z ని సూచిస్తుంటే, క్రింది సమీకరణాలను తృప్తిపరచే, z బిందు పథాన్ని కనుక్కోండి.
(i) |2z – 3| = 7
సాధన:
|2z – 3| = 7
z = x + iy
⇒ |2z – 3| = 7
⇒ |2(x + iy) – 3| = 7
⇒ (2x – 3) + 2(iy)| = 7
⇒ \(\sqrt{(2 x-3)^2+4 y^2}\) = 7
P బిందుపథం (2x – 3)² + 4y² = 49
⇒ 4x² + 9 – 12x + 4y² – 49 = 0
⇒ 4x² + 4y² – 12x – 40 = 0
(i.e,) x² + y² – 3x – 10 = 0
∴ z యొక్క బిందుపథం x² + y² – 3x – 10 = 0
ఈ సమీకరణం వృత్తాన్ని సూచిస్తుంది.
కేంద్రం = (\(\frac{3}{2}\), 0)
వ్యాసార్ధం = \(\sqrt{\frac{9}{4}-(-10)}\)
= \(\sqrt{\frac{9+40}{4}}\)
= \(\frac{7}{2}\) యూనిట్లు

(ii) z² = 4 Re (z + 2)
సాధన:
z = x + iy, |z|² = 4 Re (z + 2)
⇒ |x + iy|² = 4 Re (x + iy + 2)
⇒ \(\left(\sqrt{x^2+y^2}\right)^2\) = 4 Re (x + 2 + iy)
⇒ (x² + y²) = 4(x + 2)
⇒ x² + y² – 4x – 8 = 0
ఇదియే P బిందుపథం.
ఈ సమీకరణం వృత్తాన్ని సూచిస్తుంది.
కేంద్రం = (2, 0)
వ్యాసార్థం = \(\sqrt{4-(-8)}\) = √12 = 2√3 యూనిట్లు

(iii) |z + i|² – |z – i|² = 2
సాధన:
z = x + iy
|z + i|² – |z – i|² = 2
⇒ |x + iy + i|2 – |x + iy – i|2 = 2
⇒ x + i(y + 1)2 – |x + (y – 1)|2 = 2
⇒ \(\left[\sqrt{x^2+(y+1)^2}\right]^2-\left[\sqrt{x^2+(y-1)^2}\right]^2\) = 2
⇒ x² + (y + 1)² – (x² + (y – 1)²) = 2
⇒ (y + 1)² – (y – 1)² = 2
⇒ 4y = 2
⇒ 2y = 1
P బిందుపథం 2y – 1 = 0
ఈ సమీకరణం X- అక్షానికి సమాంతరంగా గల సరళరేఖ.

(iv) |z + 4i| + |z – 4i| = 10
సాధన:
z = x + iy
∵ |z + 4i| + |z – 4i| = 10
⇒ |x + iy + 4i| + |x + iy – 4i| = 10
⇒ |x + i(y + 4)| + |x + (y – 4)i| = 10
⇒ \(\sqrt{x^2+(y+4)^2}+\sqrt{x^2+(y-4)^2}\) = 10
⇒ \(\sqrt{x^2+(y+4)^2}=10-\sqrt{x^2+(y-4)^2}\)
ఇరువైపులా వర్గం చేయగా
⇒ x² + (y + 4)² = \(\left[10-\sqrt{x^2+(y-4)^2}\right]^2\)
⇒ x² + (y + 4)² = 100 + x² + (y – 4)² – 20\(\sqrt{x^2+(y-4)^2}\)
⇒ (y + 4)² – (y – 4)² – 100 = -20\(\sqrt{x^2+(y-4)^2}\)
⇒ 4 (y) (4) – 100 = -20\(\sqrt{x^2+(y-4)^2}\)
⇒ 4(4y – 25) = -20\(\sqrt{x^2+(y-4)^2}\)
⇒ (4y – 25) = -5\(\sqrt{x^2+(y-4)^2}\)
మరల వర్గం చేయగా (4y – 25)² = 25[x² + (y – 4)²]
16y² + 625 – 200y = 25x² + 25y² – 200y + 400
25x² + 9y² = 225
∴ P బిందుపథం 25x² + 9y² = 225
\(\frac{x^2}{9}+\frac{y^2}{25}=1\)
ఈ సమీకరణం దీర్ఘవృత్తాన్ని సూచిస్తుంది.
a² = 9, b² = 25
a² = b² (1 – e²)
⇒ 9 = 25 (1 – e²)
⇒ 1 – e² = \(\frac{9}{25}\)
e² = 1 – \(\frac{9}{25}\) = \(\frac{16}{25}\)
∴ ఉత్కేంద్రత = \(\frac{4}{5}\) మరియు దీర్ఘాక్షం y – అక్షానికి సమాంతరంగా ఉండును.

ప్రశ్న 4.
(i) z₁, z₂ లు రెండు శూన్యేతర సంకీర్ణ సంఖ్యలు మరియు |z₁ + z₂| = |z₁| + |z₂| అయితే Arg z₁ – Arg z₂ = 0 అని చూపండి.
సాధన:
z₁ + z₂ = (x₁ + iy₁) + (x₂ + iy₂) = (x₁ + x₂) + i(y₁ + y₂)
|z₁ + z₂| = \(\sqrt{\left(x_1+x_2\right)^2+\left(y_1+y_2\right)^2}\)
(దత్తాంశం నుండి) |z₁ + z₂| = |z₂| + |z₂|

(ii) z = x + iy ఆర్గాండ్ తలంలో P బిందువు z ని సూచిస్తుంది. \(\left|\frac{\mathbf{z}-\mathbf{a}}{\mathbf{z}+\overline{\mathbf{a}}}\right|\) = 1, వాస్తవ (a) ≠ 0 అయితే P బిందు
పథాన్ని కనుక్కోండి.
సాధన:
z = x + iy, a = α + iβ అనుకుందాం.

(x – α)² + (y – β)² = (x + α)² + (y – β)²
⇒ (x – α)² = (x + α)²
⇒ (x + α)² – (x – α)² = 0
⇒ 4αx = 0
Re(a) ≠ 0 ⇒ α ≠ 0
⇒ x = 0
∴ P బిందుపథం x = 0 i.e., Y-అక్షం.