Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(d) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(d)
అభ్యాసం – 1(డి)
I.
ప్రశ్న 1.
(i) ఆర్లాండ్ తలంలో 7 + 7i, 7 – 7i బిందువులను కలిపే రేఖాఖండపు లంబ సమద్విఖండన రేఖకు సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సంకీర్ణ సంఖ్యలు ఆర్లాండ్ తలంలో A(7, 7); B(7, -7) లను సూచిస్తున్నాయి అనుకుందాం.
AB మధ్యబిందువు O
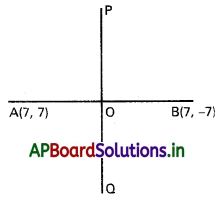
‘O’ నిరూపకాలు \(\left(\frac{7+7}{2}, \frac{7-7}{2}\right)\) = (7, 0)
\(\overleftrightarrow{\mathrm{AB}}\) వాలు = \(\frac{7+7}{7-7}=\frac{14}{0}\) = ∞
\(\overline{\mathrm{AB}}\) రేఖ అక్షానికి సమాంతరంగా ఉంది.
\(\overline{\mathrm{PQ}} \perp \overline{\mathrm{AB}}\)
\(\overleftrightarrow{\mathrm{PQ}}\) రేఖ X-అక్షానికి సమాంతరంగా ఉంది.
\(\overline{\mathrm{PQ}}\) వాలు = 0
\(\overrightarrow{\mathrm{PQ}}\) సమీకరణం y – 0 = 0(x – 7)
y = 0
(ii) ఆర్లాండ్ తలంలో (-9 + 6i), (11 – 4i) బిందువులను కలిపే సరళరేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
(-9 + 6i), (11 – 4i) లు ఆర్లాండ్ తలంలో సూచించే బిందువులు. (-9, 6), B(11, -4).
\(\overleftrightarrow{\mathrm{AB}}\) రేఖా సమీకరణం
⇒ y – y1 = \(\left(\frac{y_2-y_1}{x_2-x_1}\right)\) (x – x1)
⇒ y – 6 = \(\left(\frac{-4-6}{11+9}\right)\) (x + 9)
⇒ y – 6 = \(-\frac{1}{2}\)(x + 9)
⇒ 2y – 12 = -x – 9
⇒ x + 2y – 3 = 0
![]()
ప్రశ్న 2.
z = x + iy అవుతూ, P బిందువు ఆర్గాండ్ సమతలంలో z ను సూచిస్తుంటే, క్రింది సమీకరణాలను తృప్తిపరచే z బిందుపథాన్ని కనుక్కోండి.
(i) |z – 2 – 3i| = 5
సాధన:
z = x + iy, |z – 2 – 3i| = 5
|z – 2 – 3i| = 5
⇒ \(|x+i \overline{y-2}-3 i|=5\)
⇒ |(x – 2) + (y – 3)| = 5
⇒ \(\sqrt{(x-2)^2+(y-3)^2}=5\)
⇒ (x – 2)2 + (y – 3)2 = 25
⇒ x2 – 4x + 4 + y2 – 6y + 9 = 25
∴ P బిందుపథం x2 + y2 – 4x – 6y – 12 = 0
(ii) 2|z – 2| = |z – 1|
సాధన:
2|z – 2| = |z – 1|
⇒ 2|x + iy – 2| = |x + iy – 1|
⇒ 2(x – 2) + iy| = |(x – 1) + iy|
⇒ \(2 \sqrt{(x-2)^2+y^2}=\sqrt{(x-1)^2+y^2}\)
ఇరువైపులా వర్గం చేయగా
⇒ 4[(x – 2)2 + y2] = (x – 1)2 + y2
⇒ 4(x2 – 4x + 4 + y2) = x2 – 2x + 1 + y2
⇒ 4x2 + 4y2 – 16x + 16 = x2 + y2 – 2x + 1
∴ P బిందుపథం 3x2 + 3y2 – 14x + 15 = 0
(iii) Img z2 = 4
సాధన:
Img z2 = 4
∵ z = x + iy
⇒ z2 = (x + iy)2 = x2 + i2y2 + 2ixy = (x2 – y2) + i(2xy)
∴ Img (z2) = 2xy = 4
∴ P బిందుపథం xy = 2
(iv) \({Arg}\left|\frac{z-1}{z+1}\right|=\frac{\pi}{4}\)
సాధన:


ప్రశ్న 3.
ఆర్లాండ్ సమతలంలో 2 + 2i, -2 – 2i, 2√3 + 2√3i లను సూచించే బిందువులతో ఏర్పడే త్రిభుజం సమబాహు త్రిభుజమని చూపండి. (May ’07)
సాధన:
ఇచ్చిన సంకీర్ణ సంఖ్యలు ఆర్గాండ్ తలంలో A(2, 2), B(-2, -2), C(-2√3, 2√3) లను సూచిస్తున్నాయి అనుకుందాం.
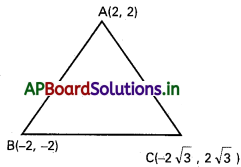
AB2 = (2 + 2)2 + (2 + 2)2
= 16 + 16
= 32
BC2 = (-2 + 2√3)2 + (-2 – 2√3)2
= 4 + 12 – 8√3 + 4 + 12 + 8√3
= 32
AC2 = (-2√3 – 2)2 + (2√3 – 2)2
= 12 + 4 + 8√3 +12 +4 – 8√3
= 32
AB2 = BC2 = AC2
⇒ AB = BC = CA
∴ ∆ABC సమబాహు త్రిభుజంను సూచిస్తుంది.
![]()
ప్రశ్న 4.
|z – 4| + \(\left|z-\frac{12}{5}\right|\) = 10 సమీకరణం ద్వారా సూచించే దీర్ఘవృత్త యొక్క ఉత్కేంద్రతను కనుక్కోండి.
సాధన:
SP + S’P = 2a
S = (4, 0)
S’ = (\(\frac{12}{5}\), 0)
2a = 10
a = 5
SS’ = 2ae
4 – \(\frac{12}{5}\) = 2 × 5e
\(\frac{8}{5}\) = 10e
e = \(\frac{4}{25}\)
II.
ప్రశ్న 1.
\(\frac{z_3-z_1}{z_2-z_1}\) ఒక వాస్తవ సంఖ్య అయినప్పుడు z1, z2, z3 సంకీర్ణ సంఖ్యలను సూచించే బిందువులు సరేఖీయాలని చూపండి.
సాధన:
z1 = x1 + iy1, z2 = x2 + iy2, z3 = x3 + iy3 అనుకుందాం.

\(\frac{z_3-z_1}{z_2-z_1}\) ఒక వాస్తవ సంఖ్య కనుక దాని సంకీర్ణ భాగం సున్నా కావాలి.
⇒ (y3 – y1) (x2 – x1) – (x3 – x1) (y2 – y1) = 0
⇒ (y3 – y1) (x2 – x1) = (x3 – x1) (y2 – y1)
\(\frac{y_3-y_1}{x_3-x_1}=\frac{y_2-y_1}{x_2-x_1}\)
A(x1, y1), B(x2, y2), C(x3, y3) బిందువులు
z1, z2, z3 లను సూచిస్తున్నాయి.
\(\stackrel{\leftrightarrow}{\mathrm{AC}}\) వాలు = \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) వాలు
∴ A, B, C లు సరేఖీయాలు.
ప్రశ్న 2.
2 + i, 4 + 3i, 2 + 5i, 3i అనే సంకీర్ణ సంఖ్యలను సూచించే బిందువులు, ఆర్గాండ్ సమతలంలో ఒక చతురస్ర శీర్షాలను తెలుపుతాయని చూపండి.
సాధన:
A(2, 1), B(4, 3), C(2, 5), D(0, 3) లు ఆర్లాండ్ సమతలంలో దత్త సంకీర్ణ సంఖ్యలను సూచించే బిందువులు.
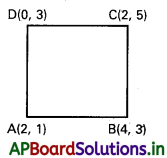
AB2 = (2 – 4)2 + (1 – 3)2 = 4 + 4 = 8
BC2 = (4 – 2)2 + (3 – 5)2 = 4 + 4 = 8
CD2 = (2 – 0)2 + (5 – 3)2 = 4 + 4 = 8
DA2 = (0 – 2)2 + (3 – 1)2 = 4 + 4 = 8
AB2 = BC2 = CD2 = DA2
⇒ AB = BC = CD = DA …..(1)
AC2 = (2 – 2)2 + (1 – 5)2 = 0 + 16 = 16
BD2 = (4 – 0)2 + (3 – 3)2 = 16 + 0 = 16
AC2 = BD2
⇒ AC = BD …….(2)
(1), (2) ల నుంచి A, B, C, D లు చతురస్రం శీర్షాలు.
![]()
ప్రశ్న 3.
-2 + 7i, \(-\frac{3}{2}+\frac{1}{2}\), 4 – 3i, \(\frac{7}{2}\)(1 + i) అనే సంకీర్ణ సంఖ్యలను సూచించే బిందువులు, ఆర్ఖండ్ తలంలో ఒక సమచతుర్భుజి (రాంబస్) శీర్షాలను సూచిస్తాయని నిరూపించండి. [T.S. Mar ’16, May ’05, Mar. ’05, June ’04]
సాధన:


AC ≠ BD …..(2)
కనుక A, B, C, D లు సమచతుర్భుజి (రాంబస్) శీర్షాలు.
ప్రశ్న 4.
ఆర్గాండ్ తలంలో z1, z2, z3 సంకీర్ణ సంఖ్యలను సూచించే బిందువులు సరేఖీయాలు కావడానికి ఆవశ్యక, పర్యాప్త నియమం pz1 + qz2+ rz3 = 0, p + q + r = 0 లను తృప్తి పరచే అన్ని శూన్యం కాని మూడు వాస్తవ సంఖ్యలు p, q, r లు వ్యవస్థితం అని చూపండి. [Mar. ’07]
సాధన:
pz1 + qz2 + rz3 = 0
⇔ rz3 = -pz1 – qz2
⇔ z3 = \(\frac{-p z_1-q z_2}{r}\)
∵ r ≠ 0
∵ p + q + r = 0
⇔ r = -p – q
⇔ z3 = \(-\frac{\left(p z_1+q z_2\right)}{-(p+q)}\)
⇔ z3 = \(\frac{p z_1+q z_2}{p+q}\)
⇔ z3, z1, z2 లను కలిపే రేఖాఖండాన్ని q : p నిష్పత్తిలో విభజిస్తుంది.
⇔ z1, z2, z3 లు సరేఖీయాలు.
![]()
ప్రశ్న 5.
ఆర్గాండ్ సమతలంలో P, Q బిందువులు z1, z2 సంకీర్ణ సంఖ్యలను సూచిస్తున్నాయి. O మూల బిందువు \(z_1 \bar{z}_2+\bar{z}_1 z_2=0\) అయినప్పుడు ∠POQ = 90° అని చూపండి. [Mar. ’07]
సాధన:
z1 = x1 + iy1, z2 = x2 + iy2 అనుకుంటే,
అప్పుడు P(x1, y1), Q(x2, y2), O(0, 0) లు అవుతాయి.

ప్రశ్న 6.
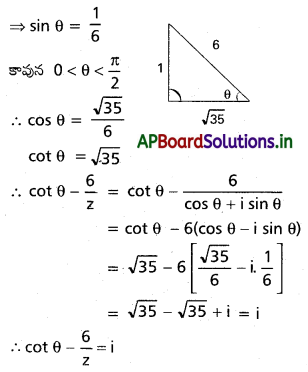
సంకీర్ణ సంఖ్య z ఆయామం θ, 0 < θ < \(\frac{\pi}{2}\) ని కలిగి, అది |z – 3i| = 3 సమీకరణాన్ని తృప్తిపరిస్తే (cot θ – \(\frac{6}{z}\)) = i అని చూపండి.
సాధన:
z = cos θ + i sin θ అనుకొనుము.
ఇచ్చినది |z – 3i| = 3
⇒ |(cos θ + i sin θ) – 3i| = 3
⇒ |cos θ + i(sin θ – 3)| = 3
⇒ \(\sqrt{\cos ^2 \theta+(\sin \theta-3)^2}\) = 3
⇒ cos2θ + sin2θ – 6 sin θ + 9 = 9
⇒ 1 – 6 sin θ = 0
⇒ 6 sin θ = 1