AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Ex 1(b)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 1 వృత్తం Exercise 1(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Exercise 1(b)

అభ్యాసం – 1(బి)

I.

ప్రశ్న 1.
కింద ఇచ్చిన వృత్తం దృష్ట్యా ఇచ్చిన బిందువు స్థితిని తెలపండి.
i) S ≡ x² + y² – 4x – 6y – 12 = 0; P(3, 4)
సాధన:
S ≡ x² + y² – 4x-6y – 12
P(3, 4) = (x₁, y₁)
S₁₁ = 3² +4² – 4.3 – 6.4 – 12
= 9 + 16 – 12 – 24 – 12
= -23 < 0
P (3, 4) వృత్తానికి అంతరంగా ఉంది.

ii) S ≡ x² + y² – 2x-4y + 3 = 0; P(1, 5) 3.
సాధన:
S₁₁ ≡ (1)² + (5)² – 2(-1) – 4(5) + 3 = 7
S₁₁ > 0 కనుక P వృత్తానికి వెలుపల ఉంది.

iii) S ≡ 2x² + 2y² – 5x – 4y – 3 = 0; P (4, 2)
సాధన:
S₁₁ ≡2(4)² + 2(2)² – 5(4) – 4(2) – 3 = 9
S₁₁ > 0 కనుక P వృత్తానికి వెలుపల ఉంది.

iv) S ≡ x² + y² – 2x – 4y + 3 = 0; P(2, -1)
సాధన:
S₁₁ ≡ (2)2 + (-1)² – 2(2) – 4 (-1) + 3 = 8
S₁₁ > 0 కనుక P వృత్తానికి వెలుపల ఉంది.

ప్రశ్న 2.
క్రింద ఇచ్చిన ప్రతి వృత్తంS = 0 దృష్ట్యా P బిందు శక్తి కనుక్కోండి.
i) S ≡ x² + y² + 8x + 12y + 15; P = (5, -6)
సాధన:
S₁₁ ≡ బిందు శక్తి
25 + 36 + 40 -7 2 +15 = 116 – 72 = 44

ii) S ≡ x² + y² – 6x + 4y – 12 ; P = (1, 1) [T.S. Mar. ’16]
సాధన:
బిందు శక్తి = S₁₁ = 1 + 1 + 6 + 4 – 12 = 0

iii) S ≡ x² + y² – 2x + 8y – 23 ; P = (2, 3)
సాధన:
బిందు శక్తి = S₁₁ = 4 + 9 – 4 + 24 – 23 = 10.

iv) S ≡ x² + y² – 4x – 6y – 12 ; P = (2, 4)
సాధన:
బిందు శక్తి = 4 + 16 – 8 – 24 – 12 = -24.

ప్రశ్న 3.
కింద ఇచ్చిన బిందువు P నుంచి 5 = 0 వృత్తానికి గల స్పర్శరేఖ పొడవును కనుక్కోండి.
i) S ≡ x² + y² – 25; P = (-2, 5)
సాధన:
స్పర్శరేఖ పొడవు
= \(\sqrt{S_{11}}\)
= \(\sqrt{(-2)^2+(5)^2-25}\)
= 2 యూనిట్లు

ii) S ≡ x² + y² – 14x + 2y + 25 ; P = (0, 0)
సాధన:
స్పర్శరేఖ పొడవు = \(\sqrt{S_{11}}\)
= \(\sqrt{0+0-0+0+25}\)
= 5 యూనిట్లు.

iii) S ≡ x² + y² – 5x + 4y – 5; P = (2, 5)
సాధన:
స్పర్శరేఖ పొడవు = \(\sqrt{S_{11}}\)
= \(\sqrt{4+25-10+20-5}\)
= \(\sqrt{34}\) యూనిట్లు.

II.

ప్రశ్న 1.
బిందువు (5, 4) నుంచి x² + y² + 2ky = 0 వృత్తానికి గీసిన స్పర్శరేఖ పొడవు 1 అయితే k విలువను కనుక్కోండి. (Mar. ’01)
సాధన:
స్పర్శరేఖ పొడవు
= \(\sqrt{S_{11}}=\sqrt{(5)^2+(4)^2+8 k}\)
స్పర్శరేఖ పొడవు = 1 కనుక
∴ 1 = \(\sqrt{25+16+8 k}\)
వర్గీకరించగా 1 = 41 + 8k
k = 5 యూనిట్లు.

ప్రశ్న 2.
బిందువు (2, 5) నుంచి x² + y² – 5x + 4y + k = 0 కు గల స్పర్శరేఖ పొడవు 37 అయితే k విలువను కనుక్కోండి.
సాధన:
స్పర్శరేఖ పొడవు = \(\sqrt{S_{11}}\)
= \(\sqrt{(2)^2+(5)^2-5 \times 2+4 \times 5+k}\)
= 37 = 39 + k
k = – 2 యూనిట్లు.

III.

ప్రశ్న 1.
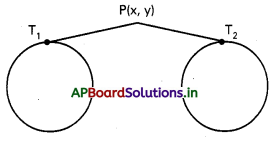
P బిందువు నుంచి x² + y² – 4x – 6y – 12 = 0, x² + y² + 6x + 18y + 26 = 0 వృత్తాలకు గీసిన స్పర్శరేఖల పొడవులు 2 : 3 నిష్పత్తిలో ఉంటే P బిందు పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
P(x, y) బిందు పధం మీది ఏదైనా ఒక బిందువు
S ≡ x² + y² – 4x – 6y – 12
PT₁ = \(\sqrt{x^2+y^2-4 x-6 y-12}\)
S¹ = x² + y² + 6x + 18y + 26
PT₂ = \(\sqrt{x^2+y^2+6 x+18 y+26}\)
\(\frac{\mathrm{PT}_1}{\mathrm{PT}_2}=\frac{2}{3}\) అని ఇవ్వబడినది.
⇒ \(\frac{\mathrm{PT}_1^2}{\mathrm{PT}_2^2}=\frac{4}{9}\)

9 PT₁² = 4.PT₁²
9(x² + y² – 4x – 6y – 12)
= 4(x² + y² + 6x + 18y + 26)
9x² + 9y² – 36x – 54y – 108
= 4x² + 4y² + 24x + 72y + 104
∴ P బిందు పథము
5x² + 5y² – 60x – 126y – 212 = 0

ప్రశ్న 2.
చలించే బిందువు P నుంచి x² + y² + 8x + 12y + 15 = 0, x² + y² – 4x – 6y – 12 = 0 వృత్తాలకు గీసిన స్పర్శరేఖల పొడవులు సమానం అయితే P యొక్క బిందు పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:

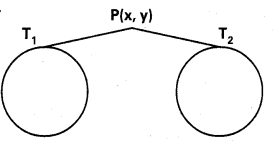
వృత్తాల సమీకరణాలు
S ≡ x² + y² + 8x + 12y + 15 = 0
S¹ = x² + y² – 4x – 6y – 12 = 0
P (x₁, y₁) బిందు పథం మీది బిందువు PT₁, PT₂ లు P నుండి వృత్తాలకు గీయబడిన స్వర్శరేఖలు
దత్త నియమము PT₁ = PT₂ ⇒ PT₁² = PT₂²
x₁² + y₁² + 8x₁ + 12y₁ + 15
= x₁² + y₁² – 4x₁ – 6y₁ – 12
12x₁ + 18y₁ + 27 = 0
(లేదా) 4x₁ + 6y₁ + 9 = 0
P(x₁, y₁) బిందు పథము 4x + 6y + 9 = 0