AP Inter 2nd Year Maths 2B Solutions Chapter 3 పరావలయం Ex 3(b)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 3 పరావలయం Exercise 3(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 3 పరావలయం Exercise 3(b)

అభ్యాసం – 3(బి)

I.

ప్రశ్న 1.
y² = 6x పరావలయానికి ధనాత్మక నాభి లంబాగ్రం వద్ద స్పర్శరేఖ, అభిలంబరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
(a, 2a) కాని 4a = 6 ⇒ a = \(\frac{3}{2}\)
(\(\frac{3}{2}\), 3)
స్పర్శరేఖ సమీకరణము yy₁ = 2a (x + x₁)
yy₁ = 3(x + x₁)
3y = 3(x + \(\frac{3}{2}\))
2y – 2x – 3 = 0 స్పర్శరేఖ సమీకరణము
స్పర్శరేఖ వాలు 1
అభిలంబరేఖ వాలు – 1
అభిలంబరేఖ సమీకరణం y – 3 = -1(x – \(\frac{3}{2}\))
2x + 2y – 9 = 0

ప్రశ్న 2.
x² – 4x 8y + 12 = 0 పరావలయంపై (4, \(\frac{3}{2}\)) వద్ద స్పర్శరేఖ, అభిలంబరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
(x – 2)² – 4 – 8y + 12 = 0
⇒ (x – 2)² – 8y + 8 = 0
⇒ (x – 2)² = 8(y – 1); 4a = 8 ⇒ a = 2
(x₁, y₁) వద్ద స్పర్శరేఖ సమీకరణము
(x – 2) (x₁ – 2) = 2a (y – 1 + y₁ – 1)
⇒ (x – 2) (4 – 2) = 2a (y – 1+ \(\frac{3}{2}\) – 1)
⇒ 2(x – 2) = 4\(\left(\frac{2 y-1}{2}\right)\)
x – 2y – 1 = 0
అభిలంబరేఖ సమీకరణము
y – y₁ = m(x – x₁) అనుకుందాం.
m – అభిలంబరేఖ వాలు
స్పర్శరేఖ వాలు \(\frac{1}{2}\)
అభిలంబ రేఖ వాలు – 2
అభిలంబరేఖ సమీకరణము
y – \(\frac{3}{2}\) = -2(x – 4)
2y – 3 = – 4x + 16
4x + 2y – 19 = 0

ప్రశ్న 3.
y² = 6x పరావలయానికి 2y = 5x + k స్పర్శరేఖ అయితే k విలువ కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
దత్తరేఖ 2y = 5x + k

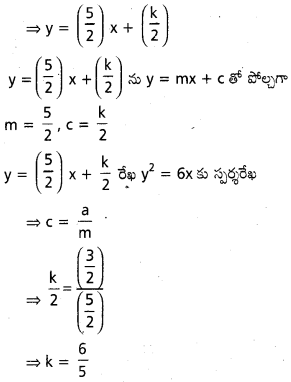
ప్రశ్న 4.
y² = 4x పరావలయానికి y – 2x + 5 = 0 రేఖకు సమాంతరంగా గల అభిలంబ రేఖసమీకరణం కనుక్కోండి.
సాధన: ప
రావలయము సమీకరణము y² = 4x
∴ a = 1
దత్తరేఖ సమీకరణము y – 2x + 5 = 0.
వాలు m = 2
అభిలంబ రేఖ y – 2x + 5 = 0 కు సమాంతరము
అభిలంబరేఖ వాలు = 2
రేఖా సమీకరణము ‘t’ వద్ద అభిలంబ
y + tx = 2at + at³
∴ Slope = -t = 2
⇒ t = -2
అభిలంబరేఖ సమీకరణము
y – 2x = 2.1 (-2) + 1(-2)
= -4 – 8 = -12
2x – y – 12 = 0.

ప్రశ్న 5.
y² = 16x పరావలయానికి 2x – y + 2 = 0 స్పర్శరేఖ అవుతుంది అని చూపి, స్పర్శబిందువు కనుక్కోండి.
సాధన:
దత్తరేఖ 2x – y + 2 = 0
⇒ y = 2x + 2
y = mx + c తో పోల్చగా m = 2, c = 2
y² = 16x ను y² = 4ax తో పోల్చగా
4a = 16 ⇒ a = 4
\(\frac{a}{m}=\frac{4}{2}\) = 2 = c
∴ స్పర్శబిందువు = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=\left(\frac{4}{2^2}, \frac{2(4)}{2}\right)\)
= (1, 4)

ప్రశ్న 6.
y² = 16x పరావలయానికి, X- అక్షంతో 60° కోణం చేసే స్వర్శలేఖ సమీకరణం కనుక్కోండి. స్వర్శ బిందువును కూడా కనుక్కోండి.
సాధన:
θ = 60°; m = tan 60° = \(\sqrt{3}\)
y = mx + \(\frac{a}{m}\)
y = \(\sqrt{3x}\) + \(\frac{4}{\sqrt{3}}\)
\(\sqrt{3y}\) = 3x + 4
స్పర్శబిందువు = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=\left(\frac{4}{3}, \frac{8}{\sqrt{3}}\right)\)

II.

ప్రశ్న 1.
y² = 16x పరావలయానికి సరళరేఖ 2x – y + 5 = 0 కు సమాంతరంగా ఉండే, లంబంగా ఉండే స్పర్శరేఖల సమీకరణాలు కనుక్కోండి. స్పర్శ బిందువులు నిరూపకాలు కనుక్కోండి.
సాధన:
పరావలయం సమీకరణము y² = 16x
స్పర్శరేఖ 2x – y + 5 = 0కు సమాంతరం.
స్పర్శరేఖ సమీకరణము y = 2x + c
స్పర్శరేఖ నియమము c = \(\frac{a}{m}=\frac{4}{2}\) = 2
సమాంతర స్పర్శరేఖ సమీకరణము y = 2x + 2
2x + y + 2 = 0
స్పర్శ బిందువు \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=\left(\frac{4}{4} ; \frac{8}{2}\right)\) = (1, 4)
లంబంగా ఉండే స్పర్శరేఖ వాలు
m’ = –\(\frac{1}{m}\) = –\(\frac{1}{2}\)
లంబంగా ఉన్న స్పర్శరేఖ సమీకరణము y = m’x + c’
= (-\(\frac{1}{2}\)) x + c’
c’ = \(\frac{a}{m^{\prime}}=\frac{4}{\left(-\frac{1}{2}\right)}\) = – 8
లంబ స్పర్శరేఖ సమీకరణము
y = –\(\frac{1}{2}\) x – 8
2y = -x – 16
x + 2y + 16 = 0
స్పర్శ బిందువు \(\left(\frac{a}{m^{\prime^2}}, \frac{2 a}{m^{\prime}}\right)\)
= \(\left(\frac{4}{\left(\frac{1}{4}\right)}, \frac{8}{\left(-\frac{1}{2}\right)}\right)\)
= (16, -16).

ప్రశ్న 2.
y² = 4ax పరావలయానికి lx + my + n = 0 అభిలంబరేఖ అయితే al³ + 2alm² + nm² = 0 అని చూపండి.
సాధన:
పరావలయం సమీకరణము y² = 4ax
అభిలంబరేఖ సమీకరణము y + tx = 2at + at³
tx + y – (2at + at³) = 0 ………….. (1)
దత్తరేఖ సమీకరణము
lx + my + n = 0 ………. (2)
(1), (2) ఒకేరేఖను సూచిస్తున్నాయి.
గుణకాలను పోల్చగా

m³ తో గుణించగా
-nm² = 2al m² + al³
⇒ al³ + 2alm² + nm² = 0

ప్రశ్న 3.
వృత్తం x² + y² = 2a², పరావలయం y² = 8ax లకు ఉమ్మడి స్పర్శరేఖలు y = ± (x + 2a) అని చూపండి. [Mar. ’06]
సాధన:
పరావలయ స్పర్శరేఖ సమీకరణము y² = 8ax,
y = mx + \(\frac{2 a}{m}\)
m²x – my + 2a = 0 ……………… (1)
(1) రేఖ x² + y² = 2a², వృత్తాన్ని స్పృశిస్తుంది. (0, 0)
(1) కేంద్రం నుండి లంబదూరము a\(\sqrt{2}\) వ్యాసార్ధము.
\(\left|\frac{2 a}{\sqrt{m^2+m^4}}\right|\) = a\(\sqrt{2}\)
లేదా 4 = 2 (m⁴ + m²)
m⁴ + m² – 2 = 0
(m² + 2) (m² – 1) = 0 లేదా m = ± 1
కావలసిన స్పర్శరేఖలు
y = (1) x + \(\frac{2 a}{(1)}\) , y = (-1) x + \(\frac{2 a}{(-1)}\)
⇒ y = ± (x + 2a)

ప్రశ్న 4.
పరావలయం నాభి జ్యా అగ్రాల వద్ద గీసిన స్పర్శరేఖలు నియతరేఖ పై లంబంగా ఖండించుకొంటాయని చూపండి.
సాధన:

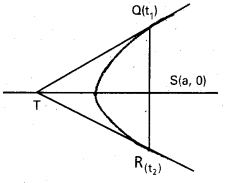
పరావలయ సమీకరణము y² = 4ax
Q(t₁) వద్ద స్పర్శరేఖా సమీకరణము.
t₁y = x + at₁²
R(t₂) వద్ద స్పర్శరేఖ సమీకరణము t₂y = x + at₂²
సాధించగా,
ఖండన బిందువు [at, t₂, a(t₁ + t₂)]
QR జ్యా సమీకరణము (t₁ + t₂) y = 2x + 2at₁t₂

ప్రశ్న 5.
x² = 4ay పరావలయానికి y = mx + c స్పర్శరేఖ కావడానికి నియమం కనుక్కోండి.
సాధన:
x² = 4ay కు స్పర్శరేఖ, స్పర్శరేఖ వాలు ‘m₁‘ పదాలలో
x = m₁ y + \(\frac{a}{m_1}\)
లేదా y = \(\frac{x}{m_1}-\frac{a}{m_1^2}\) …………… (i)
y = mx + c ………………… (ii)
(1) (2) పోల్చగా
m = \(\frac{1}{m_1}\) ; c = \(\frac{-a}{m_1^2}\)
m₁ = \(\frac{1}{m}\)
∴ c = \(\frac{-a}{(1 / m)^2}\)
c = – am² కావలసిన నియమము

ప్రశ్న 6.
y² = 8x పరావలయానికి (k, 0) నుంచి మూడు అభిలంబ రేఖలు గీశాం, అందులో ఒకటి అక్షరేఖ, మిగిలిన రెండు అభిలంబ రేఖలు ఒకదానికొకటి లంబంగా ఉంటే k విలువ కనుక్కోండి.
సాధన:
పరావలయంలో అభిలంబరేఖ సమీకరణము
y + xt = 2at + at³
ఈ అభిలంబరేఖ (k, 0) గుండా పోతుంది.
∴ kt = 2at + at
at³ + (2a – k) t = 0
at² + (2a – k) = 0
m₁ = 0, m₂ m₃ = -1 అని ఇవ్వబడింది.
(-t₂) (-t₃) = -1 t₂ t₃ = -1
\(\frac{2 a-k}{a}\) = – 1
2a – k = -a
k = 2a + a = 3a
పరావలయం సమీకరణము y² = 8x
4a = 8
⇒ a = 2
k = 3a = 3(2) = 6

ప్రశ్న 7.
y² = 4ax కు లంబ స్పర్శరేఖల ఖండన బిందువుల పథం నియతరేఖ x + a = 0 అని చూపండి.
సాధన:
పరావలయం యొక్క ఏదేని స్పర్శరేఖను
y = mx + \(\frac{a}{m}\) -గా తీసుకొనవచ్చును,
ఈ స్పర్శరేఖ P(x₁, y₁) గుండా పోతుంది.
my₁ = m²x₁ + a
m²x₁ – my₁ + a = 0.

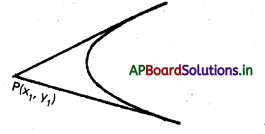
స్పర్శరేఖలు లంబంగా ఉన్నాయి.
⇒ m₁m₂ = -1
\(\frac{a}{x_1}\) = -1
x₁ = -a
నియతరేఖ x = -a, అనేది P(x₁, y₁) బిందుపథం

ప్రశ్న 8.
రెండు పరావలయాలు ఒకే శీర్షం, సమాన నాభి లంబం పొడవులు కలిగి ఉన్నాయి. వాటి అక్షాలు లంబంగా ఉన్నాయి. అప్పుడు వాటి ఉమ్మడి స్పర్శరేఖ, పరావలయ నాభి లంబాగ్రాల వద్ద స్పృశిస్తుందని చూపండి.
సాధన:

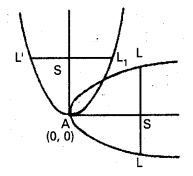
పరావలయాల సమీకరణాలు
y² = 4ax
x² = 4ay గా తీసుకుందాం.
x² = 4ay కు (2at, at²) వద్ద స్పర్శరేఖ
2atx = 2a(y + at²)
y = tx – at²
ఇది y² = 4ax కు స్పర్శరేఖ
∴ నియమము C = \(\frac{a}{m}\)
– at² = \(\frac{a}{t}\)
t³ = -1 ⇒ t = -1.
స్పర్శరేఖ సమీకరణం y = -x – a
x + y + a = 0.
L’ (a, – 2a) వద్ద స్పర్శరేఖ సమీకరణము
y (-2a) = 2a (x + a)
x + y + a = 0
∴ ఉమ్మడి స్పర్శరేఖ y² = 4ax పరావలయాన్ని
L (a, -2a) వద్ద స్పృశిస్తాయి.
L (-2a, a) వద్ద స్పర్శరేఖ సమీకరణము
x² = 4ay
x(-2a) = 2a (y + a)
x + y + a= 0
స్పర్శరేఖల ఉమ్మడి స్పర్శరేఖలు పరావలయాన్ని L’ (-2a, a) వద్ద స్పృశిస్తాయి.

ప్రశ్న 9.
y² = 4ax పరావలయ స్పర్శరేఖ పైకి నాభి నుంచి గీసిన లంబపాదాలు, శీర్షం వద్ద గీసిన స్పర్శరేఖపై ఉంటాయని చూపండి.
సాధన;
పరావలయం యొక్క ఏదేని స్పర్శరేఖ సమీకరణము
y = mx + \(\frac{a}{m}\)
Q(x₁, y₁) లంబపాదం
∴ y₁ = mx₁ + \(\frac{a}{m}\) …………….. (1)
SQ వాలు = \(\frac{y_1}{x_1-a}\)

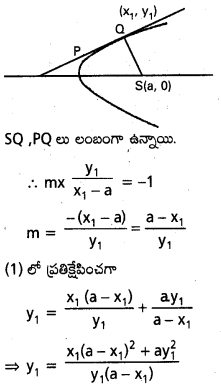
⇒ y₁² (a – x₁) = x₁ (a – x₁)² + ay₁²
⇒ ay₁² – x₁y₁² = x₁ (a² + x₁² – 2ax₁) + ay₁²
⇒ x₁ [x₁² – 2ax₁ + a² + y₁²] = 0
⇒ x₁ [(x₁ – a)² + y₁²] = 0
⇒ x₁ = 0
Q (x₁, y₁) బిందుపథం x = 0. i.e., ఇది పరావలయానికి శీర్షం వద్ద స్పర్శరేఖ.

ప్రశ్న 10.
పరావలయానికి నాభి జ్యా ఒక కొన వద్ద గీసిన స్పర్శరేఖ, రెండో కొన వద్ద గీసిన అభిలంబ రేఖకు సమాంతరంగా ఉంటుందని చూపండి.
సాధన:

P(t₁) వద్ద స్పర్శరేఖల సమీకరణాలు
t₁y = x + at₁²
P వద్ద స్పర్శరేఖ వాలు = \(\frac{1}{t_1}\) …………….. (2)
Q(t₂) వద్ద అభిలంబరేఖ సమీకరణము
y + xt₂ = 2at₂ + at₂³
Q వద్ద అభిలంబరేఖ వాలు = -t₂ ……………… (3)
(1), (2), (3) ల నుండి P వద్ద స్పర్శరేఖ వాలు = Q వద్ద అభిలంబరేఖ వాలు
P వద్ద స్పర్శరేఖ, Q వద్ద అభి లంబరేఖ సమాంతరము.

III.

ప్రశ్న 1.
y² = 4ax పరావలయానికి t₁ వద్ద గీసిన అభిలంబరేఖ పరావలయాన్ని తిరిగి t₂ వద్ద ఖండిస్తే t₁t₂ + t₁² + 2 = 0 అని చూపండి. [May ’07]
సాధన:
అభిలంబ రేఖ సమీకరణము
y – y₁ = \(\frac{-y_1}{2 a}\) (x – x₁)
y – 2at₁ = \(\frac{-2 \mathrm{at}_1}{2 \mathrm{a}}\) (x – at₁²)
(1) రేఖ పరావలయాన్ని తిరిగి (at₂², 2at₂) వద్ద ఖండిస్తుంది.
∴ 2at₂ – 2at₁ = t₁ (at₂² – at₁²)
–\(\frac{2}{t_1}\) = t₁ + t₂ ⇒ -2 = t₁² + t₁t₂
⇒ t₁² + t₁t₂ + 2 = 0

ప్రశ్న 2.
y² = 4ax పరావలయానికి బాహ్య బిందువు P నుంచి గీసిన స్పర్శరేఖలు అక్షరేఖతో θ₁, θ₂ కోణాలు చేస్తున్నాయి. cot θ₁ + cot θ₂ విలువ స్థిర సంఖ్య ‘d’ అయితే, అలాంటి P లు క్షితిజ సమాంతర రేఖపై ఉంటాయని చూపండి.
సాధన:
పరావలయం యొక్క స్పర్శరేఖ సమీకరణము
y = mx + \(\frac{a}{m}\)
ఈ స్పర్శరేఖ P(x₁, y₁) గుండా పోతుంది.
y₁ = mx₁ + \(\frac{a}{m}\)
my₁ = m²x₁ + a = 0
m²x₁ – my₁ + a = 0
ఈ సమీకరణం మూలాలు m₁, m₂, అయితే
m₁ + m₂ = \(\frac{y_1}{x_1}\), m₁m₂ = \(\frac{a}{x_1}\)
cot θ₁ + cot θ₂ = a అని ఇవ్వబడింది.

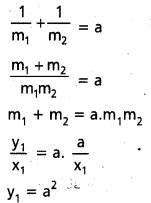
P(x₁, y₁) బిందుపథం y = a² ఇది క్షితిజ రేఖ.

ప్రశ్న 3.
2x² + 2y² = a² వృత్తం, y² = 4ax పరావలయానికి ఉమ్మడి స్పర్శరేఖలు y² = – 4ax యొక్క నాభి వద్ద ఖండించుకొంటాయని చూపండి.
సాధన:
దత్త వృత్తము 2x² + 2y² = a²
కేంద్రం = (0, 0); వ్యాసార్ధము = \(\frac{a}{\sqrt{2}}\)
దత్త పరావలయము y² = 4ax
y = mx + \(\frac{a}{m}\) స్పర్శరేఖ అనుకుందాం.
2x² + 2y² = a² స్పృశిస్తుంది.
⇒ (0, 0) నుండి లంబదూరము = వ్యాసార్థము
⇒ \(\left|\frac{\frac{a}{m}}{\sqrt{m^2+1}}\right|=\frac{a}{\sqrt{2}}\)
⇒ \(\frac{\frac{a^2}{m^2}}{m^2+1}=\frac{a^2}{2}\)
⇒ \(\frac{2 a^2}{m^2}\) = a² (m² + 1)
⇒ 2 = m⁴ + m²
⇒m ⇒ m⁴ + m² – 2 = 0
⇒ (m² – 1) (m² + 2) = 0 (∵ m² + 2 ≠ 0)
m² – 1 = 0 ⇒ m = ± 1
y² = – 4ax పరావలయం యొక్క నాభి వద్ద ఖండిస్తుంది.

ప్రశ్న 4.
y² = 4ax పరావలయంపై రెండు బిందువుల y నిరూపకాల మొత్తం, అదే పరావలయంపై వేరొక రెండు బిందువుల y నిరూపకాల మొత్తానికి సమానం అయితే, మొదటి రెండు బిందువులను కలిపే జ్యా, మిగిలిన రెండు బిందువులను కలిపే జ్యాకు సమాంతరంగా ఉంటుందని చూపండి.
సాధన:

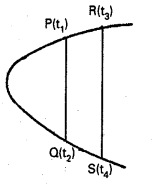
పరావలయ సమీకరణము y² = 4ax
P(t) మరియు Q(t) లను కలిపే జ్యా సమీకరణము
(t₁ + t₂) y = 2x + 2 at₁ t₂
PQ వాలు = \(\frac{2}{t_1+t_2}\) ……………… (1)
R(t₃) మరియు S(t₄) లు కలిపే జ్యా సమీకరణము
(t₃ + t₄) y = 2x + 2at₃t₄
RS వాలు = \(\frac{2}{t_3+t_4}\) ………………. (2)
దత్తాంశం ప్రకారం 2at₁ + 2at₂ = 2at₃ + 2at₄
i.e., 2a (t₁ + t₂) = 2a (t₃ + t₄)
t₁ + t₂ = t₃ + t₄ …………….. (3)
(1), (2), (3) ల నుండి PQ వాలు = RS వాలు
i.e., PQ, RS లు సమాంతరాలు.

ప్రశ్న 5.
y² = 4ax పరావలయంపై బిందువు ‘t’ వద్ద అభిలంబ జ్యా, శీర్షం వద్ద లంబకోణం చేస్తే t = ± \(\sqrt{2}\) అని చూపండి.
సాధన:
పరావలయం సమీకరణము y² = 4ax …………… (1)
‘t’ వద్ద లంబరేఖ సమీకరణాలు
tx + y = 2at + at³

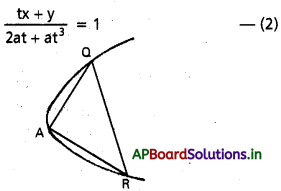
(2) సహాయంతో (1) ని సమఘాతపరిస్తే AQ, ARల ఉమ్మడి సమీకరణాలు
y² = \(\frac{4 a x \cdot(t x+y)}{a\left(2 t+t^3\right)}\)
y² (2t + t³) = 4tx² + 4xy
4tx² + 4xy – (2t + t³) y² = 0
AQ, AR లు లంబంగా ఉన్నాయి.
x² గుణకం + y² గుణకం = 0
4t – 2t – t³ = 0
2t – t³ = 0
-t(t² – 2) = 0
t² – 2 = 0 ⇒ t² = 2
t = ± \(\sqrt{2}\)