AP Inter 2nd Year Physics Notes Chapter 8 అయస్కాంతత్వం-ద్రవ్యం

Students can go through AP Inter 2nd Year Physics Notes 8th Lesson అయస్కాంతత్వం-ద్రవ్యం will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 8th Lesson అయస్కాంతత్వం-ద్రవ్యం

→ సూదంటు రాయి ఒక సహజ అయస్కాంతం. ఇది మాగ్నటైట్ అనే ఇనుప ఖనిజము. సూదంటు రాయి అనగా దారి చూపించునది.

→ అయస్కాంతం యొక్క అయస్కాంత క్షేత్ర రేఖలు అవిచ్ఛిన్న సంవృత ఉచ్చులను ఏర్పరుచును.

→ విద్యుత్ ప్రవాహ ఉచ్చుతో ముడిపడి ఉన్న అయస్కాంత ద్విధ్రువ భ్రామకము m = NIA. ఇక్కడ ఉచ్చులో చుట్ల సంఖ్య N. I విద్యుత్ ప్రవాహము మరియు A సదిశ వైశాల్యం.

→ సాలినాయిడ్ అయస్కాంత భ్రామకం పరిమాణం m = n(2l) I (πa²)

→ ఒక దండాయస్కాంత అక్షీయ అయస్కాంత క్షేత్రము B_A = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^3}\)

→ ఏకరీతి అయస్కాంత క్షేత్రంలో ద్విధ్రువం (సూది) పై టార్క్ τ = m × B

→ ఒక దండాయస్కాంతం మధ్య లంబక్షేత్రము B_E = \(\frac{\mu_0}{4 \pi}\)

→ అయస్కాంతత్వంలో గాస్ నియమము : ఏదైనా సంవృత తలం ద్వారా నికర, అయస్కాంత అభివాహము సున్న, i.e. ∫_sB.ds = 0

→ అయస్కాంత ఉత్తర మరియు దక్షిణ దృవములను కలుపు ఊహారేఖ ద్వారా పోవు లంబతలంను, ఆ ప్రదేశంలో అయస్కాంత యామ్యోత్తర రేఖ అంటారు.

→ నిజ భౌగోళిక ఉత్తర ధృవము మరియు కంపాసు సూచి చూపు ఉత్తర ధృవమునకు మధ్య గల కోణంను దిక్పాతము అంటారు.

→ భూమి అయస్కాంత మొత్తం తీవ్రత తెలుపు దిశకు మరియు అయస్కాంత యామ్యోత్తర రేఖకు మధ్య కోణంను అవపాతము అంటారు..

→ ప్రమాణ ఘనపరిమాణంలో అయస్కాంత భ్రామకంను అయస్కాంతీకరణం అంటారు.

దీని ప్రమాణము Am^-1 మరియు దీని మితులు L^-1A.

→ 300K వద్ద, రుణ డయా అయస్కాంత పదార్థాలు బిస్మత్, రాగి, వజ్రము, బంగారము, సీసము, పాదరసము, నైట్రోజన్ (S.T.P), వెండి, సిలికాన్,

→ 300K వద్ద, ధన పారా అయస్కాంత పదార్థాలు అల్యూమినియం, కాల్షియం, క్రోమియం, లిథియం, మెగ్నీషియం, నియోబియమ్, ఆక్సిజన్ (STP), ప్లాటినమ్, టంగస్టన్.

→ డయా అయస్కాంత పదార్థాలకు, -1 ≤ χ < 0; 0 ≤ μ_r < 1; μ < μ₀.

→ పారా అయస్కాంత పదార్థాలకు, 0 < χ < ε, 1 < μ_r < 1 + ε; μ > μ₀.

→ ఫెర్రో అయస్కాంత పదార్థాలకు, χ >> 1; μ_r >> 1; μ < μ₀.

→ పారా అయస్కాంత అయస్కాంతీకరణము, పరమ ఉష్ణోగ్రత T.కు విలోమానుపాతంలో ఉండును.
M = \(\frac{\mu_0}{T}\) లేకు తుల్యంగా, χ = C\(\frac{\mu_0}{T}\)

→ పారా అయస్కాంత నమూనాపై, క్షేత్రం పెంచినా లేక ఉష్ణోగ్రత తగ్గించినా, అయస్కాంతీకరణ సంతృప్త విలువ Ms, చేరు వరకు పెరుగును. ఈ స్థితిలో ధృవాలన్నీ క్షేత్ర దిశలో పూర్తిగా అమరును.

→ ఫెర్రో అయస్కాంత పదార్థ సూక్ష్మ ఘనపరిమాణం (10^-6 cm³ నుండి 10^-2 cm³) ను డొమైన్ అంటారు.

→ డొమైన్ పరిమాణము 1mm మరియు డొమైన్లో పరమాణువుల సంఖ్య 10¹¹.

→ కొన్ని ఫెర్రో అయస్కాంత పదార్థాలలో అయస్కాంతీకరణ దృఢంగా ఉంటుంది. అటువంటి పదార్థాలను కఠిన అయస్కాంత పదార్థాలు లేక కఠిన ఫెర్రో అయస్కాంత పదార్థాలంటారు. ఫెర్రో అయస్కాంత పదార్థాలకు, μ_r > 1000.

→ ఫెర్రో అయస్కాంత పదార్థం, పారా అయస్కాంత పదార్థంగా మారు ఉష్ణోగ్రతను, క్యూరీ ఉష్ణోగ్రత T అంటారు.

→ I మరియు B లు H వెనక ఉండటాన్ని, శైథిల్యం అంటారు.

→ H = 0 వద్ద I విలువను రెటింటివిటి అంటారు.

→ H యొక్క తిరోదిశలో I ను సున్నాకు చేర్చుటకు కావాల్సిన అయస్కాంత బల విలువను కొయిర్సివిటి అంటారు.

→ విద్యుదయస్కాంతాలు, విద్యుత్ గంటలు, లౌడ్ స్పీకర్స్ మరియు టెలిఫోన్ డయఫ్రమ్స్ వాడతారు.

→ కూలుమ్ నియమము, F = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}^2}\) = 10^-7 × \(\frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}^2}\)

→ అయస్కాంత ద్విధ్రువం, \(\overrightarrow{\mathbf{M}}=\mathrm{m}(\overrightarrow{2 l})\)

→ విద్యుత్ లూపు అయస్కాంత భ్రామకము, \(\vec{M}=I \vec{A}\)

→ కక్ష్యా చలనం వల్ల అయస్కాంత భ్రామకము, μ_l = n\(\left(\frac{\mathrm{eh}}{4 \pi \mathrm{m}_{\mathrm{e}}}\right)\)

→ బోర్ మాగ్నిటాన్, μ_B = \(\frac{\mathrm{eh}}{4 \pi \mathrm{m}_{\mathrm{e}}}\)

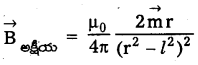
→ పొట్టి ద్విధ్రువంకు,

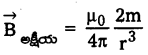
→ \(\overrightarrow{\mathrm{B}_{\mathrm{e}}}=\frac{\mu_0}{4 \pi}=\frac{\overrightarrow{\mathrm{m}}}{\left(\mathrm{r}^2+l^2\right)^{3 / 2}}\) పొట్టి దండాయస్కాంతమునకు, B_e = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{m}}{\mathrm{r}^3}\)

→ ఏదైనా బిందువు వద్ద పొట్టి అయస్కాంత ద్విధ్రువం వల్ల అయస్కాంత క్షేత్రము B = \(\frac{\mu_0}{4 \pi} \frac{M \sqrt{3 \cos ^2 \theta+1}}{\mathbf{r}^3}\)

→ టార్క్ \(\vec{\tau}=\overrightarrow{\mathrm{m}} \times \overrightarrow{\mathrm{B}}\)

→ అయస్కాంత క్షేత్రంలో ఒక దండాయస్కాంతమును ఉంచినపుడు స్థితిజ శక్తి U = -m B cos θ = –\(\overrightarrow{\mathrm{m}} \times \overrightarrow{\mathrm{B}}\)

→ అయస్కాంతత్వంలో గాస్ నియమము \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{ds}}\)

→ అయస్కాంత తీవ్రత H = \(\frac{B_0}{\mu_0}\)

→ అయస్కాంతీకరణ తీవ్రత I = \(\frac{\mathrm{M}}{\mathrm{V}}=\frac{\mathrm{m} \times 2 l}{\mathrm{~A} \times 2 l}=\frac{\mathrm{m}}{\mathrm{A}}\)

→ అయస్కాంత అభివాహం Φ = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\Delta \mathrm{s}}\)

→ అయస్కాంత ససెప్టిబిల్టి χ_m = \(\frac{I}{H}\)

→ అయస్కాంత పర్మియబిల్టి μ = \(\frac{\mathrm{B}}{\mathrm{H}}\)

→ μ = μ₀ (1 + χ_m) మరియు μ_r = 1 + χ_m

→ క్యూరీ నియమము χ_m α \(\frac{1}{T}\) ⇒ χ_m = T స్థిరాంకం.