AP Inter 2nd Year Maths 2B Solutions Chapter 5 అతిపరావలయం Ex 5(a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 5 అతిపరావలయం Exercise 5(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 5 అతిపరావలయం Exercise 5(a)

అభ్యాసం – 5(ఎ)

I.

ప్రశ్న 1.
ఉత్కేంద్రత \(\frac{3}{2}\), ఒక నాభి (1, -3), అనురూప నియతరేఖ y = 2 గా గల అతిపరావలయ సమీకరణం కనుక్కోండి.
సాధన:
నాభి, 5(1, -3) నియతరేఖ సమీకరణం y – 2 – 0

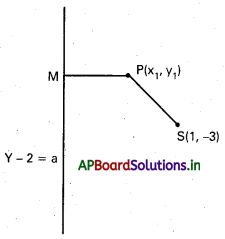
P(x₁, y₁) అతి పరావలయం మీది ఏదేని బిందువు SP కలుపు నియతరేఖ మీదకు PM అనే లంబాన్ని గీయండి.
S.P.= e. PM ⇒ SP² = e². PM²
(x₁ – 1)² + (y₁ + 3)² = \(\frac{9}{4}\left|\frac{\left(y_1-2\right)}{\sqrt{1+0}}\right|^2\)
x₁² + 1 – 2x₁ + y₁² + 9 + 6y₁ = \(\frac{9}{4}\) (y₁ – 2)²
4x₁² + 4y₁² – 8x₁ + 24y₁ + 40 = (y₁² + 4 – 4y₁) – 9y₁² – 36y₁ +36
4x₁² – 5y₁² – 8x₁ + 60y₁ + 4 = 0
P(x₁, y₁) యొక్క బిందుపథము
4x² – 5y² – 8x + 60y + 4 = 0
ఇది కావలసిన అతిపరావలయ సమీకరణము.

ప్రశ్న 2.
3x – 4y = 12, 3x + 4y = 12 సరళరేఖలు అతి పరావలయం S = 0 పై ఖండించుకొంటే, S = 0 ఉత్కేంద్రత కనుక్కోండి.
సాధన:
దత్త రేఖలు 3x – 4y = 12
3x + 4y = 12
ఖండన బిందువు P(4, 0)
P అతిపరావలయం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 మీద బిందువు
\(\frac{16}{a^2}\) = 1
a² = 16.
ఉత్కేంద్రత కనుగొనడానికి దత్తాంశం సరిపోదు.

ప్రశ్న 3.
నాభులు (±5, 0), తిర్యక్ అక్షం పొడవు 8గా గల అతిపరావలయ సమీకరణం కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
నాభులు S (±5, 0) ∴ ae = 5
తిర్యగాక్షము పొడవు = 2a = 8 a = 4
e = \(\frac{5}{4}\)
b² = a² (e² – 1) = 16 \(\left(\frac{25}{16}-1\right)\) = 9
అతిపరావలయ సమీకరణము \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
9x² – 16y² = 144

ప్రశ్న 4.
(1,–1) బిందువు గుండా పోతూ x + 2y + 3 = 0, 3x + 4y + 5 = 0 లు అనంత స్పర్శరేఖలుగా గల అతిపరావలయ సమీకరణం కనుక్కోండి.
సాధన:
అనంత స్పర్శరేఖల ఉమ్మడి సమీకరణము
(x + 2y + 3) (3x + 4y + 5) = 0
∴ అతిపరావలయ సమీకరణము
(x + 2y + 3) (3x + 4y + 5) + k = 0 గా తీసుకొనవలెను.
అతిపరావలయం P(1, 1) గుండా పోతుంది.
(1 – 2 + 3) (3 – 4 + 5) + k = 0
8 + k = 0 ⇒ k = -8
అతిపరావలయ సమీకరణము
(x + 2y + 3) (3x + 4y + 5) – 8 = 0
3x² + 6xy + 9x + 4xy + 8y² + 12y + 5x + 10y + 15 – 8 = 0
3x² + 10xy + 8y² + 14x + 22y + 7 = 0

ప్రశ్న 5.
x² – 4y² = 5 అతిపరావలయానికి 3x – 4y + k = 0 స్పర్శరేఖ అయితే k విలువ కనుక్కోండి. [T.S. Mar. ’17]
సాధన:
అతిపరావలయ సమీకరణం x² – 4y² = 5
\(\frac{x^2}{5}-\frac{y^2}{\left(\frac{5}{4}\right)}\) = 1
a² = 5, b² = \(\frac{5}{4}\)
దత్తరేఖ సమీకరణము 3x – 4y + k = 0
4y = 3x + k
у = \(\frac{3}{4}\)x + \(\frac{k}{4}\)
m = \(\frac{3}{4}\) ; c = \(\frac{k}{4}\)
స్పర్శరేఖ నియమము c² = a²m² – b²
\(\frac{k^2}{16}\) = 5. \(\frac{9}{16}\) – \(\frac{5}{4}\)
k² = 45 – 20 = 25
k = ± 5

ప్రశ్న 6.
\(\frac{x^2}{16}-\frac{y^2}{9}\) = 1 పై ఏ బిందువునుంచైనా అనంత స్పర్శ రేఖలకు గల లంబదూరాల లబ్దం కనుక్కోండి.
సాధన:
అతిపరావలయ సమీకరణము \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
a² = 16, b³ = 9
అనంత స్పర్శరేఖల మీద అతిపరావలయం మీది ఏదేని బిందువు నుండి లంబదూరాల లబ్దము
= \(\frac{a^2 b^2}{a^2+b^2}=\frac{16 \times 9}{16+9}=\frac{144}{25}\)

ప్రశ్న 7.
ఒక అతిపరావలయ ఉత్కేంద్రత \(\frac{5}{4}\) అయితే దాని సంయుగ్య అతిపరావలయ ఉత్యేంద్రత కనుక్కోండి. [A.P. Mar. ’17 A.P. Mar. ’16 (Mar, ’13)]
సాధన:
అతిపరావలయ, సంయుగ్మ అతిపరావలయాల ఉత్కేంద్రతలు
e, e₁ అయితే \(\frac{1}{\mathrm{e}^2}+\frac{1}{\mathrm{e}_1^2}\) = 1
e = \(\frac{5}{4}\) అని ఇవ్వబడింది.
= \(\frac{16}{25}+\frac{1}{e_1^2}\) = 1
\(\frac{1}{\mathrm{e}_1^2}\) = 1 – \(\frac{16}{25}\) = \(\frac{9}{25}\)
e₁² = \(\frac{25}{9}\) ⇒ e₁ = \(\frac{5}{3}\)

ప్రశ్న 8.
3x = ± 5yలు అనంత స్పర్శరేఖలుగా కలిగి, శీర్షాలు (±5, 0) గా గల అతిపరావలయ సమీకరణం కనుక్కోండి.
సాధన:
అనంత స్పర్శరేఖల సమీకరణం 3x = ± 5y
3x – 5y = 0, 3x + 5y = 0
అనంత స్పర్శరేఖల ఉమ్మడి సమీకరణం
(3x – 5y) (3x + 5y) = 0
9x² – 25y² = 0
అతిపరావలయ సమీకరణం 9x² – 25y² = k
అతిపరావలయం శీర్షం (5, 0) గుండా పోతుంది.
9(5)² – 0 = k ⇒ k = 225
అతిపరావలయ సమీకరణం 9x² – 25y² = 225

ప్రశ్న 9.
3x² – 4y² = 12 అతిపరావలయానికి θ = \(\frac{\pi}{3 }\) వద్ద అభిలంబ రేఖా సమీకరణం కనుక్కోండి.
సాధన:
అతిపరావలయ సమీకరణం
3x² – 4y² = 12

ప్రశ్న 10.
అనంత స్పర్శరేఖల మధ్యకోణం 30° గా గల అతి పరావలయ ఉత్యేంద్రత కనుక్కోండి.
సాధన:
అనంత స్పర్శరేఖల మధ్య కోణము
= 2θ = 30°
θ = 15°
tan θ = tan 15° = \(\frac{b}{a}\)
e² = \(\frac{a^2+b^2}{a^2}\) = 1 + tan² 15°

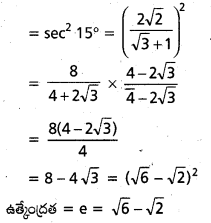
II.

ప్రశ్న 1.
కింది అతిపరావలయాలకు ఉత్కేంద్రత, నాభులు, నియత రేఖా సమీకరణాలు, కేంద్రం, నాభి లంబం పొడవు కనుక్కోండి.
i) 16y² – 9x² = 144
సాధన:
అతిపరావలయం సమీకరణం
16y² – 9x² = 144
\(\frac{y^2}{9}-\frac{x^2}{16}\) = 1
a² = 16, b² = 9
కేంద్రం C(0, 0)
b²e² = a² + b² = 16 + 9
= 25 ⇒ be = 5
నాభులు 5(0, ± ae) = (0, ± 5)
ఉత్యేంద్రత \(\frac{b e}{b}=\frac{5}{3}\)
నియతరేఖల సమీకరణాలు y = ± b/e
= ±3 . \(\frac{5}{3}\)
5y = ± 9
నాభిలంబం పొడవు = 2 . \(\frac{a^2}{b}\)
= 2 . \(\frac{16}{3}\) = \(\frac{32}{3}\)

ii) x² – 4y² = 4 [A.P. Mar. ’16 (May ’11)]
సాధన:
అతిపరావలయ సమీకరణం \(\frac{x^2}{4}-\frac{y^2}{1}\) = 1
a² = 4, b² = 1
కేంద్రం c(0, 0)
a²e² = a² + b² = 4 + 1 = 5
ae = \(\sqrt{5}\)
నాభులు (±ae, 0) = (±\(\sqrt{5}\), 0)
ఉత్కేంద్రత = \(\frac{a e}{a}=\frac{\sqrt{5}}{2}\)
నియతరేఖల సమీకరణాలు x = ±\(\frac{a}{e}\) = ± 2 . \(\frac{a}{e}\)
⇒ \(\sqrt{5}\)x = ±4
⇒ \(\sqrt{5}\)x ± 4 = 0
నాభిలంబ పొడవు = \(\frac{2 b^2}{a}=\frac{2.1}{2}\) = 1

iii) 5x² – 4y² + 20x + 8y = 4
సాధన:
5(x² + 4x + 4) – 4 (y² – 2y + 1) = 4 + 20 – 4
5(x + 2)² – 4(y – 1)² = 20
\(\frac{(x+2)^2}{4}-\frac{(y-1)^2}{5}\) = 1
a² = 4, b² = 5 ⇒ a < b
కేంద్రం C(-2, +1)
a²e² = a² + b² = 4 + 5 = 9
ae = 3
ఉత్కేంద్రత = \(\frac{a \mathrm{e}}{\mathrm{a}}=\frac{3}{2}\)
నాభులు (h ± ae, k) = (-2 ± 3, 1)
= (−5, 1) మరియు (1, 1)
నియతరేఖల సమీకరణము x – h = ± \(\frac{a \mathrm{e}}{\mathrm{a}}\)
x + 2 = ± 2 . \(\frac{2}{3}\)
3x + 6 = ±4
3x + 10 = 0 (లేదా) 3x + 2 = 0
నాభిలంబం పొడవు = \(\frac{2 b^2}{a}=\frac{2.5}{2}\) = 5

iv) 9x² – 16y² + 72x – 32y – 16 = 0
సాధన:
అతిపరావలయం సమీకరణము
9x² – 16y² + 72x – 32y – 16 = 0
⇒ 9(x² + 8x) – 16(y² + 2y) = 16
⇒ 9(x² + 8x + 16) – 16 (y² + 2y + 1) = 16 + 144 – 16
⇒ 9(x + 4)² – 16(y + 1)² = 144.
⇒ \(\frac{(x+4)^2}{16}-\frac{(y+1)^2}{9}\) = 1
\(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}\) = 1 తో పోల్చగా
a² = 16, b² = 9, h = -4, k = -1
కేంద్రం (h, k) = (-4, -1)
e = \(\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{16+9}{16}}\)
= \(\sqrt{\frac{25}{16}}=\frac{5}{4}\)
నాభులు = (h ± ae, k) = (-4 ± 4 . \(\frac{5}{4}\), 1)
= (-4 ± 5, -1)
= (1, -1), (-9, -1)
నియతరేఖల సమీకరణాలు
x + 4 = ± 4 . \(\frac{4}{5}\)
= ± \(\frac{16}{5}\)
5x + 20 = ±16
నియతరేఖల సమీకరణాలు 5x + 4 = 0
5x + 36 = 0
నాభి లంబము పొడవు = \(\frac{2 b^2}{a}\)
= \(\frac{2 \times 9}{4}=\frac{9}{2}\)

ప్రశ్న 2.
ఉత్కేంద్రత 2, నాభులు (4,2), (8, 2) గా గల అతిపరా వలయం సమీకరణం కనుక్కోండి.
సాధన:
నాభులు (4, 2), (8, 2),
కేంద్రం C నాభుల మధ్య బిందువు
∴ కేంద్రం \(\left(\frac{4+8}{2}, \frac{2+2}{2}\right)\) = (6, 2)
ae = 6 – 4 = 2
e = 2 ⇒ a = \(\frac{\mathrm{ae}}{\mathrm{e}}=\frac{2}{2}\) = 1
b² = a² (e² – 1) = 1(4 – 1) = 3
అతిపరావలయ సమీకరణం
\(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}\) = 1
\(\frac{(x-6)^2}{1}-\frac{(y-2)^2}{3}\) = 1
3 తో గుణించగా,
3(x – 6)² – (y – 2)² = 3
⇒ 3(x² – 12x + 36) – (y² – 4y + 4) = 3
⇒ 3x² – 36x + 108 – y² + 4y – 4 – 3 = 0
3x² – y² – 36x + 4y + 101 = 0

ప్రశ్న 3.
తిర్యక్ అక్షం పొడవు 6గా కలిగి కేంద్రం, నాభులను కలిపే రేఖాఖండానికి శీర్షం మధ్యబిందువుగా గల అతిపరావలయ సమీకరణం కనుక్కోండి.
సాధన:
CA – AS అని ఇవ్వబడింది.

a = ae – a
2a = ae ⇒ e = 2
తిర్యక్ అక్షం పొడవు = 2a = 6 ⇒ a = 3
b² = a²(e² – 1) = 9(4 – 1) = 27
అతిపరావలయ సమీకరణం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
\(\frac{x^2}{9}-\frac{y^2}{27}\) = 1
3x² – y² = 27

ప్రశ్న 4.
x + 2y = 0 కు (i) సమాంతరంగా (ii) లంబంగా ఉంటూ అతిపరావలయం x² – 4y² = 4 ను స్పృశించే రేఖల సమీకరణాలు కనుక్కోండి. [May ’06]
సాధన:
అతిపరావలయ సమీకరణం x² – 4y² = 4
\(\frac{x^2}{4}-\frac{y^2}{1}\) = 1
a² = 4, b² = 1
i) స్పర్శరేఖ x + 2y = 0 కు సమాంతరంగా ఉంటుంది.
m = –\(\frac{1}{2}\)
c² = a²m² – b²
= 4 . \(\frac{1}{4}\) – 1 = 1 – 1 = 0
c = 0
సమాంతర స్పర్శరేఖ సమీకరణం
y = mx + c
= –\(\frac{1}{2}\)x
2y = -x
x + 2y = 0
దీనికి సమాంతర స్పర్శరేఖలు లేవు

ii) స్పర్శరేఖ x + 2y = 0 కు లంబంగా ఉంటే
స్పర్శరేఖ వాలు = m = \(\frac{-1}{\left(-\frac{1}{2}\right)}\) = 2
c² = a²m² – b² = 4. 4 – 1 = 15
c = ± \(\sqrt{15}\)
లంబ స్పర్శరేఖ సమీకరణము y = 2x ± \(\sqrt{15}\)

ప్రశ్న 5.
2x² – 3y² = 6 అతిపరావలయానికి (-2, 1) గుండా పోయే స్పర్శరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
అతిపరావలయ సమీకరణం 2x² – 3y² = 6
\(\frac{x^2}{3}-\frac{y^2}{2}\) = 1
‘స్పర్శరేఖ వాలు ‘m’ అనుకొనుము.
స్పర్శరేఖ P(-2, 1) గుండా పోతుంది
స్పర్శరేఖ సమీకరణము
y – 1 = m(x + 2) = mx + 2m
y = mx + (2m + 1) …………………….. (1)
స్పర్శరేఖ నియమం c² = a²m² – b²
(2m + 1)² = 3m² – 2
4m² + 4m + 1 = 3m² – 2
m² + 4m + 3 = 0
(m + 1) (m + 3) = 0
m = -1 (లేదా) – 3

సందర్భం: (i) : m = -1
(1) లో ప్రతిక్షేపిస్తే స్పర్శరేఖ సమీకరణం
y = -x – 1
x + y + 1 = 0
సందర్భం : (ii) : m = – 3
స్పర్శరేఖ సమీకరణం y = – 3x – 5
3x + y + 5 = 0

ప్రశ్న 6.
అతిపరావలయంపై ఏదైనా బిందువు నుంచి దాని అనంత స్పర్శరేఖలకు గల లంబదూరాల లబ్దం స్థిరం అని చూపండి.
సాధన:
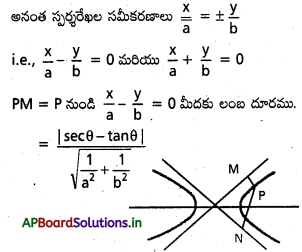
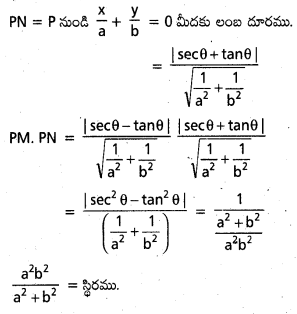
అభిలంబరేఖ సమీకరణం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
అతి పరావలయం పైగలఏదైనా బిందువు
P(a sec θ, b tan θ)

III.

ప్రశ్న 1.
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 అతిపరావలయం స్పర్శరేఖలు, అతిపరా వలయం తిర్యక్ అక్షంతో θ₁, θ₂ కోణాలు చేస్తున్నాయి. tan θ₁ + tan θ₂ = k అయితే ఆ స్పర్శరేఖల ఖండన బిందువు 2xy = k(x² – a²) వక్రంపై ఉంటుందని చూపుము.
సాధన:
అతిపరావలయ సమీకరణం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
అతిపరావలయానికి స్పర్శరేఖను
y = mx ± \(\sqrt{a^2 m^2-b^2}\) గా తీసుకొనవచ్చు.
స్పర్శరేఖల ఖండనబిందువు P(x₁, y₁) అయితే
y₁ = mx₁ ±\(\sqrt{a^2 m^2-b^2}\)
y₁ – mx₁ = ±\(\sqrt{a^2 m^2-b^2}\)
ఇరువైపులా వర్గీకరించగా
(y₁ – mx₁)² = a²m² – b².
y₁² + m²x₁² – 2m x₁y₁ – a²m² + b²
m² (x₁² – a²) – 2mx₁y₁ + (y₁² + b²) = 0
ఇది m లో వర్గ సమీకరణము.
m₁, m₂ లు మూలాలు అనుకుందాం.
m₁ + m₂ = \(\frac{2 x_1 y_1}{x_1^2-a^2}\)
tan θ₁ + tan θ₂ = \(\frac{2 x_1 y_1}{x_1^2-a^2}\)
i.e., k = \(\frac{2 x_1 y_1}{x_1^2-a^2}\) (లేదా)
2x₁y₁ = k(x₁² – a²)
బిందువు P(x₁, y₁) 2xy = k(x² – a²) వక్రము మీద ఉంటుంది.

ప్రశ్న 2.
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 యొక్క ఏదైనా స్పర్శరేఖపై నాభుల లంబపాదాలు అనుబంద (సహాయక) వృత్తంపై ఉంటాయని చూపండి.
సాధన:
అతిపరావలయ సమీకరణం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1

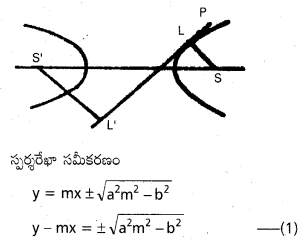
(±ae, 0) నుండి స్పర్శరేఖ మీదికి గీయబడిన
లంబం సమీకరణము
У = –\(\frac{1}{m}\) (x ± ae)
x + my = ±ae ……………… (2)
(1), (2) లను వర్గీకరించి కూడగా,
(y – mx)² + (x + my)² = a²m² – b² + a²e²
⇒ y² + m²x² – 2mxy + x² + m²y² + 2mxy = a²m² – a²(e² – 1) + a²e²
⇒ (x² + y²) (1 + m²) = a²m² – a²e² + a² + a²e²
= a² (1 + m²)
x² + y² = a² ఇది సహాయక వృత్తము.
నాభుల నుండి స్పర్శరేఖ మీదకు గీయబడిన లంబపాదాలు సహాయక వృత్తం మీద ఉంటాయి.

ప్రశ్న 3.
\(\frac{x^2}{9-c}+\frac{y^2}{5-c}\) = 1 సమీకరణం
i) c < 5 అయితే దీర్ఘవృత్తం (‘c’ ఏదైనా వాస్తవ స్థిరాంకం)
ii) 5 < C < 9 అయితే అతిపరావలయం (‘c’ ఏదైనా వాస్తవ స్థిరాంకం) iii) (i) లో గల ప్రతి దీర్ఘవృత్తం (ii) లో ప్రతి అతిపరా వలయం నాభులు (±2, 0) ‘c’ పై ఆధారపడవని చూపండి. సాధన: i) దత్త సమీకరణం \(\frac{x^2}{9-c}+\frac{y^2}{5-c}\) = 1 ఈ సమీకరణం దీర్ఘవృత్తాన్ని 9 – c > 0 గా సూచిస్తే
5 – c > 0
∴ c < 9, c < 5
⇒ c < 5

ii) దత్త సమీకరణం \(\frac{x^2}{9-c}+\frac{y^2}{5-c}\) = 1
ఈ సమీకరణం అతిపరావలయాన్ని సూచిస్తే
9 – c > 0 మరియు 5 – c < 0
9 > c, 5 < c i.e., 5 < c < 9

iii) రెండు సందర్భాలలోను
సందర్భం (i) : a² = 9 – c, b² = 5 – c
a² – b² = ( 9 – c) – (5 – c)
= 9 – c – 5 + c = 4
a²e² = 4 ⇒ ae = 2
నాభులు (± ae, 0) = (±2,0)
సందర్భం (ii) : a² = 9 – c, b² = c – 5
a² + b² = 9 – c + c – 5 = 4
a²e² = 4 ⇒ ae = 2
నాభులు (±ae, 0) = (±2, 0)

ప్రశ్న 4.
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 అతిపరావలయ అనంత స్పర్శరేఖల మధ్యకోణము 2 tan^-1 \(\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\) లేదా 2 sec^-1 (e) అని చూపండి.
సాధన:
అనంత స్పర్శరేఖల సమీకరణాలు

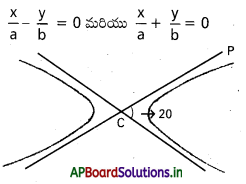
అనంత స్పర్శరేఖల మధ్యకోణము 2θ అయితే.
tan θ = \(\frac{b}{a}\) = అనంత స్పర్శరేఖ వాలు
θ = tan^-1 \(\left(\frac{b}{a}\right)\)
అనంత స్పర్శరేఖల మధ్యకోణము = 2θ = 2tan^-1 \(\left(\frac{b}{a}\right)\)
sec² θ = 1 + tan² θ = 1 + \(\)
= \(\frac{a^2+b^2}{a^2}=\frac{a^2 e^2}{a^2}\) = e²
sec θ = e ⇒ θ = sec^-1e
అనంత స్పర్శరేఖల మధ్యకోణము
= 2tan^-1 \(\left(\frac{b}{a}\right)\) లేదా 2 sec^-1 (e)