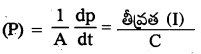AP Inter 2nd Year Physics Notes Chapter 11 విద్యుదయస్కాంత తరంగాలు

Students can go through AP Inter 2nd Year Physics Notes 11th Lesson విద్యుదయస్కాంత తరంగాలు will help students in revising the entire concepts quickly.

AP Inter 2nd Year Physics Notes 11th Lesson విద్యుదయస్కాంత తరంగాలు

→ విద్యుత్ వలయంలో కొంత భాగంలో కాలంతో పాటు విద్యుత్ ప్రవాహంలో మార్పురేటు వల్ల జనించే విద్యుత్ను స్థానభ్రంశ విద్యుత్ ప్రవాహం అంటారు.

→ విద్యుదయస్కాంత తరంగాలలో విద్యుత్ మరియు అయస్కాంతక్షేత్రాలు పరస్పరం లంబంగా కాలంతో మారుతూ తరంగ ప్రసార దిశకు పరస్పరం లంబంగా ఉంటాయి.

→ విద్యుదయస్కాంత తరంగాలను సైద్ధాంతికంగా మాక్స్వెల్ గుర్తించాడు.

→ ఆంపియర్ వలయనియమాన్ని మాక్స్వెల్ సవరించాడు.

→ మాక్స్వెల్ సమీకరణాలు స్థిరవిద్యుత్ గాస్ నియమం, అయస్కాంతత్వములో గాన్ నియమం, విద్యుదయస్కాంత ప్రేరణలో ఫారడే నియమం మరియు ఆంపియర్ వలయనియమం.

→ హెర్ట్ మరియు కొందరు సైంటిస్టులు ప్రయోగ పూర్వకంగా విద్యుదయస్కాంత తరంగాలను ఉత్పత్తి చేసి, అధ్యయనం చేశారు.

→ విద్యుదయస్కాంత తరంగాలు తిర్యక్ స్వభావాన్ని కలిగి ఉంటాయి.

→ విద్యుదయస్కాంత తరంగాల వేగం, కాంతి వేగానికి సమానం.

→ త్వరణం చెందే ఆవేశాలు విద్యుదయస్కాంత తరంగాలను జనింపజేస్తాయి.

→ విద్యుదయస్కాంత తరంగాల పౌనఃపున్యము (లేదా) తరంగదైర్ఘ్య మొత్తం అవధిని విద్యుదయస్కాంత వర్ణపటం అంటారు.

→ స్థానభ్రంశ విద్యుత్ (i_D) = ε₀\(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\)

→ ఆంపియర్ వలయ నియమం, \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \ell\) = μ₀(i₀ + ε₀ \(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\))

→ మాక్స్వెల్ సమీకరణాలు

• \(\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}\) = q/ε₀ (స్థిరవిద్యుత్ గాస్ నియమం.)
• \(\oint \vec{B} \cdot \overrightarrow{d s}\) = 0 (అయస్కాంతత్వములో గాస్ నియమం.)
• \(\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d} \ell}=\frac{-\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) (విద్యుదయస్కాంత ప్రేరణలో ఫారడే నియమం.)
• \(\int \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{d} \ell}\) = μ₀ (i₀ + ε₀\(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\))

→ కాంతి వేగము (C) = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\) = 3 × 10⁸ m/s

→ వక్రీభవన గుణకం (μ) = \(\frac{\mathrm{C}}{\mathrm{V}}=\sqrt{\frac{\mathrm{i} \varepsilon}{\mathrm{i}_0 \varepsilon_0}}\)

→ విద్యుత్ క్షేత్రం యొక్క శక్తి సాంద్రత (U_E) = \(\frac{1}{2}\)ε₀E²

→ అయస్కాంతక్షేత్రం యొక్క శక్తి సాంద్రత (U_B) = \(\frac{\mathrm{B}^2}{2 \mu_0^2}\)

→ పాయింటింగ్ సదిశ \((\overrightarrow{\mathrm{P}})=\frac{1}{\mu_0}(\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}})\)

→ విద్యుదయస్కాంత తరంగాల తీవ్రత (I) = \(\frac{1}{2}\)ε₀CE₀²

→ పీడనం (P)